🧕🏽 💎 🚳 Hampir saluran MIMO termudah dengan fading (termasuk model Kronecker) 👩🏻 ⛵️ 🧝🏽

Hari baik untuk semua!

Mempertimbangkan topik keragaman spasial , kami telah menyentuh kedua isu memudar dalam saluran komunikasi dan mengapa memudar tersebut terjadi. Hari ini saya mengusulkan untuk membicarakan topik ini dengan sedikit lebih detail.

Selain itu, dalam artikel hari ini kita akan sedikit menyentuh masalah korelasi spasial saluran MIMO, yang secara tradisional dibahas dalam kursus kursus Komunikasi Seluler ( CSP ) Profesor Haardt , dan oleh karena itu, menurut pendapat saya, publikasi seperti itu tidak akan berlebihan. Dan, saya perhatikan segera, berbagai masalah tidak terbatas hanya digunakan dalam komunikasi seluler.

Secara umum, saya mengundang semua yang tertarik pada subjek komunikasi nirkabel untuk membaca, dan mari kita pergi!

Colin Slater "Memori memudar" . Ya, untuk mengurangi segalanya menjadi satu topik mungkin berlebihan, tetapi dengan metafora semacam itu, saya pikir Anda dapat membayangkan apa yang penerima terima setelah semua jenis pengaruh pada sinyal informasi asli ...

Apa yang kita bicarakan

Mari kita mulai dengan fakta bahwa di alam ada apa yang disebut suara multiplikasi yang mempengaruhi daya sinyal yang diterima - memudar .

Istilahnya, seperti yang sudah Anda duga, tidak langsung diterjemahkan dalam bahasa Rusia dan Inggris, tetapi ini tidak terlalu penting.

Dalam sastra Inggris, istilah fading menyiratkan pengaruh tertentu, yang, seolah-olah, menyebabkan sinyal kita memudar, untuk "memudar."

Dalam literatur kami, istilah fading biasanya digunakan, dan ini terutama disebabkan oleh efek multipath: jika gelombang elektromagnetik menemukan salinannya yang dihasilkan oleh refleksi dan difraksi, dan mereka berada dalam antifase, gelombang akan membatalkan satu sama lain - yaitu, saluran , seolah-olah, membeku .

Fading cepat dan lambat ( fast and slow fading).

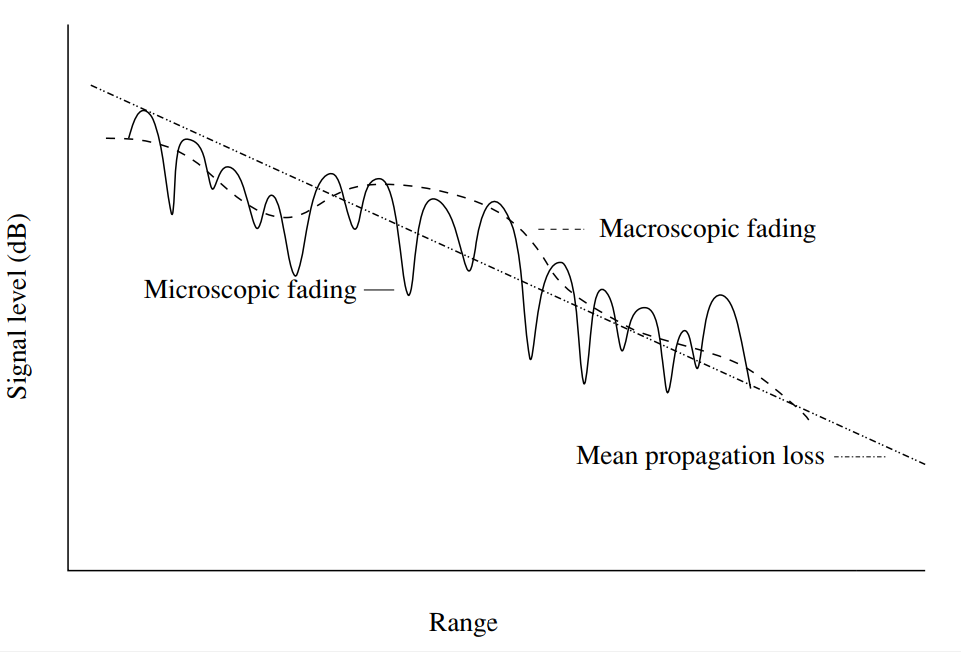
Fig. 1. Fluktuasi daya sinyal di saluran nirkabel tergantung pada jarak. Tingkat rata-rata kehilangan propagasi meningkat secara monoton dengan meningkatnya rentang. Penyimpangan lokal dapat terjadi karena memudar makroskopis (lambat) dan mikroskopis (cepat) [1, hal.14].

Saya akui segera, hari ini kita tidak akan bekerja dengan memudar lambat, tetapi kita akan berbicara tentang yang cepat dengan cukup detail.

Fig. 2. Ilustrasi efek naungan: sebagai aturan, fading lambat terjadi karena naungan (bayangan). Untuk simulasi, distribusi lognormal biasanya dipilih.

Jika Anda ingin membaca sedikit tentang slow fading, khususnya, dan tentang bagaimana Anda dapat mensimulasikan saluran satelit, secara umum, saya mengundang Anda ke sini !

Cepat memudar

Fading cepat terjadi, sebagai suatu peraturan, karena dua alasan utama:

karena propagasi multipath yang telah kami sebutkan dan / atau
karena pergeseran frekuensi Doppler .

Yang terakhir ini sangat terlihat untuk sistem satelit , tetapi mereka tidak selalu diperhitungkan untuk kasus komunikasi terestrial karena fakta bahwa stasiun pangkalan dalam kasus ini biasanya stasioner.

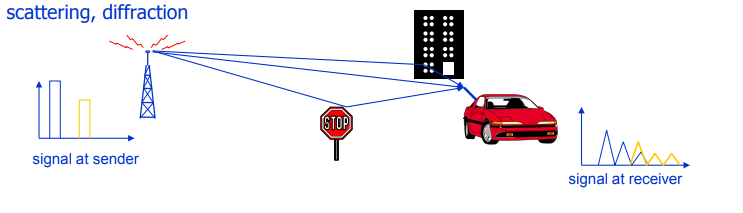
Fig. 3. Ilustrasi penyebab fading. Perhatian khusus diberikan pada penyebaran dan difraksi: justru karena fenomena inilah yang disebut propagasi multipath terbentuk, yang mengarah ke interferensi simbolik ( ISI ).

Tapi itu jauh dari semua.

Fading selektif vs. Datar memudar

Di atas, kami membagi gangguan kami dengan sifat kejadiannya . Namun, gangguan juga dapat dibagi berdasarkan sifat dari efek pada sinyal yang ditransmisikan . Dan di sini kita membutuhkan konsep selektivitas saluran.

Kami memberikan klasifikasi kecil sesuai dengan [1, hlm. 14-18]. Jadi, memudar cepat dapat:

Selektif
a. Frekuensi selektif
b. Selektif waktu
c. Selektif spasial (ini terkait dengan masalah sudut kedatangan dan keberangkatan gelombang EM - hari ini kami tidak akan menganalisis masalah ini)
Flat - lebih condong ke arah sifat memudar lambat (ya, ini adalah paradoks)

Apa yang termaksud oleh istilah terakhir dijelaskan dari kebalikannya.

Pertama, jika lebar spektrum sinyal yang dikirimkan oleh kami melebihi bandwidth saluran yang koheren , maka mereka mengatakan bahwa kami berurusan dengan interferensi selektif frekuensi.

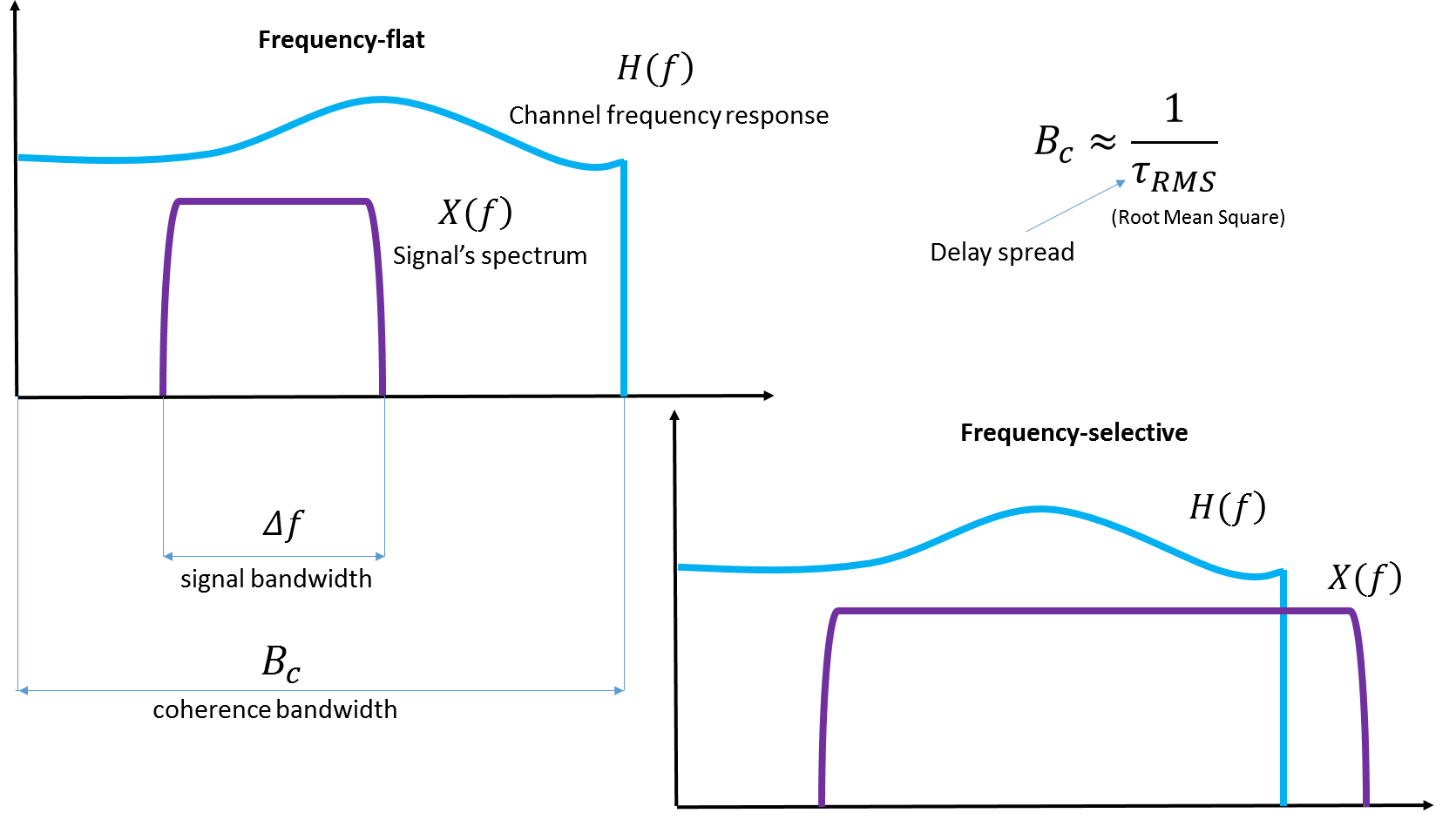
Fig. 4. Ilustrasi bandwidth yang koheren. Saya pikir itu bukan ide yang buruk untuk melampirkan ilustrasi dari Wiki , jika dia sendiri menambahkannya di sana.

Perhatikan variabel Delay spread - penyebaran keterlambatan. Ini adalah penyebaran dalam penundaan antara kedatangan salinan berbeda dari sinyal yang sama yang diukur ketika karakteristik saluran nyata tertentu ditentukan.

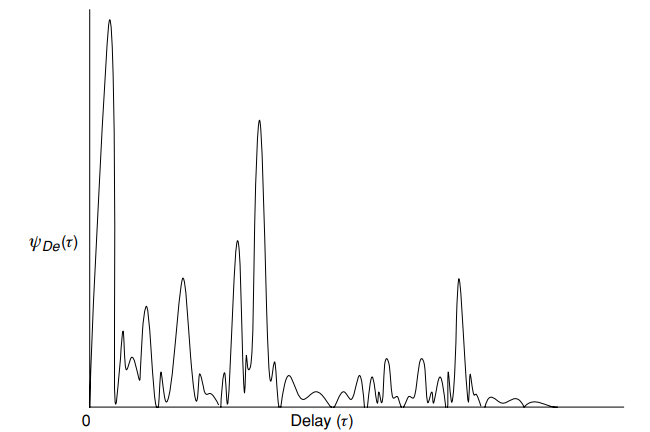
Fig. 5. Profil keterlambatan (daya) yang khas $\ psi_ {De} (\ tau)$ - Daya rata-rata sebagai fungsi penundaan $\ tau$ . [1, hlm. 16]

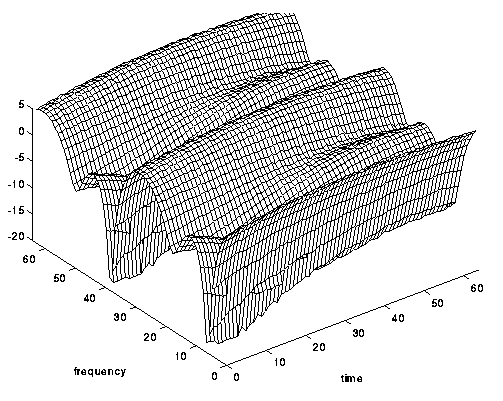
Fig. 6. Frekuensi-selektif, tetapi bukan saluran selektif-waktu .

Untuk setiap rentang, pita koheren akan berbeda.

Misalnya, untuk S-band (saya tertarik ketika saya mencari informasi tentang sistem satelit) Bc = 0,5 - 2 MHz (Kanatas AG, Panagopoulos AD (ed.). Propagasi Gelombang Radio dan Pemodelan Saluran untuk Bumi - Sistem Angkasa. - CRC Press, 2016 - hal. 107).

Ini sangat cocok pada kecepatan baud , misalnya, transceiver satelit seperti itu . Dan tidak ada yang mengejutkan: laju simbol jenis linear modulasi digital (PSK, QAM, OFDM) bertepatan dengan pita yang ditempati oleh sinyal (lihat Goldsmith A. Wireless communication . - Stanford University, 2004. - hal. 140, 326), yang berarti alangkah baiknya untuk mencoba memencet sinyalnya ke dalam pita yang koheren. Frekuensi masih merupakan sumber daya yang berharga.

Kedua, jika panjang sinyal kami dalam domain waktu melebihi waktu koherensi saluran , maka mereka mengatakan bahwa kami berurusan dengan saluran yang bervariasi dalam waktu.

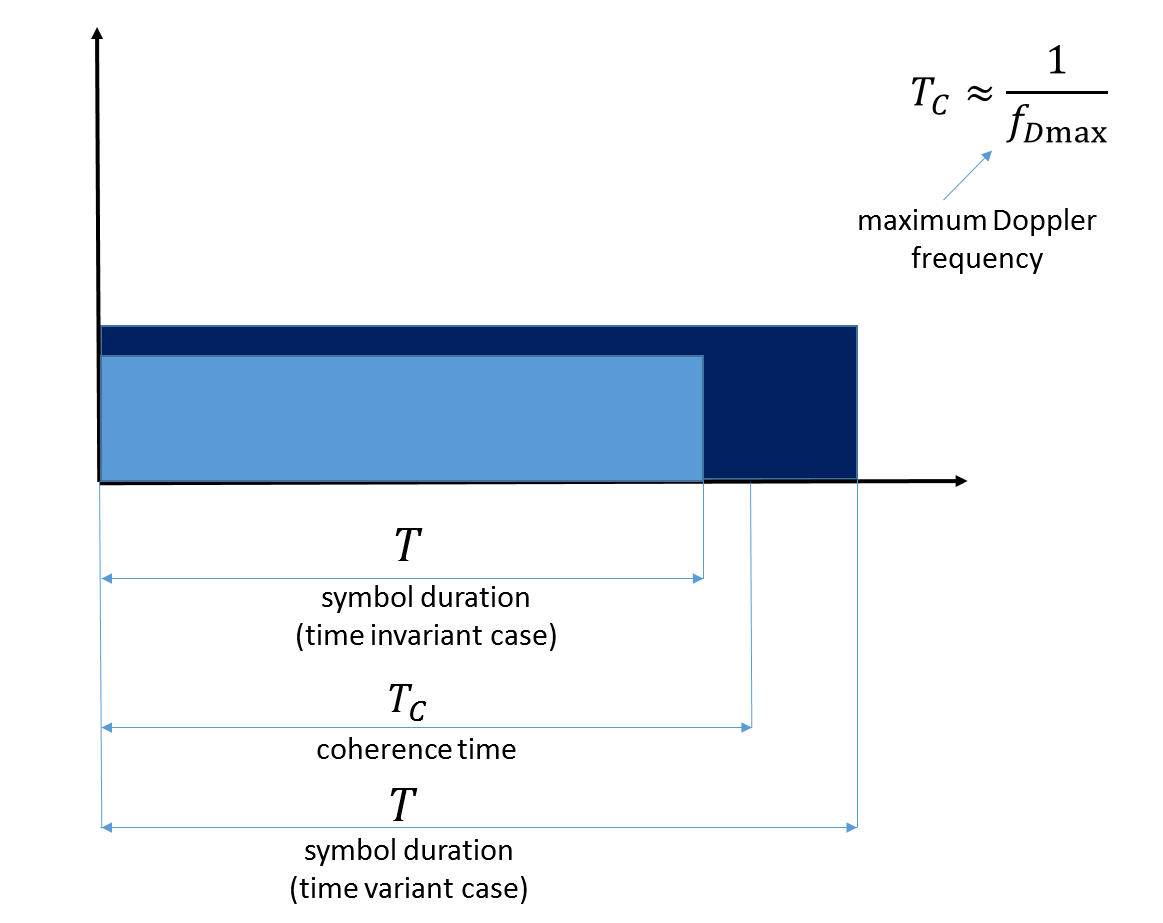
Fig. 7. Ilustrasi waktu koherensi. Harap dicatat bahwa di sini frekuensi Doppler maksimum mencerminkan pergerakan terminal seluler itu sendiri.

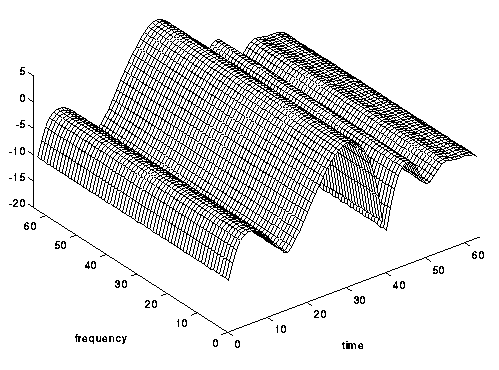
Fig. 8. Frekuensi hampir tidak selektif, tetapi selektif dalam waktu: saluran yang cepat membusuk.

Dalam kehidupan nyata, sayangnya, kita harus mengharapkan keduanya.

Saluran Rayleigh selektif waktu dan selektif frekuensi; "Situasi yang sebenarnya."

Sumber ilustrasi: Teknologi nirkabel Gigabit

Nah, dan karenanya, jika kita berhasil menghindari hal di atas, maka kita akan sampai pada kasus yang paling sederhana dan paling nyaman - flat fading [1, p. 14-18] [2, hlm. 88-92].

Saluran fading termudah

Anda mungkin telah melihat cara serupa untuk mensimulasikan saluran datar yang pudar di suatu tempat:

h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg))) % MatLab / Octave

Apa yang dimaksud:

kurangnya penglihatan (kasus yang dibenarkan untuk komunikasi terestrial)
narrowband channel (narrowband channel) - pas dengan band yang koheren
- Omong-omong, kami mempertimbangkan contoh saluran broadband dalam artikel ini (Gbr. 4).
tidak ada selektivitas frekuensi juga - masuk ke dalam waktu yang koheren
kurangnya pergeseran frekuensi shading dan Doppler

Artinya, ini dia secara langsung: saluran datar dengan fading . Untuk kasus tanpa saling berhadapan, saluran ini juga disebut Rayleigh .

Tuan Rayleigh

Dari mana datangnya model seperti itu?

Pertama, berbicara tentang sistem komunikasi modern, kemungkinan besar kita berarti bekerja dengan sinyal digital. Selain itu, kami juga bekerja paling mungkin dengan jenis modulasi quadrature ( I / Q ), yaitu, dengan sinyal yang kompleks.

Fig. 9. Konstelasi sinyal QPSK . Koordinat kutub, satuan lingkaran. Misalnya, simbol 11 akan sesuai dengan koordinat yang setara dengan sekitar 0,7 + 0,7i .

Adalah logis untuk mengasumsikan pengaruh gangguan pada komponen nyata dan imajiner. Selain itu, patut mengikuti Teorema Limit Sentral untuk juga mengasumsikan sifat Gaussian dari efek tersebut. Kami menulis rumus [1, hlm. 39]:

$Z = X + jY \ qquad (1)$

dimana $X \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ dan $Y \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ Variabel acak yang terdistribusi normal.

Paling sering, model dengan daya rata-rata dinormalisasi digunakan:

$var \ {Z \} = E \ {\ kiri | Z \ kanan | ^ 2 \} = 1 \ qquad (2)$

Dan itu artinya $Z \ sim \ mathcal {N} (0, \, 1)$ .

Jika kita mengasumsikan distorsi independen dari komponen amplop sinyal: baik dalam-fase ( I -Dalam-fase) dan quadrature ( Q - Quadrature), maka posisi nomor dimana simbol asli akan dikalikan (maka suara multiplikatif ), dalam koordinat polar dapat dihitung secara harfiah oleh teorema Pythagoras:

$Z = \ sqrt {\ hat {X} ^ 2 + \ hat {Y} ^ 2} \ qquad (3)$

dimana $\ hat {X} \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ dan $\ hat {Y} \ sim \ mathcal {N} (0, \, \ sigma ^ 2)$ - ini juga variabel acak yang berdistribusi normal. Untuk daya terukur $\ hat {X} \ sim \ mathcal {N} (0, \, 1)$ , $\ hat {Y} \ sim \ mathcal {N} (0, \, 1)$ .

Dan di sini kita memiliki formula proses Rayleigh ! [2, hlm. 78]

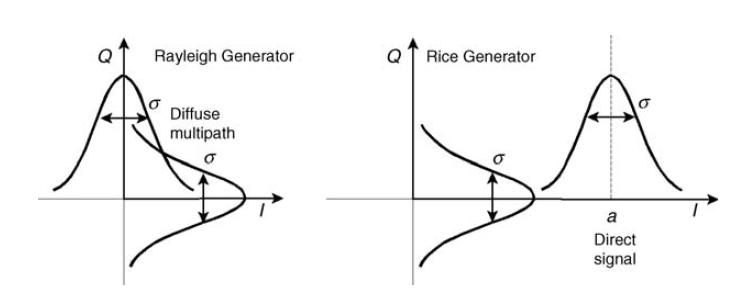
Fig. 10. Gaussian squared generator untuk memodelkan Rayleigh dan Rice fading [3, hal.125]. Kami akan berbicara tentang saluran Rice sedikit kemudian.

Penyimpangan liris.

Secara pribadi, saya sangat suka contoh penampakan senjata : jika dua senjata saling menembak dalam jumlah yang cukup banyak, maka untuk masing-masing individu distribusi hit akan normal, dan distribusi total hit adalah Rayleigh. Hal serupa terjadi dengan campur tangan kita.

Jika kita menganggap kasus paling sederhana tanpa korelasi spasial antara saluran (katakanlah kita memiliki beberapa saluran spasial - MIMO ), maka mereka mengatakan bahwa saluran tersebut putih spasial - putih spasial . Dan karena semua saluran independen, oleh karena itu, dimungkinkan untuk "menghasilkan" tidak hanya variabel acak yang didistribusikan menurut Rayleigh, tetapi juga vektor, matriks, dan tensor [3, hal. 125]:

$\ mathbf {H} _ {NLoS} = \ sqrt {\ frac {1} {2}} \ kiri (\ mathbf {G} _1 + j \ mathbf {G} _2 \ kanan) \ qquad (4)$

dimana $\ mathbf {G} _1 \ sim \ mathcal {N} (0, \, 1)$ dan $\ mathbf {G} _2 \ sim \ mathcal {N} (0, \, 1)$ Apakah matriks terdiri dari nilai yang terdistribusi normal.

Dari mana 1/2 berasal dari bawah root?

Semuanya cukup sederhana di sini: seperti yang kami katakan di atas, daya respons saluran harus sama dengan kesatuan, yaitu:

$P = E \ {hh ^ * \} = 1$

Untuk inilah faktor penskalaan diperkenalkan $\ sqrt {\ frac {1} {2}}$ .

Peragakan (ambil python untuk perubahan):

 import numpy as np N = int(1e6) h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N)) P = np.mean(h*np.conj(h)) print(np.round(P)) >>> (1+0j)

Untuk meringkas :
Komponen gangguan dengan tidak adanya visibilitas langsung dapat digambarkan sebagai vektor n-dimensi (tergantung pada dimensi saluran) independen yang terdistribusi secara identik ( IID - independent terdistribusi secara identik) sesuai dengan hukum Gaussian yang kompleks dengan simetri lingkaran dan nol tikar. angka ekspektasi ( ZMCSCG - nol-mean sirkular simetris kompleks Gaussian).

Twister seluruh lidah!

Hampir saluran fading termudah

Nah, bagaimana jika masih ada visibilitas langsung? Mungkin sudah ada model matematika yang sudah jadi pada skor ini?

Tentu ada! Sebagai contoh, ini [4] , digeneralisasi untuk kasus dengan beberapa antena penerima dan pemancar (MIMO):

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H_ {LoS}} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {H_ {NLoS} } \ qquad (5)$

dimana $$ \ mathbf {H}$ - ini sebenarnya adalah amplop kompleks dari respons impuls saluran (atau matriks saluran, jika kita berbicara tentang MIMO ), $$ \ mathbf {H_ {LoS}}$ Merupakan komponen visibilitas langsung (Line-of-Sight), dan $\ mathbf {H_ {NLoS}}$ - ini adalah komponen dari kurangnya visibilitas langsung (Non-Line-of-Sight), kami telah mempertimbangkannya.

Perhatikan variabel K - ini yang disebut faktor Padi (faktor Rician / Padi) - rasio kekuatan jalur perambatan langsung dengan daya semua jalur lainnya. Dialah yang menentukan seberapa banyak saluran kita akan mengalami gangguan.

Stephen O. "Steve" Rice

Term $\ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} = E \ {H \}$ mewakili ekspektasi matematis dari matriks saluran dan dapat dimodelkan berdasarkan geometri dari antena penerima dan pemancar antena:

$\ mathbf {H} _ {LoS} = \ mathbf {a} _R (\ theta_R) \ mathbf {a} _T (\ theta_T) ^ H \ qquad (6)$

dimana $\ mathbf {a} _R (\ theta_R)$ dan $\ mathbf {a} _T (\ theta_T)$ - ini adalah tanggapan dari antena penerima dan pemancar antena masing-masing, dan $\ theta_R$ dan $\ theta_T$ Apakah sudut kedatangan dan keberangkatan (sudut keberangkatan).

Faktor-faktor umumnya simetris dan dapat dijelaskan dengan rumus umum:

$\ mathbf {a} = \ kiri [1, e ^ {j2 \ pi d cos (\ theta)}, ..., e ^ {j2 \ pi d (N-1) cos (\ theta)} \ kanan] \ qquad (7)$

dimana $d$ Apakah jarak antara antena (jarak antena) dalam panjang gelombang, dan $N$ - ini adalah jumlah elemen dalam susunan antena (Gbr. 11).

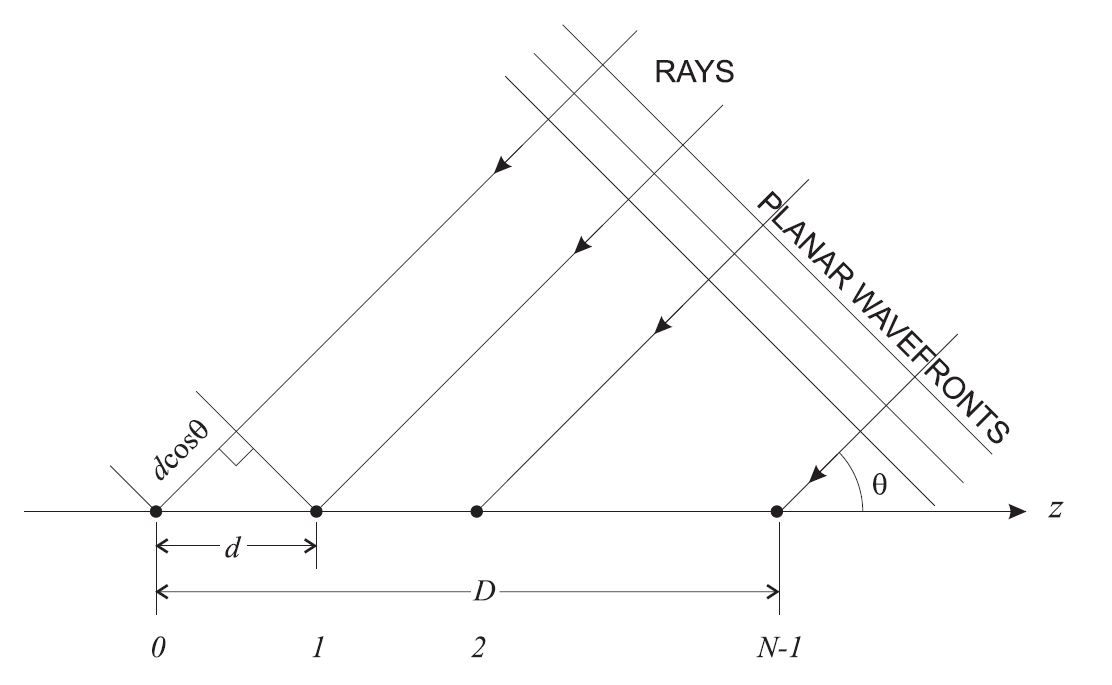
Fig. 11. Geometri dari array linier . Untuk Masimo MIMO, geometri, tentu saja, akan berbeda. Anda dapat membaca lebih lanjut tentang ini, misalnya, di sini .

Nah, sekarang model itu setidaknya agak dibongkar, Anda dapat menyederhanakannya.

Untuk kasus SISO (paling sederhana dan paling dasar), rumus (5) akan berbentuk:

$h = \ sqrt {\ frac {K} {K + 1}} + \ sqrt {\ frac {1} {2 (K + 1)}} \ kiri (G_1 + jG_2 \ kanan) \ qquad (8)$

untuk untuk 1 pemancar dan 1 antena penerima $\ mathbf {a} _T (\ theta_T) \ mathbf {a} _R (\ theta_R) = 1$ .

Dan ini, omong-omong, cocok dengan model pada Gambar 12.

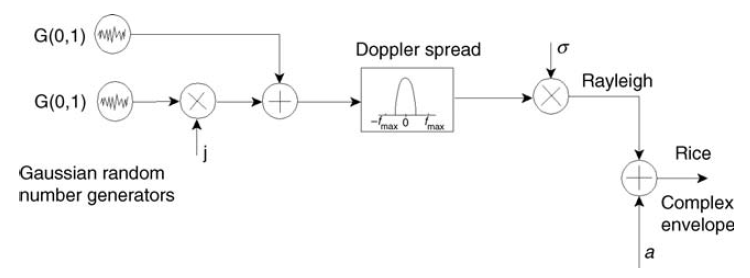
skema

Fig. 12. Skema pembentukan saluran Padi (sinyal pita sempit) [3, hal.127]. Di $K \ hingga 0$ saluran akan semakin merosot menjadi Rayleigh. Itu sebabnya saya menggunakan kata itu hampir dalam subtitle: saluran Rayleigh adalah kasus khusus dari saluran Rice. Ini juga terlihat dari rumus (5).

Mari kita jelaskan: $\ sigma = \ sqrt {\ frac {1} {2 (K + 1)}}$ Apakah parameter skala Rician, dan $a = \ sqrt {\ frac {K} {K + 1}}$ Merupakan parameter noncentrality.

Jika kita mempertimbangkan flat fading, diasumsikan bahwa blok Doppler Spread memiliki respons 1.

Secara umum, untuk tujuan pemodelan Doppler Spread, kemungkinan besar Anda akan menemukan model Jakes (bentuk-U) berdasarkan Teknik Sum-of-sinusoids . Secara teoritis, spektrum model seperti itu terlihat seperti ini:

Kepadatan spektral daya atenuasi Rayleigh dengan pergeseran Doppler maksimum 10 Hz. Sumber

Namun, dalam hidup, dinilai oleh [1, hal. 15] spektrum seperti itu masih terlihat kurang merata:

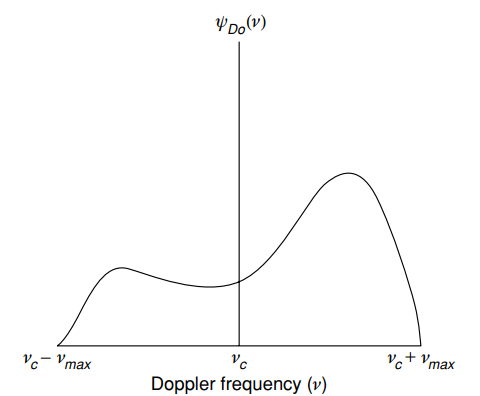
Spektrum Doppler (energi) yang khas $\ psi_ {Do} (v)$ - Daya rata-rata sebagai fungsi frekuensi Doppler $(v)$ [1, hlm. 15].

Harapan ... Realitas.

Ada skema seperti itu untuk menggabungkan dengan memudar lambat.

Misalnya, ini untuk model Corazza-Vatalaro (C & V) :

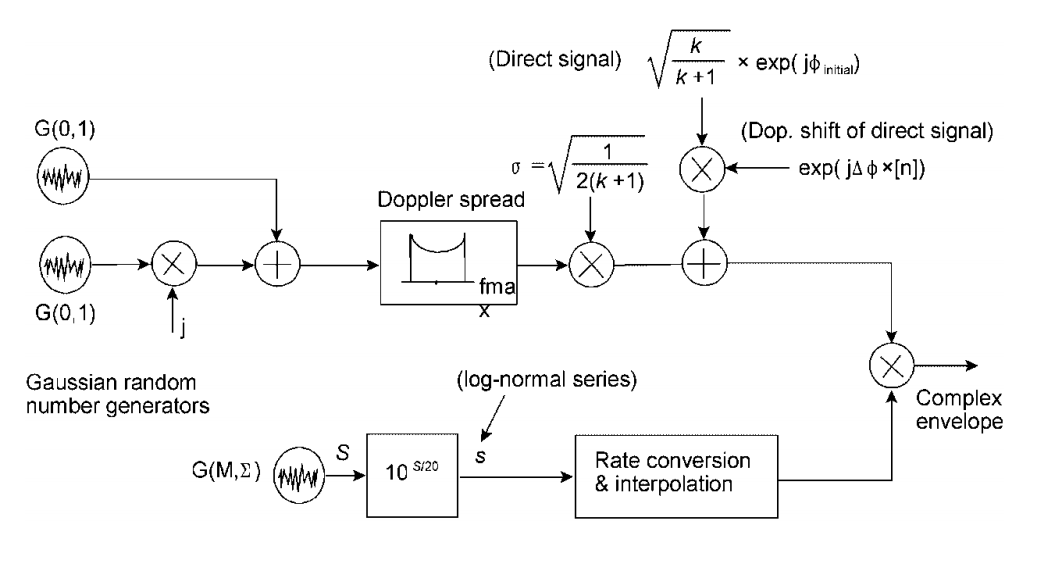
lihat Fontan, FP, Mayo, A., Marote, D., Prieto - Cerdeira, R., Mariño, P., Machado, F., & Riera, N. (2008). Tinjauan model generatif untuk saluran propagasi satelit mobile land narrowband. Jurnal Internasional Komunikasi dan Jaringan Satelit, 26 (4), 291-316.

Tapi ini adalah kisah yang sangat berbeda ...

Memodelkan saluran fading termudah di MatLab

Mari kita bandingkan perhitungan yang diterima dengan sesuatu yang sudah diperiksa. Misalnya, dengan fungsi MatLab khusus .

Untuk menguji model, untuk bagian kami, kami menghasilkan pesan biner acak (panjang pesan adalah 100.000 bit), memodulasi menggunakan M-PSK atau M-QAM , mengalikan elemen dengan elemen proses fading, menambahkan white Gaussian white, menyamakan equalizer Forcing Nol, mendemodulasi dan menghitung rasio kesalahan bit (BER - rasio kesalahan bit) (Gbr. 13). Jumlah tes akan sama dengan seratus.

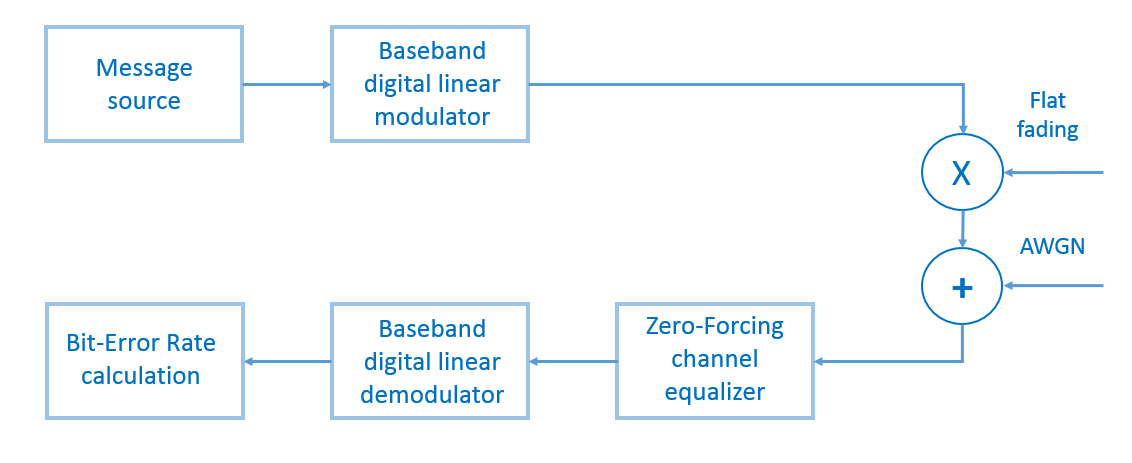
Gbr. 13. Diagram blok dari model sistem transmisi yang akan dijelaskan skrip kami.

Script dapat dilihat di sini.

Dan unduh di sini .

 clear all; close all; clc EbNo = 0:40; K = [4.0; 0.6]; M = [4; 8; 16; 64; 256]; %Positions of modulation (M-PSK or M-QAM) for k = 1:length(K) for m = 1:length(M) message = randi([0, M(m)-1], 100000, 1); if M(m) >= 16 mod_msg = qammod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo,'qam',M(m),1,K(k)); else mod_msg = pskmod(message, M(m), pi/4, 'gray'); ric_ber(:, m, k) = berfading(EbNo, 'psk', M(m), 1, K(k)); end Es = mean(abs(mod_msg).^2); No = Es./((10.^(EbNo./10))*log2(M(m))); h = sqrt( K(k)/(K(k)+1)) +... sqrt( 1/(K(k)+1))*(1/sqrt(2))*(randn(size(mod_msg))... + 1j*randn(size(mod_msg))); ric_msg = mod_msg.*h; % Rician flat fading for c = 1:100 for jj = 1:length(EbNo) noisy_mod = ric_msg +... sqrt(No(jj)/2)*(randn(size(mod_msg))+... 1j*randn(size(mod_msg))); %AWGN noisy_mod = noisy_mod ./ h; % zero-forcing equalization if M(m) >= 16 demod_msg = qamdemod(noisy_mod, M(m), pi/4, 'gray'); else demod_msg = pskdemod(noisy_mod, M(m), pi/4, 'gray'); end [number,BER(c,jj)] = biterr(message,demod_msg); end end sum_BER(:,m, k) = sum(BER)./c; end end figure(1) semilogy(EbNo, sum_BER(:,1,1), 'b-o', EbNo, sum_BER(:,2,1), 'r-o',... EbNo, sum_BER(:,3,1), 'g-o', EbNo, sum_BER(:,4,1), 'c-o',... EbNo, sum_BER(:,5,1), 'k-o',... EbNo, ric_ber(:,1,1), 'b-', EbNo, ric_ber(:,2,1), 'r-',... EbNo, ric_ber(:,3,1), 'g-', EbNo, ric_ber(:,4,1), 'c-',... EbNo, ric_ber(:,5,1), 'k-', 'LineWidth', 1.5) title('Rician model (K = 4.0)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)', '16-QAM(theory)',... '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on figure(2) semilogy(EbNo, sum_BER(:,1,2), 'b-o', EbNo, sum_BER(:,2,2), 'r-o',... EbNo, sum_BER(:,3,2), 'g-o', EbNo, sum_BER(:,4,2), 'c-o',... EbNo, sum_BER(:,5,2), 'k-o',... EbNo, ric_ber(:,1,2), 'b-', EbNo, ric_ber(:,2,2), 'r-',... EbNo, ric_ber(:,3,2), 'g-', EbNo,ric_ber(:,4,2), 'c-',... EbNo, ric_ber(:,5,2), 'k-','LineWidth', 1.5) title('Rician model (K = 0.6)') legend('QPSK(simulated)', '8-PSK(simulated)',... '16-QAM(simulated)', '64-QAM(simulated)' ,'256-QAM(simulated)',... 'QPSK(theory)','8-PSK(theory)',... '16-QAM(theory)', '64-QAM(theory)' ,'256-QAM(theory)','location','best') xlabel('EbNo (dB)') ylabel('BER') grid on

Anda harus mendapatkan sesuatu seperti ini:

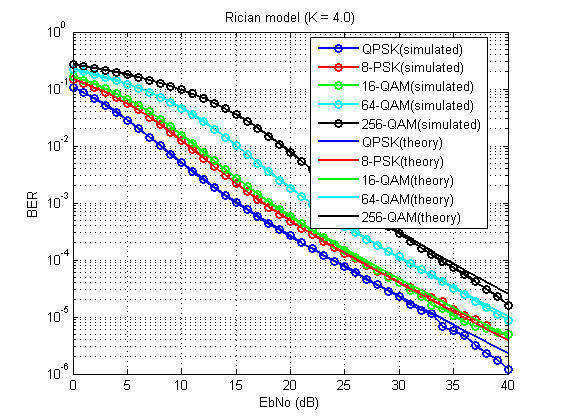
Fig. 14. Koefisien kesalahan bit untuk model yang dipertimbangkan (K = 4.0).

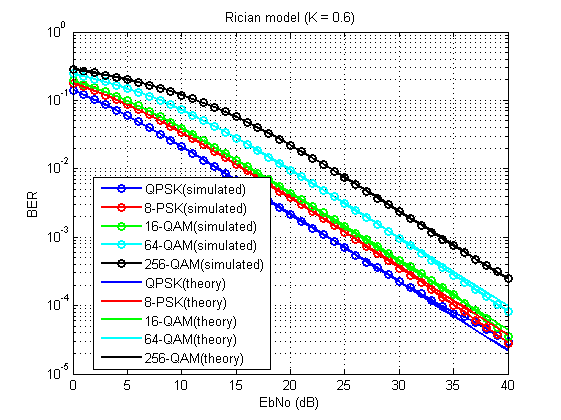
Fig. 15. Tingkat kesalahan bit untuk model yang dipertimbangkan (K = 0,6).

Bukan tanpa cacat, tentu saja (karena jumlah rata-rata yang terbatas), tetapi secara umum, dapat dilihat bahwa itu berfungsi!

Oke, tapi apakah mungkin untuk skala percobaan ke kasus MIMO? Ya tentu saja

Untuk melakukan ini, kami membuat satu asumsi: matriks saluran akan terdiri dari jalur propagasi independen, yang masing-masing akan didistribusikan sesuai dengan Rice.

Dalam kondisi apa ini memungkinkan?

Seperti yang kami sebutkan di atas, komponen IID dapat dihasilkan dalam dimensi apa pun. Ini berarti bahwa setiap saluran MIMO putih spasial tanpa saling berhadapan dapat dimodelkan sebagai satu set saluran SISO (tergantung pada dimensi saluran).

Dengan komponen garis pandang yang sedikit lebih rumit - Anda perlu memperhitungkan posisi kisi-kisi.

Pertimbangkan formula (5): jika matriks kita dari komponen garis pandang hanya akan terdiri dari unit $\ mathbf {H} _ {LoS} = \ mathbf {1}$ , tampaknya komponen Raysov juga menjadi putih spasial.

Untuk mendekati ini, kami menuliskan komponen line of sight secara lebih rinci daripada dalam rumus (6):

$\ mathbf {H} _ {LoS} = \ begin {bmatrix} 1 \\ \ exp (j2 \ pi dcos (\ theta_R)) \\. \\. \\. \\ \ exp (j (M_R-1) 2 \ pi dcos (\ theta_R)) \ end {bmatrix} \ begin {bmatrix} 1 & \ exp (j2 \ pi dcos (\ theta_T)) &. &. &. & \ exp (j (M_T-1) 2 \ pi dcos (\ theta_T)) \ end {bmatrix}$

Sangat mengejutkan bahwa jika $\ theta_R = \ theta_T = 90 ^ o$ , maka matriks akan terdiri dari satu unit. Secara geometris, ini adalah situasi ketika dua array elemen diorientasikan secara ketat satu sama lain:

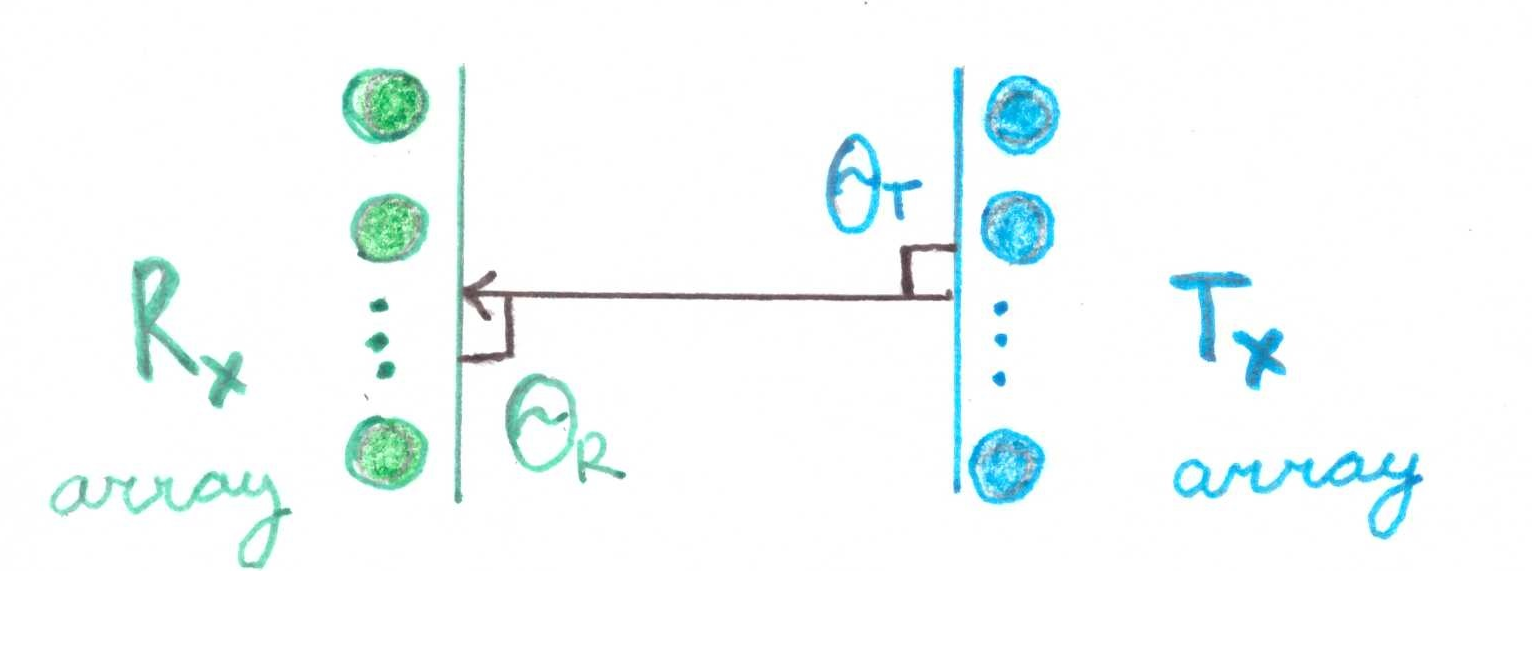
Mari kita lakukan demonstrasi matematika kecil:

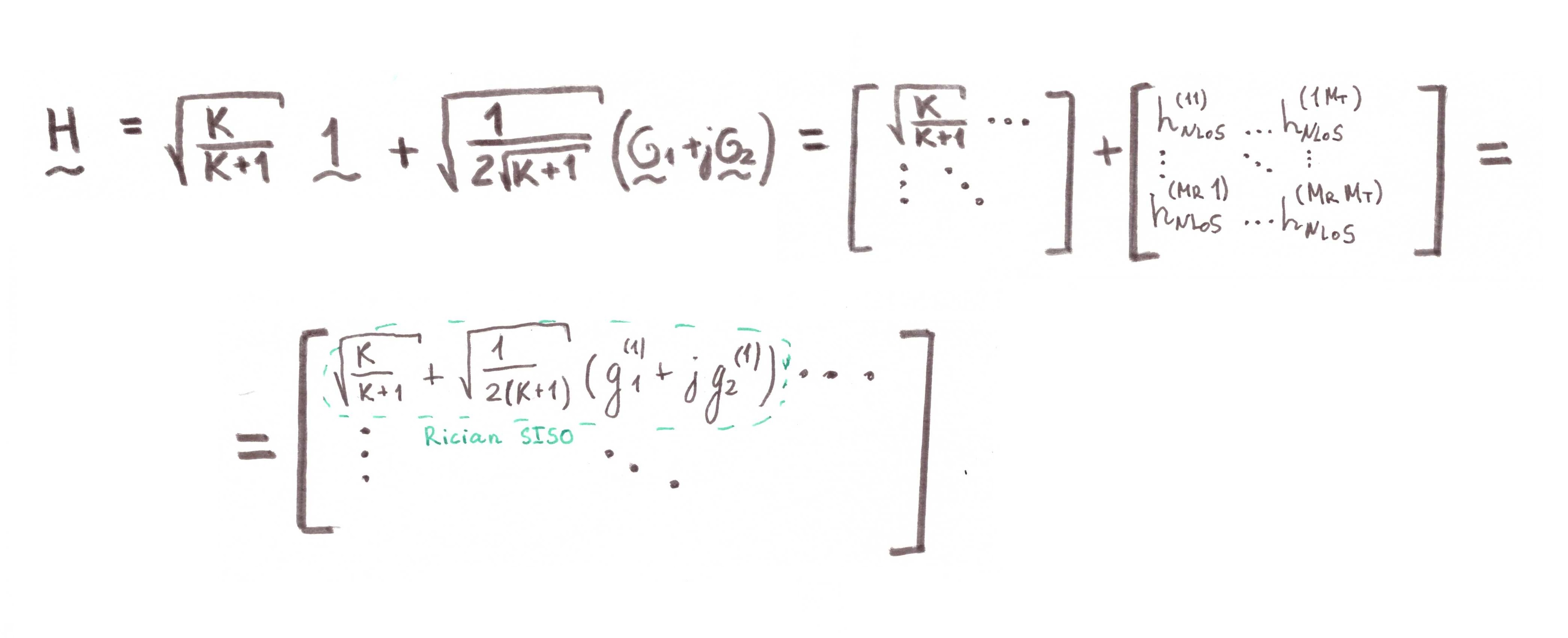
Untuk pemodelan, kami menggunakan skema Alamouti sebagai basis. Seharusnya menghasilkan sesuatu seperti ini:

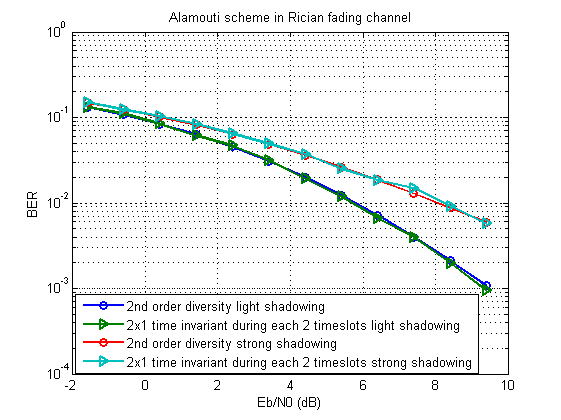
Skrip yang diperluas dapat diunduh di sini .

Bagus sekali.

Hampir saluran fading dan korelasi spasial termudah

Dan sekarang, menyelesaikan perjalanan kita ke dunia perhitungan statistik, mari kita sedikit lebih dekat dengan kenyataan.

Di atas, kami mempertimbangkan kasus ketika komponen dari kurangnya garis penglihatan secara spasial putih . Namun, dari sistem nyata kita masih harus mengharapkan beberapa korelasi antara antena, dan karena itu antara jalur propagasi gelombang EM.

Kami memperkenalkan variabel baru - matriks korelasi spasial:

$\ mathbf {R} = E \ {vec (\ mathbf {H}) vec (\ mathbf {H}) ^ H \} \ qquad (8)$

di mana vec menunjukkan operasi vektorisasi . By the way, matriks ini hanya akan mempengaruhi komponen dari kurangnya garis pandang , dan karenanya dalam hal ini $\ mathbf {H} = \ mathbf {H} _ {NLoS}$ .

Contoh untuk MIMO 2x2

Masuk akal untuk mengasumsikan bahwa dalam kehidupan nyata, matriks ini pertama-tama ditentukan melalui pengukuran, dan baru kemudian mereka digunakan untuk pemodelan:

$vec (\ mathbf {H} _ {NLoS}) = \ mathbf {R} ^ {1/2} vec (\ mathbf {H} _w) \ qquad (9)$

dimana $\ mathbf {H} _w$ Apakah matriks IID ( w berarti spasial w ).

Perhatikan bahwa menaikkan matriks ke daya bukan peningkatan ke kekuatan masing-masing elemennya. Oleh karena itu, dalam kasus kami, fungsi sqrt () tidak dapat digunakan di MatLab . Gunakan operator ^ .
Dalam kasus Python, Anda tidak dapat menggunakan operator eksponensial ** dan metode sqrt dari modul numpy yang populer. Anda perlu menggunakan metode fractional_matrix_power dari modul scipy .

Jika penerima dan pemancar cukup independen satu sama lain, seperti pada Gambar 16, maka model Kronecker dapat diterapkan [1, hal. 40], untuk mengurangi jumlah koefisien untuk perhitungan:

$\ mathbf {R} = \ mathbf {R} ^ T_T \ otimes \ mathbf {R} _R \ qquad (10)$

dimana $\ otimes$ menunjukkan sebuah karya Kronecker .

Leopold Kronecker

Kami secara terpisah mempertimbangkan komponen-komponen dari matriks ekspresi:

$\ mathbf {R} _R = \ frac {1} {M_T} E \ kiri \ {\ kiri (\ mathbf {H} _ {NLoS} \ mathbf {H} ^ H_ {NLoS} \ kanan) ^ T \ kanan \ }$ Apakah matriks korelasi antena penerima,

$\ mathbf {R} _T = \ frac {1} {M_R} E \ kiri \ {\ mathbf {H} ^ H_ {NLoS} \ mathbf {H} _ {NLoS} \ kanan \}$ Merupakan matriks korelasi antena pemancar

$M_R$ dan $M_T$ - ini adalah jumlah antena penerima dan pemancar masing-masing. Kedua matriks adalah matriks Hermitian semi-pasti positif. Apalagi jajaran matriksnya $\ mathbf {H} _ {NLoS}$ dibatasi oleh nilai $mnt (peringkat (\ mathbf {R} _T), peringkat (\ mathbf {R} _R))$ .

Fig. 16.
Model difuser dalam hal penerima dan pemancar yang tidak berkorelasi. Titik hijau berarti difuser, penerima dan pemancar berarti biru dan merah. Saya minta maaf atas kualitasnya, ini adalah tangkapan layar dari salah satu pekerjaan rumah TU Ilmenau.

Matriks saluran dalam hal ini dapat ditulis sebagai:

$\ mathbf {H} = \ sqrt {\ frac {K} {K + 1}} \ mathbf {H} _ {LoS} + \ sqrt {\ frac {1} {K + 1}} \ mathbf {R} ^ {1/2} _R \ mathbf {H} _ {w} \ kiri (\ mathbf {R} ^ {1/2} _T \ kanan) ^ H \ qquad (11)$

Namun, untuk situasi seperti, misalnya, pada Gambar 17, Anda masih harus menggunakan matriks korelasi penuh (lihat rumus (9)).

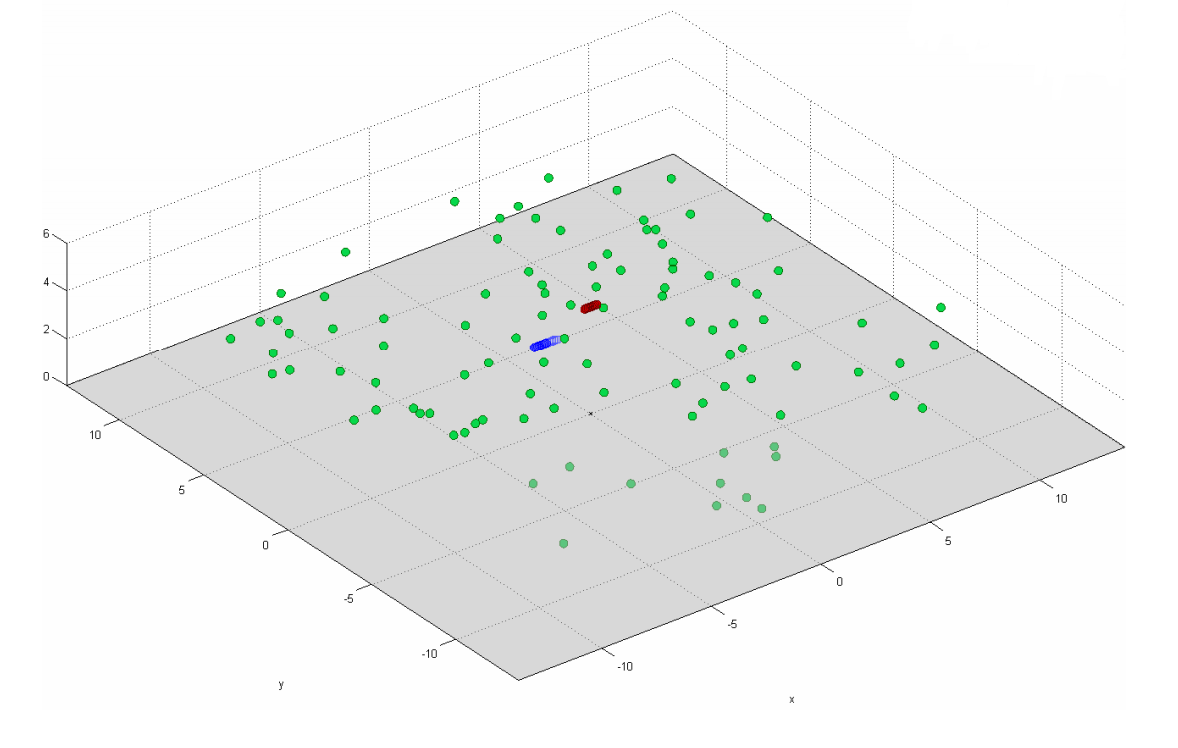
Fig. 17. Model diffuser dalam hal menghubungkan penerima dan pemancar. Titik hijau berarti difuser, penerima dan pemancar berarti biru dan merah.

Untuk mengkonsolidasikan apa yang telah kita pelajari dan melihat bagaimana korelasi spasial mempersulit kehidupan, mari kita coba menghitung bandwidth saluran. Misalnya, untuk MIMO 2x2.

Untuk melakukan ini, kami mengambil kasus-kasus berikut (yang kami maksudkan adalah flat fading yang sama, untuk kesederhanaan kami juga hanya mempertimbangkan saluran Rayleigh):

1) saluran putih spasial;
2) Model Kronecker dengan korelasi yang relatif lemah:

$\ mathbf {R} _T = \ mathbf {R} _R = \ begin {bmatrix} 1 & 0.4 \\ 0.4 & 1 \ end {bmatrix}$

3) Model Kronecker dengan korelasi yang relatif kuat:

$\ mathbf {R} _T = \ mathbf {R} _R = \ begin {bmatrix} 1 & 0,6 \\ 0,6 & 1 \ end {bmatrix}$

Kami akan menggunakan Python 3.4 di bagian ini. Fungsi untuk menghitung bandwidth akan diambil dari salah satu publikasi saya yang lalu .

 import numpy as np from numpy import linalg as LA import matplotlib.pyplot as plt from scipy.linalg import fractional_matrix_power def openloop_capacity(H_chan, SNR_dB): SNR = 10**(SNR_dB/10) Mt = np.shape(H_chan)[1] H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H) lambdas = LA.eigvals(H_sq) lambdas = np.sort(lambdas)[::-1] c = 0 for eig in lambdas: c = c + np.log2(1 + SNR*eig/Mt) return np.real(c)

Tentukan parameter utama sistem:

 Mr = 2 # number of receive antennas Mt = 2 # number of transmit antennas Rr1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rr2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rt1 = np.array([[1., .4], [.4, 1.]]) # case 1 Rt2 = np.array([[1., .6], [.6, 1.]]) # case 2 Rr1_half = fractional_matrix_power(Rr1, 0.5) Rr2_half = fractional_matrix_power(Rr2, 0.5) Rt1_half = fractional_matrix_power(Rt1, 0.5) Rt1_half_H = np.conj(Rt1_half).T Rt2_half = fractional_matrix_power(Rt2, 0.5) Rt2_half_H = np.conj(Rt2_half).T

Kami memulai simulasi:

 counter = 1000 SNR_dBs = [i for i in range(1, 21)] C_MIMO_uncorr = np.empty((len(SNR_dBs), counter)) C_MIMO_kron1 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron2 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron3 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron4 = np.empty((len(SNR_dBs), counter)) for c in range(counter): H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H)) H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H)) for idx, SNR_dB in enumerate(SNR_dBs): C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB) C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB) C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB) C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1) C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1) C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)

Menggambar

 plt.figure(figsize=(7, 5), dpi=100) plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated') plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1') plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2') plt.title("Rayleigh flat fading (MIMO 2x2)") plt.xlabel('SNR (dB)') plt.ylabel('Ergodic capacity (bps/Hz)') plt.legend() plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

Kami mendapatkan:

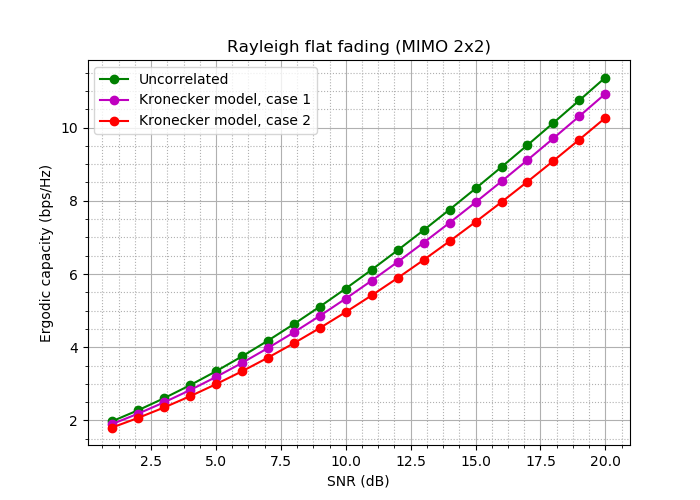
Fig. 18. Kurva bandwidth untuk percobaan ini.

Yah: bedanya, meskipun tidak kritis, adalah!

Kata penutup

Mungkin salah satu pembaca dapat memperhatikan bahwa hampir semua yang kita periksa hari ini (secara terperinci dan sepintas) sangat bergantung pada parameter dari objek matlab comm.MIMOChannel . Bagi saya, fakta ini sangat penting:

pertama, lebih lanjut mensistematisasikan hal di atas,
dan, kedua, ini menekankan bahwa kami menangani masalah saat ini.

Nah, dan sekarang, jika Anda menggunakan balok seperti itu, maka, saya harap, akan lebih jelas mengapa dan pena apa yang perlu Anda putar.

Terima kasih atas perhatian Anda!

Saya akan menambahkan di sini tautan ke slide tentang topik dari Reiner S. Thomä (Ilmenau), di mana ia memberi kami kuliah pada saat itu. Saya pikir seseorang akan berguna!

Sastra

Paulraj, Arogyaswami, Rohit Nabar, dan Dhananjay Gore. Pengantar komunikasi nirkabel ruang-waktu. Cambridge University Press, 2003.
Pandai Emas A. Komunikasi nirkabel. - Cambridge University Press, 2005.
Fontæn, Fernando Pærez, dan Perfecto Mariæo Espiæeira. Memodelkan saluran propagasi nirkabel: pendekatan simulasi dengan Matlab. Vol. 5. John Wiley & Sons, 2008.
Farrokhi, Farrokh R., et al. "Efisiensi spektral sistem nirkabel FDMA / TDMA dengan mengirim dan menerima array antena." Transaksi IEEE pada komunikasi nirkabel 1.4 (2002): 591-599.

Hampir saluran MIMO termudah dengan fading (termasuk model Kronecker)