Fraktal dalam bilangan irasional. Bagian 2

Bagian 0: Fraktal dalam bilangan prima.
Bagian 1: Fraktal dalam bilangan irasional.



Artikel ini berisi gambar Gif dan kontras. Epilepsi mungkin memiliki serangan epilepsi.

Dalam artikel sebelumnya, kami melihat algoritma visualisasi urutan biner. Mari kita ingat.

Ambil urutan biner. Sebagai contoh, beberapa bit pertama dari urutan fraktal yang dibahas dalam artikel sebelumnya:

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

0100110110010011001001101100

Kami menggambar bidang sel persegi. Kami mengatur bit di batas atas. Jarak antara bit adalah dua sel:



Untuk setiap bit, gambarkan jalur putus-putus di sepanjang diagonal (melalui sel). Untuk nol, gambar stroke pertama ke kanan:



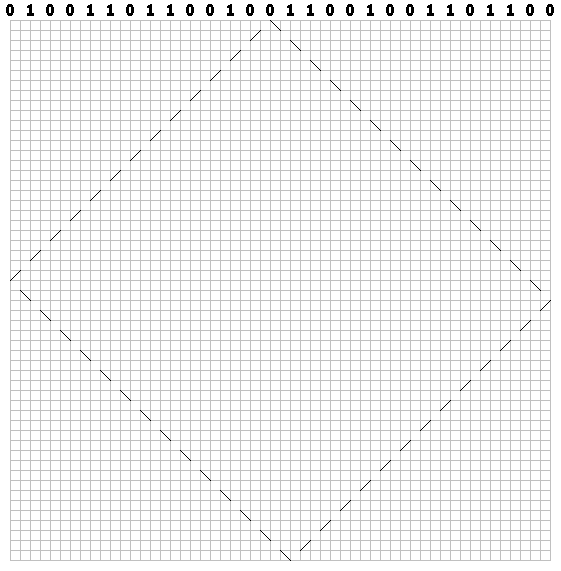
Untuk unit - ke kiri:



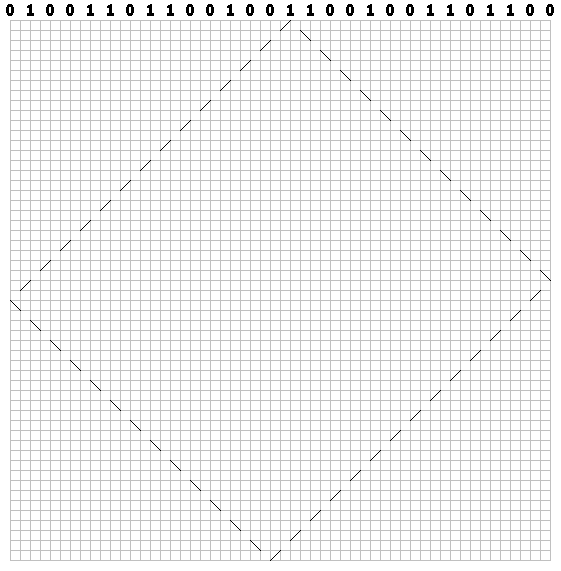
Gambar lintasan untuk setiap bit. Kami mendapat pola "biliar":



Pola yang identik (tanpa cacat di sepanjang diagonal - urutannya tidak terbatas, kami memvisualisasikannya sebagai urutan akhir) dapat diperoleh dengan cara lain. Balikkan setiap bit genap dalam urutan:

0 0 0 1 1 0 0 0 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 1 0 0 1

Selanjutnya, untuk setiap bit, gambar garis putus-putus vertikal:



Kami mengatur bit di sebelah kiri, menggambar garis horizontal:



Kami menggabungkan:



Setelah menulis artikel pertama, dua pertanyaan tetap tidak terselesaikan:

1. Apakah mungkin untuk menggambar pola fraktal untuk bilangan irasional. Kamu bisa. Masalah ini telah diatasi dalam artikel sebelumnya. Pada gambar di atas - bagian dari pola fraktal untuk $$$\ sqrt {2}$ . Jika Anda memilih salah satu kurva dalam pola ini:



Dapatkan kurva fraktal yang terkenal - “Fibonacci word fractal”.

2. Pertanyaan kedua adalah apakah mungkin untuk menulis suatu algoritma yang menggambarkan suatu pola:



Masalah kedua akan dibahas dalam artikel ini. Kami akan mewarnai pola dengan bantuan alat tenun, yang karyanya kami simulasikan menggunakan JavaScript.



Dalam diagram di atas - mesin termudah. Ini terdiri dari dua bingkai di mana benang diregangkan. Bingkai terhubung ke pedal. Ketika Anda menekan salah satu pedal, salah satu bingkai naik. Benang yang ditarik melalui bingkai ini naik dan benang melintang ditarik ke dalam celah yang dihasilkan antara benang. Jika Anda merentangkan benang genap dan ganjil melalui bingkai yang berbeda, Anda mendapatkan tenunan dalam pola kotak-kotak:



Pada mesin yang lebih kompleks, empat atau lebih frame digunakan:


Ashford 4 Shaft Table Loom

Agar tidak bingung pedal mana yang harus ditekan, mereka membuat diagram.



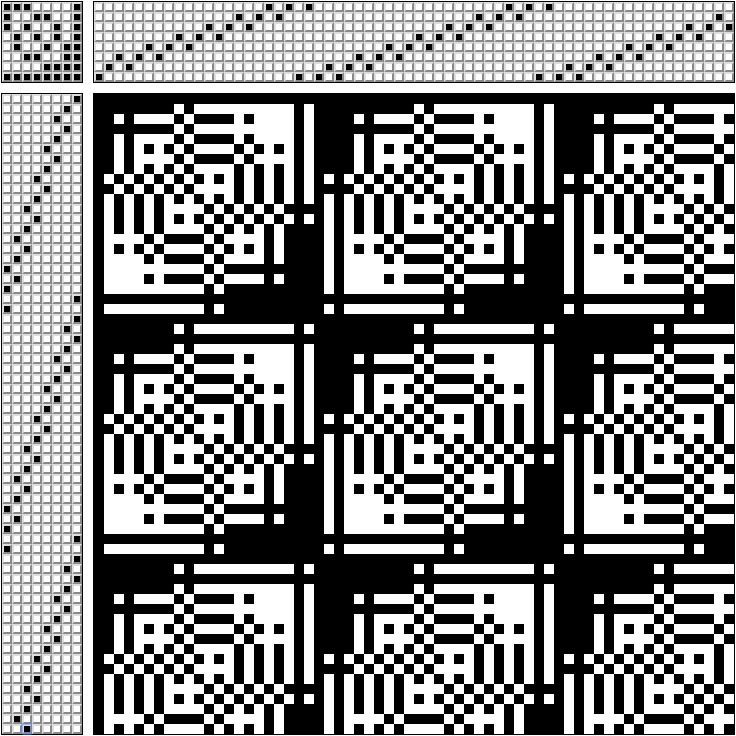
Di bagian kanan atas pola itu ditunjukkan melalui bingkai mana benang pergi (pola untuk alat tenun 8-frame).

Di sudut kiri atas - pedal yang menjepit pada saat yang sama (setiap pedal terhubung hanya dengan bingkainya sendiri).

Di bagian kiri bawah - dalam urutan apa untuk mengayuh.

Di bagian kanan bawah - apa yang kita dapatkan menenun. Jika Anda meregangkan benang putih melalui hitam - kita mendapatkan pola monokrom.

Segera "masukkan" prinsipnya mungkin tampak sedikit sulit. Gambar di bawah ini menunjukkan bagaimana pola tenun terbentuk:



Mari kita menulis naskah. Kami akan meregangkan utas melalui bingkai menggunakan array array satu dimensi2. Dalam array array satu dimensi1, kita menulis urutan pedal clamping. Dalam array3 (8x8 binary array) kita menulis pedal mana yang harus dijepit pada saat bersamaan.

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } 

Script (berfungsi di Google Chrome).

Dengan bantuan alat tenun improvisasi kami, kami dapat menggambar berbagai pola:



Namun secara historis, rata-rata orang tidak memiliki lebih dari dua kaki. Oleh karena itu, mudah untuk secara bersamaan menjepit tidak lebih dari dua pedal. Salah satu pola paling populer untuk alat tenun adalah sebagai berikut:



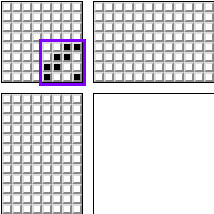
Untuk 4 bingkai. Dan modifikasinya untuk 8 frame:



Tanpa diduga, pola (atau fragmen pola) yang dibuat menggunakan templat ini mirip dengan pola "biliar" kami. Selain itu, pola ini diarsir:



Anda dapat belajar memilih pola "biliar" untuk alat tenun. Contoh:



Di awal artikel, kita sudah melihat sebuah fragmen dari pola ini.

Selesai dengan alat tenun dan tulis skrip untuk memvisualisasikan urutan biner. Kita dapat menyingkirkan salah satu array - polanya simetris diagonal. Bagaimana cara mengisi array yang tersisa? SD:



Kami mengambil urutan untuk $$$\ sqrt {2}$ . Buat sebuah array. Dalam elemen nol array, tulis bit nol dari urutan. Secara bergantian ambil setiap bit urutan. Jika bit ke-1 = 1 - tulis ke array a [n] = a [n-1] +1. Jika bit = 0 - tulis a [n] = a [n-1] -1

$$

$$Q_n = \ lfloor n \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ... \\ a_n = \ begin {cases} a_ {n-1} +1, Q_n = 1; \\ a_ {n-1} -1, Q_n = 0 \ end { kasing}$$

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } 

Kami memeriksa:

  for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 

Faktanya, kita telah menerima fraktal elementer, tetapi kita akan melanjutkan.

Selanjutnya, kita akan berurusan dengan matriks:



Ringkaslah $$$x$ dan $$$y$ . Bagilah modulo dengan 4. Jika hasil yang dihasilkan = 0 atau 1 - tulis dalam matriks true. Untuk 2 dan 3, tulis false. Kita dapat melakukannya tanpa matriks (tidak diketahui sebelumnya apa nilai maksimum dan minimum yang [n] ambil). Ringkas a [x] dan a [y]. Untuk jumlah yang dihasilkan, tambahkan beberapa nomor $$$C$ (untuk menyingkirkan kasus-kasus ketika jumlahnya adalah angka negatif). Bagilah modulo dengan 4. Untuk nilai 0 dan 1, cat di atas piksel dengan koordinat $$$x$ dan $$$y$ .

Algoritma terakhir hanya membutuhkan beberapa baris:

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } 

Visualisasikan urutan fraktal kami.

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Anda dapat dengan mudah memodifikasi skrip untuk mendapatkan gambar RGB:

  q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 

Di atas, kami menambahkan nomor ke jumlah a [x] + a [y] $$$C$ . Jika Anda tidak menambahkan nomor ini, nilai minimum jumlah = -8, maksimum = 8 (untuk $$$x$ dan $$$y$ dari 0 hingga 750). Jika Anda menghapus $$$C$ - dalam beberapa kasus, jumlah berubah menjadi negatif dan bukan kelipatan ke-4 dan untuk kasus-kasus ini piksel tidak dicat (tetap hitam):

  q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 

Anda dapat membayangkannya seolah-olah sebagian dari fraktal berada di bawah beberapa batas imajiner (di bawah batas ini hanya nilai-nilai negatif dikalikan dengan 4 yang dicat: -4, -8, -12, ...).

Kita bisa melihat di mana perbatasan ini:

  if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 

Alih-alih membagi modulo, kita dapat membandingkan jumlah dengan nilai spesifik tertentu dan dengan demikian mengecat hanya satu "lapisan" fraktal. Sebagai contoh, ambil rata-rata antara nilai minimum dan maksimum:

  q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 

Mengubah nilai dari minimum ke maksimum, kita dapat melihat bagaimana "lapisan" dalam dinamika berubah:




Selain itu, kita dapat "di dahi" membandingkan [x] dengan [y] dan juga mendapatkan pola fraktal:

 if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 

Urutan berikut:

$$

$$Q_n = \ lfloor n (\ sqrt {2} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Lapisan tengah:



Dalam dinamika:

$$

$$Q_n = \ lfloor n \ sqrt {3} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Lapisan tengah:



Dalam dinamika:

$$

$$Q_n = \ lfloor n (\ sqrt {3} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Lapisan tengah:



Dalam dinamika:

$$

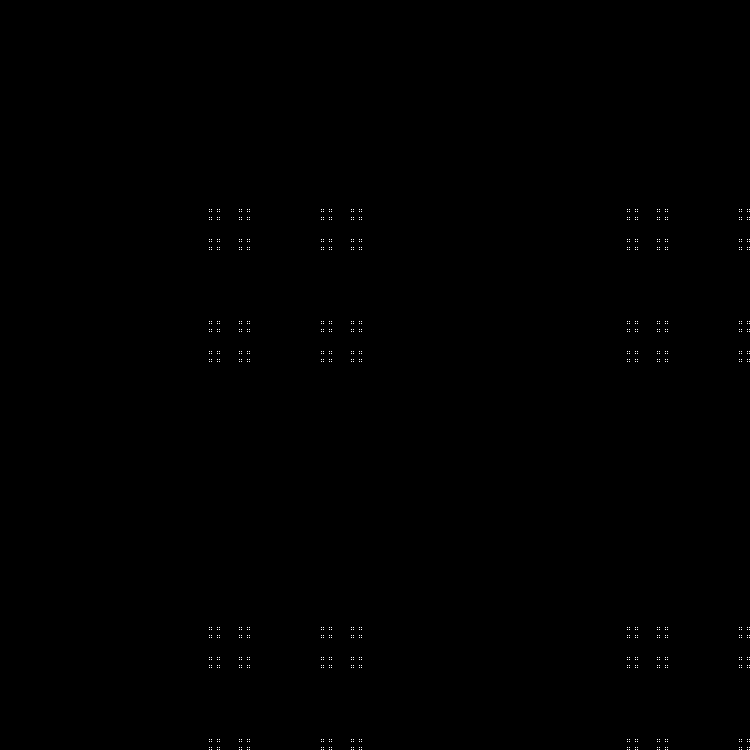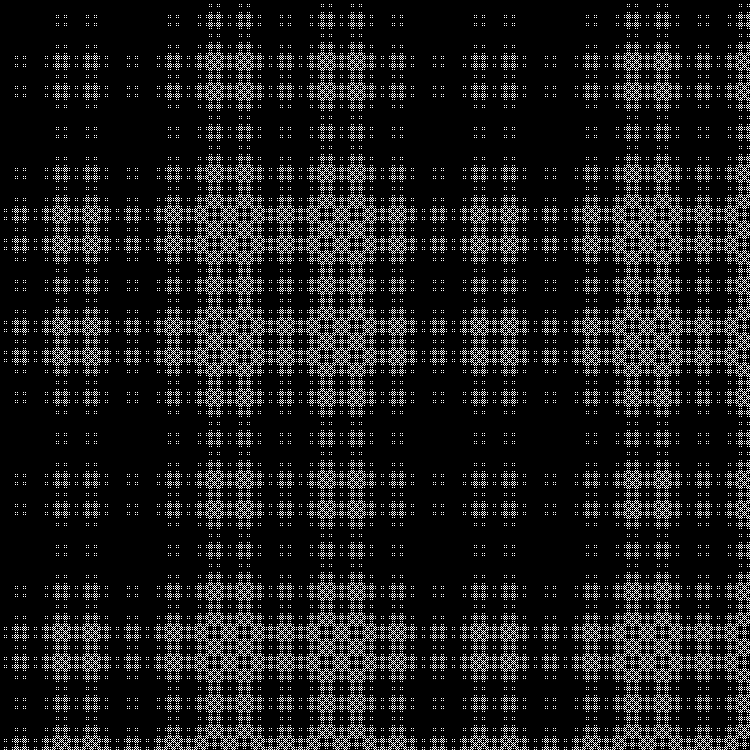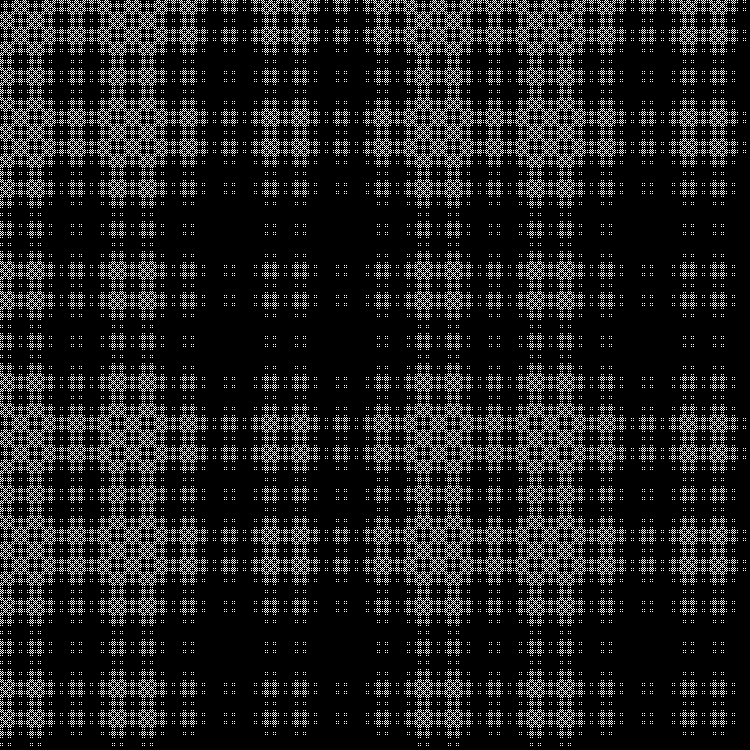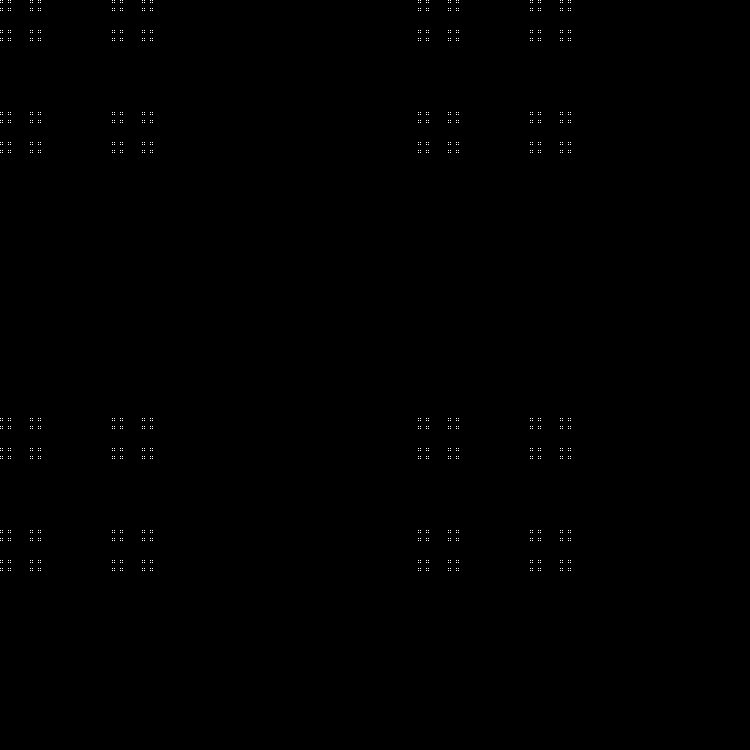
$$Q_n = \ lfloor n \ sqrt {5} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Lapisan tengah:



Dalam dinamika:



Nah, fraktal favorit kami (bagian dari pola ini dapat digambar menggunakan biliar, dengan ukuran sisi sama dengan angka Fibonacci):

$$

$$Q_n = \ lfloor n (\ sqrt {5} +1) \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Fraktal:



RGB:



Lapisan tengah:



Dalam dinamika:



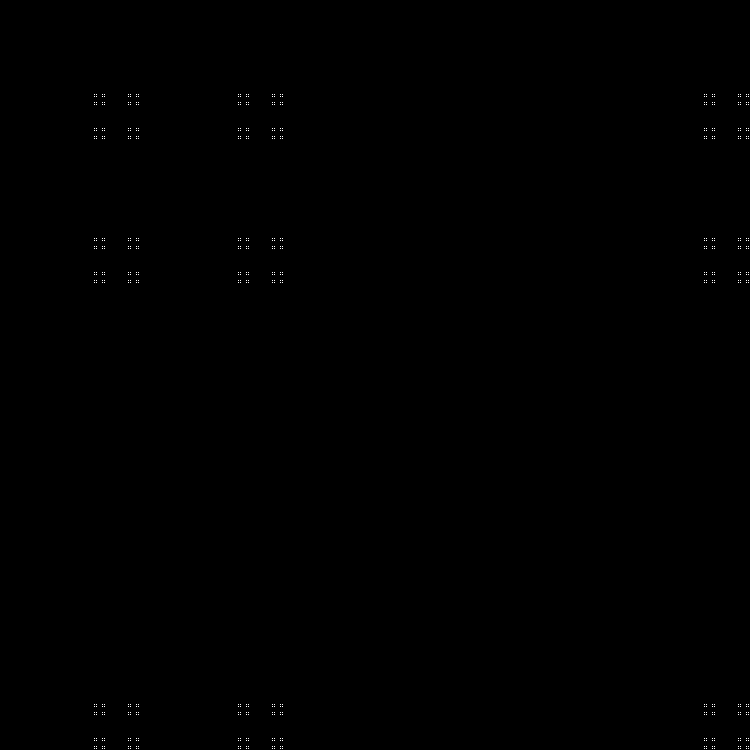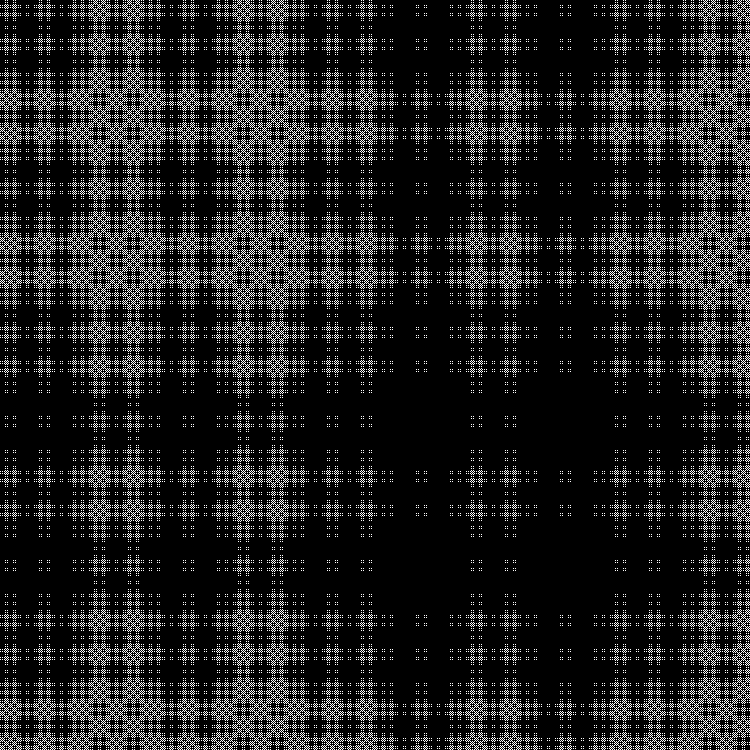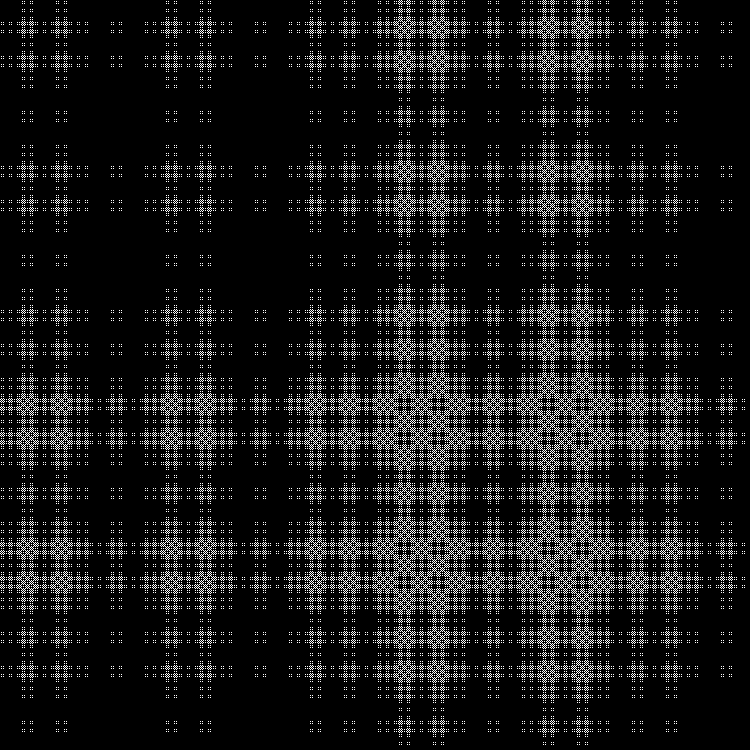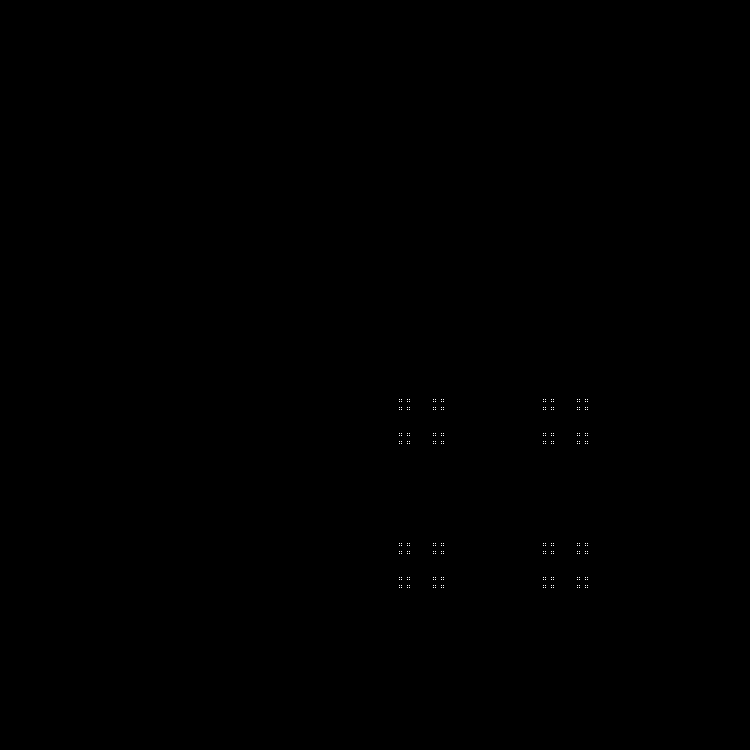
Urutan lain untuk diselesaikan:

$$

$$Q_n = \ lfloor n ^ {2} \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2); \ quad n = 0,1,2, ...$$

Pola:



RGB:



Lapisan tengah:



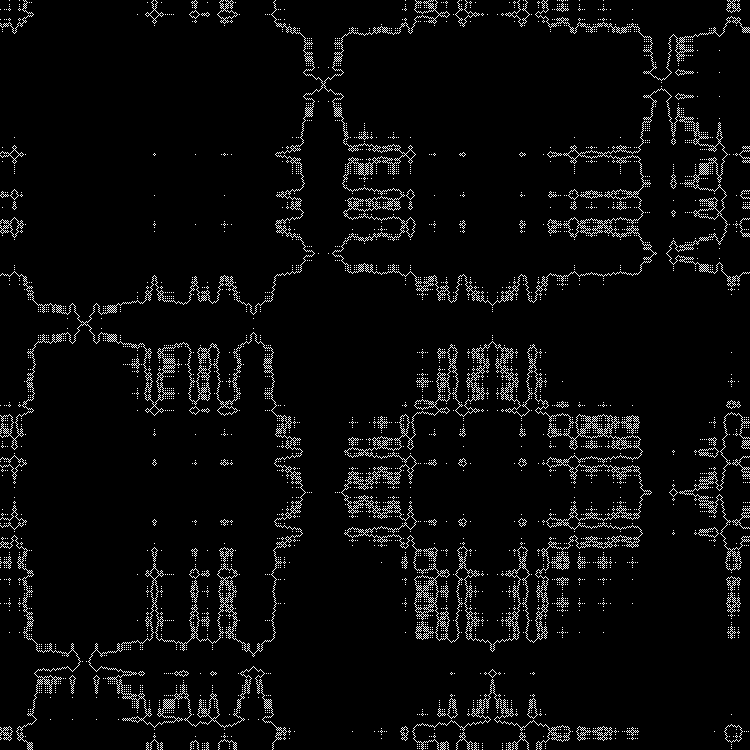
Dalam dinamika:



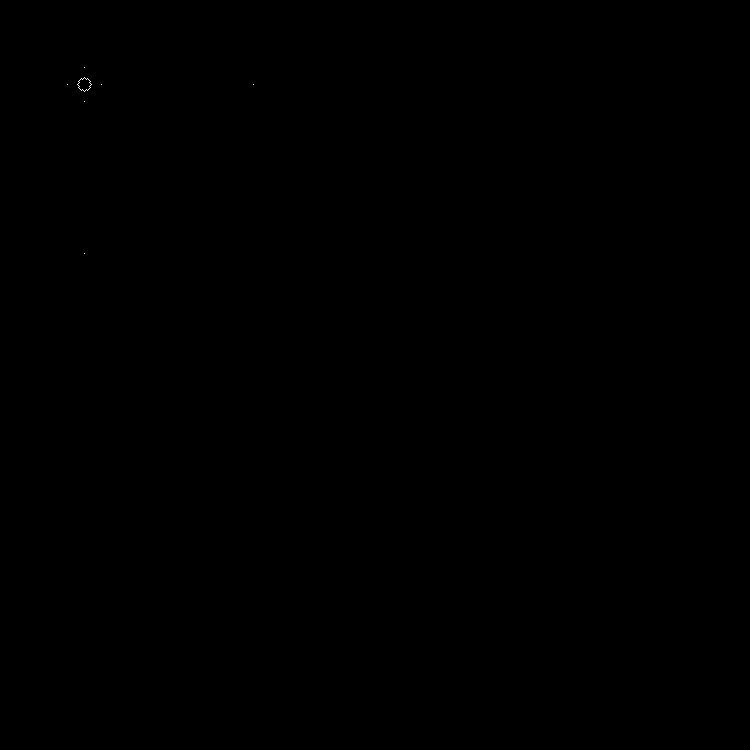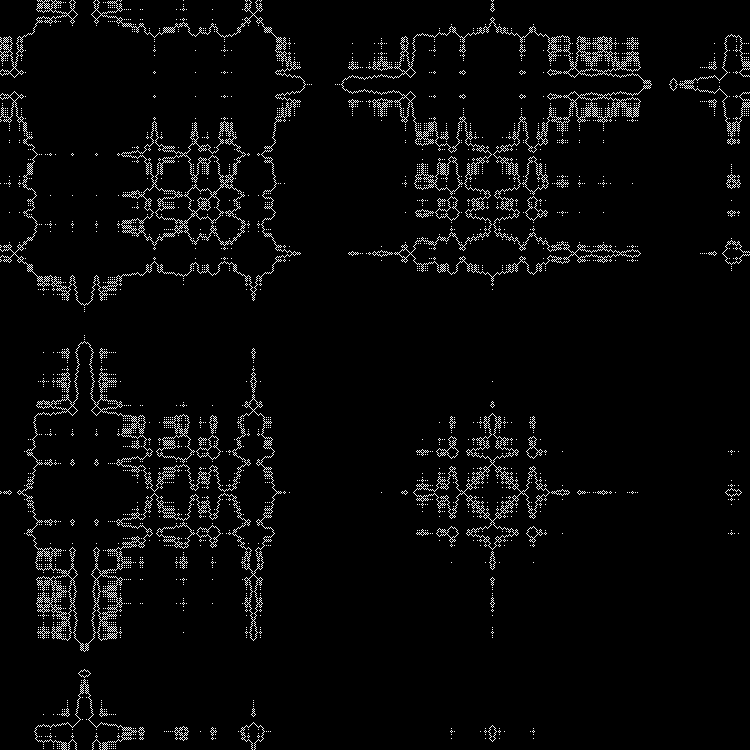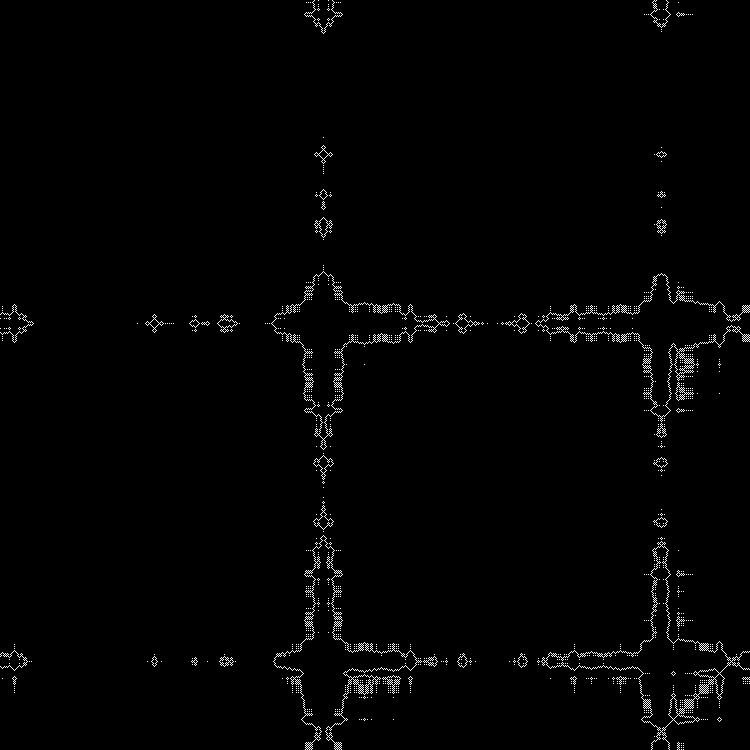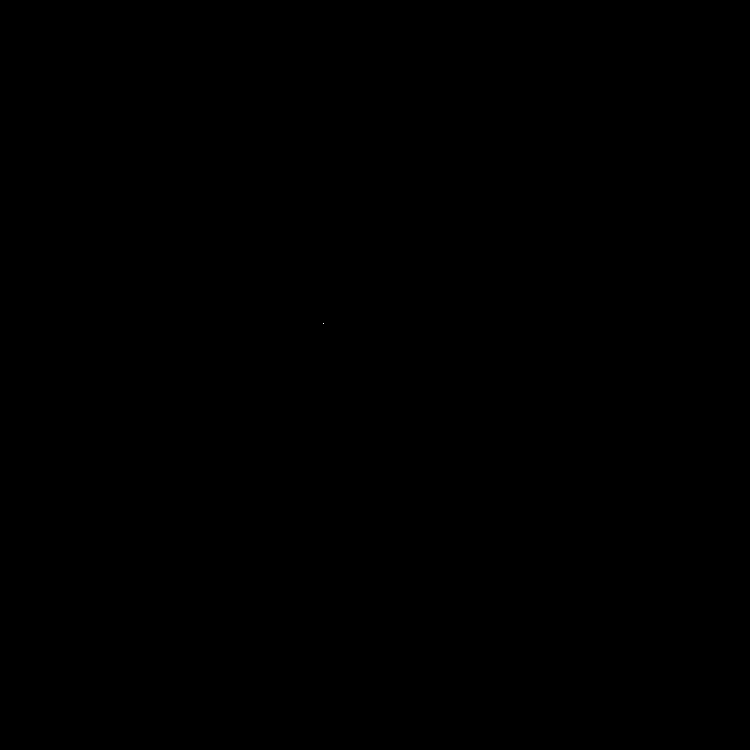
Akar kuadrat lainnya dapat didorong ke dalam skrip . (Anda dapat mengemudi dalam nilai fraksional).

Dalam skrip kedua , Anda dapat mengarahkan urutan secara manual.

Script lain untuk biliar. Koordinat mouse - dimensi biliar. Pola di sebelah kiri terbentuk dari urutan yang diperoleh dengan menggunakan sisa dari divisi (rincian dalam artikel sebelumnya). Di sisi kanan - paritas $$$\ lfloor n \ frac {y} {x} \ rfloor$ .