Perkiraan VaR dan KonVaR untuk harga saham perusahaan Kazakhstani

Dekade terakhir ekonomi dunia secara teratur jatuh ke pusaran krisis keuangan yang telah memengaruhi setiap negara. Ini hampir menyebabkan runtuhnya sistem keuangan yang ada, karena fakta ini, para ahli dalam pemodelan matematika dan ekonomi semua telah menggunakan metode untuk mengendalikan kerugian aset dan portofolio di dunia keuangan (Lechner, LA, dan Ovaert, TC (2010) .Ada kecenderungan yang meningkat terhadap pemodelan matematika dari suatu proses ekonomi untuk memprediksi perilaku pasar dan penilaian keberlanjutannya (ibid). Setelah tanpa perhatian yang diperlukan untuk mengendalikan dan menilai ancaman dengan tepat, semua orang mengerti bahwa hal itu dapat memicu biaya yang luar biasa dalam pengembangan organisasi atau bahkan bangkrut.

Value at Risk (VaR) akhirnya menjadi pendekatan reguler untuk menangkap risiko di antara lembaga-lembaga di sektor keuangan dan regulatornya (Engle, R., dan Manganelli S., 2004). Model ini awalnya diterapkan untuk memperkirakan nilai kerugian dalam portofolio investasi dalam periode waktu tertentu serta pada probabilitas kejadian tertentu. Selain fakta menggunakan VaR di sektor keuangan, ada banyak contoh penilaian nilai berisiko di berbagai bidang seperti mengantisipasi staf medis untuk mengembangkan manajemen sumber daya kesehatan Zinouri, N. (2016). Meskipun sifatnya diterapkan primitif dalam percobaan nyata, model terdiri dari kelemahan dalam evaluasi, (ibid).

Tujuan dari laporan ini adalah deskripsi model VaR yang ada termasuk salah satu versi pemutakhirannya, yaitu, Nilai Bersyarat pada Risiko (CVaR). Di bagian berikutnya dan bagian 3, algoritma evaluasi dan pengujian model dijelaskan. Untuk ilustrasi yang jelas, kerugian yang diperkirakan diperkirakan pada aset salah satu perusahaan Kazakhstan yang diperdagangkan di pasar bursa keuangan dalam periode waktu yang lama. Bagian terakhir 4 dan 5 membahas dan mendemonstrasikan temuan pekerjaan penelitian.

Latar belakang

Diyakini bahwa penggunaan VaR pertama oleh organisasi keuangan raksasa hingga 40 tahun yang lalu dan sebagai akibatnya VaR telah menjadi populer di antara perusahaan perdagangan lainnya, bahkan regulator keuangan telah memperhatikan model tersebut (Linsmeier, TJ, dan Pearson, ND 2000). Sebagai contoh, Komisi Sekuritas dan Bursa AS menuliskan VaR pada daftar metode kuantitatif untuk menghitung risiko pasar dan properti pada tahun 1997 (ibid).

Sebenarnya, menurut artikel Lechner, LA, dan Ovaert, TC (2010) serta Linsmeier, TJ, dan Pearson, ND (2000), VaR adalah persamaan estimasi yang diekspresikan dalam satuan moneter yang tidak melebihi kerugian dalam kisaran besarnya. selama periode waktu tertentu dan diberikan tingkat kepercayaan. Biasanya, tingkat kepercayaan estimasi model (99%, 97,5%, 95%) atau dengan kata lain probabilitas bahwa beberapa kasus yang tidak menguntungkan akan terjadi dan pengaruh pada pasar sama dengan 1, 2,5 dan 5 persen (ibid).

Persamaan VaR yang terkenal dapat dijelaskan (Phelps S, 2018):

$$$(1) \ VaR (X) = \ min \ \ {x \ \ epsilon \ R: 1-F_x (-x) \ geq \ alpha \}$

Di mana X adalah variabel acak yang melakukan jumlah nilai portofolio, dan merupakan fungsi distribusi kumulatif (ibid).

Di sisi lain, Hooper GP (1996, dikutip dalam Lechner, LA, dan Ovaert, TC 2010) menunjukkan VaR dengan kepercayaan alpha yang didefinisikan dengan cara yang sangat mendasar:

$$$(2) \ VaR ^ \ alpha (X) = \ sigma \ sqrt {\ delta t} N ^ {- 1} \ alpha$

Dimana $$$\ sigma$adalah standar deviasi dari pengembalian saham yang dipilih, $$$\ delta t$adalah akar kuadrat dari periode waktu tetap dan $$$N ^ {- 1}$adalah fungsi distribusi kumulatif (CDF) untuk distribusi normal (Lechner, LA, dan Ovaert, TC 2010).

Meskipun VaR adalah metode yang terkenal dan ditangani untuk memperkirakan risiko portofolio yang telah diputuskan, ada beberapa kekurangan dalam kasus ketika mengukur kerentanan terhadap masalah-masalah pasar utama, yaitu, contoh terkait dengan kemungkinan peristiwa pasar ekstrem tidak cukup terperangkap di ekor. dari distribusi normal (Capiński, MJ 2015). Untuk mengatasi masalah ini, Nilai Bersyarat pada Risiko (CVaR) dibuat yang mempertimbangkan nilai kerugian yang diharapkan, bukan VaR (ibid). CVaR didefinisikan sebagai:

$$$(3) \ CVaR ^ \ alpha (X) = \ frac {1} {\ alpha} \ int ^ \ alpha_0 VaR ^ \ beta (X) d \ beta = \ frac {-1} {\ alpha} q ^ \ beta (X) d \ beta$

$$$(4) \ CVaR ^ \ alpha (X) = - \ frac {1} {\ alpha} (E [X 1 _ {\ {X \ leq q ^ \ alpha (x) \}}] + q ^ \ alpha (X) (\ alpha-P [X \ leq q ^ \ alpha (X)]))$

Dimana Ahn D.-H. et.al (1999, dikutip dalam Capiński, MJ 2015) menafsirkan $$$-q ^ \ alpha (X)$
sebagai VaR dari variabel acak X (pengembalian harga saham) dengan probabilitas $$$\ alpha$dan mendefinisikan sebagai kuantil atas X.

Selain itu, Acerbi C. dan Tasche D. (2002, dikutip dalam Capiński, MJ 2015) mengkonfirmasi, "CVaR adalah ukuran risiko yang koheren". Rockafellar, RT, dan Uryasev, S. (2000) memperhatikan bahwa CVaR memiliki fitur tambahan: transisi-equivarian, positif homogen, cembung, dll.

Bab berikut dari artikel ini menunjukkan implementasi Value at Risk (VaR) dan Value Conditional Value at Risk (CVaR) juga diumumkan sebagai kekurangan yang diharapkan dalam pekerjaan Rockafellar, RT, dan Uryasev, S. (2000) dengan menggunakan teknologi informasi pada data nyata.

Metodologi

Biarkan mempertimbangkan metode yang paling umum digunakan untuk menghitung VaR, serta kelebihan dan kekurangannya.

Menurut laporan Lechner, LA, dan Ovaert, TC (2010), simulasi historis adalah pendekatan luas untuk mengevaluasi VaR dan modifikasinya. Dalam pemodelan historis data, kami mengambil nilai-nilai fluktuasi keuangan untuk portofolio yang sudah diketahui dari pengukuran sebelumnya. Oleh karena itu hanya urutan logis bahwa kelemahan dari metode ini adalah ketidakmungkinan membangun prediksi untuk portofolio tanpa sepotong informasi tentang itu. Metode Monte Carlo dalam banyak hal identik dengan metode pemodelan historis, yang digunakan untuk teknik akurasi tinggi, perbedaan utama yang jelas bahwa perhitungan simulasi Monte Carlo tidak didasarkan pada data nyata, tetapi diwujudkan pada nilai-nilai yang dihasilkan secara acak. Keuntungan dari metode ini adalah kemungkinan untuk mempertimbangkan sebagai sejumlah besar situasi, dan meniru perilaku pasar dalam kondisi ekstrim serta tidak perlu ada perkiraan antara faktor risiko dan perubahan dalam portofolio (Glasserman, P., Heidelberger, P . dan Shahabuddin, P., 2002). Kelemahan yang jelas adalah sumber daya komputasi besar yang diperlukan untuk mengimplementasikan pendekatan ini (ibid).

Tentu, ini bukan satu-satunya metode untuk menghitung model VaR. Selain itu, ada kedua model prediksi harga linear dan kuadrat sederhana, dan metode variasi yang agak rumit, yang tidak tercakup dalam esai.

Analisis data

Sebagai data sekunder untuk menguji penilaian yang akurat, stok KAZ Minerals diambil. Untuk memperjelas pekerjaan, harga tertutup Disesuaikan diambil untuk simulasi dalam model. Saham perusahaan Mineral KAZ (KAZ.L) adalah salah satu dari sekuritas perdagangan yang berhasil di antara perusahaan-perusahaan Kazakhstani di London Stock Exchange (LSE) serta dikategorikan dalam daftar Premium Equity Commercial Companies (London Stock Exchange, 2019). Entitas hadir sebagai perusahaan tambang tembaga besar-besaran di Kazakhstan (Kazminerals.com. 2019).

Data historis harga saham diunduh dari situs web Yahoo Finance (Finance.yahoo.com, 2019). Untuk memastikan validitas pekerjaan, periode satu tahun dari 22 Maret 2018 hingga 22 Maret 2019 diamati. Selanjutnya, untuk menghindari gangguan informasi, dalam analisis, data historis harga saham KAZ.L diunduh dalam format Comma-Separated Values ​​(CSV) karena fakta bahwa format CSV kompatibel dengan program Microsoft Excel (Excel) . Data yang dipilih dari proyek disajikan sebagai grafik garis dengan menggunakan Excel pada Gambar 1.

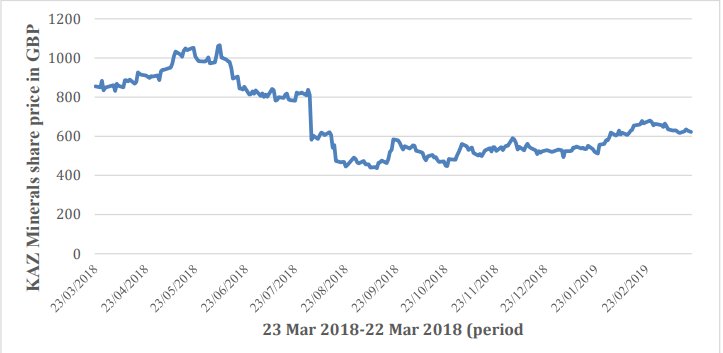
Gambar 1. Dinamika perubahan harga saham KAZ Mineral selama satu tahun

Karena keterbatasan garis waktu laporan, alih-alih menggunakan bahasa pemrograman seperti Python untuk implementasi model penilaian, data dianalisis sepenuhnya dalam Excel.

Temuan

Pada bagian sebelumnya, model untuk memperkirakan potensi kerugian dalam portofolio berdasarkan persamaan VaR dan CVaR dan menggunakan perubahan harga saham KAZ Minerals dari 23 Maret 2018 hingga 23 Maret 2019, diunduh dari sumber web resmi Yahoo Finance (Finance.yahoo. com, 2019). Kedua persamaan dieksekusi untuk setiap tanggal dari periode yang dipilih.

Tabel 1 menunjukkan pengembalian harian bisnis rata-rata, standar deviasi pengembalian, nilai minimum pengembalian dan nilai maksimum pengembalian untuk contoh ini.

Tabel 1. Bagikan pengembalian rata-rata dan standar deviasi pengembalian

Rata-rata yang sesuai adalah -0.0006 dan standar deviasi 0,0355 dari pengembalian untuk mineral KAZ keamanan unik yang dipilih. Terlebih lagi bahwa varian pengembalian adalah 0,0013. Selain itu, yang tentunya harus digarisbawahi bahwa dalam karya penelitian Vee, DNC, dan Gonpot, P. N (2014) pengembalian saham Kazakhstani menunjukkan nilai signifikan dalam volatilitas namun estimasi terkait dengan indeks Bursa Efek Kazakhstan pada pra dan pasca periode 2008. Juga, harus disebutkan bahwa nilai maksimum di antara pengembalian adalah 0,0998, serta nilai minimum di antara pengembalian adalah -0,2829 dalam distribusi kerugian. Tabel 2 menyajikan nilai maksimum dan minimum di antara harga saham dekat yang disesuaikan (KAZ.L) dalam perdagangan Pound Sterling (GBP) di London Stock Exchange dari 23 Maret 2018 hingga 22 Maret 2019.

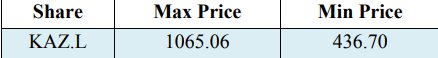
Tabel 2. Harga saham KAZ Mineral maksimum dan minimum dalam GBP

Langkah berikut adalah evaluasi Value at Risk (VaR) dan Conditional Value at Risk (CVaR) untuk tingkat kepercayaan - 0,99, 0,972 dan 0,95. Nilai-nilai diungkapkan pada Tabel 3.

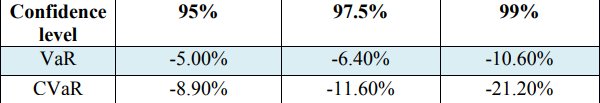
Tabel 3. Nilai VaR dan CVaR dari pengembalian

Ukuran sampel simulasi diambil 252 unit dari 23 Maret 2018 hingga 22 Maret 2019 selama satu tahun.

Diskusi

Dalam laporan tersebut, persamaan VaR dan CVaR menunjukkan nilai yang dapat dipercaya jika model estimasi untuk harga saham perusahaan Kazakhstani dalam periode jangka pendek. Dengan nilai-nilai ini di satu sisi, kedua metode menyajikan hasil yang memadai untuk menilai nilai ancaman untuk portofolio investasi (Linsmeier, TJ, dan Pearson, ND 2000; Lechner, LA, dan Ovaert, TC 2010).

Selain itu, menurut temuan dari Tabel 2, pemberitahuan berikutnya langsung bahwa nilai-nilai untuk CVaR lebih besar dibandingkan dengan nilai VaR oleh semua ukuran tingkat kepercayaan. Dapat diberikan penjelasan oleh fakta bahwa CVaR mengambil risiko rata-rata portofolio yang dipilih karena itu lebih sensitif pada ekor distribusi kerugian daripada VaR. Ini membuktikan sekali lagi bahwa CVaR adalah risiko yang koheren (Acerbi C. dan Tasche D., 2002, dikutip dalam Capiński, MJ 2015; Rockafellar, RT, dan Uryasev, S. 2000). Sebagai contoh, berkenaan dengan kecukupan dari kedua model estimasi, dengan tingkat kepercayaan 99% VaR dan CVaR menggambarkan persentase kerugian signifikan dari pengembalian saham. Lebih tepatnya, mungkin terdeteksi VaR -10,60% dan CVaR -21,20%. Cukup jelas alasan tindakan kolosal CVaR dengan tingkat kepercayaan yang diberikan 99% karena fakta kisaran harga saham selama periode tersebut, harga maksimum adalah 1065,06 GBP harga saham minimum masing-masing adalah 436,70 GBP.

Kesimpulan

Setelah mempertimbangkan semua hal di atas, harus jelas disebutkan lagi bahwa tujuan dari laporan ini adalah untuk menunjukkan estimasi nilai kemungkinan kerugian untuk perusahaan Kazakhstani (KAZ Minerals) selama periode dari 23 Maret 2018 hingga 22 Maret 2019. dibentuk pada persamaan Value at Risk (VaR) dan Conditional Value at Risk (CVaR). Penampilan dari simulasi dibandingkan satu sama lain dalam periode waktu yang sama. Hasilnya menunjukkan nilai signifikan untuk setiap metode dan membuktikan pekerjaan sebelumnya pada area yang sama bahwa CVaR memiliki ukuran yang lebih akurat dibandingkan dengan VaR (Acerbi C. dan Tasche D., 2002, dikutip di Capiński, MJ 2015; Rockafellar, RT, dan Uryasev, S.2000).

Terlepas dari kritik, VaR merupakan alat yang tersebar luas di semua lembaga keuangan hingga saat ini dan ada banyak versi modifikasinya. Karena hambatan perhitungan yang rumit dalam penelitian mendalam, percobaan dilakukan dengan menggunakan Microsoft Excel alih-alih menggunakan bahasa pemrograman seperti Python, serta hasilnya diungkapkan dalam laporan. Hasil esai dapat menjadi ruang bawah tanah untuk pekerjaan lebih lanjut dalam menggunakan ukuran penilaian risiko yang kompleks untuk portofolio di industri bursa, industri asuransi dan industri investasi.