Di bawah ini kita akan mengatakan beberapa kata tentang alternatif waktu diskrit untuk model matematika dalam bentuk persamaan diferensial linier, yang secara umum diketahui tetapi agak tidak terduga untuk insinyur, yaitu, model autoregresif - rata-rata bergerak, dan prospek yang sangat tidak biasa untuk pemodelan seperti itu, kemampuan yang secara signifikan melebihi apa yang biasa Anda dapatkan dari LDU.
Daftar kapabilitas potensial teknologi mencakup analisis sistem dengan gangguan masuk yang tidak dapat diakses untuk observasi, penentuan sifat resonansi sistem tersebut, spektrum dan proses eksitasi eksternal, estimasi spektral proses dengan realisasi singkatnya, pemodelan perilaku sistem pada frekuensi sampling rendah dari waktu ke waktu, dll.

Proses ARMA, yang dikenal oleh para ekonom (lebih tepatnya, "ahli ekonometrika"), kurang dikenal oleh para spesialis dalam regulasi otomatis, dan, menurut pendapat saya, hampir tidak digunakan oleh insinyur mesin dan insinyur radio-elektronik, terutama yang "sekolah tua". Artikel ini mencoba untuk menunjukkan beberapa area penerapan teori ARMA dalam praktik teknik.
Singkatnya, disederhanakan, bagi mereka yang tidak terbiasa dengan subjek, tentang yang sebenarnya. Proses waktu kontinu stokastik x (t) untuk alasan "digital" yang jelas dalam praktek biasanya cocok dengan urutan waktu diskrit x [i] dengan interval pengambilan sampel Δt.
Pada prinsipnya, untuk setiap proses x [i] representasi bentuk dimungkinkan
x [i] - a 1 · x [i-1] - a 2 · x [i-2] - ... - p · x [ip] = b 0 · f [i] + b 1 · f [i- 1] + ... + b q · f [iq] (1),
di mana
k dan b
k adalah koefisien konstan (untuk model ini), yang disebut model rata-rata autoregresi dengan urutan autoregresi p dan rata-rata bergerak q. atau ARMA (p, q) -model, f [i] adalah semacam proses "masuk", yang sedikit lebih rendah. Seringkali (1) ditulis dalam bentuk yang sedikit berbeda (6).
Pada dasarnya, ini hanya filter digital yang memiliki bagian MA rekursif dan non-rekursif.
Ada korespondensi antara model ARMA (p, q) dan sistem linier (misalnya, mekanik), misalnya, dijelaskan oleh persamaan diferensial linear yang terkenal dari bentuk
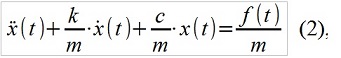
di mana m, c, k adalah massa, kekakuan dan redaman dari sistem mekanis, f (t) adalah gaya eksternal. Mitra ARMA terlihat seperti ini:
x [i] - a 1 · x [i-1] - a 2 · x [i-2] = b 1 · f [i-1] (3),
koefisien model dapat dengan mudah ditemukan melalui nilai eigen λ
1 dan λ
1 * (untuk singkatnya, kasus "berosilasi" dipertimbangkan) dari sistem linear dan :t:
a
1 = z + z *, a
2 = - z · z *, b
1 = j (z * -z) · Δt / (2mω
1 ),
di mana z = exp (λ
1 · Δt), λ
1 = -ε
1 + jω
1 , j adalah unit imajiner, * adalah konjugasi kompleks
untuk referensi:

Untuk sistem pengujian, m = 1 kg, c = 100 N / m, k = 0,75 kg / s, Δt = 0,12 s.,
diperoleh ARMA (2,1) -model
x [i] - 0,69433x [i-1] +0.91393 x [i-2] = 0,010696f [i-1](Penjelasan yang sangat singkat tentang bagaimana (3) diperoleh dari (2). Fungsi transisi pulsa dari sistem linier kami, yaitu, respons sistem ke satu pulsa:
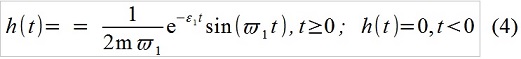
Rekam (2) dalam bentuk "integral" disebut "konvolusi" f (t) dan h (t), artinya melibatkan tindakan eksternal sebagai urutan impuls elementer. Dalam waktu yang terpisah, tulis, misalnya, seperti ini:
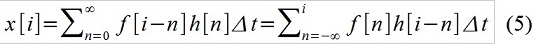
Dengan menambahkan x [i], x [i-1] dan x [i-2] menggunakan faktor-faktor yang dipilih 1, a dan
2, mereka mencapai penghancuran timbal balik dari “ekor” tak terbatas h [i] - di sisi kanan adalah f [i] · H [0] = f [i] · 0 dan f [i-1] · h [1] = f [i-1] · b
1 . Dari sudut pandang teori ARMA, model dimensi tak terbatas MA rata-rata bergerak (∞) ditransformasikan menjadi ARMA (2,1) (walaupun beberapa akan mengatakan bahwa model autoregresif murni AR (2) = ARMA (2,0) diperoleh secara kebetulan.
Catatan 1. Seorang pembaca yang terbiasa dengan pemrosesan digital dari proses akan mengatakan bahwa hanya mendiskritisasi h (t) tidak terlalu benar - perlu untuk membatasi fungsi h (t) dalam frekuensi hingga 1 / (2Δt) (untuk menyaring). Kalau tidak, ada kesalahan masking frekuensi. Grafik respons frekuensi dan respons fase sistem kami, model "analitik" dan ARMA, menunjukkan mengapa kesalahan ini dalam sebagian besar kasus rekayasa kemungkinan besar dapat diabaikan (Gbr. 1) (di sini, respons frekuensi berada pada skala logaritmik).
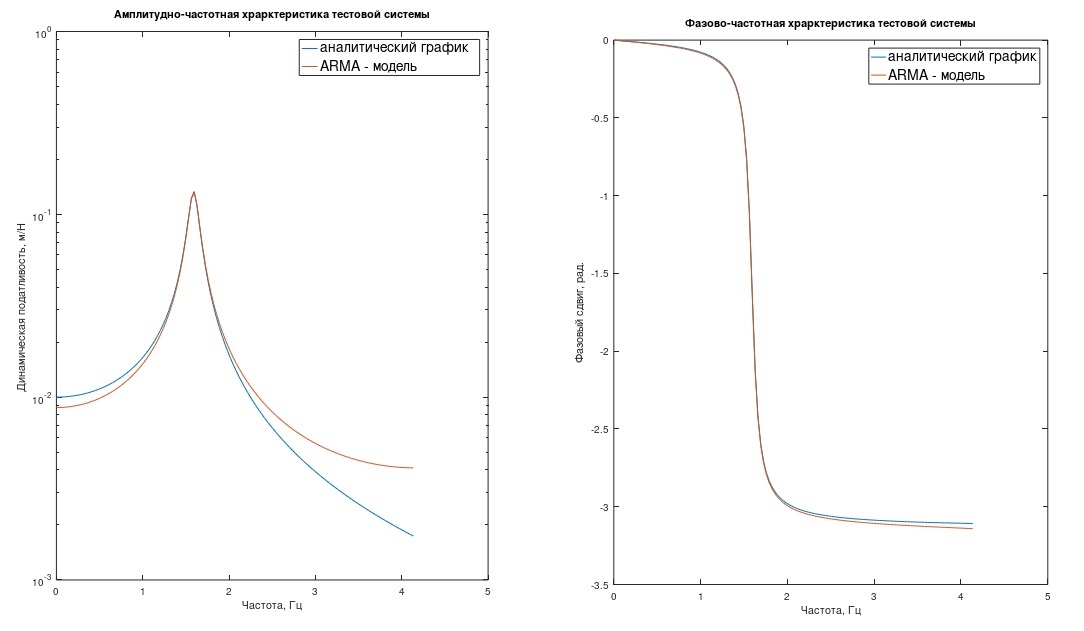
Gbr. 1 Respons frekuensi dan respons fase dari sistem uji.
Catatan 2. Dalam praktiknya, urutan model ARMA dapat secara signifikan lebih besar daripada contoh yang dipertimbangkan di atas, karena, katakanlah, beberapa derajat kebebasan sistem mekanis atau spektrum kompleks pengaruh eksternal nyata.
Komentar 3. Sangat penting. Ada metode (tidak dipertimbangkan di sini - lebih banyak artikel dapat ditulis tentang mereka) yang memungkinkan seseorang untuk memperkirakan parameter model ARMA (yaitu, urutan model p dan q dan koefisien a
k dan b
k ) hanya dengan proses yang dihasilkan x [i], dengan asumsi bahwa f [i] adalah white noise hipotetis yang variansinya juga dapat diperkirakan. Secara umum, penilaian semacam itu adalah bagian utama dari keseluruhan teori ARMA. Meskipun metode-metode ini tidak berbeda dalam kesempurnaan tertentu, mereka sangat menarik.
Sekarang tentang mengapa, pada kenyataannya, semua ini dapat (atau bisa) diterapkan dalam praktik. Selain yang cukup jelas - konstruksi cepat sinusoid "manual" teredam (dan tidak basah) dari dua titik pertama dan dua koefisien a
1 dan
2 , ada, menurut pendapat saya, aplikasi yang lebih serius dari model-model ini dalam praktek teknik.
1. Nah, sebenarnya, untuk simulasi operasi sistem - kami memberikan sinyal eksternal nyata f [i] ke input, kami mendapatkan x [i] pada output:
x [i] = a 1 · x [i-1] + a 2 · x [i-2] + ... + a p · x [ip] + b 0 · f [i] + b 1 · f [i- 1] + ... + b q · f [iq] (6)
Model ARMA mengatasi tugas dengan lebih baik daripada model beda hingga, namun, ini hanya terlihat pada interval pengambilan sampel besar Δt. (pada Gambar. 2, Δt = 0,12 dtk (kiri) dan 0,03 dtk). Dalam kasus apa masuk akal untuk mengacaukan ARMA - Anda yang memutuskan.
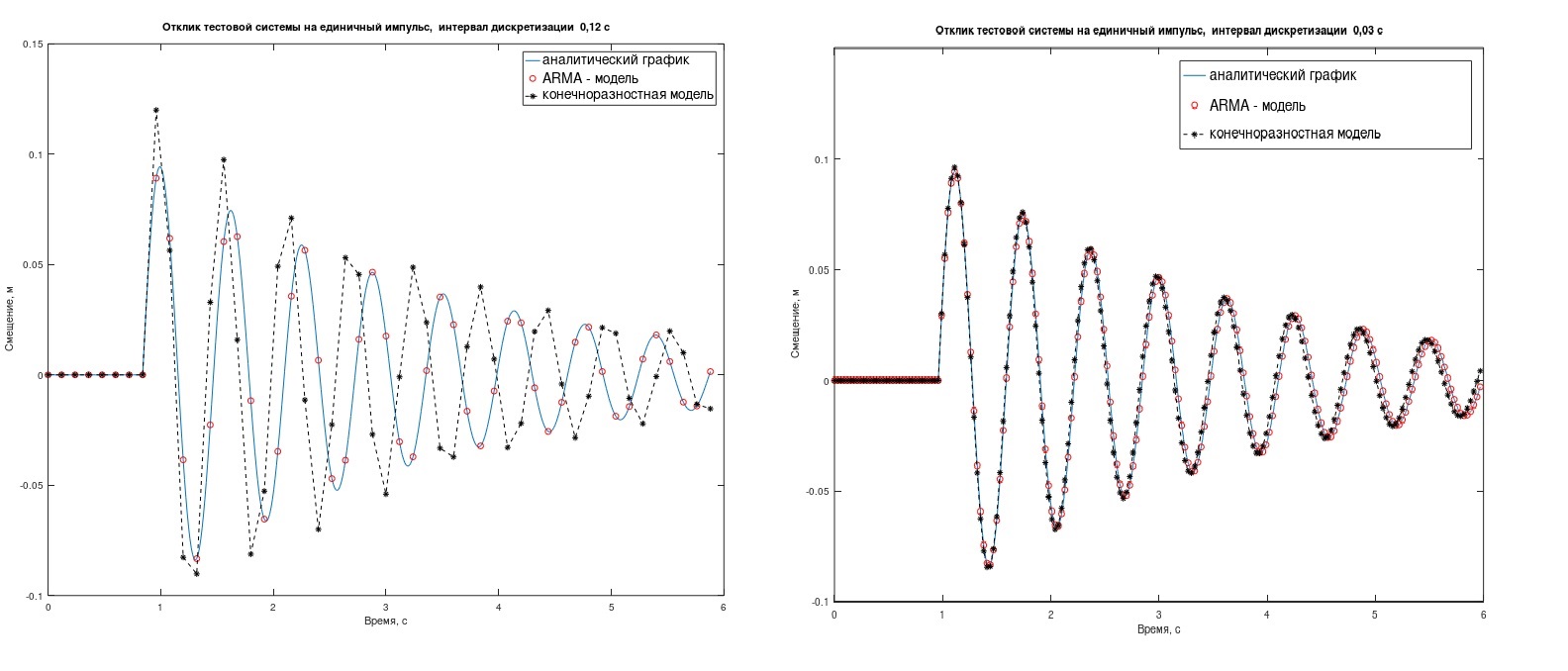
gbr. 2. Respon sistem uji terhadap satu impuls.
2. Untuk estimasi spektral, terutama ketika panjang implementasi proses stasioner tidak cukup untuk observasi. Mungkin ini adalah aplikasi teknik paling terkenal dari model ARMA. Karena filter digital tertentu dan varian white noise yang masuk itu akan diperoleh untuk proses yang sedang dipelajari, tugas membangun perkiraan PSD diselesaikan dengan cara yang jelas. Memang, dimungkinkan untuk mendapatkan grafik SPM eksternal yang sangat "halus" dan pada saat yang sama menciptakan kesan resolusi tinggi. Peningkatan yang diharapkan dalam penilaian dikaitkan dengan fakta bahwa peneliti membawa informasi eksternal tentang sifat proses ke konstruksi penilaian - biasanya dengan menetapkan urutan model yang dikenal.
Singkatnya, Anda perlu tahu bagaimana kira-kira PSD ini akan terlihat. Studi "eksplorasi" dari implementasi ini menggunakan metode klasik tidak banyak membantu, kebanyakan merujuk pada studi klasik (berdasarkan FFT) yang sifatnya serupa, tetapi realisasi yang jauh lebih lama. Ada kemungkinan kesalahan besar.
3. Untuk analisis sifat resonansi sistem dan spektrum aksi eksternal, dalam kasus ketika efek eksternal sebenarnya tidak tersedia untuk pengamatan. Seperti yang telah dicatat, adalah mungkin, mengetahui proses x [i], untuk menentukan semua koefisien model a
k dan b
k (dan varian dari white noise yang masuk). Dengan menggunakannya, menentukan akar dua polinomial dengan koefisien yang sesuai, mudah untuk menemukan p "kutub" dan q "nol" dari model (λ
k dan μ
k ) dan membangun fungsi transfernya - Anda mungkin bahkan tidak dapat menggunakan formulir ARMA (di sini diberikan), dan dalam bentuk "analitis" seperti biasa - seperti yang kami temukan di atas (Gbr. 1), perbedaannya kecil. Misalnya, untuk p = 5, q = 3 (sementara abstrak dari yang ada, tampaknya, pembatasan rasio p dan q), sebagai opsi, kami memiliki:
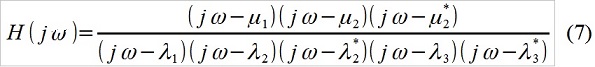
Semuanya sangat, sangat sederhana, tentu saja. Berdasarkan sifat objek yang diteliti diketahui (misalnya, ini adalah tes poligon dari kelancaran perjalanan mobil) dan dampak eksternal (mikroprofil jalan), peneliti memutuskan untuk menulis ulang fungsi transfer, misalnya, seperti ini:
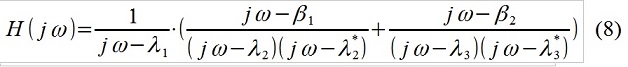
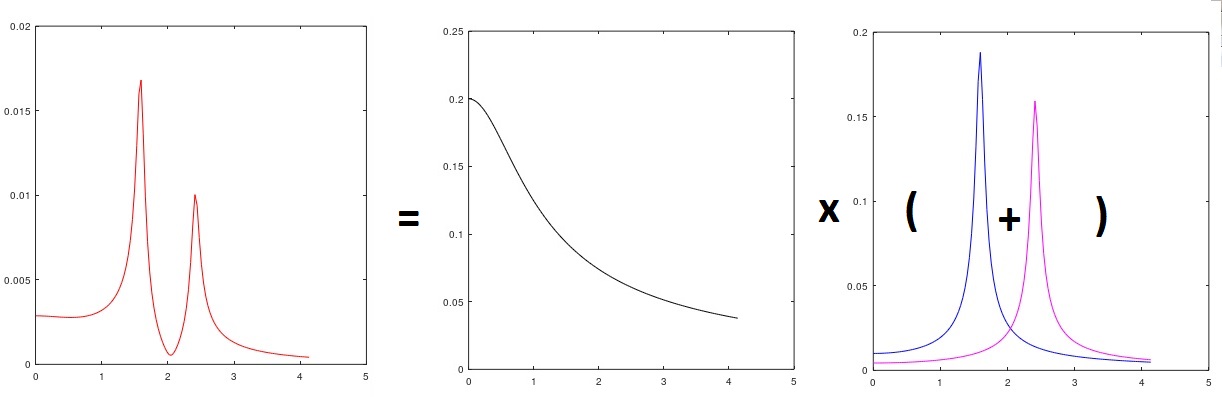
Gambar. 3 Analisis spektrum sinyal dengan alokasi gangguan yang masuk
dan berkomentar - bagian dari model yang terkait dengan λ
1 jelas (hingga mengkuadratkan dan mengalikannya dengan varian dari white noise hipotetis yang masuk) mikroprofil "merah muda" jalan (Gbr. 3) (yaitu, kami mengidentifikasi spektrum yang tidak diketahui dari nyata sinyal input - dipilih secara manual - tampaknya "mirip"), λ
2 dan λ
3 adalah properti resonansi tubuh pada suspensi (mungkin mode longitudinal-angular dan vertikal getaran). Masalah utama akan, tentu saja, dalam menentukan parameter model ARMA. Untuk yang baru saja dijelaskan, Anda kadang-kadang dapat, tanpa ARMA, "merangkak" dengan cara kuno (meskipun dalam bentuk elektronik) sesuai dengan grafik kerapatan spektral dan mengukur lebar puncak pada level -3 dB, dll., Atau menerapkan curvitting, kadang-kadang bahkan dengan kesuksesan besar .
3. Untuk prediksi linier x [i]. Rupanya, aplikasi utama ARMA adalah untuk para ahli ekonometrika. Terlihat dari (6) bahwa, jika koefisien model diestimasi dengan menggunakan metode yang diuraikan di atas, nilai x berikutnya [i] dapat diestimasi akurat menjadi white noise hipotetis yang tidak dapat diakses oleh pengamatan b
0 · f [i], varian white noise ini diperkirakan bersama dengan koefisien model. Biasanya dalam kasus ini, penyesuaian dinamis dari parameter model tersirat. Tampaknya, ini dapat berguna dalam sistem getaran aktif dan pengurangan kebisingan. Spesialis TAP paling tahu.
4. Untuk mengembalikan proses yang tidak dapat diakses yang tidak dapat diamati. Ketika membagi model menjadi beberapa bagian, seperti yang ditunjukkan di Bagian 3, berdasarkan pengetahuan tentang sifat proses yang diteliti, dimungkinkan untuk mengevaluasi secara terpisah spektrum gangguan yang masuk, dan secara terpisah, sifat osilasi sistem fisik (pisahkan model menjadi beberapa bagian). Anda dapat melangkah lebih jauh - membuat filter (model ARMA, kebalikan dari model asli) yang menghubungkan output sistem dengan input, dan dengan bantuannya dari proses yang dihasilkan x [i] mendapatkan implementasi sementara dari gangguan yang masuk. Misalnya, coba pulihkan sinyal yang tidak terdistorsi yang direkam dengan distorsi linier yang tidak diketahui oleh peralatan yang tidak tersedia untuk studi terpisah (misalnya, diperoleh dengan telemetri).
Berdasarkan pengetahuan saya yang sederhana, sebagai hasilnya saya akan mengungkapkan penilaian subyektif tersebut. Penerapan teknologi ARMA untuk masalah teknik sangat tergantung pada kesempurnaan metode untuk memperkirakan parameter model ini dari sinyal yang dihasilkan, atau lebih tepatnya, menurut pendapat saya, sangat terkendali oleh ketidaksempurnaan metode ini. Akumulasi pengalaman dalam penerapan ARMA di bidang teknik tampaknya masuk akal, terutama, untuk mengantisipasi "terobosan" yang sangat mungkin di bidang ini.