Kata Pengantar

Saya pikir kita perlu menjelaskan secara singkat mengapa tiba-tiba topik yang tampaknya sepele dengan perhitungan anggaran energi dan mengapa tepatnya satelit CubeSat? Nah, semuanya cukup sederhana di sini: praktik mengajar singkat saya menunjukkan (kepada saya) bahwa topik ini, meskipun mendasar, jauh dari dipahami oleh semua orang pertama kali, dan terlebih lagi, ada beberapa pertanyaan yang tidak jelas dalam bacaan pertama. Selain itu, akan terlihat bahwa pada hal-hal dasar seperti itu mereka masih menerbitkan artikel di IEEE dan ini masih jauh dari dilakukan oleh siswa . Kenapa tepatnya CubeSat? Masih lebih sederhana di sini: format satelit menarik (fakta keberadaan mikro dan nanosatellites, ternyata, membuat banyak orang terkejut), dan karenanya sangat cocok untuk keperluan pendidikan.

Simulasi akan dilakukan dalam python 3 untuk alasan yang sama seperti yang saya ungkapkan dalam publikasi saya sebelumnya . Kami akan mempertimbangkan case orbit rendah (LEO - Low Earth Orbit), dan menghitung, pada kenyataannya, rasio signal-to-noise (SNR - Signal-to-Noise ratio) pada input penerima melalui downlink (DL - Down Link). Kami akan menggunakan beberapa direktori dari akses terbuka dan membuat grafik untuk kejelasan.

Semua kode sumber tersedia di repositori GitHub saya, saya mengundang semua orang yang tertarik untuk membacanya! Saya akan sangat berterima kasih atas ulasan kode dan kritik yang membangun!

Ayo pergi!

Rumus apa yang akan kita hitung?

Pertama, tentu saja, ini adalah formula yang terkenal untuk rasio signal-to-noise pada skala logaritmik (dalam desibel, sederhana) untuk semua orang (yang terlibat dalam subjek), di mana kami memperhitungkan semua kemungkinan kerugian dan amplifikasi dengan sejumlah abstraksi:

$SNR = P_t + G_t + G_r + \ eta_ {t} + \ eta_ {r} - L_r - L_t - L - L_ {add} - N [dB] \ qquad (1)$

dimana - daya total noise termal (diketahui memiliki hubungan dengan kerapatan spektral noise) $N_0 = kT_ {noise}$ ) dalam dBm (desibel per miliwatt), P_t - Daya yang ditransmisikan dalam dBm, G_t dan G_r - penguatan antena di sisi pemancar dan penerima, masing-masing (dalam dBi - desibel isotropik), $\ eta_ {t}$ dan $\ eta_ {r}$ - gain dari pemancar dan penerima feeder (dalam dB), L_t dan L_r - kerugian pada pengumpan (dalam dB), kerugian di jalur rambat gelombang elektromagnetik di dB, $L_ {add}$ - tambahan kerugian (bisa dikatakan, beberapa margin) dalam dB.

Secara umum, dengan tujuh istilah pertama lebih atau kurang jelas: ini adalah data referensi. Hal-hal lebih menarik dengan tiga peserta terakhir dalam proses.

Daya derau termal

Seperti yang Anda ketahui, tidak ada tempat untuk bersembunyi dari momok perangkat elektronik ini, Anda hanya dapat mempertimbangkan:

$N = 10lg \ kiri (\ frac {kT_ {noise} B_ {noise}} {10 ^ {- 3}} \ kanan) [dBm] \ qquad (2)$

dimana - Konstanta Boltzmann $T_ {noise} = T_a + T_e$ - suhu kebisingan yang setara, T_a - jumlah kerugian antena dan kebisingan (latar belakang) dari langit, $T_e = T_0 (F_ {sys} -1)$ - suhu derau penerima ( T_0 = 290K , dan $F_ {sys} = 10 ^ {\ frac {NF} {10}}$ - Angka kebisingan, yang dapat diperkirakan dari gambar kebisingan ( - noise figure) dari antena penerima), dan $B_ {noise}$ - lebar pita frekuensi kebisingan. Anda dapat mengambil band noise sama dengan bandwidth dari receiver itu sendiri namun, menurut [1, hlm. 98] bandwidth noise $B_ {noise}$ dapat dinilai sedikit lebih akurat $\ gamma B$ dimana $\ gamma$ - konstan dari 1,002 ke 1,57 (berkaitan dengan konfigurasi penerima).

Kerugian tambahan

Di sini Anda dapat mengambil beberapa jenis pasokan yang dijamin, diperoleh, sebagai aturan, dari direktori yang sama, atau masuk lebih dalam dan menghitung semuanya sendiri.

Pada bagian ini, saya hampir sepenuhnya mengandalkan buku teks Cantor tua yang baik, yaitu bagian ini [1, hal. 88-96]. Jika pembaca memiliki sumber otoritatif yang lebih relevan - silakan bagikan, saya pikir ini akan bermanfaat bagi semua orang.

Apa yang terutama kami perhatikan:

Kehilangan karena pembiasan dan ketidaktepatan menunjuk antena ( Antenna Beam Loss )

Ditunjuk sebagai $L_b = 10log_ {10} (1+ (2 \ theta / \ theta_ {0,5}) ^ 2)$ dimana $\ theta$ - lebar balok dan $\ theta_ {0,5}$ - lebar balok setengah daya, dan tergantung, tidak peduli seberapa sulit untuk menebak, pada karakteristik perangkat antena tertentu:

Efek fase atmosfer

Jika Anda meyakini hal klasik, maka kerugian ini terutama memengaruhi kecepatan transfer data karena bandwidth penerima, karena itu disarankan untuk memilih pita sesuai dengan tabel 1 [1, hal. 91]. Untuk menghindari distorsi fase.

Tab. 1. Bandwidth penerima maksimum untuk rentang yang berbeda.

Frekuensi Pembawa, GHz	0,5	1	5	10
Bandwidth penerima (B), MHz	10	25	270	750

Meskipun, perlu dicatat bahwa angka-angka tersebut sangat mengesankan dan seringkali tidak dipertimbangkan, lebih karena kebisingan termal.

Kerugian karena ketidakcocokan antena polarisasi

Dapat diperkirakan tergantung pada koefisien ellipticity $e_1$ dan $e_2$ (Saya melampirkan kliping dari buku Soviet seperti Gambar 1).

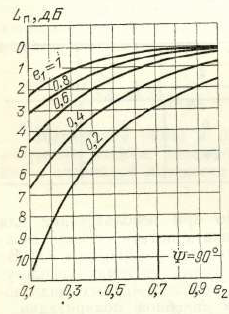
Fig. 1. Ketergantungan kerugian karena ketidakcocokan polarisasi antara antena pengirim dan penerima pada eliptisitas. [1, hlm. 93]

Namun, saya menemukan parameter ini sebagai referensi. Misalnya, dalam menghitung anggaran energi untuk NanoCom AX100, kerugian polarisasi adalah 3 dB (kehilangan atmosfer 2.1 dB, rugi ionosfer adalah 0.4 dB).

Atenuasi atmosfer

Kami dapat mengevaluasi parameter yang menarik ini sesuai dengan rekomendasi ITU , atau menghitungnya sendiri. Untungnya, ada perpustakaan khusus seperti ini .

Atenuasi di sepanjang jalur rambat gelombang elektromagnetik (Path Loss)

Tanpa basa-basi lagi, kami menerapkan rumus Friis untuk memulai dengan :

$L = 20lg \ frac {\ lambda} {4 \ pi d} [dB] \ qquad (3)$

dimana $\ lambda$ - panjang gelombang elektromagnetik (berhubungan dengan cara yang diketahui dengan frekuensi pembawa $f_0 = \ frac {c} {\ lambda}$ , Apakah kecepatan gelombang elektromagnetik (kecepatan cahaya, jika lebih sederhana)), dan - Jarak antara satelit dan stasiun bumi.

Dan di sini kita sampai pada pertanyaan yang paling menarik: jarak berapa yang harus kita ambil untuk perhitungan? Seperti yang telah disebutkan dalam pendahuluan, kami mempertimbangkan satelit LEO, yang berarti bahwa dugaan satelit kami bergerak relatif terhadap Bumi (berbeda dengan kasus geostasioner, di mana satelit, seolah-olah, tergantung pada satu titik).

Anda dapat, tentu saja, menyederhanakan segala sesuatu sebanyak mungkin dengan mengambil skema sebagai basis (Gbr. 2), ketika diasumsikan bahwa orbit satelit komunikasi terletak, secara kasar, "di atas kepala" stasiun darat kami.

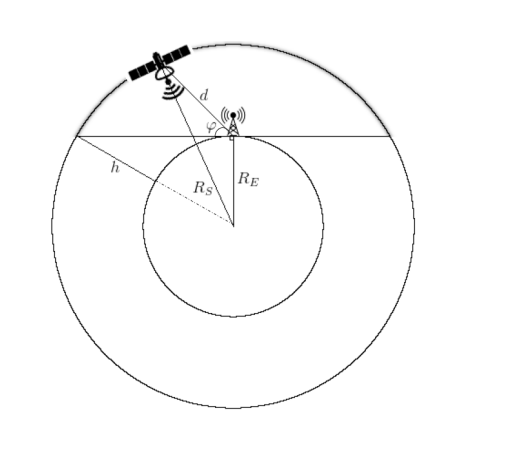
Fig. 2. Deskripsi skematik lintasan CubeSat di orbit Bumi rendah [2].

Maka jarak dapat dihitung dengan rumus:

$d = \ sqrt {(R_E + h) ^ 2-R_E ^ 2cos ^ 2 \ phi} - R_Esin \ phi \ qquad (4)$

dimana R_E - Sebenarnya, ada jari-jari Bumi, - ketinggian orbit satelit, dan $\ phi$ - sudut ketinggian.

Namun, Anda dapat menambahkan sedikit lebih banyak, kembali ke klasik (sudah berbeda) [3, hal.110-123] dan menghitung semuanya sudah relatif terhadap koordinat geografis nyata dari stasiun bumi (
$lat_ {gs}$ dan $long_ {gs}$ ) dan posisi sebenarnya dari satelit (node ascending instan - $L_ {simpul}$ dan kutub orbit - kutub orbit sesaat saya ) Bersiaplah, akan ada banyak trigonometri:

$d_ {min} = R_E \ frac {\ sin \ lambda_ {min}} {\ sin \ eta_ {min}} \ qquad (5)$

dimana $\ sin \ lambda_ {min} = \ sin (90 ^ 0 - i) \ sin (lat_ {gs}) + \ cos (90 ^ 0 - i) \ cos (lat_ {gs}) \ cos (long_ {gs} - (L_ {node} - 90 ^ 0))$ - sudut tengah minimum Bumi, $\ eta_ {min} = arctan \ frac {\ sin \ rho \ sin \ lambda_ {min}} {1 - \ sin \ rho \ cos \ lambda_ {min}}$ - sudut nadir minimum, $\ rho = arcsin \ frac {R_E} {R_E + h}$ Adalah jari-jari sudut Bumi. Jarak maksimum dapat dihitung dengan:

$d_ {max} = R_E \ frac {\ sin \ lambda_ {max}} {\ sin \ eta_ {max}} \ qquad (6)$

dimana $\ sin \ eta_ {max} = \ sin \ rho \ cos \ epsilon_ {min}$ dan $\ lambda_ {max} = 90 ^ 0 - \ epsilon_ {min} - \ eta_ {max}$ ( $\ epsilon_ {min}$ - sudut ketinggian minimum satelit).

Untuk meringkas ringkasan pendek dari parameter :

Apa yang kita pilih sebagai titik awal : frekuensi pembawa, ketinggian orbit (mungkin posisi satelit dan koordinat geografis dari stasiun darat - tergantung pada keakuratan yang ingin kita dapatkan);
Kami menemukan parameter yang bergantung pada peralatan dan dapat disesuaikan : daya yang ditransmisikan, bandwidth penerima;
Kami menemukan data referensi : gain dan loss antena, gain dan loss feeder, suhu kebisingan, kehilangan tambahan.

Kami mensimulasikan apa yang terjadi sebagai hasilnya

Sebagai sumber parameter teknis untuk penilaian downlink, kami memiliki contoh transceiver dan antena nyata untuk satelit CubeSat, seperti NanoCom AX100 dan NanoCom ANT430 . Untuk bandwidth yang lebih besar, tentu saja lebih baik untuk mempertimbangkan S-band . Antena patch NanoCom ANT2000 dan transceiver NanoCom SR2000 tersedia untuk kisaran ini.

Kami mulai memeriksa apa yang terjadi.

from SmallSatLB import * import pandas as pd

Semua logika secara kondisional dibagi menjadi dua opsi: 'draft' , di mana rumus (4) digunakan untuk menghitung jarak; dan 'tepat' , di mana rumus (5) dan (6) digunakan.

'draft'

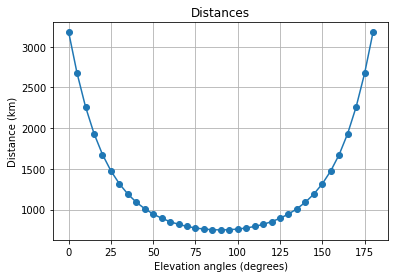
 l_d = LinkBudget(750*1e3, 'draft') #   (   ) d = l_d.distance() #   phi = np.pi*np.array(range(0,181,5))/180 #     plt.plot(180*phi/np.pi, d*1e-3, '-o') plt.title('Distances') plt.xlabel('Elevation angles (degrees)') plt.ylabel('Distance (km)') plt.grid()

 snr, EIRP = l_d.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) #  SNR plt.title('Expected SNRs') plt.xlabel('Elevation angles (degrees)') plt.ylabel('SNR (dB)') plt.legend() plt.grid()

Cantik!

'tepat'

 l_p = LinkBudget(750*1e3, 'precise',\ L_node = 100+90, incl = 90 - 61.5,\ lat_gs = 22, long_gs = 200, eps_min = 5) snr, EIRP = l_p.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) print(min(snr)) print(max(snr))

 >>> 5.556823874020452 >>> 8.667000351847676

Secara umum, di sini: kami memiliki alat kecil untuk "perkiraan" primer dan perhitungan berapa banyak sinyal akan melemah, sementara itu bergerak dari satelit ke Bumi (atau sebaliknya).
Terima kasih atas perhatian Anda!

Daftar literatur yang digunakan :

Kantor L. Ya., Askinazi G.B. Komunikasi dan penyiaran satelit: buku referensi . - Radio dan komunikasi, 1988.
Otilia Popescuy, Jason S. Harrisz dan Dimitrie C. Popescuz, Merancang Sub-Sistem Komunikasi untuk Nanosatellite CubeSat Misi: Perspektif Operasional dan Implementasi, 2016, IEEE
Wertz JR, Larson WJ Analisis dan Desain Misi Ruang Angkasa, Perpustakaan Teknologi Ruang Angkasa - Microcosm Press dan Penerbit Akademik Kluwer, El Segundo, CA, USA ,, 1999.

Kami menghitung anggaran energi saluran radio untuk satelit format CubeSat