Selamat Hari Kosmonautika! Kami menyerahkan kepada sebuah percetakan sebuah
buku kecil tentang lubang hitam . Pada hari-hari inilah ahli astrofisika menunjukkan kepada seluruh dunia bagaimana lubang hitam terlihat. Kebetulan? Kami tidak berpikir;) Jadi tunggu sebentar, sebuah buku yang luar biasa akan muncul, ditulis oleh Stephen Gabser dan Frans Pretorius, diterjemahkan oleh astronom Pulkovo yang luar biasa alias Astroded Kirill Maslennikov, sang legendaris Vladimir Surdin membuat pengeditan ilmiah dan Yayasan Trajektori mendukung penerbitannya.
Kutipan "Termodinamika lubang hitam" di bawah luka.
Sampai sekarang, kita telah menganggap lubang hitam sebagai objek astrofisika yang terbentuk selama ledakan supernova atau terletak di pusat galaksi. Kami mengamati mereka secara tidak langsung, mengukur percepatan bintang yang dekat dengannya. Registrasi gelombang gravitasi yang terkenal oleh penerima LIGO pada 14 September 2015 menjadi contoh pengamatan langsung dari tabrakan lubang hitam. Alat matematika yang kami gunakan untuk mendapatkan pemahaman yang lebih baik tentang sifat lubang hitam adalah: geometri diferensial, persamaan Einstein dan metode analitik dan numerik yang kuat yang digunakan untuk menyelesaikan persamaan Einstein dan untuk menggambarkan geometri ruang-waktu yang dihasilkan lubang hitam. Dan segera setelah kami dapat memberikan deskripsi kuantitatif penuh ruang-waktu yang dihasilkan oleh lubang hitam, dari sudut pandang astrofisika topik lubang hitam dapat dianggap tertutup. Dalam perspektif teoretis yang lebih luas, masih ada banyak peluang untuk penelitian. Tujuan bab ini adalah untuk berbicara tentang beberapa pencapaian teoritis fisika lubang hitam modern, di mana ide-ide termodinamika dan teori kuantum dikombinasikan dengan teori relativitas umum, sehingga memunculkan konsep baru yang tidak terduga. Ide dasarnya adalah bahwa lubang hitam bukan hanya benda geometris. Mereka memiliki suhu, mereka memiliki entropi yang sangat besar dan dapat menunjukkan manifestasi keterikatan kuantum. Diskusi kita tentang aspek termodinamika dan kuantum dari fisika lubang hitam akan lebih samar dan dangkal daripada analisis fitur ruang-waktu murni geometris dalam lubang hitam yang disajikan dalam bab-bab sebelumnya. Tetapi aspek-aspek ini, dan terutama kuantum, adalah bagian penting dan vital dari studi teoritis lubang hitam yang sedang berlangsung, dan kami akan berusaha sangat keras untuk menyampaikan, jika bukan detail yang rumit, maka setidaknya semangat dari karya-karya ini.
Dalam teori relativitas umum klasik - jika kita berbicara tentang geometri diferensial dari solusi persamaan Einstein - lubang hitam benar-benar hitam dalam arti tidak ada yang bisa keluar darinya. Stephen Hawking menunjukkan bahwa situasi ini benar-benar berubah ketika kita memperhitungkan efek-efek kuantum: lubang hitam ternyata memancarkan radiasi suhu tertentu, yang dikenal sebagai suhu Hawking. Untuk lubang hitam dengan ukuran astrofisika (mis., Dari lubang hitam massa bintang hingga supermasif), suhu Hawking dapat diabaikan dibandingkan dengan suhu latar belakang gelombang mikro kosmik - radiasi mengisi seluruh Semesta, yang, dengan cara lain, dapat dengan sendirinya dianggap sebagai varian dari radiasi Hawking. Perhitungan yang dilakukan oleh Hawking untuk menentukan suhu lubang hitam adalah bagian dari program penelitian yang lebih luas di bidang yang disebut termodinamika lubang hitam. Bagian utama lain dari program ini adalah studi tentang entropi lubang hitam, yang mencirikan jumlah informasi yang hilang di dalam lubang hitam. Benda-benda biasa (seperti cangkir air, sebatang magnesium murni atau bintang) juga memiliki entropi, dan salah satu pernyataan sentral dari termodinamika lubang hitam adalah bahwa lubang hitam dengan ukuran ini memiliki lebih banyak entropi daripada bentuk benda apa pun yang dapat ditampung dalam area dengan ukuran yang sama, tetapi tanpa pembentukan lubang hitam.
Tetapi sebelum kita terjun jauh ke dalam diskusi tentang masalah yang terkait dengan radiasi Hawking dan entropi lubang hitam, mari kita bertamasya cepat ke bidang mekanika kuantum, termodinamika, dan keterikatan. Mekanika kuantum dikembangkan terutama pada tahun 1920-an, dan tujuan utamanya adalah untuk mendeskripsikan partikel materi yang sangat kecil, seperti atom. Perkembangan mekanika kuantum menyebabkan erosi konsep-konsep dasar fisika seperti posisi persis partikel individu: ternyata, misalnya, posisi elektron ketika bergerak di sekitar inti atom tidak dapat ditentukan secara tepat. Alih-alih, yang disebut orbit ditugaskan ke elektron, di mana posisi aktual mereka hanya dapat ditentukan dalam arti probabilistik. Namun, untuk tujuan kita, penting untuk tidak beralih ke sisi - probabilitas - hal-hal ini terlalu cepat. Ambil contoh paling sederhana: atom hidrogen. Itu bisa dalam keadaan kuantum tertentu. Keadaan paling sederhana dari atom hidrogen, yang disebut keadaan dasar, adalah keadaan dengan energi terendah, dan energi ini diketahui dengan tepat. Dalam pengertian yang lebih umum, mekanika kuantum memungkinkan kita (secara prinsip) untuk mengetahui keadaan sistem kuantum apa pun secara akurat.
Peluang muncul ketika kita mengajukan pertanyaan tertentu tentang sistem mekanika kuantum. Sebagai contoh, jika diketahui bahwa atom hidrogen berada dalam kondisi dasar, kita dapat bertanya: "Di mana elektron?" dan menurut hukum kuantum
mekanika kita sampai pada pertanyaan ini hanya perkiraan probabilitas tertentu, kira-kira seperti: "elektron mungkin terletak pada jarak hingga setengah angstrom dari inti atom hidrogen" (satu angstrom sama dengan
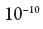
meter). Tetapi kita memiliki kesempatan, melalui proses fisik tertentu, untuk menemukan posisi elektron jauh lebih akurat daripada satu angstrom. Proses ini, yang cukup umum dalam fisika, terdiri dari peluncuran foton dengan panjang gelombang yang sangat pendek ke dalam elektron (atau, seperti dikatakan oleh fisikawan, menyebarkan foton pada elektron) - setelah itu kita dapat merekonstruksi lokasi elektron pada saat hamburan dengan akurasi yang kira-kira sama dengan panjang gelombang. foton. Tetapi proses ini akan mengubah keadaan elektron, sehingga setelah itu ia tidak akan lagi berada di keadaan dasar atom hidrogen dan tidak akan memiliki energi yang ditentukan secara tepat. Tetapi untuk beberapa waktu posisinya akan hampir pasti ditentukan (akurat untuk panjang gelombang foton yang digunakan untuk ini). Penilaian awal dari posisi elektron dapat dilakukan hanya dalam arti probabilistik dengan akurasi sekitar satu angstrom, tetapi segera setelah kami mengukurnya, kami tahu persis apa itu setara dengan. Singkatnya, jika kita mengukur sistem mekanika kuantum dalam beberapa cara, maka, setidaknya dalam pengertian yang diterima secara umum, kita "secara paksa" memberinya status dengan nilai tertentu dari jumlah yang kita ukur.
Mekanika kuantum berlaku tidak hanya untuk yang kecil, tetapi (seperti yang kami yakini) untuk semua sistem, tetapi untuk sistem yang besar, aturan mekanika kuantum dengan cepat menjadi sangat kompleks. Konsep kuncinya adalah keterikatan kuantum, contoh sederhana di antaranya adalah konsep putaran (rotasi). Elektron individu memiliki putaran, sehingga dalam praktiknya satu elektron dapat memiliki putaran yang diarahkan ke atas atau ke bawah sehubungan dengan sumbu spasial yang dipilih. Putaran elektron adalah jumlah yang diamati, karena elektron menghasilkan medan magnet yang lemah, mirip dengan bidang batang magnet. Kemudian spin menunjuk ke atas berarti kutub utara elektron menunjuk ke bawah, dan spin menunjuk ke bawah berarti kutub utara "melihat ke atas". Dua elektron dapat dimasukkan ke dalam keadaan kuantum terkonjugasi, di mana salah satu dari mereka memiliki putaran mengarah ke atas dan yang lainnya ke bawah, tetapi tidak mungkin untuk mengatakan elektron mana yang memiliki putaran mana. Faktanya, dalam keadaan dasar atom helium, dua elektron berada dalam kondisi yang persis sama, disebut spin-singlet, karena putaran total kedua elektron sama dengan nol. Jika kita memisahkan kedua elektron ini tanpa mengubah putarannya, kita dapat terus mengklaim bahwa keduanya adalah spin-singlet bersama-sama, tetapi kita masih tidak dapat mengatakan seperti apa masing-masing spin itu secara individual. Sekarang, jika kita mengukur salah satu putaran mereka dan memastikan bahwa itu diarahkan ke atas, maka kita akan sepenuhnya yakin bahwa yang kedua diarahkan ke bawah. Dalam situasi ini, kami mengatakan bahwa punggung terjerat - tidak satu pun dalam dirinya sendiri memiliki makna yang pasti, sementara bersama-sama mereka berada dalam keadaan kuantum yang pasti.
Einstein sangat prihatin dengan fenomena keterikatan: tampaknya mengancam prinsip-prinsip dasar teori relativitas. Mari kita perhatikan kasus dua elektron dalam keadaan spin-singlet, ketika mereka jauh dari satu sama lain di ruang angkasa. Untuk jelasnya, biarkan salah satu dari mereka mengambil Alice dan Bob lainnya. Misalkan Alice mengukur putaran elektronnya dan mendapati bahwa elektronnya naik, dan Bob tidak mengukur apa pun. Sampai Alice menyelesaikan pengukurannya, tidak mungkin untuk mengetahui berapa putaran elektronnya. Tetapi begitu dia menyelesaikan pengukurannya, dia benar-benar tahu bahwa putaran elektron Bob diarahkan ke bawah (ke arah yang berlawanan dengan putaran elektronnya sendiri). Apakah ini berarti bahwa pengukurannya secara instan mentransfer elektron Bob ke keadaan ketika putarannya diarahkan ke bawah? Bagaimana ini bisa terjadi jika elektron dipisahkan secara spasial? Einstein dan rekan kerjanya Nathan Rosen dan Boris Podolsky merasa bahwa kisah pengukuran sistem yang terjerat sangat serius sehingga mengancam keberadaan mekanika kuantum. Paradoks Einstein - Podolsky - Rosen (EPR) yang dirumuskan oleh mereka menggunakan eksperimen pemikiran yang mirip dengan yang baru saja kita gambarkan untuk menyimpulkan: mekanika kuantum tidak dapat menjadi deskripsi lengkap tentang kenyataan. Sekarang, berdasarkan penelitian teoritis yang mengikuti, dan banyak pengukuran, pendapat umum telah ditetapkan bahwa paradoks EPR mengandung kesalahan, dan teori kuantum benar. Keterikatan kuantum-mekanis adalah nyata: pengukuran sistem yang terjerat akan berkorelasi, bahkan jika sistem ini terpisah jauh dalam ruang-waktu.
Mari kita kembali ke situasi di mana kita menempatkan dua elektron dalam keadaan spin-singlet dan membagikannya kepada Alice dan Bob. Apa yang bisa kita katakan tentang elektron sebelum pengukuran dilakukan? Bahwa keduanya bersama-sama mereka berada dalam keadaan kuantum tertentu (spin-singlet). Perputaran elektron Alicin sama-sama cenderung diarahkan ke atas atau ke bawah. Lebih tepatnya, keadaan kuantum elektronnya dengan probabilitas yang sama dapat berupa satu (spin up) atau lainnya (spin down). Sekarang bagi kami konsep probabilitas mengambil makna yang lebih dalam dari sebelumnya. Sebelumnya, kami mempertimbangkan keadaan kuantum tertentu (keadaan dasar atom hidrogen) dan melihat bahwa ada beberapa pertanyaan "tidak nyaman", seperti, "Di mana elektron berada?", Pertanyaan yang jawabannya hanya ada dalam arti probabilistik. Jika kita mengajukan pertanyaan "baik", misalnya: "Apa energi elektron ini?", Kami akan mendapatkan jawaban tertentu untuk mereka. Sekarang tidak ada pertanyaan "baik" yang bisa kami tanyakan tentang elektron Alice, jawaban yang tidak akan bergantung pada elektron Bob. (Kami tidak berbicara tentang pertanyaan bodoh seperti "Apakah elektron Alice memiliki putaran sama sekali?" - pertanyaan yang hanya ada satu jawaban.) Jadi, kita harus menggunakan bahasa probabilistik untuk menentukan parameter dari salah satu sistem yang setengah bingung. Kepastian muncul hanya ketika kita mempertimbangkan hubungan antara pertanyaan yang dapat ditanyakan Alice dan Bob tentang elektronnya.
Kami sengaja memulai dengan salah satu sistem mekanika kuantum paling sederhana yang kami ketahui: sistem spin elektron individu. Diharapkan bahwa komputer kuantum akan dibangun berdasarkan sistem sederhana tersebut. Sistem spin elektron individu atau sistem kuantum setara lainnya sekarang disebut qubit (kependekan dari "bit kuantum"), yang menekankan perannya dalam komputer kuantum, mirip dengan peran yang dimainkan oleh bit biasa dalam komputer digital.
Bayangkan sekarang bahwa kita telah mengganti setiap elektron dengan sistem kuantum yang jauh lebih kompleks dengan banyak, dan bukan hanya dua keadaan kuantum. Misalnya, mereka memberi Alice dan Bob batang magnesium murni. Sebelum Alice dan Bob berpisah dengan arah yang berbeda, bar mereka dapat berinteraksi, dan kami akan setuju bahwa dengan melakukan itu mereka memperoleh keadaan kuantum umum tertentu. Begitu Alice dan Bob berpisah, batang magnesium mereka berhenti berinteraksi. Seperti dalam kasus elektron, setiap batang berada dalam keadaan kuantum tidak terbatas, meskipun bersama-sama, seperti yang kami yakini, mereka membentuk keadaan yang sepenuhnya pasti. (Dalam diskusi ini, kita mengasumsikan bahwa Alice dan Bob dapat memindahkan batang magnesium mereka tanpa mengganggu keadaan internal mereka, seperti yang kita asumsikan sebelumnya bahwa Alice dan Bob dapat memisahkan elektron mereka yang terjerat tanpa mengubah putaran mereka.) Tetapi perbedaannya antara eksperimen pemikiran ini dan eksperimen dengan elektron adalah bahwa ketidakpastian dalam keadaan kuantum setiap batang sangat besar. Sebuah bar mungkin memperoleh lebih banyak status kuantum daripada jumlah atom di alam semesta. Di sinilah termodinamika memasuki panggung. Namun, sistem yang sangat tidak akurat dapat memiliki beberapa karakteristik makroskopis yang terdefinisi dengan baik. Karakteristik seperti itu, misalnya, suhu. Suhu adalah ukuran dari probabilitas di mana setiap bagian dari sistem memiliki energi rata-rata tertentu, dengan suhu yang lebih tinggi sesuai dengan probabilitas lebih tinggi untuk memiliki lebih banyak energi. Parameter termodinamika lain adalah entropi, yang pada dasarnya sama dengan logaritma dari sejumlah status yang dapat diambil oleh sistem. Karakteristik termodinamika lain yang akan signifikan untuk sebatang magnesium adalah total magnetisasi, yaitu, pada dasarnya, parameter yang menunjukkan berapa banyak elektron dapat berada di bar dengan putaran yang mengarah ke atas daripada dengan putaran yang mengarah ke bawah.
Kami telah melibatkan termodinamika dalam cerita kami sebagai cara untuk menggambarkan sistem yang status kuantumnya tidak diketahui karena keterkaitannya dengan sistem lain. Termodinamika adalah alat yang ampuh untuk menganalisis sistem seperti itu, tetapi penciptanya sama sekali tidak mengharapkan aplikasi seperti itu. Sadi Carnot, James Joule, Rudolph Clausius adalah pemimpin revolusi industri abad XIX, dan tertarik pada pertanyaan paling praktis dari semua pertanyaan mereka: bagaimana cara kerja mesin? Tekanan, volume, suhu, dan panas adalah daging dan darah mesin. Carnot menemukan bahwa energi dalam bentuk panas tidak akan pernah dapat sepenuhnya berubah menjadi pekerjaan yang bermanfaat seperti mengangkat barang. Sebagian energi akan selalu terbuang sia-sia. Clausius membuat kontribusi utama pada penciptaan ide entropi sebagai alat universal untuk menentukan kehilangan energi selama proses yang terkait dengan panas. Prestasi utamanya adalah kesadaran bahwa entropi tidak pernah berkurang - dalam hampir semua proses itu tumbuh. Proses di mana peningkatan entropi disebut ireversibel - justru karena mereka tidak dapat membalikkan tanpa mengurangi entropi. Langkah selanjutnya dalam pengembangan mekanika statistik dilakukan oleh Clausius, Maxwell dan Ludwig Boltzmann (di antara banyak lainnya) - mereka menunjukkan bahwa entropi adalah ukuran gangguan. Biasanya semakin Anda bertindak atas sesuatu, semakin Anda mengacaukannya. Dan bahkan jika Anda telah mengembangkan suatu proses yang tujuannya adalah memulihkan ketertiban, dalam perjalanannya lebih banyak entropi akan terbentuk daripada dihancurkan, misalnya, ketika panas dilepaskan. Crane, yang menumpuk balok baja dalam urutan yang sempurna, menciptakan keteraturan dalam hal lokasi balok, tetapi begitu banyak panas akan dilepaskan selama operasinya sehingga total entropi masih tumbuh.
Tapi tetap saja, perbedaan antara pandangan tentang termodinamika fisikawan abad ke-19 dan pandangan yang terkait dengan keterikatan kuantum tidak begitu besar seperti yang terlihat. Setiap kali suatu sistem berinteraksi dengan agen eksternal, keadaan kuantumnya menjadi bingung dengan keadaan kuantum agen. Biasanya keterjeratan ini mengarah pada peningkatan ketidakpastian kondisi kuantum sistem, dengan kata lain, peningkatan jumlah keadaan kuantum di mana sistem itu bisa. Sebagai hasil dari interaksi dengan sistem lain, entropi, yang didefinisikan dalam hal jumlah keadaan kuantum yang tersedia untuk sistem, biasanya tumbuh.
Secara umum, mekanika kuantum memberikan cara baru untuk mengkarakterisasi sistem fisik di mana beberapa parameter (mis., Posisi dalam ruang) menjadi tidak pasti, sementara yang lain (mis., Energi) sering diketahui dengan tepat. Dalam kasus keterikatan kuantum, dua bagian sistem yang secara fundamental terpisah memiliki keadaan kuantum umum yang diketahui, dan masing-masing bagian secara terpisah adalah keadaan tak terbatas. Contoh standar keterjeratan adalah sepasang putaran dalam keadaan singlet di mana tidak mungkin untuk mengatakan putaran mana yang diarahkan ke atas dan mana yang turun. , , , , .
, , , , . — , , , 2π. , , , ‑. , , , . : - ? , , , . , , 6 . , ( , ) . , 1,5 , . , , , , ; , , . , , . ( « , …», , , , .) , , : , , , , , , . , , , , , , , , . : ! , , , , , . , , , , , , . , -. , , - , .
, - , - . , , - : , . , , , , -, . , - , (, , , ). -, , , , , . - , . , 60 . , , ( ) ,
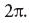
. 7.1. , a . , , t = 0. , t = 0 . , ‑.
, , « ». ? ? , . , , , . — , — , , . -, , ‑. - , , . , !
, , , — , , . «» , «», , , . 2, , , , . , , . , , ? , . , ? , , , . , , .