🆗 ♎️ 👷 Entropi Informasi Kekacauan 🍗 👙 🖤

Pendahuluan

Ada banyak publikasi tentang Habr yang membahas konsep entropi, berikut beberapa di antaranya [1 ÷ 5]. Publikasi diterima secara positif oleh pembaca dan membangkitkan minat besar. Cukup memberikan definisi entropi yang diberikan oleh penulis publikasi [1]: "entropi adalah seberapa banyak informasi yang tidak Anda ketahui tentang sistem." Publikasi tentang fenomena kekacauan pada Habr juga cukup [6-9]. Namun, hubungan entropi dan kekacauan di kedua kelompok publikasi tidak dipertimbangkan.

Hal ini disebabkan oleh fakta bahwa berbagai bidang pengetahuan membedakan berbagai jenis ukuran kekacauan:

informasi;
termodinamika;
diferensial;
budaya.

Tindakan kekacauan juga dijelaskan dengan mempertimbangkan kekhususannya, bahkan di salah satu bidang ini cukup sulit.

Berusaha menyederhanakan tugas semaksimal mungkin, saya memutuskan untuk mempertimbangkan hubungan antara entropi informasi dan kekacauan menggunakan contoh kesamaan daerah-daerah bagian dari urutan kekacauan di diagram dalam bentuk pemetaan titik dan pada grafik koefisien entropi untuk wilayah ini.

Apa yang datang dari ini, Anda akan belajar dengan melihat ke bawah kucing.

Mekanisme transisi dari tatanan ke kekacauan

Analisis mekanisme transisi dari kekacauan ke sistem nyata dan berbagai model telah mengungkapkan fleksibilitas dari beberapa skenario transisi ke kekacauan. Transisi menuju kekacauan dapat direpresentasikan dalam bentuk diagram bifurkasi (istilah “bifurkasi” digunakan untuk menunjukkan penataan ulang kualitatif sistem dengan munculnya mode baru dari perilakunya).

Masuknya sistem ke mode yang tidak dapat diprediksi dijelaskan oleh kaskade bifurkasi yang mengikuti satu demi satu. Kaskade bifurkasi mengarah secara berurutan ke pilihan antara dua solusi, kemudian empat dan seterusnya, sistem mulai berosilasi dalam mode kacau dan bergejolak yang secara berurutan menggandakan jumlah nilai yang mungkin.

Kami mempertimbangkan bifurkasi penggandaan periode dan munculnya kekacauan dalam pemetaan titik. Tampilan adalah fungsi yang menunjukkan ketergantungan dari nilai-nilai berikut dari parameter sistem pada nilai sebelumnya:

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Pertimbangkan juga fungsi kedua yang umum digunakan:

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Menggunakan pemetaan titik, objek dipelajari tidak dengan kontinu, tetapi dengan waktu diskrit . Setelah transisi ke tampilan, dimensi sistem yang sedang dipelajari dapat berkurang.

Ketika mengubah parameter eksternal \ lambda, pemetaan titik menunjukkan perilaku yang agak rumit, yang menjadi kacau dengan \ lambda yang cukup besar. Chaos adalah resesi lintasan yang sangat cepat di ruang fase.

Bifurkasi adalah restrukturisasi kualitatif film. Nilai parameter kontrol tempat terjadinya bifurkasi disebut nilai kritis atau bifurkasi.

Untuk membuat diagram, kami akan menggunakan dua daftar berikut:

1 Untuk fungsi:

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$

Daftar program

# -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=(a-1)/a#     def ff(x):#  return a*x*(1-x) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

2. Untuk fungsi

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Daftar program

 # -*- coding: utf8 -*- import matplotlib.pyplot as plt from numpy import * def f(a,x0): x1=((a-1)/a)**0.5 def ff(x):#  return a*x*(1-x**2) def fl(x): return x x=x0;y=0;Y=[];X=[] for i in arange(1,1000,1): X.append(x) Y.append(y) y=ff(x) X.append(x) Y.append(y) x=y plt.title('   \n\ $x_{n+1}=\lambda \cdot x_{n}\cdot (1-x_{n}^{2})$  $\lambda$ =%s  x0=%s '%(a,x0)) plt.plot(X,Y,'r') x1=arange(0,1,0.001) y1=[ff(x) for x in x1] y2=[fl(x) for x in x1] plt.plot(x1,y1,'b') plt.plot(x1,y2,'g') plt.grid(True) plt.show()

Untuk menilai dampak sifat fungsi logistik pada nilai kritis

$\ lambda$ pertimbangkan diagram dengan fungsi

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ Untuk melakukan ini, kami akan menggunakan daftar No. 1:

Untuk 0 <\ lambda <1 untuk

$\ lambda = $ 0,9$ dan x0 = 0,47 kita mendapatkan diagram:

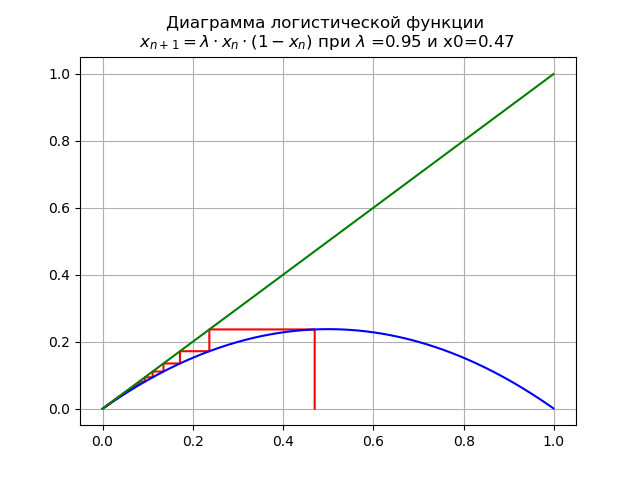
Dalam hal ini, peta memiliki titik tetap tunggal

$x ^ {*} = 0$
yang berkelanjutan.

Di

$1 <\ lambda <3$ untuk

$\ lambda = $ 2.$ x0 = 0,7 kita mendapatkan diagram:

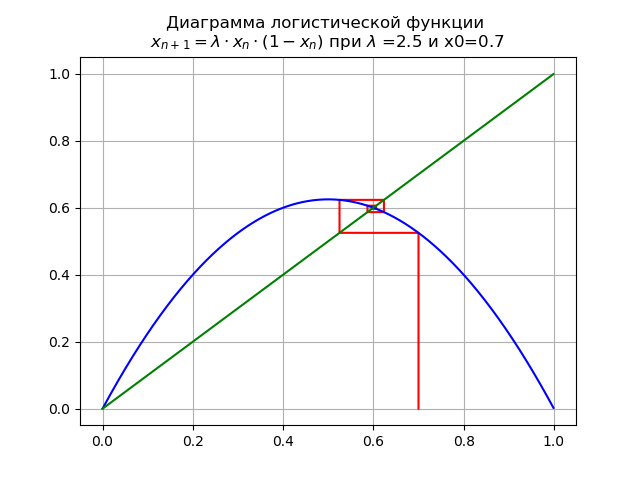
Pada segmen [0, 1], titik tetap tetap lainnya muncul

$x_ {1} ^ {*} = 1-1 / \ lambda$

Di

$1 <\ lambda <3$ untuk

$\ lambda = $ 2.$ dan x0 = 0,01 kita mendapatkan diagram:

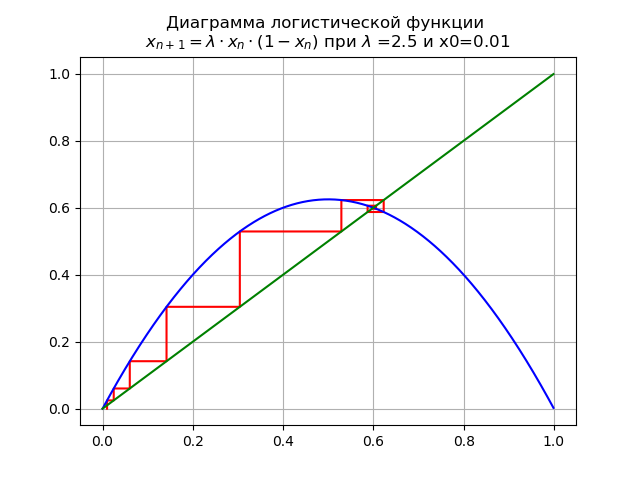
Titik tetap

$x ^ {*} = 0$ kehilangan stabilitas.

Di

$3 <\ lambda <3,45$ untuk

$\ lambda = $ 3,4$ dan x0 = 0,7 kita mendapatkan diagram:

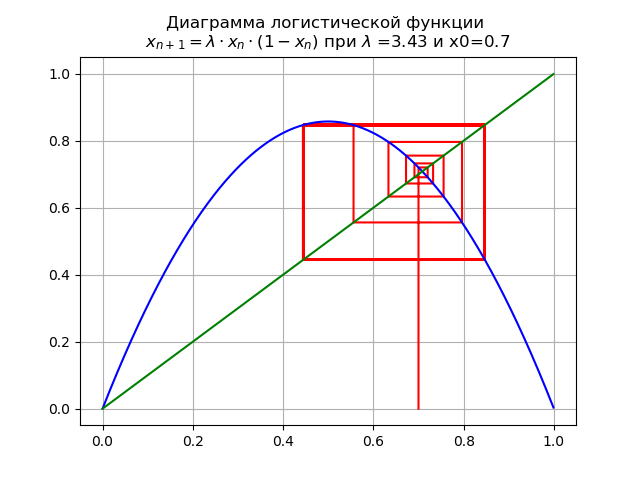
Pemetaan ini mengalami bifurkasi: titik tetap

$x_ {1} ^ {*}$ menjadi tidak stabil, dan siklus ganda muncul sebagai gantinya.

Di

$3,45 <\ lambda <4,0$ untuk

$\ lambda = $ 3.5$
dan x0 = 0,2 kita mendapatkan diagram:

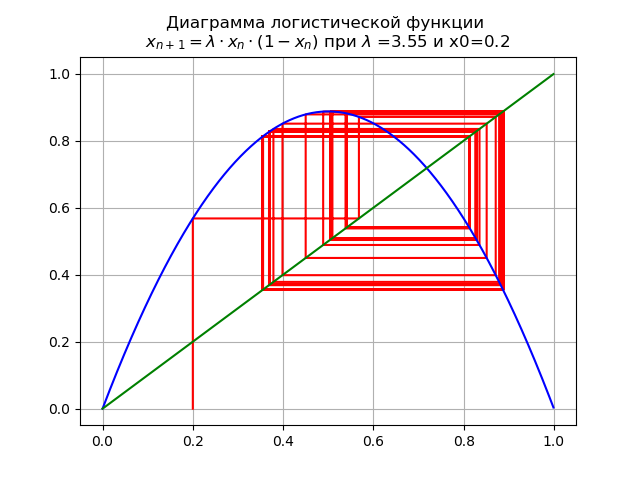
Saat melewati parameter

$\ lambda$ melalui nilai

$\ lambda = 3.45$ , Siklus 2 kali lipat menjadi 4 kali lipat, dan seterusnya.

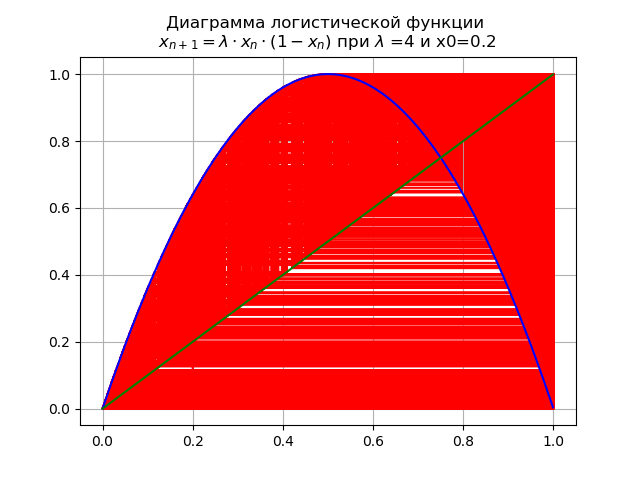
Pada nilai akhir

$\ lambda = 4$ sistem memiliki siklus tidak stabil dari semua pesanan yang mungkin:

Untuk menilai dampak sifat fungsi logistik pada nilai kritis

$\ lambda$ pertimbangkan diagram dengan fungsi

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ , untuk ini kita akan menggunakan daftar No. 2.

Di

$0 <\ lambda <= 1,0$ untuk

$\ lambda = 0,5$ dan x0 = 0,2:

Pemetaan memiliki satu titik tetap

$x ^ {*} = 0$ yang berkelanjutan.

Di

$1 <\ lambda <= 1.998 ...$ untuk

$\ lambda = $ 1,$ dan x0 = 0,55:

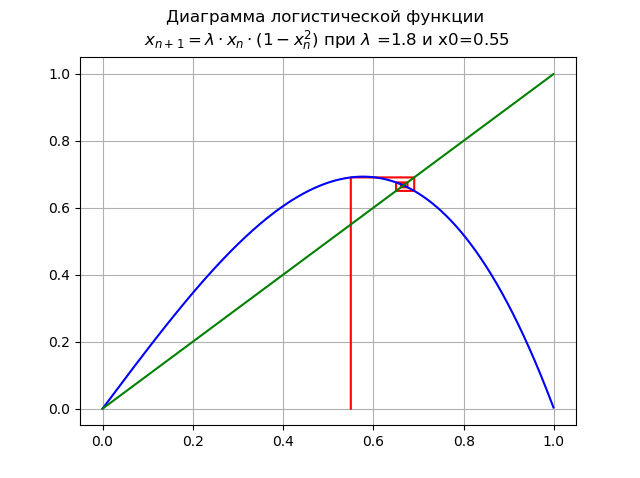
Point

$x ^ {*} = 0$ kehilangan stabilitas, titik stabil baru muncul

$x_ {1} ^ {*}$

Di

$1,99 <\ lambda <= 2,235 ...$ untuk

$\ lambda = $ 2.$ dan x0 = 0,2:

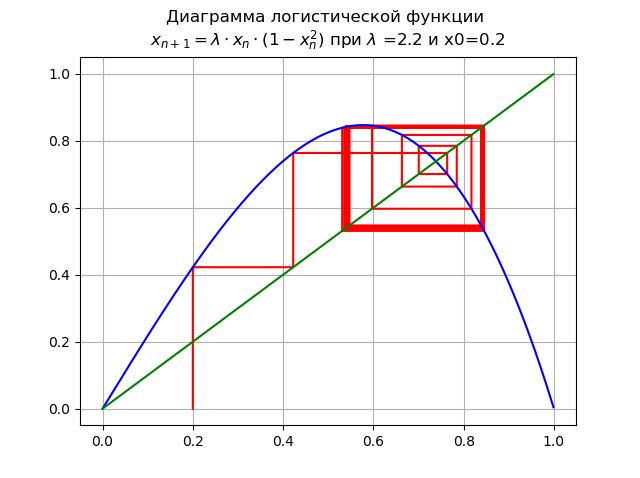
Bifurkasi dari penggandaan periode terjadi, siklus 2 kali lipat muncul. Peningkatan lebih lanjut

$\ lambda$ mengarah ke kaskade dua kali lipat bifurkasi.

Di

$2.235 <\ lambda 2.5980 ...$ untuk

$\ lambda = 2.287$ dan x0 = 0,2:

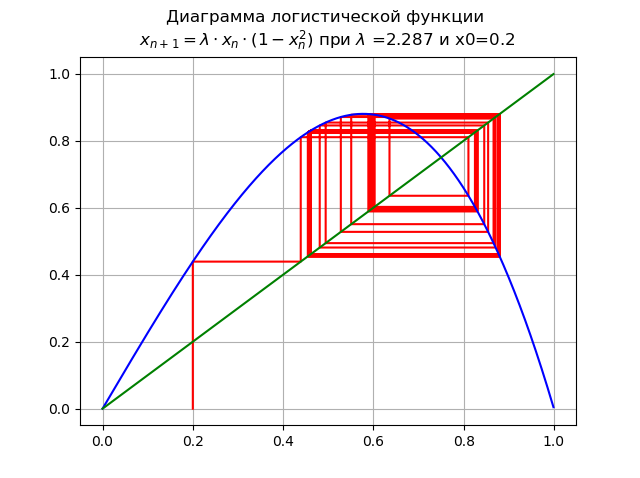
Meningkat

$\ lambda$ menyebabkan kaskade periode dua kali lipat bifurkasi.

Di

$\ lambda = 2.59$ sistem memiliki siklus tidak stabil dari semua periode yang memungkinkan:

Seperti yang ditunjukkan dalam diagram, dengan meningkatnya urutan fungsi logistik, rentang perubahan

$\ lambda$ berangsur-angsur berkurang.

Menggunakan diagram, kami melacak jalur dari urutan ke kekacauan, sambil mengatur nilai

$\ lambda$ untuk fungsi logistik yang berbeda. Tetap menjawab pertanyaan: bagaimana mengukur kekacauan? Jawaban untuk beberapa jenis kekacauan yang terdaftar di awal artikel diketahui
- Entropi adalah ukuran kekacauan. Jawaban ini dapat sepenuhnya dikaitkan dengan kekacauan informasi, bagaimanapun, entropi apa yang diterapkan di sini dan bagaimana membandingkan dengan nilai numerik yang sudah dipertimbangkan

$\ lambda$ - Saya akan mencoba menjawab pertanyaan ini di bagian artikel selanjutnya.

Entropi informasi dan koefisien entropi

Kami akan mempertimbangkan entropi biner informasi untuk peristiwa acak independen.

$x$ c

$n$ kemungkinan status didistribusikan dengan probabilitas

$p_ {i} (i = 1, .., n)$ . Entropi biner informasi dihitung dengan rumus:

$H (x) = - \ sum_ {i = 1} ^ {n} p_ {i} \ cdot log_ {2} (p_ {i})$

Nilai ini juga disebut entropi rata-rata pesan. Nilai

$H_ {i} = - log_ {2} (p_ {i})$ disebut entropi pribadi, hanya mencirikan negara ke- i . Dalam kasus umum, dasar logaritma dalam definisi entropi bisa lebih besar dari 1; pilihannya menentukan unit pengukuran entropi.

Kami akan menggunakan logaritma desimal di mana entropi dan informasi diukur dalam bit. Jumlah informasi dalam bit akan dihitung dengan benar ketika, misalnya, variabel

$X$ dan

$\ Delta$ akan diganti ke dalam ekspresi yang sesuai untuk entropi di mana pun, tetapi selalu dalam unit yang sama. Memang:

$q = H (x) -H (\ Delta) = log_ {10} \ kiri (X_ {2} -X_ {1} \ kanan) -log_ {10} (2 \ Delta) = log_ {10} (\ frac {X_ {2} -X_ {1}} {2 \ Delta})$

dimana X dan

$\ Delta$ harus dalam satuan yang sama.

Perkiraan nilai entropi dari variabel acak dari data eksperimen ditemukan dari histogram dari hubungan berikut:

$\ Delta_ {e} = \ frac {1} {2} e ^ {H (x)} = \ frac {d} {2} \ prod_ {i = 1} ^ {m} (\ frac {n} { n_ {i}}) ^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10} (n_ {i})$

dimana:

$d$ –Lebar dari setiap kolom histogram;

$m$ - jumlah kolom;

$n$ -jumlah total data;

$n_ {i}$ - jumlah data dalam

$i$ kolom itu.

Koefisien entropi ditentukan dari rasio:

$k_ {e} = \ frac {\ Delta_ {e}} {\ sigma}$

dimana:

$\ sigma$ - standar deviasi.

Entropi informasi sebagai ukuran kekacauan

Untuk menganalisis fenomena kekacauan informasi menggunakan koefisien entropi, pertama-tama kita buat diagram cabang untuk fungsi tersebut

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ dengan penerapan area transisi yang diperoleh selama pembangunan histogram:

Diagram cabang

 import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   3,6<= $\lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$\lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()

Kami mendapatkan:

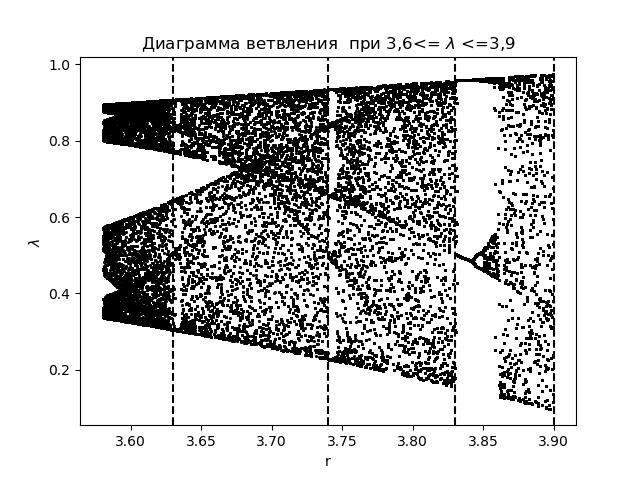
Kami merencanakan koefisien entropi untuk area yang sama

$\ lambda$ :

Grafik untuk koefisien entropi

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j]) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.title("  ke  3,6<= $\lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()

Kami mendapatkan:

Membandingkan diagram dan grafik, kita melihat tampilan yang identik dari daerah pada diagram dan pada grafik untuk koefisien entropi untuk fungsi

$x_ {n + 1} = f (x_ {n}) = \ lambda x_ {n} (1-x_ {n})$ .

Untuk analisis lebih lanjut tentang fenomena kekacauan informasi menggunakan koefisien entropi, kami membuat diagram cabang untuk fungsi logistik:

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$ dengan penerapan area transisi:

Diagram cabang

 import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-(y[n-1])**2),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title("   2.25<=$\lambda$ <=2.56") plt.xlabel("$\lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()

Kami mendapatkan:

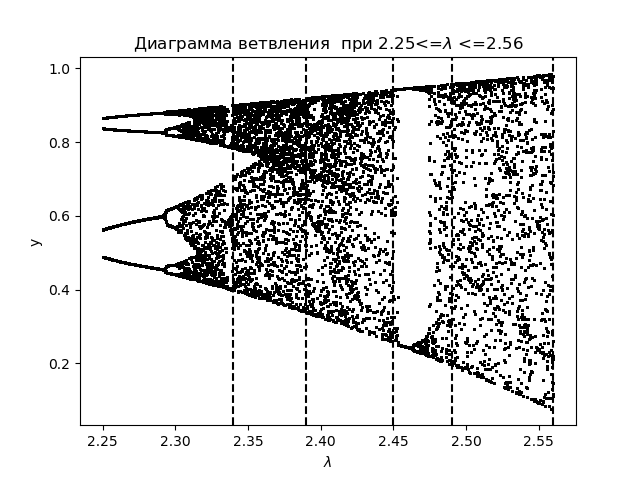
Kami merencanakan koefisien entropi untuk area yang sama

$\ lambda$ :

Grafik koefisien entropi

 import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.figure(2) plt.title("  ke  2.25<= $\lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()

Kami mendapatkan:

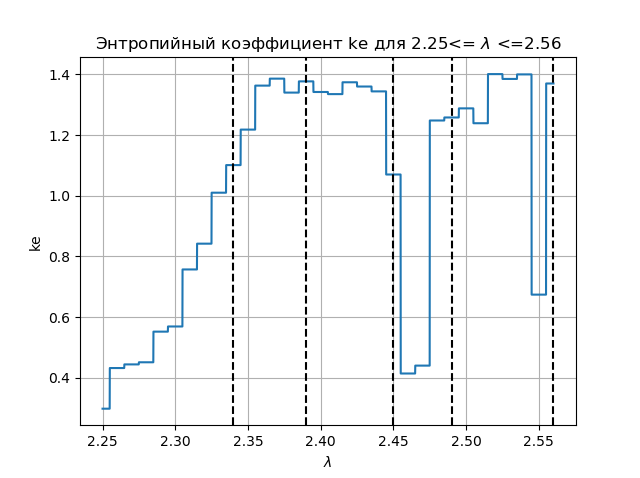
Membandingkan diagram dan grafik, kita melihat tampilan yang identik dari daerah pada diagram dan pada grafik untuk koefisien entropi untuk fungsi

$x_ {n + 1} = f (x_ {n}) = \ lambda \ cdot x_ {n} \ cdot (1-x_ {n} ^ {2})$

Kesimpulan:

Masalah pendidikan dipecahkan dalam artikel: apakah entropi informasi merupakan ukuran kekacauan, dan jawaban atas pertanyaan ini secara afirmatif diberikan oleh Python.

Entropi Informasi Kekacauan

Pendahuluan

Mekanisme transisi dari tatanan ke kekacauan

Entropi informasi dan koefisien entropi

Entropi informasi sebagai ukuran kekacauan

Kesimpulan:

Referensi

More articles: