Pada estimasi autoregresif kepadatan spektral dari sinyal stasioner

Metode estimasi spektral proses acak stasioner berdasarkan fast Fourier transform (FFT) telah dikenal luas dan banyak digunakan dalam praktik rekayasa. Kerugiannya termasuk, khususnya, dispersi tinggi (akurasi rendah) dari estimasi dengan interval pengamatan yang tidak cukup panjang untuk proses, yang biasanya secara visual memanifestasikan dirinya dalam grafik "indentasi" yang kuat dari kepadatan spektral daya (PSD). Salah satu metode alternatif estimasi spektral adalah metode autoregresif, dipertimbangkan dalam contoh di bawah ini, yang jauh kurang dikenal dalam praktik teknik. Dalam banyak kasus, metode ini membuatnya relatif mudah untuk memperoleh perkiraan PSD yang jauh lebih baik (Gambar 1), dan kadang-kadang bahkan informasi yang lebih dalam tentang proses acak yang sedang diteliti.


Gambar. 1 Evaluasi klasik dan autoregresif dari proses "pendek" PSD

Untuk tujuan demonstrasi, sinyal waktu diskrit (urutan) x [i] disintesis. Sinyal dimodelkan menggunakan model ARMA (filter digital) yang mensimulasikan sifat-sifat sistem mekanis (1) - memindahkan titik material x (t) dalam osilator "massa tunggal" dengan parameter m = 1 kg, c = 100 N / m, k = 2, 5 kg / s, dan dengan gangguan gaya - Gaussian "putih" (memperhitungkan diskritisasi) kebisingan f (t) dengan dispersi 1 N ² , interval pengambilan sampel dalam waktu Δt = 0,12 s.



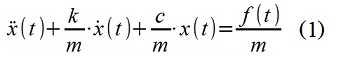
Model dibangun (2). Metode membangun model sudah dipertimbangkan sebelumnya di sini .

x [i] - 0,6388 · x [i-1] + 0,7408 · x [i-2] = 0,009667 · f [i-1] (2)

Dengan menggunakan (2), urutan 50 ribu sampel disintesis, di mana generator dari variabel acak terdistribusi normal () dari lingkungan perangkat lunak yang terkenal digunakan.

Setelah simulasi proses x [i] selesai, parameter kuantitatif model (2) diasumsikan tidak diketahui - hanya proses itu sendiri dan, sampai batas tertentu, informasi tentang sifat-sifat model dalam istilah yang paling umum tersedia untuk penelitian.

Estimasi spektral dari urutan 50.000 poin dilakukan menggunakan metode Welch, ukuran segmen diambil sama dengan 256 sampel, jendela Hamming dan 60% tumpang tindih segmen diterapkan. Standar deviasi dari estimasi tersebut, berdasarkan pada fakta bahwa urutan memiliki panjang sekitar 200 segmen yang tidak tumpang tindih, dapat diperkirakan secara kasar sekitar ~ 7%.

Lebih lanjut, dengan asumsi bahwa dalam kondisi nyata dalam percobaan, urutan yang jauh lebih pendek tersedia untuk penelitian, studi dilakukan hanya pada 500 sampel pertama dari sinyal ini.

Estimasi diperoleh dengan metode Welch dengan parameter yang sama. Deviasi standar dari estimasi tersebut adalah ~ 70%, "kekasaran" grafik yang sangat kuat terlihat (Gbr. 2).


Gambar 2. Evaluasi PSD dari proses "panjang" dan "pendek" dengan metode klasik

Berdasarkan pada fakta bahwa kita mengetahui bentuk perkiraan fungsi (grafik) dari proses SPM (misalnya, berdasarkan sifat fisik yang diketahui dari proses - osilator massa tunggal di bawah white noise, atau dari mengevaluasi proses serupa yang membutuhkan implementasi lebih lama), kami memutuskan untuk mengevaluasi dengan menggunakan model autoregresif orde dua (AR (2), atau = ARMA (2.0)).

Menentukan urutan model adalah hal yang sangat penting, kesalahan dalam urutan dapat menyebabkan kesalahan yang sangat besar dalam hasil estimasi. Ada metode yang belum dipertimbangkan di sini, membantu menentukan urutan model berdasarkan hanya proses yang dianalisis.

Estimasi parameter model dilakukan dengan menggunakan persamaan Yule-Walker yang terkenal untuk proses autoregresif (sedikit dimodifikasi untuk sedikit menyederhanakan struktur skrip):



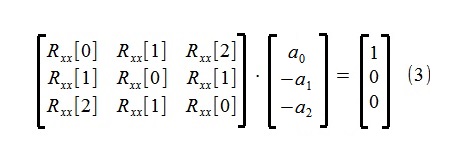
Seperti dapat dilihat dari persamaan, untuk menentukan parameter, hanya tiga anggota pertama dari urutan autoregresif Rxx [0], Rxx [1], Rxx [2], yang diperkirakan dari urutan 500-titik awal x [i] dengan metode korelogram, digunakan ~ 4,5%.

(Omong-omong, jelas bahwa "kontra" sebelum ₁ , a _{2 2} , dll., Sangat tidak nyaman. Mereka muncul karena penggunaan model ARMA yang dominan "prediktif" dalam perekonomian, dalam sumber "rekayasa" mereka sebelumnya. Tidak. Saya sudah ragu bahwa perlu menggunakan pemahaman tentang koefisien AR di sini.)

Matriks korelasi dalam (3) dalam praktik selalu memiliki prevalensi diagonal yang ketat | Rxx [0] | > | Rxx [i] |, termasuk karena kehadiran suara-suara pengamatan, yang karenanya tidak ada kesulitan dengan penanganannya (menemukan solusi (3)).

(Untuk memperjelas pertanyaan besarnya kesalahan pemodelan statistik, menarik untuk menyebutkan, misalnya, perkiraan Rxx [0] = 2.2606e-04 m ^{2 yang} diperoleh dari 500 sampel, dibandingkan dengan korelogram yang diperoleh perkiraan dispersi dari 50.000 sampel, = 2.4238e-04 m ² dan estimasi dengan integrand area PSD yang diperoleh dengan metode Welch untuk 50.000 sampel (Gbr. 2), = 2.4232e-04 m ² )

Setelah mengganti estimasi yang ditemukan Rxx [i], kami memiliki:



Parameter model berikut ditentukan a ₀ = 11325.9; a ₁ = 7090.1; a ₂ = -8411.5; Seperti yang dapat dilihat dari (3), dispersi dari white noise masuk hipotetis ditetapkan = 1 di sini, menentukan bukannya mendapatkan gain ₀ . Estimasi autoregresif dari PSD dibangun oleh transformasi Fourier atas urutan koefisien a ₀ , a ₁ , a ₂ :




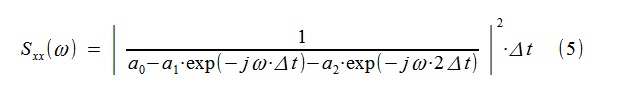
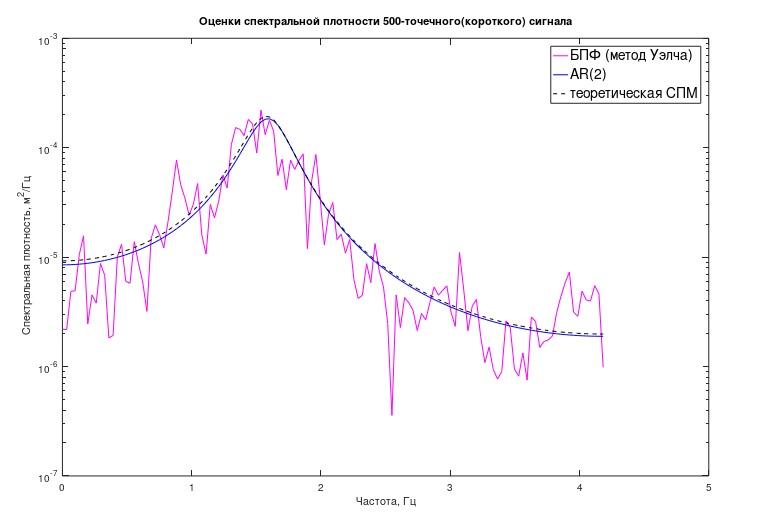Gambar. 3 Evaluasi klasik dan autoregresif dari proses "pendek" PSD

Dengan cara yang sama, menurut ungkapan yang mirip dengan (5), jadwal "teoritis" dari PSD sebelumnya dibuat, hanya koefisien model di sana, tentu saja, diambil berbeda (dari (2)).
Dapat dilihat dari grafik bahwa estimasi AR dari PSD ternyata sangat dekat dengan yang diharapkan secara teoritis. Selain grafik, dimungkinkan untuk mencoba mengevaluasi beberapa karakteristik analitis dari proses dan sistem mekanik yang terkait. Dalam hal ini, ini adalah "kutub" model, secara numerik mengkarakterisasi frekuensi dari "resonansi" puncak model dan "faktor kualitas" yang terkait.

Dari (5) kami menemukan hubungan untuk mencari diskontinuitas fungsi transfer model kami menggunakan Transformasi Laplace (menggantikan jω dengan λ = -ε + jω):



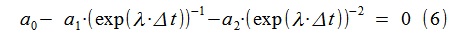
Untuk model AR yang diperoleh, λ _1,2 = -1,5427 ± j · 10,1514 dihitung dengan cara ini, yang sangat dekat dengan model asli yang digunakan untuk menghasilkan proses
λ _{1.2 theor} = -1.2500 ± j · 9.9216 (yaitu, posisi puncak resonansi, masing-masing, 1.615 Hz (dalam teori) dan 1.579 Hz (ditentukan)).


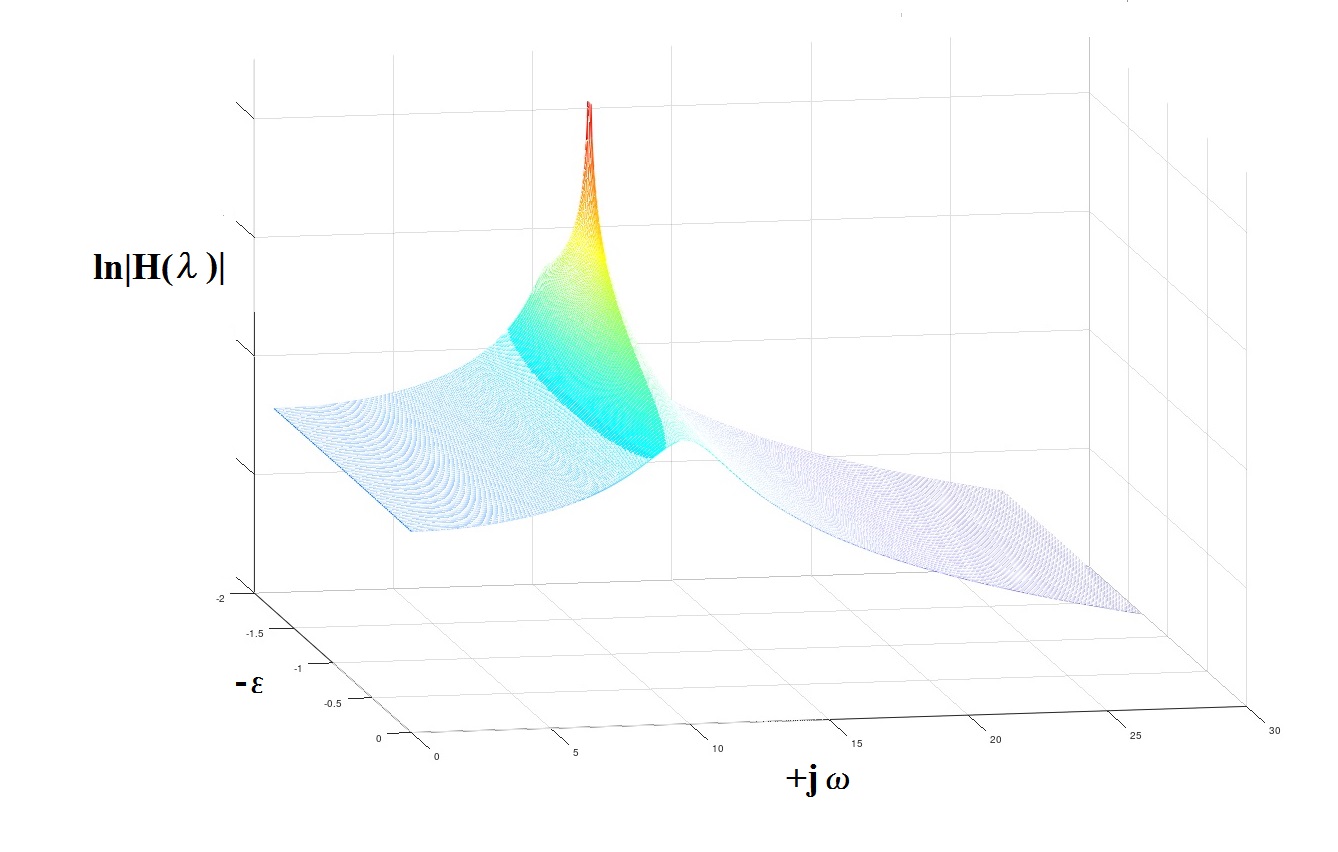Gbr. 4 Tentang konsep "kutub"

Beberapa komentar dan rekomendasi sebagai kesimpulan.

1. Urutan "berlebihan" (terlalu besar) dari model AR biasanya jauh lebih tidak berbahaya daripada tidak cukup, dari sudut pandang risiko memperoleh estimasi PSD dengan kesalahan kotor.
2. Sebagai aturan, pemodelan AR memungkinkan untuk cukup akurat menentukan frekuensi resonansi jωk dan jauh lebih akurat menentukan lebar "puncak" yang sesuai -ε _k
3. ARMA - model dapat berubah menjadi urutan yang jauh lebih kecil (ukuran) daripada model AR, yang tampaknya ditujukan untuk meningkatkan akurasi model, menurut banyak sumber. Namun, mengevaluasi bagian-MA dari model jauh lebih sulit dan umumnya dapat mencakup langkah pertama dalam mendapatkan model-AR besar-besaran untuk selanjutnya mengubahnya menjadi bagian-MA. Sehubungan dengan sumber-sumber ini, pendapat alternatif juga diungkapkan tentang kelayakan menggunakan model-AR yang tepat untuk estimasi spektral, meskipun dari orde yang lebih tinggi.
4. Untuk proses yang sangat singkat, juga non-stasioner, alih-alih matriks estimasi fungsi autokorelasi, matriks kovarians biasanya digunakan dalam (3).
5. Untuk studi rinci tentang masalah estimasi spektral autoregresif, S.L. Marple ml. "Analisis spektral digital dan aplikasinya", M., Mir, 1990