Dalam komunitas ilmiah, visualisasi data dan desain teori memainkan peran yang sangat penting. Alat yang mengimplementasikan perintah LaTeX , seperti Markdown dan MathJax, sering digunakan untuk presentasi formula yang nyaman dan indah.

Untuk Julia, ada juga satu set paket yang memungkinkan Anda menggunakan sintaksis LaTeX , dan dalam hubungannya dengan sarana aljabar simbolis, kami mendapatkan alat yang kuat untuk menangani formula.

Unduh dan sambungkan semua yang Anda butuhkan untuk hari ini

using Pkg Pkg.add("Latexify") Pkg.add("LaTeXStrings") Pkg.add("SymEngine") using Latexify, LaTeXStrings, Plots, SymEngine

LaTeXStrings

LaTeXStrings adalah paket kecil yang membuatnya mudah untuk memasukkan persamaan LaTeX dalam literal string Julia. Saat menggunakan string biasa di Julia untuk memasukkan string literal dengan persamaan LaTeX yang disematkan, Anda harus secara manual menghindari semua garis miring terbalik dan tanda dolar: misalnya, $ \alpha^2 $ ditulis \$\\alpha^2\$ . Selain itu, meskipun IJulia mampu menampilkan persamaan berformat LaTeX (via MathJax ), ini tidak akan bekerja dengan garis biasa. Oleh karena itu, paket LaTeXStrings mendefinisikan:

Kelas LaTeXString (subtipe String ) yang berfungsi seperti string (untuk pengindeksan, konversi, dll.), Tetapi secara otomatis ditampilkan sebagai teks / lateks di IJulia.
Makro string L"..." dan L"""...""" yang memungkinkan Anda untuk memasukkan persamaan LaTeX tanpa melarikan diri dari garis miring terbalik dan tanda dolar (dan yang menambahkan tanda dolar untuk Anda jika Anda menghilangkannya).

 S = L"1 + \alpha^2"

REPL akan menampilkan :

 "\$1 + \\alpha^2\$"

dan Jupyter akan menampilkan:

1 + a l p h a^{2}

$1 + \ alpha ^ 2$

Pengindeksan berfungsi seperti garis normal:

 S[4:7] "+ \\a"

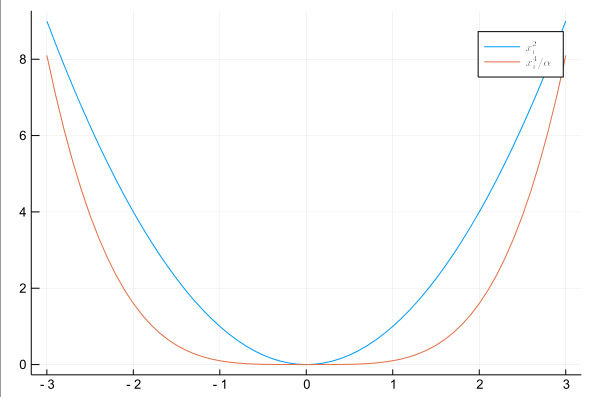
Garis-garis seperti itu dapat bermanfaat dalam desain grafik.

 x = [-3:0.1:3...] y1 = x .^2 α = 10 y2 = x .^4 / α; plot(x,y1, lab = "\$x^2_i\$") plot!(x,y2, lab = L"x^4_i/\alpha")

Latekskan

Paket yang lebih fungsional adalah Latexify ( Guide ). Ini dirancang untuk menghasilkan matematika LaTeX dari objek julia. Paket ini menggunakan homologi Julia untuk mengonversi ekspresi menjadi string dalam format LaTeX. Latexify.jl menyediakan fungsi untuk mengonversi sejumlah objek Julia yang berbeda, termasuk:

Ekspresi
String
Bilangan (termasuk rasional dan kompleks),
Ekspresi simbolik dari SymEngine.jl,
ParameterizedFunctions and ReactionNetworks dari DifferentialEquations.jl
serta array dari semua jenis yang didukung.

 ex = :(x/(y+x)^2) #  latexify(ex)

f r a c x k i r i (y + x k a n a n)^{2}

$\ frac {x} {\ kiri (y + x \ kanan) ^ {2}}$

 str = "x/(2*k_1+x^2)" #  latexify(str)

f r a c x 2 c d o t k_{1} + x^{2}

$\ frac {x} {2 \ cdot k_ {1} + x ^ {2}}$

Array elemen heterogen:

 m = [2//3 "e^(-c*t)" 1+3im; :(x/(x+k_1)) "gamma(n)" :(log10(x))] latexify(m)

\ left [\ begin {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} & 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} & \ Gamma \ kiri (n \ kanan) & \ log_ {10} \ kiri (x \ kanan) \\ \ end {array} \ kanan]

$\ left [\ begin {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} & 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} & \ Gamma \ kiri (n \ kanan) & \ log_ {10} \ kiri (x \ kanan) \\ \ end {array} \ kanan]$

Anda bisa menentukan fungsi yang menampilkan rumus dan menyalinnya ke buffer dalam bentuk yang bisa dimengerti oleh Habr:

 function habr(formula) l = latexify(formula) res = "\$\$display\$$l\$display\$\$\n" clipboard(res) return l end habr(ex)

f r a c x k i r i (y + x k a n a n)^{2}

$\ frac {x} {\ kiri (y + x \ kanan) ^ {2}}$

 <p>$<!-- math>$$display$$\frac{x}{\left( y + x \right)^{2}}$$display$$</math -->$</p>

Ingatlah selalu

 latexify("x/y") |> display

f r a c x y

$\ frac {x} {y}$

 latexify("x/y") |> print

$\frac{x}{y}$

Symengine

SymEngine adalah paket yang menyediakan perhitungan simbolik yang dapat Anda visualisasikan di Jupyter Anda dengan Latexify.
Anda dapat menentukan karakter dalam garis dan kutipan ( quote ):

 julia> a=symbols(:a); b=symbols(:b) b julia> a,b = symbols("ab") (a, b) julia> @vars ab (a, b)

Tentukan matriks dan tampilkan dengan indah

 u = [symbols("u_$i$j") for i in 1:3, j in 1:3] 3×3 Array{Basic,2}: u_11 u_12 u_13 u_21 u_22 u_23 u_31 u_32 u_33 u |> habr

\ left [\ begin {array} {ccc} u_ {11} & u_ {12} & u_ {13} \\ u_ {21} & u_ {22} & u_ {23} \\ u_ {31} & u_ {32} & u_ {33} \\ \ end {array} \ kanan]

$\ left [\ begin {array} {ccc} u_ {11} & u_ {12} & u_ {13} \\ u_ {21} & u_ {22} & u_ {23} \\ u_ {31} & u_ {32} & u_ {33} \\ \ end {array} \ kanan]$

Misalkan kita memiliki vektor

 C = symbols("Ω_b/Ω_l") J = [symbols("J_$i") for i in ['x','y','z'] ] h = [0, 0, symbols("h_z")] 3-element Array{Basic,1}: 0 0 h_z

yang harus dikalikan vektor

 using LinearAlgebra × = cross latexify(J×h, transpose = true)

$$ menampilkan $$ \ mulai {persamaan} \ kiri [\ mulai {array} {c} J_ {y} \ cdot h_ {z} \\ - J_ {x} \ cdot h_ {z} \\ 0 \\ \ end {array} \ kanan] \ end {persamaan} $$ menampilkan $$Perhitungan matriks penuh:

 dJ = C*(u*J.^3)×h latexify( dJ, transpose = true) habr(ans)

$$ menampilkan $$ \ mulai {persamaan} \ kiri [\ mulai {array} {c} \ frac {h_ {z} \ cdot \ kiri (u_ {21} \ cdot J_ {x} ^ {3} + u_ { 22} \ cdot J_ {y} ^ {3} + u_ {23} \ cdot J_ {z} ^ {3} \ kanan) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ \ frac { - h_ {z} \ cdot \ kiri (u_ {11} \ cdot J_ {x} ^ {3} + u_ {12} \ cdot J_ {y} ^ {3} + u_ {13} \ cdot J_ {z} ^ {3} \ kanan) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ 0 \\ \ end {array} \ kanan] \ end {persamaan} $$ menampilkan $$tetapi dengan rantai sederhana seperti itu Anda dapat menemukan penentu dan mengirimkannya ke Habr

 u |> det |> habr

u_{11} c d o t k i r i (u_{22} - f r a c u_{12} c d o t u_{21} u_{11} k a n a n) c d o t k i r i (u_{33} - f r a c u_{13} c d o t u_{31} u_{11} - f r a c l e f t (u_{23} - f r a c u_{13} c d o t u_{21} u_{11} k a n a n) c d o t k i r i (u_{32} - f r a c u_{12} c d o t u_{31} u_{11} k a n a n) u_{22} - f r a c u_{12} c d o t u_{21} u_{11} k a n a n)

$u_ {11} \ cdot \ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ kanan)$

Rekursif! Matriks terbalik mungkin dihitung dengan cara yang sama:

 u^-1 |> habr

Spoiler

$$ menampilkan $$ \ kiri [\ mulai {array} {ccc} \ frac {1 - \ frac {u_ {12} \ cdot \ kiri (\ frac {- u_ {21}} {u_ {11}} - \ frac {\ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31 }} {u_ {11}} \ kanan)} {u_ {11} \ cdot \ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan) } \ kanan) \ cdot \ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan)} {u_ {33} - \ frac {u_ {13 } \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ { 21}} {u_ {11}}} kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} - \ frac {u_ {13} \ cdot \ kiri (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31 }} {u_ {11}} \ kanan)} {u_ {11} \ cdot \ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan) } \ kanan)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u _ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}}} {u_ {11}} & \ frac {\ frac {- u_ {12} \ cdot \ left (1 + \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {\ kiri (u_ {22 22 } - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} { u_ {11}} - \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} } \ kanan)} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} + \ frac {u_ {13} \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {\ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21} } {u_ {11}} \ kanan) \ cdot \ kiri (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ kiri (u_ {23 23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} { u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ rig ht)}} {u_ {11}} & \ frac {\ frac {- u_ {13}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12 } \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} + \ frac { u_ {12} \ cdot \ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan)} {\ kiri (u_ {22} - \ frac { u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ { 12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ kanan)} } {u_ {11}} \\ \ frac {\ frac {- u_ {21}} {u_ {11}} - \ frac {\ kiri (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {11} \ cdot \ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan)} \ kanan) \ cdot \ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ { 12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {1 + \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} { \ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ kanan)}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {- \ kiri (u_ {23 23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan)} {\ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} { u_ {11}} \ kanan) \ cdot \ kiri (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ kiri (u_ {23} - - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac { u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ benar )} \\ \ frac {\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {11} \ cdot \ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan)}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} { u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} & \ frac {- \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {\ kiri (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21 }} {u_ {11}} \ kanan) \ cdot \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ kanan)} & \ kiri (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} { u_ {11}} - \ frac {\ kiri (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ kanan) \ c titik \ kiri (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ kanan)} {u_ {22} - \ frac {u_ {12} \ cdot u_ { 21}} {u_ {11}}} \ kanan) ^ {- 1} \\ \ end {array} \ kanan] $$ tampilkan $$

Jika Anda ingin melukai Matjax peramban Anda, tulis minus derajat kedua (kuadrat dari matriks terbalik)Omong-omong, SymEngine mempertimbangkan turunan:

 dJ[1] |> habr

f r a c h_{z} c d o t k i r i (u_{21} c d o t J_{x}^{3} + u_{22} c d o t J_{y}^{3} + u_{23} c d o t J_{z}^{3} k a n a n) c d o t O m e g a_{b} O m e g a_{l}

$\ frac {h_ {z} \ cdot \ kiri (u_ {21} \ cdot J_ {x} ^ {3} + u_ {22} \ cdot J_ {y} ^ {3} + u_ {23} \ cdot J_ {z} ^ {3} \ kanan) \ cdot \ Omega_ {b}} {\ Omega_ {l}}$

 diff(dJ[1], J[1]) |> habr

f r a c 3 c d o t J_{x}^{2} c d o t h_{z} c d o t u_{21} c d o t O m e g a_{b} O m e g a_{l}

$\ frac {3 \ cdot J_ {x} ^ {2} \ cdot h_ {z} \ cdot u_ {21} \ cdot \ Omega_ {b}} {\ Omega_ {l}}$

Ngomong-ngomong, Julia tidak hanya bisa menggunakan rumus, tetapi juga grafik dari LaTeX 'a. Dan jika Anda menginstal MikTex dan sudah mengunduh pgfplot , maka dengan menggunakan lingkungan yang sesuai Anda dapat berteman dengan Julia, yang akan memberikan kesempatan untuk membangun histogram, grafik tiga dimensi, kesalahan dan relief dengan kontur, dan kemudian mengintegrasikannya ke dalam dokumen LaTeX.

Itu semua dengan formula, tetapi tidak dengan perhitungan simbolis: Julia masih memiliki solusi yang lebih kompleks dan menarik untuk aljabar simbolis, yang pasti akan kita hadapi di waktu mendatang.

Julia dalam lateks

Unduh dan sambungkan semua yang Anda butuhkan untuk hari ini

LaTeXStrings

Latekskan

Symengine

More articles: