Tentang kedekatan puncak

“Sebelum kamu memahami ini, sepertinya seperti keajaiban. Tetapi setelah itu tidak ada yang istimewa. ”

Tidak, bukan tentang gunung, - tentang jumlah. Dalam matematika, ada pertanyaan yang rumusannya dapat diakses oleh semua orang, tetapi solusinya tidak trivial dan tanpa persiapan khusus sulit untuk dijelaskan. Salah satu masalah ini dapat dinyatakan secara singkat sebagai berikut: bagaimana cara menghitung jarak dalam grafik yang diarahkan dengan benar? Masalah yang agak abstrak ini dapat direduksi menjadi tugas memotivasi yang sangat spesifik. Cocok dalam satu gambar:

1. Pernyataan masalah. Saya hidup di satu, tetapi Anda di yang lain.

Sebuah kota kecil dibagi (misalnya, oleh sungai, meskipun dalam konteks puncak ngarai lebih cocok) menjadi dua kabupaten (bagian) $$$A$ dan $$$B$ . Komunikasi antar kabupaten dilakukan di sepanjang satu jalan (jembatan), yang memiliki dua lajur: ke samping $$$A$ untuk $$$B$ dan sebaliknya. Sehubungan dengan pertumbuhan populasi, muncul pertanyaan tentang peningkatan kapasitas jalan. Uang seperti biasa hampir tidak cukup dan hanya cukup untuk satu jalur dalam satu arah. Jelas bahwa bahkan satu jalur akan menyatukan daerah, tetapi pertanyaannya adalah seberapa tepatnya? Anda adalah ahli matematika gila urban, dan Andalah yang diundang untuk menerima jawaban yang masuk akal .

Seberapa dekat area jika Anda membangun jalur lain di satu arah?

Kata-kata untuk tingkat lanjut

Alih-alih jembatan Konigsberg , bahasa teori grafik yang sedikit lebih keras dapat digunakan. Jadi, ada grafik terarah dengan dua simpul (node) $$$A$ dan $$$B$ . Besarnya koneksi (konduktivitas, bandwidth) pada arah maju dan mundur pada awalnya sama. Pertanyaannya adalah berapa banyak jarak antar node akan berubah jika konduktivitas di salah satu arah digandakan?

Dan ya, jika Anda seorang ahli matematika yang hebat, Anda dapat menawarkan (dan membenarkan) solusi untuk nilai langsung dan umpan balik apa pun. Idealnya, untuk grafik dengan sejumlah node dan tautan.

Keintiman dan pengembaraan mabuk

Jelas bahwa jarak (kilometer) biasa antar daerah tidak tergantung pada ada atau tidak adanya jalan. Karena itu, tidak cocok di sini - kita perlu mengandalkan komunikasi. Semakin banyak kabupaten yang terhubung - semakin dekat mereka - semakin banyak penduduk dapat mencapai daerah lain per unit waktu.

Untuk menilai ukuran kedekatan antara node dari grafik yang tidak diarahkan, yang disebut jarak resistif dapat digunakan. Sebelumnya, kami sudah menggambarkan properti dari jarak ini di habr di beberapa artikel .

Jarak resistif setara dengan konsep resistensi efektif, ketika datang ke jaringan listrik. Oleh karena itu, dalam bahasa elektrik, masalahnya dapat dirumuskan sebagai berikut. Antara dua node, dua dioda dengan konduktivitas yang sama saling berlawanan. Bagaimana resistensi antara titik-titik ini akan berubah jika Anda menambahkan dioda lain? (Saya minta maaf jika bahasa listrik gagal dan saya menulis omong kosong di sini).

Juga, resistensi yang efektif dapat ditafsirkan dalam bahasa Markov untuk kemungkinan berjalan acak mabuk (bagi mereka yang ingin mempelajari topik - google "Jalan acak dan jaringan listrik").

Jarak resistif adalah kuadrat, - sesuai dengan kuadrat dari jarak linear. Jarak kuadratik juga disebut quadrans . Tetapi karena jarak (linear) lainnya tidak digunakan dalam masalah ini, kita tidak perlu istilah quadrans di sini. (Ada cukup lidah burung bahkan tanpa itu).

Secara umum, istilah "jarak resistif" juga tidak terlihat bagus. Dia menyiratkan bahwa kita berbicara tentang semacam jarak yang tidak biasa dengan ilmu pengetahuan. Bahkan, jarak resistif adalah jarak Euclidean biasa. Tetapi di ruang affine. Kami menggunakan fitur ini lebih lanjut.

Dan apa sebenarnya masalahnya?

Jika kita tahu apa "jarak resistif" itu, mengapa kita tidak bisa "mengambil dan menghitungnya" untuk grafik tertentu?

Hm Pada prinsipnya mudah. Jika kita berbicara tentang grafik yang tidak diarahkan. Jika kota telah membangun strip di kedua arah, maka jarak resistif akan berkurang tepat setengahnya. Karena perlawanan berbanding terbalik dengan konduktivitas, dan konduktivitas (throughput) telah berlipat ganda. Dan jika saya menambahkan dua band di setiap arah, maka jaraknya akan berkurang 3 kali. Semuanya cukup sepele di sini. (Dan mungkin, seseorang di sini sudah bisa menebak bentuk umum dari solusi. Dan kita melangkah lebih jauh).

Ketika hubungan lawan tidak sama, maka semuanya menjadi rumit. Dan sangat parah.

Tidak ada cara hukum sederhana yang diterima secara umum untuk menentukan kedekatan puncak (jarak resistif) dalam grafik arah .

(Ini tesis saya - mungkin seseorang dapat meyakinkan saya). "Tidak" - di sini berarti tidak ada di buku teks, wiki, dan di kepala (lebih tepatnya - ada banyak cara berbeda dari penulis yang berbeda yang memerlukan asumsi dan definisi yang berbeda). Ada caranya (meski tidak begitu sederhana). Pada artikel ini, kami hanya menggambarkannya.

Penentuan jarak dengan adanya koneksi terarah memerlukan klarifikasi jika kita berbicara tentang grafik berarah (metrik non-komutatif, saya minta maaf). Anda dapat berbicara tentang jarak dari $$$A$ sebelumnya $$$B$ , tetapi Anda dapat dari $$$B$ sebelumnya $$$A$ . Dan kemungkinan besar jarak ini tidak selalu sama. Jarak seperti apa yang kita bicarakan dalam masalah?

Aturan jarak Euclidean

Kami akan muncul dan mengambil napas dalam-dalam. Kami telah menyebutkan bahwa jarak resistif adalah Euclidean biasa. Ini berarti bahwa definisinya dapat direduksi menjadi definisi jarak Euclidean sebagai norma perbedaan dua elemen:

$$$S (A, B) = | A - B | ^ 2 = (A - B) ^ 2 = (A - B) \ cdot (A - B) = S (B, A) \ quad (1)$

Definisi ini tidak tergantung pada urutan elemen - ini adalah jarak komutatif, kedekatan (lebih tepatnya, jarak) elemen. Titik dalam ekspresi berarti operasi produk skalar (ruang metrik). Dengan demikian, ungkapan (1) dapat diungkapkan:

$$$S (A, B) = S (B, A) = A ^ 2 + B ^ 2 - A \ cdot B - B \ cdot A \ quad (2)$

Di sini $$$A ^ 2 = A \ cdot A$ , $$$B ^ 2 = B \ cdot B$ - norma-norma elemen. Ketika datang ke grafik, maka norma-norma elemen biasanya nol. Dalam masalah aslinya tidak ada yang dikatakan tentang norma-norma, sehingga Anda dapat menjadikannya nol (lebih lanjut tentang apa arti unsur-unsur elemen dalam ruang affine. Di sini , dan bahkan lebih detail, di sini ). Kemudian ekspresi untuk jarak yang diinginkan mengambil bentuk:

$$$S (A, B) = - (A \ cdot B + B \ cdot A) = s_ {AB} + s_ {BA} \ quad (3)$

Menurut ungkapan (3), semua yang diperlukan untuk menyelesaikan masalah adalah menemukan produk skalar elemen (node) dalam grafik terarah (mudah dikatakan, tetapi bagaimana melakukan ini?).

Sepanjang jalan, rumus (3) menunjukkan bahwa kita umum (komutatif) mengukur kedekatan antara elemen $$$A$ dan $$$B$ adalah jumlah dari dua jarak terarah:

$$$s_ {AB} = - A \ cdot B$ - jarak terarah dari $$$A$ sebelumnya $$$B$ ,
$$$s_ {BA} = - B \ cdot A$ - jarak terarah dari $$$B$ sebelumnya $$$A$ .

2. Keputusan. Jalan panjang di bukit pasir

Gemuruh mereda. Kesenangan sudah berakhir. Kemudian datang detail yang membosankan dari deskripsi esensi dari metode untuk menghitung produk skalar antara node dari grafik yang diarahkan. Ini adalah bagian yang saya tidak tahu bagaimana mengatakan "dengan cara sederhana di jari". Namun disinilah hal terpenting dalam artikel. Sesuatu yang berharga membuang-buang waktu untuk itu.

Garis penalaran umum adalah sebagai berikut. Kami dengan hati-hati dan tanpa emosi asumsi tambahan baru mentransfer sifat metrik ruang simetris yang diketahui ke yang asimetris. Yang diperlukan hanyalah memperhitungkan kekhasan metrik di ruang affine.

Setiap grafik yang terhubung (diarahkan atau tidak) menentukan ruang metrik affine. Beberapa properti dari ruang tersebut dalam eksekusi simetris (komutatif) dijelaskan secara serampangan dalam seri artikel yang telah disebutkan atau lebih tepatnya dan lebih rinci dalam longrid yang disebutkan. Jangan terburu-buru untuk beralih - di bawah ini kami memberikan (meskipun, oleh twister lidah) meremas utama.

Affine metric space (grafik tidak berarah)

Yang penting Terkenal dulu.

1. Afinitas ruang berarti konsep vektor dan elemen dalam ruang berbeda. Vektor adalah perbedaan elemen. Fitur yang tampaknya tidak signifikan ini menimbulkan konsekuensi yang signifikan jika metrik didefinisikan dalam ruang.

2. Ruang didefinisikan oleh basis yang terdiri dari elemen. Verteks grafik adalah dasar ruang. Hubungan dalam grafik menentukan properti metriknya.

3. Karakteristik konektivitas grafik adalah matriks kedekatan . Tetapi untuk properti metrik (dan lainnya), Laplacian dari grafik (matriks Kirchhoff) lebih penting $$$L$ .

4. Laplacian grafik adalah tensor yang hampir metrik. "Hampir" - di sini berarti itu tidak lengkap. Laplacian adalah matriks degenerasi dan karenanya tidak dapat dibalik. Dan tensor metrik standar sepenuhnya dapat dibalik.

Sekarang kurang dikenal.

5. Perbedaan antara elemen dan vektor dalam ruang affine metrik mengarah ke keberadaan vektor nol di dalamnya $$$\ mathbb z$ . Produk skalar elemen dengan vektor nol dalam ruang komutatif (simetris) sama dengan kesatuan (dalam ruang non-komutatif itu tergantung pada arah multiplikasi). Tanpa vektor nol, ruang grafik tidak lengkap! Ini penting.

6. Pusat ortogonal dasar adalah ganda sehubungan dengan vektor nol. $$$Z$ . Ini adalah elemen yang ortogonal untuk semua elemen lain dari basis (kecuali untuk vektor-nol). Ingatlah bahwa ortogonalitas unsur berarti produk skalarnya nol. Orthocenter segitiga adalah lingkaran yang dibatasi . Ya, dalam ruang affine penuh elemen dengan norma bukan nol bukanlah sebuah titik, tetapi sebuah bola dimensi-n.

7. Laplacian grafik, bersama dengan koordinat pusat ortogonal, menjadi lengkap (tensor metrik penuh). Dengan kata lain, Laplacian penuh $$$Lm$ Merupakan hitungan biasa laplacian $$$L$ tetapi dibatasi oleh koordinat barikentrik pusat ortogonal.

8. Inversi Laplacian penuh memungkinkan seseorang untuk mendapatkan Gramian lengkap $$$Gm$ - matriks produk skalar dari elemen-elemen dasar (dalam kasus kami, simpul grafik). Gramian ini juga merupakan tensor metrik ruang penuh.

9. Pembingkaian gramian penuh adalah tupel unit (produk skalar elemen dasar dan vektor-nol). Di sudut - nol, ini adalah norma dari vektor-nol itu sendiri.
Matriks Cayley-Menger yang terkenal adalah Gramian yang hampir teratur.

Sebagai hasilnya, kami menyimpulkan bahwa, menurut klaim 8, masalah penentuan produk skalar (dan, karenanya, jarak) antara node grafik berkurang untuk menentukan tensor metrik awal dari basis $$$Gm$ .

Kami membutuhkan metode untuk membuat grafik gram penuh $$$Gm$ untuk Laplacian tertentu (tidak lengkap) $$$L$ .

Dalam kasus ikatan simetris, pembangunan Gramian lengkap dari Laplacian (dan sebaliknya) tidak menyebabkan kesulitan khusus. Dalam hal ini, produk skalar dari elemen-elemen dasar dan vektor-nol bersifat komutatif - mereka tidak bergantung pada urutan perkalian:

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

Untuk grafik berarah (ruang non-komutatif) masalahnya rumit. Kalau saja karena jumlah koneksi yang sangat mungkin dalam grafik diarahkan dua kali lipat.

Ruang affine non-komutatif (grafik berarah)

Tentang properti Laplacian dari grafik yang diarahkan, kami juga sudah menulis di Habr . Mereka memberi tahu cara menggunakan potensi Laplacian untuk memeringkat objek. Dalam hal basis, potensi Laplacian adalah koordinat ganda dari vektor-nol (annihilator dari Laplacian).

Pada artikel ini, kami tertarik pada properti metrik. Jika grafik diarahkan, maka produk skalar antara simpulnya tergantung pada urutan:

$$$A \ cdot B \ ne B \ cdot A$

Ini berarti bahwa koordinat ganda dalam grafik diarahkan dibagi (ke kiri dan kanan). Nilai-nilai produk skalar dari vektor-nol dan elemen-elemen dasar (berbatasan dengan gramian) juga tergantung pada urutan faktor-faktornya. Dan oleh karena itu, berbeda dengan ruang komutatif, di sini setengah dari koordinat ganda vektor-nol tidak diketahui dan harus ditentukan.

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb $$

Namun, ada banyak jumlah yang diketahui.

Pertama, Laplacian sendiri dikenal. Selain itu, diketahui bahwa jumlah barisnya adalah nol (dalam kasus umum, ini merupakan persyaratan opsional, tetapi untuk Laplacians dari grafik yang diarahkan biasanya demikian halnya). Penting juga bahwa koordinat barikentrik elemen unik, karena mereka independen terhadap metrik ruang. Artinya, batas Laplacian grafik simetris untuk grafik yang diarahkan dan yang tidak terarah (saya tidak segera mengenali titik ini). Akhirnya, kita mengetahui norma-norma unsur-unsur dasar (biasanya dalam grafik mereka sama dengan nol).

Tetap mengganti semua yang diketahui dan tidak dikenal dalam identitas yang menghubungkan orang Laplacian dan Gramian:

$$$Lm \ Gm = I$

Di sini $$$I$ Merupakan matriks identitas. Dalam identitas ini, makna transisi dari Laplacian yang tidak lengkap ke yang lengkap.

Diam dan percaya

Mari kita beralih dari kata-kata ke perbuatan. Beginilah tampilan Laplacian $$$L$ untuk grafik dua node:

$$$L = \ begin {bmatrix} c_1 & -c_1 \\ c_2 & -c_2 \ end {bmatrix}$

Untuk mempermudah, kami telah menetapkan hubungan dengan angka: $$$c_1 = c_ {AB}, c_2 = c_ {BA}$ . Diasumsikan bahwa nilai-nilai obligasi diketahui - melalui mereka kami akan mengungkapkan semua jumlah lainnya.

Laplacian penuh $$$Lm$ termasuk koordinat orthocenter $$$[rz, az, bz]$ :

$$$Lm = \ begin {bmatrix} rz & az & bz \\ az & c_1 & -c_1 \\ bz & c_2 & -c_2 \ end {bmatrix}$

Di sini $$$rz$ - norma orthocenter (dalam kasus simetris ditafsirkan sebagai kuadrat jari-jari), $$$az$ dan $$$bz$ - koefisien dekomposisi orthocenter atas dasar $$$A, B$ (bobot barycentric).

Gramian lengkap $$$Gm$ Itu terlihat seperti ini:

$$$Gm = \ mulai {bmatrix} 0 & za & zb \\ 1 & 0 & g_1 \\ 1 & g_2 & 0 \ end {bmatrix}$

Ini tupelnya $$$[za, zb]$ dan $$$[1, 1]$ mencerminkan koordinat ganda dari vektor nol. Koordinat ini adalah annihilator dari Laplacian (ketika dikalikan dengan Laplacian mereka memberikan vektor nol - jangan dikacaukan dengan vektor nol!).

Untuk memecahkan masalah, kita perlu menemukan jumlah nilai-nilai gramian: $$$- (g_1 + g_2)$ .

Kami mempertimbangkan jumlah tidak diketahui: $$$rz, az, bz, za, zb, g_1, g_2$ - hanya 7 (ya, ya - untuk mengetahui nilai dari satu jarak yang tidak menguntungkan, kita perlu menghitung tujuh nilai tambahan lainnya). Ada dua koneksi terkenal di pintu masuk - $$$c_1$ dan $$$c_2$ . Identitas $$$Lm \ Gm = I$ akan memberikan 9 persamaan. Total 7 + 2 = 9, - semuanya menyatu (mengejutkan). Tetap hanya menyelesaikan sistem persamaan.

Untuk grafik dua node, solusinya (semua tidak diketahui) dapat diekspresikan dalam bentuk eksplisit. Kami memberikan ekspresi terbatas untuk jumlah yang menarik bagi kami. Kami memperkenalkan konsep konektivitas geometris umum - ini adalah kebalikan dari norma pusat orthogonal $$$gc = 1 / rz$ . Dimensinya bertepatan dengan dimensi tautan grafik. Untuk grafik dua node (dan dua koneksi), koneksi geometrik memiliki ekspresi yang bagus:

$$$gc = 1 / rz = (\ sqrt {c_1} + \ sqrt {c_2}) ^ 2$

Melalui koneksi ini, seseorang dapat mengekspresikan produk skalar dari node:

$$$g_1 = -gc \ sqrt {c_2}, \ quad g_2 = -gc \ sqrt {c_1}$

Anda dapat menerjemahkan produk skalar $$$g$ dalam jarak terarah $$$s$ (3):

$$$s_ {BA} = gc \ sqrt {c_ {AB}}; \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

Jarak komutatif yang diinginkan antara node ditentukan oleh jumlah:

$$$S (A, B) = s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad (4)$

Nenek telah tiba

Akhirnya Ekspresi (4) - ini adalah formula yang diinginkan.

Jarak antara simpul dari grafik dua node berbanding terbalik dengan akar kuadrat dari produk counter-link.

Anda dapat memuat buku teks sekolah dengan formula lain yang tidak berguna.

Jika koneksi sama, maka hasilnya bertepatan dengan jarak resistif dalam grafik tidak diarahkan:

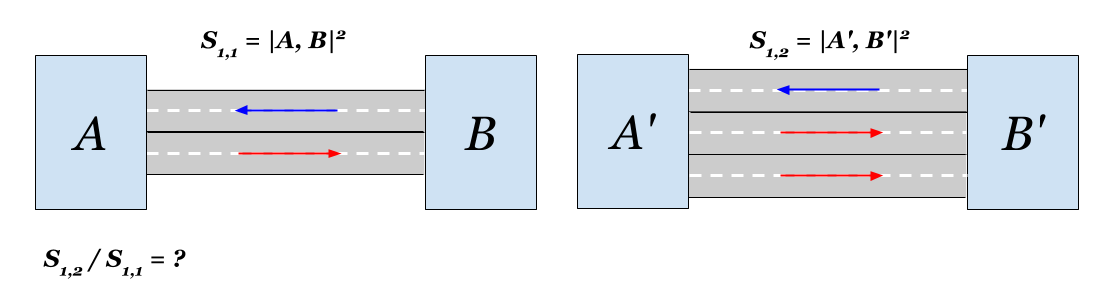
$$$S_ {c, c} (A, B) = 1 / c \ quad (4.1)$

Kami akan menghitung apa yang ada di kota kami. Jika Anda meletakkan jalur kedua, maka komunikasi satu arah akan berlipat ganda. Dengan demikian, jarak baru $$$S_ {1, 2} (A, B)$ dapat dinyatakan dalam bentuk aslinya:

$$$S_ {1, 2} (A, B) = 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1, 1} (A, B)$

Jarak antar area akan berkurang $$$\ sqrt {2}$ kali. Itu sudah jelas, bukan?

Juga ternyata dalam hal jarak, menambahkan satu jalur ke setiap jalan dua jalur di setiap sisi sama dengan menambahkan tiga jalur di satu sisi. Kedekatan Euclidean dalam kedua kasus akan berlipat ganda. Menarik.



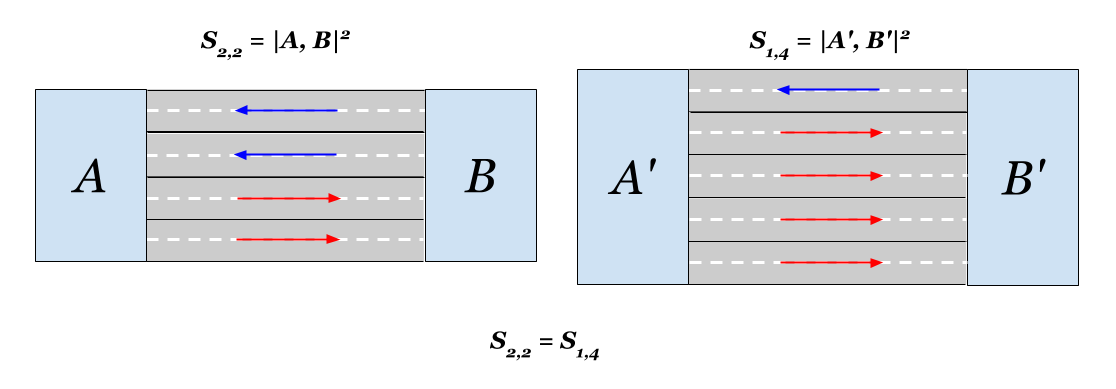
Itu saja. Terima kasih atas perhatian anda)