Dalam matematika, di mana pembuktian adalah segalanya, fakta juga penting. Namun, faktanya baik, hanya sementara modelnya bagus, dan membangun model adalah pekerjaan yang tidak bisa diandalkan. Jadi berapa banyak fakta yang cukup?

Bisakah Anda menemukan nomor berikutnya dalam urutan?
1, 2, 4, 8
Ini satu nomor lagi jika Anda membutuhkan lebih banyak data untuk membuat keputusan:
1, 2, 4, 8, 16
Nomor berikutnya harus 32, bukan? Polanya jelas: untuk menemukan nomor berikutnya, Anda harus menggandakan yang sebelumnya. 1 × 2 = 2; 2 × 2 = 4; 4 × 2 = 8; 8 × 2 = 16. Jadi, angka selanjutnya harus 16 × 2 = 32. Berapa banyak fakta yang diperlukan untuk mengonfirmasi hal ini?
Tetapi, meskipun masuk akal untuk menganggap bahwa angka berikutnya adalah 32, ini tidak selalu benar. Pertimbangkan urutan berikut: kita akan menghitung jumlah bagian di mana lingkaran dibagi dengan garis yang menghubungkan titik-titik yang terletak pada lingkaran.
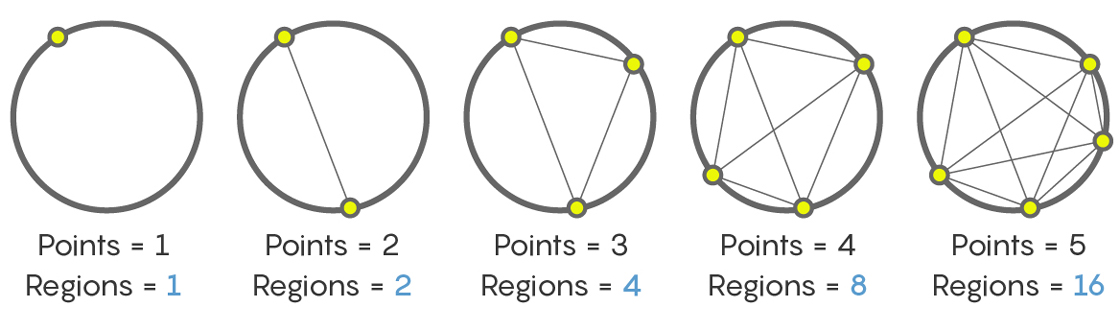
Satu titik memberikan satu bagian (seluruh bagian dalam lingkaran). Dua poin - dua bagian. Tiga poin - empat bagian. Lima dan enam masing-masing delapan dan enam belas. Hasilnya adalah urutan
1, 2, 4, 8, 16
Dan berapa banyak bagian yang akan muncul setelah menghubungkan garis enam titik pada lingkaran? Tidak ada yang akan menghukum Anda jika Anda, seperti banyak orang yang dihadapkan dengan tugas ini untuk pertama kalinya, mengatakan bahwa 32. Tapi ini tidak begitu. Bahkan, betapa pun menjengkelkannya, jawabannya adalah - 31! Hitung kembali diri Anda, lalu periksa kembali.
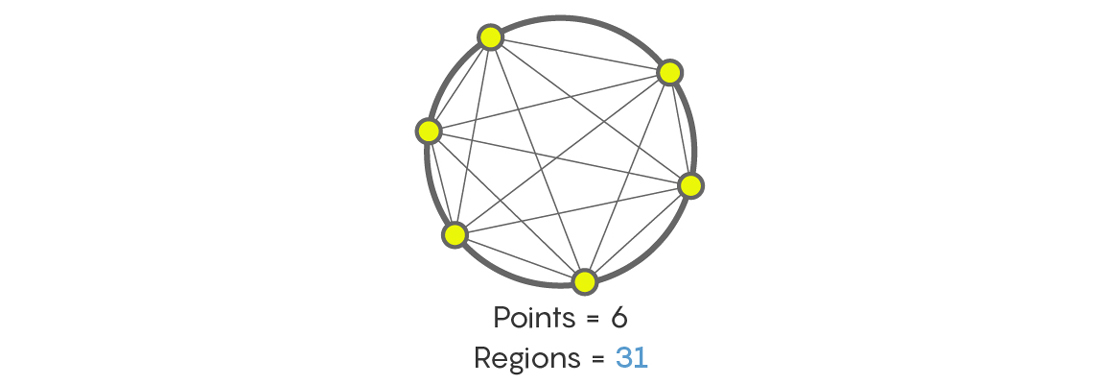
Tentu saja, ada urutan seperti 1, 2, 4, 8, 16, 32, 64, dan seterusnya, dari angka dua kali lipat setiap kali. Tetapi ada urutan lain, misalnya, jumlah maksimum bagian di mana lingkaran dibagi dengan garis-garis yang menghubungkan titik-titik pada lingkaran, dan ini adalah 1, 2, 4, 8, 16, 31, 57, 99, dan seterusnya. Memenuhi urutan 1, 2, 4, 8, 16, kita mungkin berpikir bahwa semua faktanya adalah bahwa angka berikutnya akan menjadi 32, tetapi mungkin ada sesuatu yang lain.
Matematika memiliki tradisi panjang yang menantang harapan kita dan membuat imajinasi kita berfungsi. Oleh karena itu, ahli matematika selalu berusaha untuk mendapatkan bukti yang kuat, bukan hanya fakta. Buktinya menetapkan kebenaran matematika. Semua fakta dapat menunjuk ke 32 sebagai angka berikutnya dalam urutan kami, tetapi tanpa bukti yang kuat kami tidak dapat memastikan hal itu.
Tapi tetap saja, fakta untuk ahli matematika bermanfaat dan penting. Sebelum membuktikan sesuatu, kita sering bermain dengan informasi yang tersedia, mempelajari masalahnya, mempertimbangkan contoh dan mengumpulkan data. Kami mempelajari dan menimbang fakta dan memutuskan apa yang harus dilakukan selanjutnya. Hasil ini membentuk pendapat kami, mengusulkan untuk membuktikan beberapa teorema dan menyangkal yang lain.
Hipotesis utama kembar adalah salah satu contoh di mana fakta mengendalikan pemikiran matematika kita dengan cara yang sama sebagai bukti. Bilangan prima kembar adalah pasangan bilangan prima yang berbeda 2 - misalnya, 3 dan 5, 11 dan 13, 101 dan 103. Hipotesis bilangan prima kembar menunjukkan bahwa tidak ada pasangan terbesar kembar seperti itu - yaitu, serupa pasangan terus-menerus muncul di garis angka ketika pindah ke tak terbatas.
Hipotesis utama kembar bukanlah teorema, karena, terlepas dari kenyataan bahwa ini adalah salah satu masalah paling terkenal dalam teori bilangan, belum ada yang bisa membuktikannya. Namun, hampir semua orang percaya bahwa itu benar, karena ada banyak fakta yang mendukungnya.
Misalnya, dalam pencarian kami untuk bilangan prima, kami terus-menerus menemukan pasangan bilangan prima kembar yang sangat besar. Masing-masing bilangan prima dari
pasangan terbesar yang
diketahui saat ini berisi 400.000 digit. Teorema yang mirip dengan hipotesis ini juga terbukti. Pada 2013,
Zhang Ethan mengejutkan komunitas matematika dengan membuktikan keberadaan sejumlah besar pasangan bilangan prima, berbeda tidak lebih dari 70 juta. Berkat proyek
Polymath terbuka yang mengikutinya, kita tahu bahwa ada jumlah pasang bilangan prima tak terbatas yang berbeda
tidak lebih dari 246 . Kami belum membuktikan keberadaan jumlah pasangan bilangan prima yang tak terbatas yang berbeda 2 - tetapi masih 2 lebih dekat dengan 246 dari 246 hingga tak terbatas.
Untuk alasan ini dan lainnya, kepercayaan pada keadilan, bahkan jika hipotesisnya tidak terbukti, tidak terlalu kontroversial. Namun, ada bidang matematika lain di mana fakta digunakan untuk membangun pendapat yang berubah menjadi lebih kontroversial.
Dalam studi kurva eliptik, peringkatnya, secara kasar, menunjukkan perkiraan numerik dari kompleksitas penyelesaian kurva ini. Selama bertahun-tahun diyakini bahwa
jajaran kurva eliptik tidak terbatas , yaitu, tidak ada batasan pada nilai pangkat kurva, atau pada kompleksitas solusi.
Namun, karya terbaru membuat matematikawan berpikir tentang kemungkinan peringkat terbatas. Makalah ini memberikan fakta yang menunjukkan bahwa ada kemungkinan bahwa ada sejumlah kurva terbatas yang peringkatnya lebih besar dari 21.
Namun, hati-hati disarankan. Fakta-fakta yang dikumpulkan oleh matematikawan tidak diambil dari dunia kurva eliptik - mereka berhubungan dengan matriks yang digunakan peneliti untuk memodelkan kurva. Model matematika banyak digunakan dalam sains, dan mereka bahkan dapat diputar ke dalam untuk mempelajari matematika itu sendiri. Ini adalah alat yang sangat kuat yang memungkinkan kita untuk mengganti tugas yang tidak bisa dipahami dengan tugas yang lebih mudah kita atasi.
Tetapi menggunakan model adalah bisnis yang sulit. Anda tidak pernah bisa yakin bahwa modelnya berperilaku sangat mirip dengan apa yang kita coba pahami, sehingga kita bisa menarik kesimpulan dari perilakunya. Juga, kita tidak dapat memastikan bahwa model kita persis sama di tempat-tempat yang paling penting. Oleh karena itu, sulit untuk memastikan bahwa fakta-fakta yang kami kumpulkan berdasarkan model benar-benar bersaksi tentang sifat nyata dari fenomena yang kita pelajari. Mari kita periksa masalah-masalah ini berdasarkan pada model sederhana dari hipotesis sederhana.
Bayangkan kita ingin mempelajari pernyataan berikut: setiap dua garis berpotongan atau paralel.
Yang kami maksud dengan persimpangan adalah adanya garis lurus di titik-titik yang sama, dan dengan paralelisme, fakta bahwa mereka bergerak dalam satu arah tetapi tidak berpotongan (konsep ini dapat didefinisikan secara berbeda, tetapi saya akan menggunakan ini untuk kesederhanaan).
Untuk mempelajari masalah ini, buat model. Setiap baris diwakili oleh persamaan dari garis miring, yang dapat Anda ingat dari kursus sekolah. Artinya, kita mengasumsikan bahwa setiap baris dapat dijelaskan oleh persamaan bentuk
y = mx + b
di mana m adalah kemiringan garis (kecuramannya), dan b adalah titik persimpangan sumbu y (sumbu vertikal).
Memodelkan garis dengan cara ini nyaman untuk percobaan pada mereka. Model ini memungkinkan kita untuk membuat garis acak dengan memilih sepasang angka acak, m dan b. Kita dapat memilih sepasang garis acak dan memeriksanya - apakah mereka berpotongan? Apakah mereka pergi satu arah? Apakah ada hal lain yang terjadi?
Berikut ini beberapa contoh hasil percobaan tersebut.
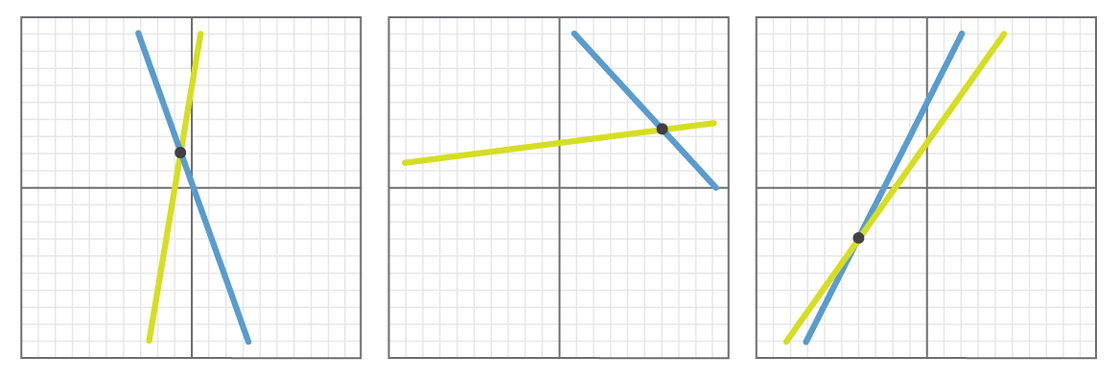
Dalam setiap contoh, garis yang dipilih secara acak berpotongan. Jika kita melakukan percobaan ini ribuan kali - atau 10.000, atau satu juta - kita akan menemukan bahwa dalam semua kasus garis akan berpotongan atau paralel (dan kemungkinan besar, semua garis akan berpotongan, karena tidak mungkin kedua garis memiliki kemiringan yang sama, dipilih secara kebetulan).
Oleh karena itu, dengan melihat jutaan contoh, Anda dapat sampai pada kesimpulan bahwa hipotesis tersebut kemungkinan besar benar. Semua fakta sepenuhnya mendukung pernyataan bahwa setiap pasangan garis paralel atau berpotongan.
Namun, faktanya hanya sebaik modelnya bagus, dan pemodelannya berbahaya. Mari kita lihat bahaya apa yang kita buat untuk diri kita sendiri dalam contoh kita.
Satu masalah adalah bahwa jenis garis tertentu akan lebih umum daripada yang lain. Berikut ini adalah grafik yang menunjukkan 50 garis dengan b = 0 dan 0 ≤ m ≤ 1.
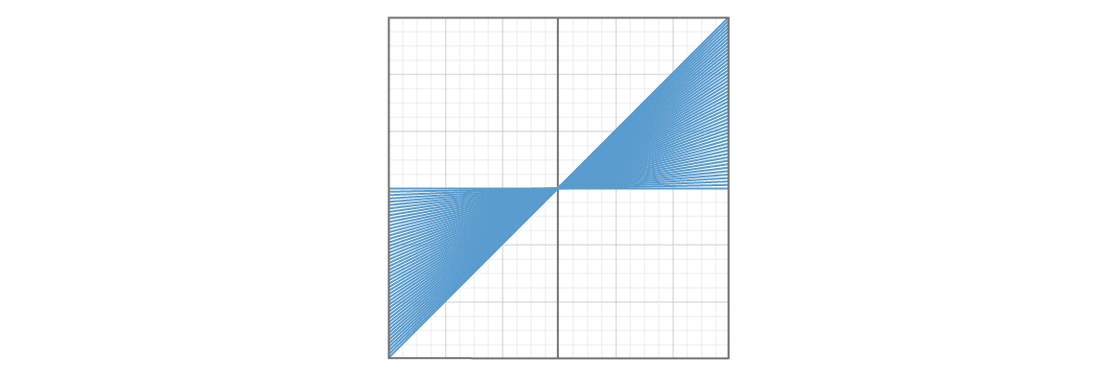
Dan di sini adalah grafik yang menunjukkan 50 garis dengan b = 0 dan m ≥ 1.

Sepertinya seperempat pesawat ditutupi dengan garis lurus dengan kemiringan dari 0 hingga 1, dan seperempat lainnya ditutupi dengan garis lurus dengan kemiringan lebih besar dari 1. Memilih angka lebih besar dari 1 tampaknya lebih mungkin daripada memilih angka dari 0 hingga 1, sehingga garis lurus lebih mungkin terjadi akan berada di bagian kedua pesawat. Ini berarti bahwa garis-garis tertentu, dengan kemiringan dari 0 hingga 1, akan sangat sedikit terwakili dalam model. Dan jika beberapa hal aneh terjadi di bagian pesawat ini dengan garis lurus, model kita tidak mungkin memberi tahu kita tentang hal ini.
Jika Anda melihat dekat pada grafik kedua, kita akan melihat masalah lain. Semakin besar m, semakin curam garis lurus. Garis lurus paling keren adalah vertikal. Apa kemiringan garis vertikal? Menurut definisi, itu tidak didefinisikan: tidak ada angka m yang dapat menggambarkan garis vertikal. Ternyata tidak ada garis vertikal dalam model kami, dan kami tidak dapat bereksperimen dengannya. Kami belum mulai mengumpulkan fakta, tetapi sudah mengesampingkan beberapa kasus khusus hanya karena skema pembangunan model.
Hal yang sama menyangkut masalah paling serius dari model kami. Orang-orang yang dengan mudah membayangkan ruang tiga dimensi mungkin segera menyadari bahwa hipotesis kami salah. Garis lurus tidak harus berpotongan atau paralel. Bayangkan dua koridor menuju ke arah yang berbeda di lantai bangunan yang berbeda. Ini adalah garis lurus berpotongan - garis lurus yang tidak berpotongan dan tidak paralel.
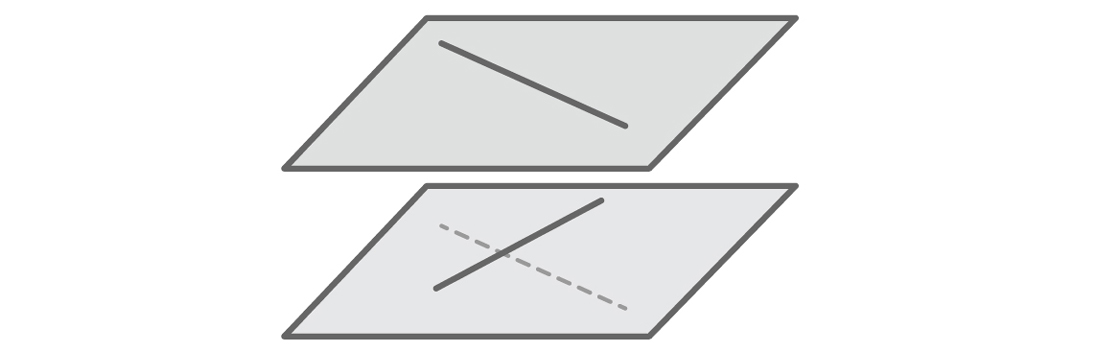
Garis silang harus terletak pada bidang yang berbeda. Tetapi karena model kita mendefinisikan garis apa saja melalui persamaan y = mx + b, kita secara otomatis membayangkan bahwa semua garis berada dalam bidang yang sama. Model kami hanya akan memberikan fakta yang mendukung hipotesis kami, karena jika dua garis terletak pada bidang yang sama, mereka benar-benar harus berpotongan atau berjalan paralel. Kami tidak akan melihat fakta lain: tidak ada garis berpotongan dalam model kami. Seperti dalam kasus garis vertikal, model mengesampingkan apa yang tidak dapat kita bayangkan.
Ini adalah contoh sederhana menggunakan model bodoh dengan banyak masalah, termasuk pertanyaan rumit, seperti prosedur untuk memilih angka acak dari set yang tak terbatas. Matematikawan profesional yang mempelajari jajaran kurva eliptik tidak akan pernah melakukan kesalahan yang disederhanakan dan jelas.
Matematikawan ini tahu tindakan pencegahan apa yang harus diambil ketika bekerja dengan model. Mereka tahu bahwa, terlepas dari seberapa berguna dan menarik model itu, atau seberapa meyakinkan fakta yang dikumpulkan akan, kurva eliptik dapat mengungkapkan sifat-sifat yang tidak mereka bayangkan. Dan jika ini tidak dapat dibayangkan, model Anda tidak akan mempertimbangkan ini, dan, oleh karena itu, faktanya tidak akan tercermin.
Tetapi apakah model baru itu benar atau tidak, itu memaksa matematikawan untuk berpikir secara produktif tentang kurva elips. Jika itu benar-benar mencerminkan kebenaran, maka ide-ide dari dunia matriks dapat menjelaskan perilaku kurva. Jika tidak, memahami mengapa kurva elips tidak dapat dimodelkan dengan cara ini dapat menyebabkan pemahaman yang lebih baik tentang masalah tersebut. Fakta-fakta yang kami kumpulkan dapat mendekatkan kita pada bukti, dengan satu atau lain cara.