Lapisan Konvolusi: Teknik Optimalisasi Penggandaan Matriks

Pendahuluan

Artikel ini merupakan kelanjutan dari serangkaian artikel yang menggambarkan algoritma yang mendasarinya.
Synet adalah kerangka kerja untuk meluncurkan jaringan saraf pra-terlatih pada CPU.

Jika Anda melihat distribusi waktu prosesor yang dihabiskan untuk propagasi sinyal langsung di jaringan saraf, ternyata seringkali lebih dari 90% dari semua waktu dihabiskan di lapisan convolutional. Oleh karena itu, jika kita ingin mendapatkan algoritma cepat untuk jaringan saraf, kita perlu, pertama-tama, algoritma cepat untuk lapisan convolutional. Pada artikel ini, saya ingin menjelaskan metode untuk mengoptimalkan propagasi sinyal langsung dalam lapisan convolutional. Dan saya ingin memulai dengan metode yang paling banyak digunakan berdasarkan perkalian matriks. Saya akan mencoba untuk menjaga presentasi dalam bentuk yang paling mudah diakses sehingga artikel ini menarik tidak hanya untuk spesialis (mereka sudah tahu segalanya tentang itu), tetapi juga untuk kalangan pembaca yang lebih luas. Saya tidak berpura-pura menjadi ulasan lengkap, jadi setiap komentar dan tambahan hanya diterima.

Opsi Lapisan Konvolusi

Saya ingin memulai deskripsi dengan deskripsi parameter yang ada di lapisan convolutional. Para ahli dapat melewati bagian ini dengan aman.

Input dan Output Ukuran Gambar

Pertama-tama, lapisan konvolusional ditandai oleh input dan gambar output, yang dicirikan oleh parameter berikut:

• srcC / dstC - jumlah saluran dalam gambar input dan output. Notasi alternatif: C / D.
• srcH / dstH - tinggi dari gambar input dan output. Penunjukan alternatif: H.
• srcW / dstW - lebar dari gambar input dan output. Penunjukan alternatif: W.
• batch - jumlah input (output) gambar - layer dapat memproses seluruh batch gambar sekaligus. Penunjukan alternatif: N.

Ukuran Inti Konvolusi

Operasi konvolusi secara inheren merupakan jumlah terbobot dari lingkungan tertentu pada titik tertentu dalam gambar. Ukuran kernel konvolusi - mencirikan ukuran lingkungan ini dan dijelaskan oleh dua parameter:

• kernelY adalah ketinggian kernel konvolusi. Penunjukan alternatif: Y.
• kernelX adalah lebar kernel konvolusi. Penunjukan alternatif: X.

Konvolusi yang paling umum dengan ukuran kernel 1x1 dan 3x3 . Ukuran 5x5 dan 7x7 jauh lebih jarang. Ukuran konvolusi besar, serta konvolusi dengan kernel selain kuadrat, juga kadang-kadang ditemukan, tetapi ini lebih eksotis.

Langkah konvolusi

Parameter penting lainnya adalah langkah konvolusi:

• langkahnya adalah langkah konvolusi vertikal.
• strideX - langkah konvolusi horizontal.

Jika langkahnya berbeda dari 1x1 , misalnya - 2x2 , maka gambar output akan menjadi setengahnya (konvolusi akan dihitung hanya di lingkungan titik genap).

Peregangan Konvolusi

Kernel konvolusi dapat diregangkan (menambah ukuran jendela efektif, sambil mempertahankan jumlah operasi) menggunakan parameter berikut:

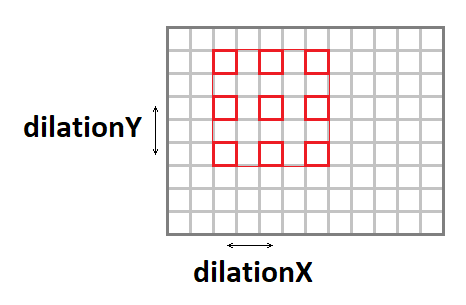
• dilationY - peregangan konvolusi vertikal.
• dilationX - peregangan konvolusi horizontal.

Perlu dicatat bahwa kasus dengan peregangan selain 1x1 cukup jarang (saya belum pernah mengalami hal seperti itu dalam karir saya).

Gambar Input Padding

Jika Anda menerapkan konvolusi dengan jendela yang berbeda dari satu ke gambar, maka gambar keluaran akan lebih sedikit dengan jumlah kernel - 1 . Bundel itu, seolah-olah, "memakan" ujung-ujungnya. Untuk mempertahankan ukuran gambar, gambar input sering kali diisi di sekitar tepi dengan angka nol. Empat parameter lagi bertanggung jawab untuk ini:

• padY / padX - padding depan vertikal dan horizontal.
• padH / padW - padding belakang vertikal dan horizontal.

Grup saluran

Biasanya, setiap saluran output adalah jumlah dari konvolusi di semua saluran input. Namun, ini tidak selalu terjadi. Dimungkinkan untuk membagi saluran input dan output ke dalam grup, penjumlahan hanya dilakukan di dalam grup:

• grup - jumlah grup.

Dalam praktiknya, situasi dengan grup = 1 dan grup = srcC = dstC , yang disebut konvolusi mendalam, paling sering dijumpai.

Fungsi perpindahan dan aktivasi

Meskipun fungsi perpindahan dan aktivasi secara formal tidak termasuk dalam konvolusi, tetapi sangat sering kedua operasi ini mengikuti lapisan konvolusional, mengapa mereka biasanya juga termasuk di dalamnya. Mengingat berbagai kemungkinan fungsi aktivasi dan parameternya, saya tidak akan menjelaskannya di sini secara rinci.

Implementasi dasar dari algoritma

Untuk mulai dengan, saya ingin memberikan implementasi dasar dari algoritma:

float relu(float value) { return value > 0 ? return value : 0; } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int b = 0; b < batch; ++b) { for (int g = 0; g < group; ++g) { for (int dc = 0; dc < dstC / group; ++dc) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { float sum = 0; for (int sc = 0; sc < srcC / group; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) sum += src[((b * srcC + sc)*srcH + sy)*srcW + sx] * weight[((dc * srcC / group + sc)*kernelY + ky)*kernelX + kx]; } } } dst[((b * dstC + dc)*dstH + dy)*dstW + dx] = relu(sum + bias[dc]); } } } } } } 

Dalam implementasi ini, saya berasumsi bahwa gambar input dan output dalam format NCHW :



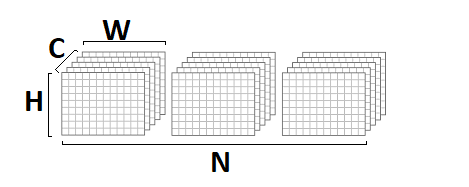
bobot konvolusi disimpan dalam format DCYX , dan fungsi aktivasi kami adalah ReLU . Dalam kasus umum, ini tidak begitu, tetapi untuk implementasi dasar, asumsi seperti itu cukup tepat - Anda harus mulai dari sesuatu.

Kami memiliki 8 siklus bersarang dan jumlah operasi:

 batch * kernelY * kernelX * srcC * dstH * dstW * dstC / group * 2, 

sedangkan jumlah data yang di input:

 batch * srcC * srcH * srcW, 

dan gambar output:

 batch * dstC * dstH * dstW, 

dan jumlah bobot:

 kernelY * kernelX * srcC * dstC / group. 

Jika grup << srcC (jumlah grup jauh lebih kecil dari jumlah saluran), serta dengan parameter srcC , srcH , srcW , dan dstC yang cukup besar, kami mendapatkan masalah komputasi klasik ketika jumlah perhitungan secara signifikan melebihi jumlah input dan data output. Yaitu operasi konvolusi dengan implementasi yang tepat harus bertumpu pada sumber daya komputasi prosesor, dan bukan pada bandwidth memori. Tetap hanya untuk menemukan implementasi ini.

Pengurangan masalah untuk perkalian matriks

Operasi utama dalam konvolusi adalah untuk mendapatkan jumlah yang tertimbang, dan bobotnya sama untuk semua titik pada gambar output. Jika Anda mengatur ulang gambar input sebagai berikut:

 void im2col(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int sc = 0; sc < srcC; ++sc) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[((b * srcC + sc)*srcH + sy)*srcW + sx]; else *buf++ = 0; } } } } } } 

Kemudian kita akan beralih dari format srcC - srcH - srcW kita akan beralih ke format srcC - kernelY - kernelX - dstH - dstW . Gambar di bawah ini menunjukkan bagaimana gambar dikonversi dengan inti padding 1 dan 3x3 :



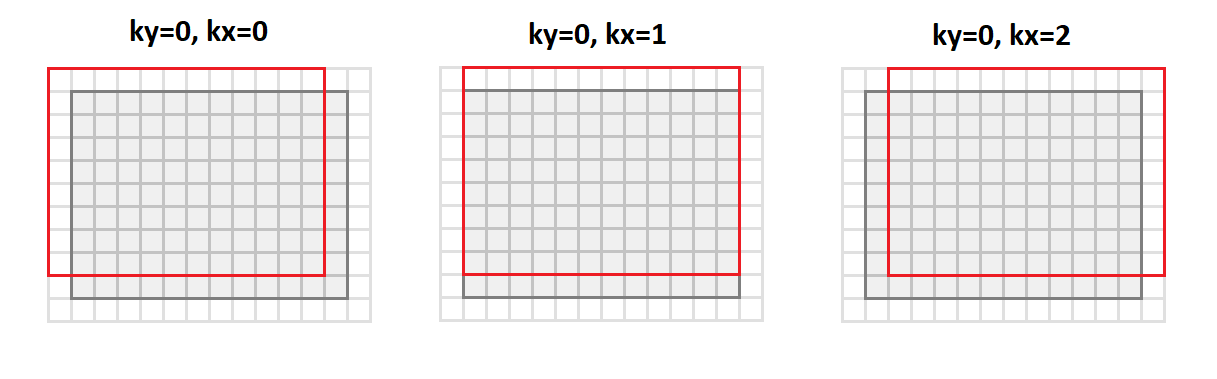
Dalam hal ini, semua titik lingkungan gambar yang diperlukan untuk operasi konvolusi disejajarkan di sepanjang kolom dari matriks yang dihasilkan (oleh karena itu namanya adalah usia untuk dikoleksi).

Representasi baru dari gambar input menarik karena sekarang operasi konvolusi pada kita direduksi menjadi perkalian matriks:



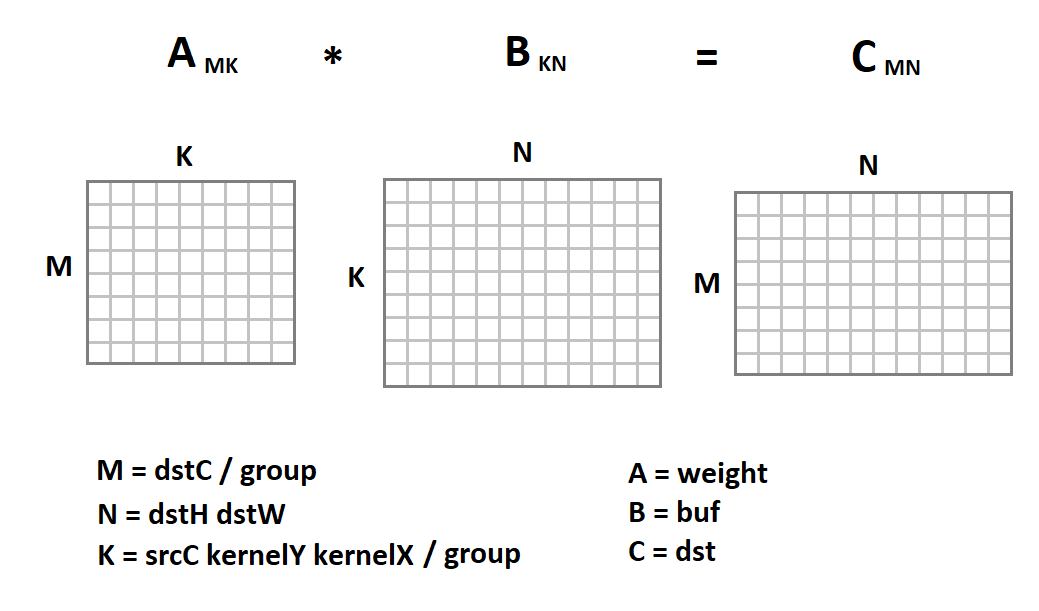
Sekarang kode konvolusi akan terlihat seperti ini:

 void gemm_nn(int M, int N, int K, float alpha, const float * A, int lda, float beta, const float * B, int ldb, float * C, int ldc) { for (int i = 0; i < M; ++i) { for (int j = 0; j < N; ++j) { C[i*ldc + j] = beta; for (int k = 0; k < K; ++k) C[i*ldc + j] += alpha * A[i*lda + k] * B[k*ldb + j]; } } } void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstC / group; int N = dstH * dstW; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2col(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, weight + M * K * g, K, 0, buf + N * K * g, N, dst + M * N * g, N)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Di sini implementasi sederhana dari perkalian matriks diberikan hanya sebagai contoh. Kami dapat menggantinya dengan implementasi lainnya. Untungnya, perkalian matriks adalah operasi lama yang telah diimplementasikan di banyak perpustakaan dengan efisiensi sangat tinggi (hingga 90% dari kinerja CPU yang secara teori memungkinkan). Pada topik bagaimana efisiensi ini dicapai, saya bahkan memiliki artikel terpisah .

Menggunakan perkalian matriks untuk format NHWC

Seiring dengan format NCHW , NHWC sering digunakan dalam pembelajaran mesin:



Sebagai contoh, perhatikan bahwa NHWC adalah format Tensorflow asli.

Perlu dicatat bahwa untuk format ini, operasi konvolusi juga dapat menyebabkan multiplikasi matriks. Untuk melakukan ini, dari format srcH - srcW - srcC kami menerjemahkan gambar asli ke dalam format dstH - dstW - kernelY - kernelX - srcC menggunakan fungsi im2row :

 void im2row(const float * src, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; for (int g = 0; g < group; ++g) { for (int dy = 0; dy < dstH; ++dy) { for (int dx = 0; dx < dstW; ++dx) { for (int ky = 0; ky < kernelY; ky++) { for (int kx = 0; kx < kernelX; kx++) { int sy = dy * strideY + ky * dilationY - padY; int sx = dx * strideX + kx * dilationX - padX; for (int sc = 0; sc < srcC; ++sc) { if (sy >= 0 && sy < srcH && sx >= 0 && sx < srcW) *buf++ = src[(sy * srcW + sx)*srcC + sc]; else *buf++ = 0; } } } } } src += srcC / group; } } 

Selain itu, semua titik lingkungan gambar yang diperlukan untuk operasi konvolusi disejajarkan di sepanjang baris matriks yang dihasilkan (karenanya namanya - usia ke baris s). Kita juga harus mengubah format penyimpanan skala konvolusi dari format DCYX ke format YXCD . Sekarang kita bisa menerapkan perkalian matriks:



Berbeda dengan format NCHW , kami mengalikan matriks gambar dengan matriks bobot, dan bukan sebaliknya. Berikut ini adalah kode fungsi konvolusi:

 void convolution(const float * src, int batch, int srcC, int srcH, int srcW, int kernelY, int kernelX, int dilationY, int dilationX, int strideY, int strideX, int padY, int padX, int padH, int padW, int group, const float * weight, const float * bias, float * dst, int dstC, float * buf) { int dstH = (srcH + padY + padH - (dilationY * (kernelY - 1) + 1)) / strideY + 1; int dstW = (srcW + padX + padW - (dilationX * (kernelX - 1) + 1)) / strideX + 1; int M = dstH * dstW; int N = dstC / group; int K = srcC * kernelY * kernelX / group; for (int b = 0; b < batch; ++b) { im2row(src, srcC, srcH, srcW, kernelY, kernelX, dilationY, dilationY, strideY, strideX, padY, padX, padH, padW, group, buf); for (int g = 0; g < group; ++g) gemm_nn(M, N, K, 1, buf + M * K * g, K * group, 0, weight + N * g, dstC, dst + N * g, dstC)); for (int i = 0; i < M; ++i) for (int j = 0; j < N; ++j) dst[i*N+ j] = relu(dst[i*N + j] + bias[i]); src += srcC*srcH*srcW; dst += dstC*dstH*dstW; } } 

Keuntungan dan kerugian dari metode ini

Dari awal, saya ingin membuat daftar keuntungan dari pendekatan ini:

• Metode ini memiliki implementasi yang sangat sederhana. Bukan untuk apa-apa yang digunakan di hampir semua perpustakaan yang saya tahu.
• Efektivitas metode untuk banyak kasus sangat tinggi: dari unit persen dalam versi dasar kami mencapai lebih dari 80% dari maksimum teoritis.
• Pendekatannya bersifat universal - kami memiliki satu kode untuk semua parameter yang mungkin dari lapisan konvolusional (dan ada banyak dari mereka!). Oleh karena itu, metode ini sering bekerja dalam kasus-kasus di mana pendekatan yang lebih efektif (dan karenanya lebih terspesialisasi) memiliki keterbatasan.
• Pendekatan ini berfungsi untuk format utama tensor gambar - NCHW dan NHWC .

Sekarang tentang kerugiannya:

• Sayangnya, penggandaan matriks standar efektif asalkan nilai-nilai parameter M, N, K cukup besar dan, apalagi, mereka kira-kira urutan besarnya yang sama (efisiensi didasarkan pada kenyataan bahwa jumlah perhitungan yang diperlukan adalah ~ O (N ^ 3) , dan throughput yang diperlukan kemampuan memori ~ O (N ^ 2) ). Oleh karena itu, jika salah satu parameter M, N, K kecil, efisiensi metode turun tajam.
• Metode ini memerlukan konversi data input. Dan ini jauh dari operasi gratis. Dia hanya bisa diabaikan jika K cukup besar. Dan jika kita memperhitungkan bahwa di dalam perkalian matriks standar masih ada transformasi internal dari data input, maka situasinya menjadi lebih menyedihkan.
• Berdasarkan fakta bahwa K = srcC * kernelY * kernelX / group , efisiensi metode ini sangat rendah untuk lapisan konvolusional input. Dan untuk konvolusi yang mendalam, metode matriks umumnya kalah dari implementasi sepele.
• Metode ini membutuhkan pemrosesan tambahan dari data output untuk operasi shift dan perhitungan fungsi aktivasi.
• Ada metode matematika yang lebih efisien untuk menghitung konvolusi, yang membutuhkan operasi lebih sedikit.

Kesimpulan

Metode penghitungan konvolusi berdasarkan perkalian matriks mudah diterapkan dan memiliki efisiensi tinggi. Sayangnya, ini tidak universal. Untuk sejumlah kasus khusus, ada pendekatan yang lebih cepat, uraian yang ingin saya tunda untuk artikel selanjutnya dari seri ini. Menunggu umpan balik dan komentar dari pembaca. Saya harap Anda tertarik!

PS Ini dan pendekatan lainnya diterapkan oleh saya dalam Kerangka Konvolusi sebagai bagian dari perpustakaan Simd .
Kerangka kerja ini mendasari Synet , kerangka kerja untuk menjalankan jaringan saraf pra-terlatih pada CPU.