Kata Pengantar
Belum lama ini saya harus bekerja dengan menyederhanakan rantai poligon (
proses yang memungkinkan untuk mengurangi jumlah titik polyline ). Secara umum, jenis tugas ini sangat umum ketika memproses grafik vektor dan ketika membangun peta. Sebagai contoh, kita dapat mengambil rantai yang beberapa titiknya jatuh ke piksel yang sama - jelas bahwa semua titik ini dapat disederhanakan menjadi satu. Beberapa waktu yang lalu, saya praktis tidak tahu apa-apa tentang ini dari kata "sepenuhnya", dan karena itu, saya harus dengan cepat mengisi pengetahuan yang diperlukan tentang topik ini. Tapi apa yang mengejutkan saya ketika saya tidak menemukan manual yang cukup lengkap di Internet di Internet ... Saya harus mencari kutipan untuk informasi dari sumber yang sama sekali berbeda dan, setelah analisis, membangun semuanya menjadi gambaran besar. Jujur bukan pekerjaan yang paling menyenangkan. Oleh karena itu, saya ingin menulis serangkaian artikel tentang algoritma penyederhanaan rantai poligonal. Saya baru saja memutuskan untuk memulai dengan algoritma Douglas-Pecker paling populer.
Deskripsi
Algoritme menetapkan polyline awal dan jarak maksimum (ε), yang dapat antara polyline asli dan yang disederhanakan (yaitu, jarak maksimum dari titik asli ke bagian terdekat dari polyline yang dihasilkan). Algoritma secara rekursif membagi polyline. Input ke algoritma adalah koordinat semua titik antara yang pertama dan terakhir, termasuk mereka, serta nilai ε. Poin pertama dan terakhir tidak berubah. Setelah itu, algoritma menemukan titik terjauh dari segmen yang terdiri dari yang pertama dan terakhir (
algoritma pencarian adalah jarak dari titik ke segmen ). Jika titik terletak pada jarak kurang dari ε, maka semua titik yang belum ditandai untuk penyimpanan dapat dikeluarkan dari set, dan garis lurus yang dihasilkan memperhalus kurva dengan akurasi setidaknya ε. Jika jarak ini lebih besar dari ε, maka algoritma secara rekursif menyebut dirinya pada set dari titik awal ke yang diberikan dan dari yang diberikan ke titik akhir.
Perlu dicatat bahwa algoritma Douglas-Pecker tidak mempertahankan topologi dalam pekerjaannya. Ini berarti bahwa sebagai hasilnya, kita bisa mendapatkan garis dengan persimpangan diri. Sebagai contoh ilustratif, ambil polyline dengan set poin berikut: [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] dan lihat proses penyederhanaan untuk nilai ε yang berbeda:
Polyline asli dari kumpulan poin yang disajikan:

Polyline dengan ε sama dengan 0,5:
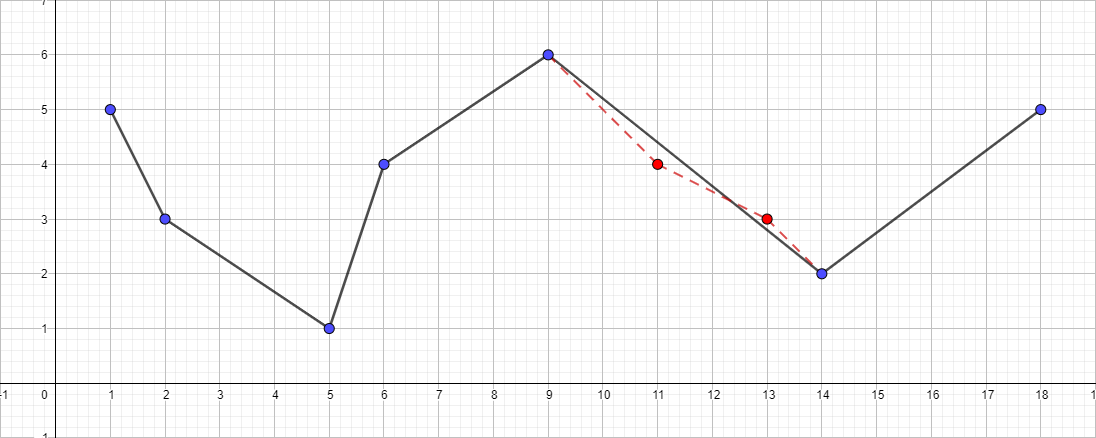
Polyline dengan ε sama dengan 1:

Polyline dengan ε sama dengan 1,5:
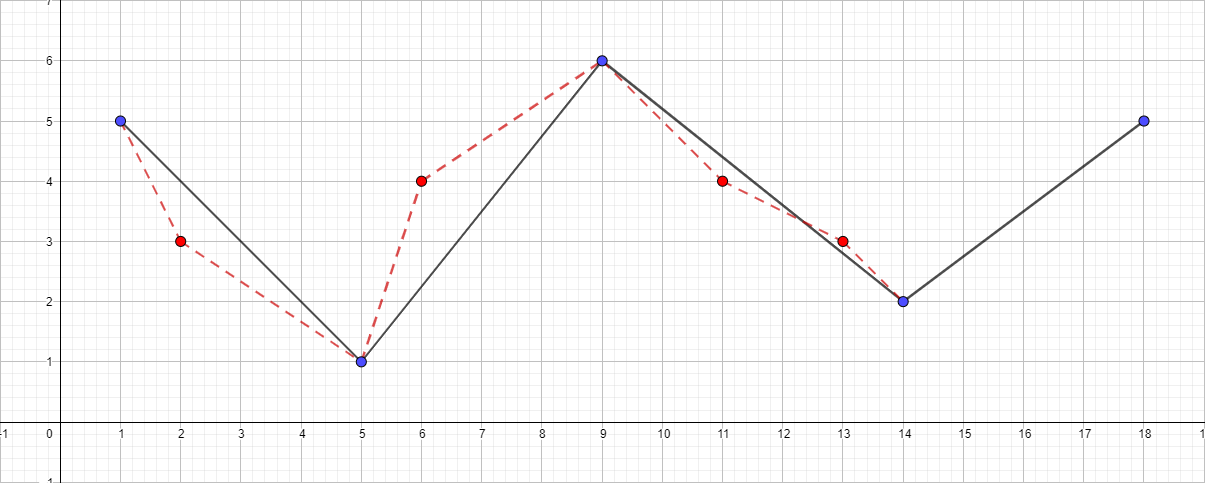
Anda dapat terus meningkatkan jarak maksimum dan memvisualisasikan algoritma, tetapi, saya pikir, poin utama setelah contoh-contoh ini menjadi jelas.
Implementasi
C ++ dipilih sebagai bahasa pemrograman untuk implementasi algoritma, kode sumber lengkap dari algoritma yang dapat Anda lihat di
sini . Dan sekarang langsung ke implementasinya sendiri:
#define X_COORDINATE 0 #define Y_COORDINATE 1 template<typename T> using point_t = std::pair<T, T>; template<typename T> using line_segment_t = std::pair<point_t<T>, point_t<T>>; template<typename T> using points_t = std::vector<point_t<T>>; template<typename CoordinateType> double get_distance_between_point_and_line_segment(const line_segment_t<CoordinateType>& line_segment, const point_t<CoordinateType>& point) noexcept { const CoordinateType x = std::get<X_COORDINATE>(point); const CoordinateType y = std::get<Y_COORDINATE>(point); const CoordinateType x1 = std::get<X_COORDINATE>(line_segment.first); const CoordinateType y1 = std::get<Y_COORDINATE>(line_segment.first); const CoordinateType x2 = std::get<X_COORDINATE>(line_segment.second); const CoordinateType y2 = std::get<Y_COORDINATE>(line_segment.second); const double double_area = abs((y2-y1)*x - (x2-x1)*y + x2*y1 - y2*x1); const double line_segment_length = sqrt(pow((x2-x1), 2) + pow((y2-y1), 2)); if (line_segment_length != 0.0) return double_area / line_segment_length; else return 0.0; } template<typename CoordinateType> void simplify_points(const points_t<CoordinateType>& src_points, points_t<CoordinateType>& dest_points, double tolerance, std::size_t begin, std::size_t end) { if (begin + 1 == end) return; double max_distance = -1.0; std::size_t max_index = 0; for (std::size_t i = begin + 1; i < end; i++) { const point_t<CoordinateType>& cur_point = src_points.at(i); const point_t<CoordinateType>& start_point = src_points.at(begin); const point_t<CoordinateType>& end_point = src_points.at(end); const double distance = get_distance_between_point_and_line_segment({ start_point, end_point }, cur_point); if (distance > max_distance) { max_distance = distance; max_index = i; } } if (max_distance > tolerance) { simplify_points(src_points, dest_points, tolerance, begin, max_index); dest_points.push_back(src_points.at(max_index)); simplify_points(src_points, dest_points, tolerance, max_index, end); } } template< typename CoordinateType, typename = std::enable_if<std::is_integral<CoordinateType>::value || std::is_floating_point<CoordinateType>::value>::type> points_t<CoordinateType> duglas_peucker(const points_t<CoordinateType>& src_points, double tolerance) noexcept { if (tolerance <= 0) return src_points; points_t<CoordinateType> dest_points{}; dest_points.push_back(src_points.front()); simplify_points(src_points, dest_points, tolerance, 0, src_points.size() - 1); dest_points.push_back(src_points.back()); return dest_points; }
Sebenarnya penggunaan algoritma itu sendiri:
int main() { points_t<int> source_points{ { 1, 5 }, { 2, 3 }, { 5, 1 }, { 6, 4 }, { 9, 6 }, { 11, 4 }, { 13, 3 }, { 14, 2 }, { 18, 5 } }; points_t<int> simplify_points = duglas_peucker(source_points, 1); return EXIT_SUCCESS; }
Contoh eksekusi algoritma
Sebagai input, kami mengambil set poin yang sebelumnya diketahui [{1; 5}, {2; 3}, {5; 1}, {6; 4}, {9; 6}, {11; 4}, {13; 3}, {14; 2}, {18; 5}] dan ε sama dengan 1:
- Temukan titik terjauh dari segmen {1; 5} - {18; 5}, titik ini akan menjadi titik {5; 1}.
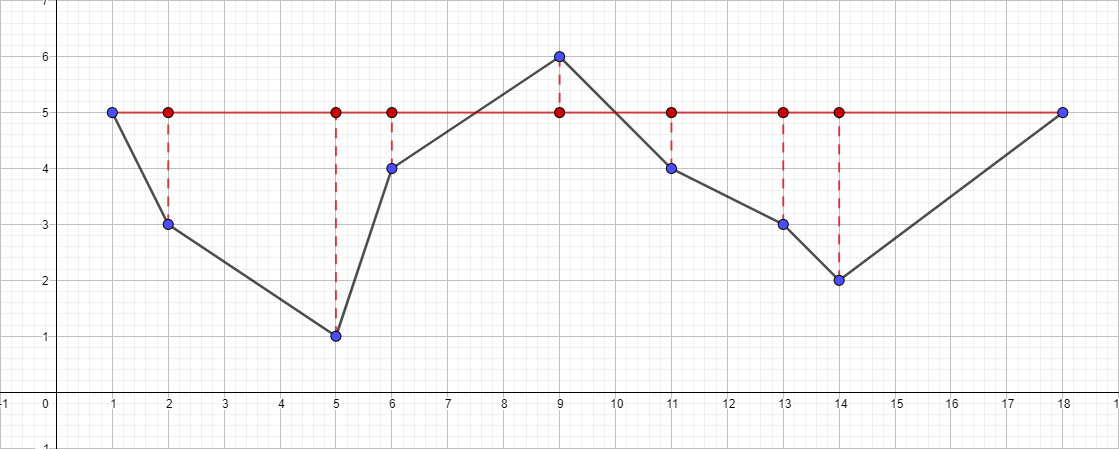
- Periksa jaraknya ke segmen {1; 5} - {18; 5}. Ternyata lebih dari 1, yang berarti kami menambahkannya ke polyline yang dihasilkan.
- Jalankan secara rekursif algoritma untuk segmen {1; 5} - {5; 1} dan temukan titik paling jauh untuk segmen ini. Poin ini adalah {2; 3}.
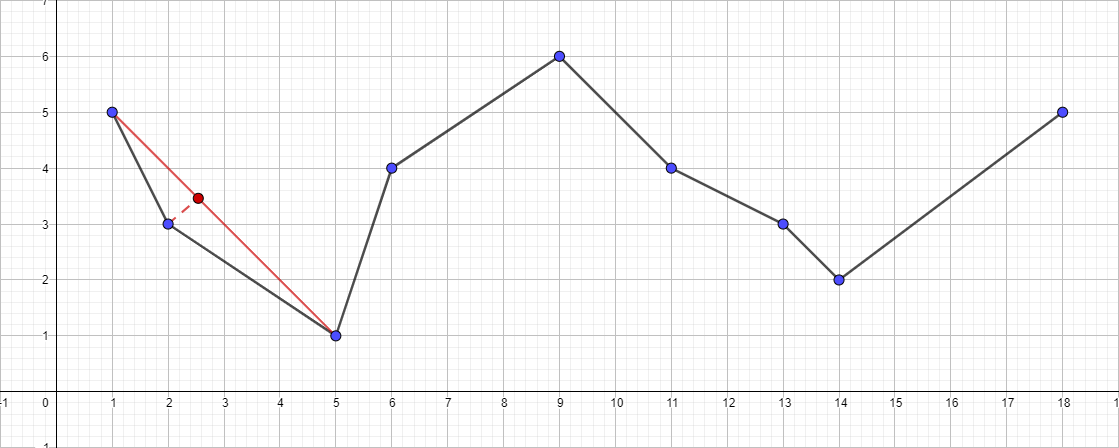
- Periksa jaraknya ke segmen {1; 5} - {5; 1}. Dalam hal ini, kurang dari 1, yang berarti kita dapat dengan aman membuang poin ini.
- Jalankan secara rekursif algoritma untuk segmen {5; 1} - {18; 5} dan temukan titik paling jauh untuk segmen ini ...
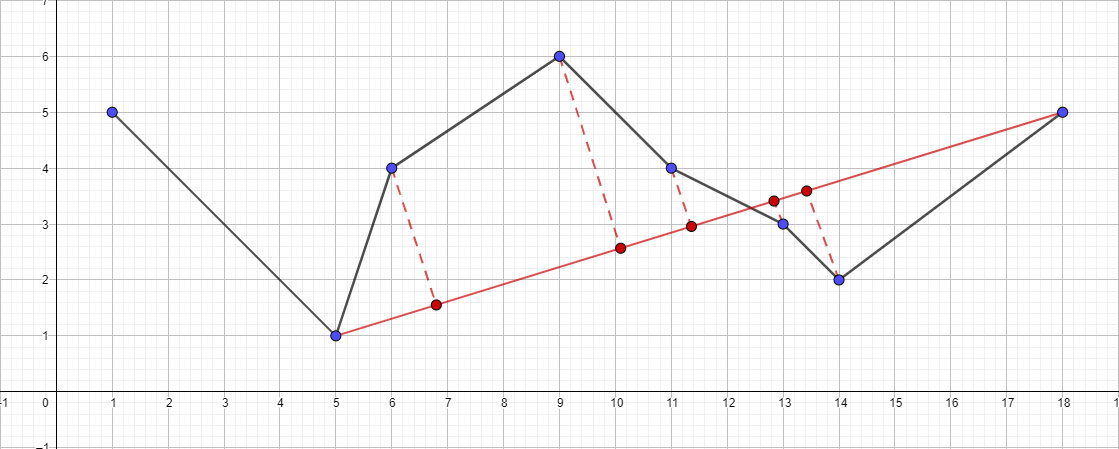
- Dan seterusnya sesuai dengan rencana yang sama ...
Akibatnya, pohon panggilan rekursif untuk data tes ini akan terlihat seperti ini:
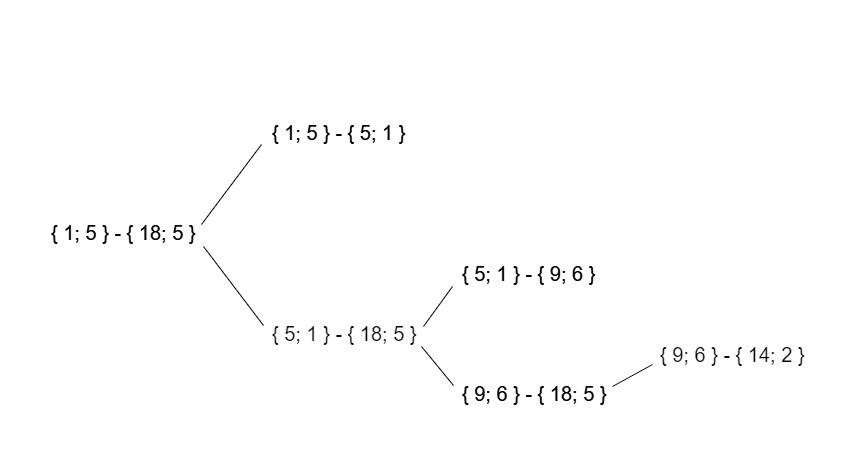
Waktu kerja
Kompleksitas yang diharapkan dari algoritma paling baik adalah O (nlogn), ini adalah ketika jumlah titik paling jauh selalu pusat leksikografis. Namun, dalam kasus terburuk, kompleksitas algoritme adalah O (n ^ 2). Ini dicapai, misalnya, jika jumlah titik paling jauh selalu berdekatan dengan jumlah titik batas.
Saya harap artikel saya akan bermanfaat bagi seseorang, saya juga ingin menarik perhatian pada kenyataan bahwa jika artikel tersebut menunjukkan minat yang cukup di antara pembaca, saya akan segera siap untuk mempertimbangkan algoritma untuk menyederhanakan rantai poligonal Reumman-Witkam, Opheim dan Lang. Terima kasih atas perhatian anda!