
Pendahuluan
Artikel ini menjelaskan hasil percobaan yang dilakukan dalam rangka proyek "Nilai tukar absolut". Protokol eksperimental dapat dilihat dengan mengklik tautan .
Proyek “ Nilai tukar absolut ” terlibat dalam analisis nilai tukar berpasangan, alokasi nilai tukar absolut dari mereka dan analisisnya. Dalam kerangka kerja proyek, metodologi untuk mengkonversi dari nilai pasangan ke nilai tukar absolut diperoleh. Untuk ini, ABS mata uang absolut ditentukan. Semua mata uang yang tersedia dinyatakan dalam ABS.
Penjelasan rinci tentang teknologi diberikan dalam artikel " Dari pasangan mata uang hingga nilai tukar absolut ".
Hingga saat ini, beberapa artikel telah dipublikasikan tentang penerapan metode nilai tukar absolut. Saya membawa dua yang terakhir.
Artikel " Sebuah studi tentang keterkaitan mata uang dunia melalui korelasi tingkat absolut " menggambarkan salah satu aplikasi teknologi nilai tukar absolut. Metode formal untuk menghitung hubungan antara mata uang yang berbeda diberikan.
Artikel " Metode portofolio Markowitz sebagaimana diterapkan pada pasar valuta asing " menggambarkan teknologi yang sebelumnya tidak dapat diakses untuk mengoptimalkan portofolio mata uang asing.
Berikut ini menjelaskan metode konversi dari nilai tukar pasangan (relatif) ke absolut. Parameter numerik dari transformasi dan metodologi untuk perhitungannya diberikan.
Dalam file sumber, nilai tukar harian secara otomatis dimuat setiap hari dan yang absolut dihitung darinya.
Matriks transformasi diperoleh pada tahun 2017. Itu dihitung pada nilai tukar pasangan nyata dengan meminimalkan kesalahan penyimpangan dari nilai pasangan dipulihkan dari absolut. Sejak itu, tidak ada analisis kesalahan yang dilakukan pada data modern.
Hasil verifikasi tak terduga yang dijelaskan di bawah ini mengarah pada pengembangan teknik baru untuk mendapatkan matriks transformasi. Selain itu, kesalahan terdeteksi dalam memproses kutipan yang diimpor.
Alasan teoretis
Untuk mendapatkan nilai tukar absolut, Anda harus melakukan konversi berikut. Untuk memulai, kursus berpasangan adalah logaritma. Selanjutnya, kita mengalikannya dengan matriks transformasi terbalik. Pada akhirnya, kita kembali dari skala logaritmik menggunakan eksponen.
Untuk transisi lebih lanjut untuk memasangkan kursus, kursus absolut harus dicatat. Kemudian kalikan dengan matriks transformasi langsung. Kami menyimpulkan seperti sebelumnya menggunakan eksponen.
Teknologi ini dijelaskan secara lebih terperinci dalam artikel “ Dari pasangan mata uang hingga nilai absolut mata uang individual ” (hanya artikel ini pada tahun 2018 yang memberikan representasi transpose dari matriks transformasi yang berbeda dengan presentasi artikel ini).
Matriks langsung mudah ditentukan. Baris di dalamnya sesuai dengan mata uang, dan kolom terkait dengan pasangan mata uang. Matriksnya sangat jarang dan terdiri dari nol, satu, dan minus.
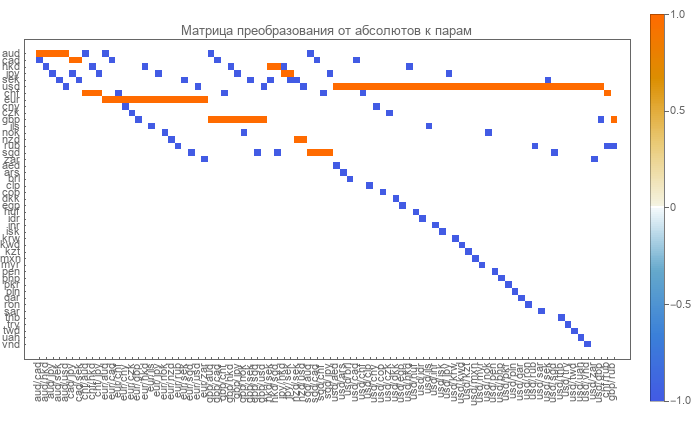
Nol menunjukkan tidak adanya pasangan dan mata uang tersebut. Unit terkait dengan mata uang dalam pembilang pasangan. Yang minus menunjukkan mata uang dalam penyebut pasangan.
Matriks transformasi terbalik dari pasangan ke tingkat absolut tidak ditentukan. Itu harus dihitung. Metode yang paling jelas adalah untuk meminimalkan kesalahan dalam pemulihan pasangan. Apa yang dilakukan untuk menghitung matriks ini pada tahun 2017. Kami memberikan representasi grafis dari matriks ini.
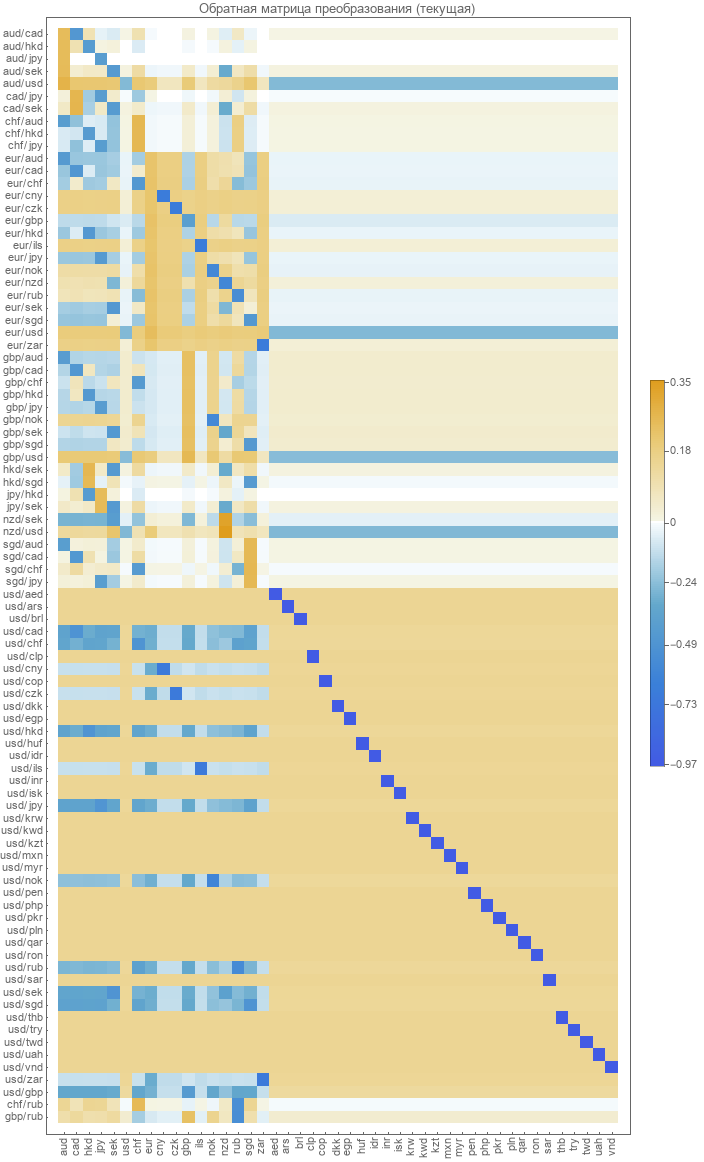
Memeriksa keakuratan model yang ada
Untuk matriks saat ini, nilai tukar pasangan absolut dan dipulihkan diperoleh. Ada perbedaan tajam antara kursus berpasangan asli dan dipulihkan.

Selanjutnya, perhitungan kesalahan pemulihan untuk semua pasangan dilakukan.
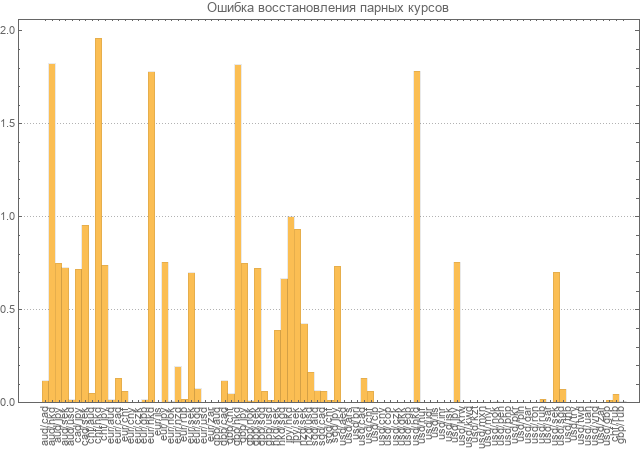
Kesalahan dianggap sebagai rata-rata penyimpangan relatif yang diambil modulo. Seperti dapat dilihat dalam diagram, kesalahan untuk banyak pasangan hampir dua kali lebih besar dari nilai itu sendiri.
Tentu saja, tingkat kesalahan ini tidak memungkinkan model dianggap konsisten dan membutuhkan penghitungan ulang.
Matriks terbalik semu dari sebuah garis
Hal pertama yang akan kita coba adalah menghitung matriks invers untuk matriks transformasi langsung. Karena fakta bahwa matriksnya non-square, kita harus menggunakan transformasi pseudo-invers . Hasilnya adalah sebagai berikut.
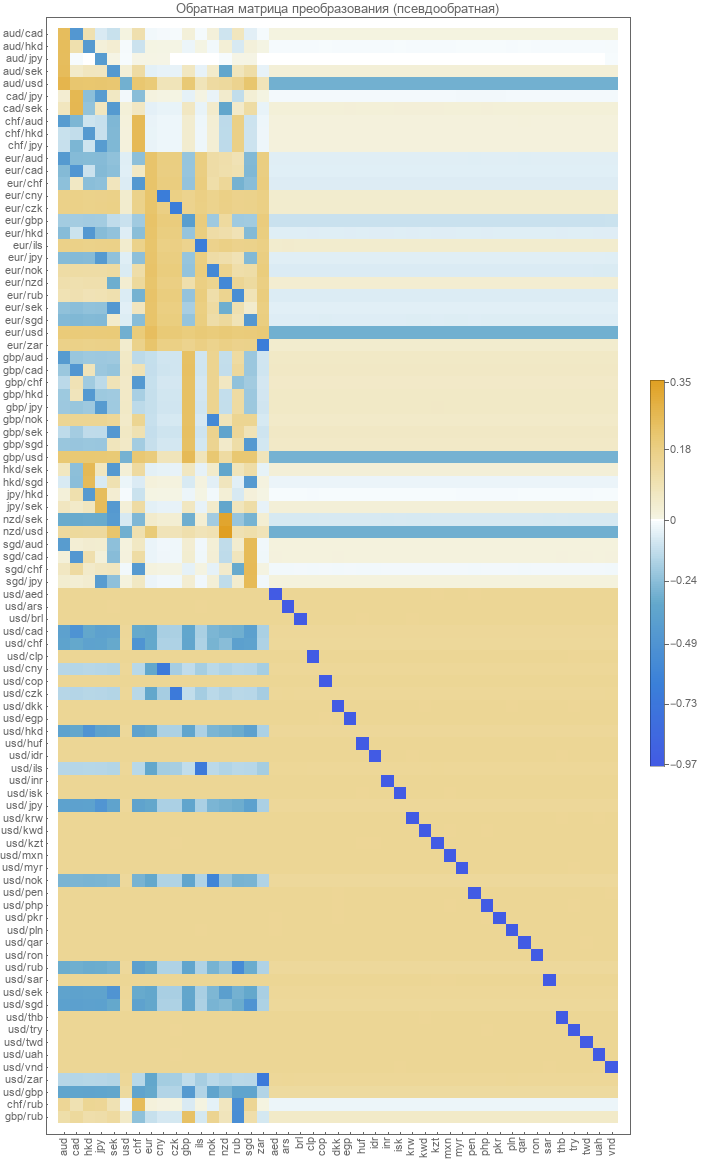
Ini sangat mirip dengan yang kami dapatkan sebelumnya menggunakan nilai tukar pasangan nyata untuk optimisasi.
Kami menghitung kursus absolut. Kemudian pulihkan dari kursus pasangan absolut. Bagan kesalahan adalah sebagai berikut.

Kesalahan juga ternyata besar, seperti dalam penilaian di atas. Model ini juga tidak cocok untuk kita.
Perhitungan matriks terbalik melalui komponen yang bebas linear
Jika kita menganalisis matriks transformasi langsung secara terperinci, kita dapat menemukan bahwa ia memiliki bentuk yang merosot ( pangkat matriks lebih kecil dari jumlah baris mata uang). Dengan kata lain, ada baris yang bergantung secara linear dalam matriks langsung. Dan karena itu, kita tidak bisa mendapatkan matriks terbalik yang dapat diterima.
Untuk keluar dari situasi ini, solusi berikut diusulkan. Dalam transisi dari kursus absolut ke berpasangan, Anda harus terlebih dahulu beralih ke komponen yang bebas linear. Dan baru kemudian beralih ke pasangan. Matriks transisi dari jalur absolut ke komponen dan dari komponen ke jalur berpasangan akan bersifat non-degenerasi dan matriks terbalik dapat diperoleh.
Untuk mencari komponen yang bebas linear, perlu untuk melampirkan matriks satuan dari kursus pasangan ke matriks transformasi langsung. Dengan demikian, kami memperoleh dua matriks transisi dari kursus absolut ke berpasangan dan matriks terlampir dari transisi dari berpasangan ke berpasangan.

Sekarang kita akan melakukan transformasi standar ke bentuk langkah dari bagian atas dari matriks gabungan ini (pada kenyataannya, alat standar dari paket matematika Wolfram Mathematica mengarah lebih jauh ke bentuk diagonal ). Akibatnya, dimungkinkan untuk mendapatkan matriks yang diubah berikut ini.

Sekarang di kolom matriks ini kita memiliki komponen yang bebas linear. Selain itu, kita dapat beralih ke keduanya dari mata kuliah absolut (bagian atas matriks) dan dari mata kuliah berpasangan (bagian bawah dari matriks transformasi gabungan).
Kami memilih matriks transisi ini untuk komponen yang bebas linear. Berikut ini adalah matriks transisi untuk komponen dari program absolut.
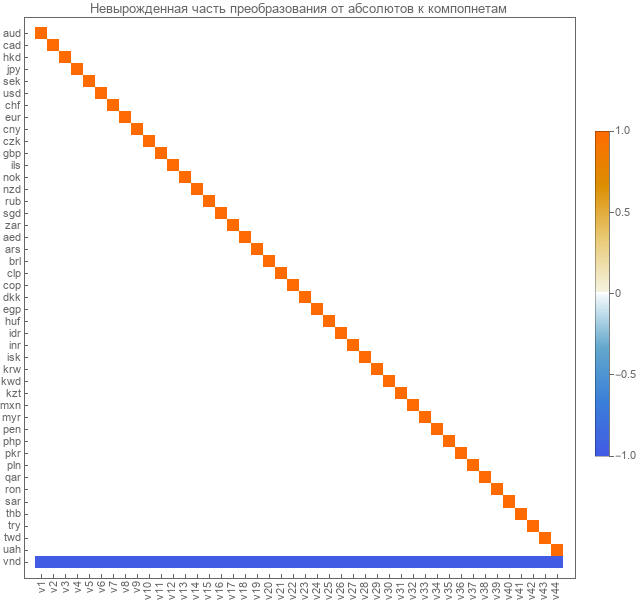
Berikut adalah matriks transisi dari kursus berpasangan ke komponen yang bebas linear.

Transisi dari absolut ke komponen terjadi melalui matriks yang dihitung di atas. Transformasi terbalik dari komponen ke absolut dilakukan melalui matriks terbalik. Karena fakta bahwa itu akan menjadi non-degenerasi, matriks invers yang baik dapat diperoleh. Kami akan menerima sebagai pseudo-invers. Inilah pandangannya.

Sekarang Anda bisa mendapatkan matriks transformasi terbalik lengkap dari pasangan ke absolut. Untuk melakukan ini, kita mengalikan matriks transformasi dari pasangan ke komponen dengan matriks transformasi terbalik dari komponen menjadi absolut. Dia terlihat seperti ini.

Meskipun kita sudah melihat yang serupa di atas, tetapi tetap saja matriksnya berbeda. Kami memeriksa hasil yang diberikannya. Kami akan menghitung kursus absolut, dan dari mereka kami akan mengembalikan dipasangkan. Kesalahan pemulihan adalah sebagai berikut.

Pada semua pasangan kecuali dua, hampir nol kesalahan. Kami mencari tahu apa yang salah dengan pasangan ini.
Ternyata dalam dua pasangan mata uang, data yang salah diterima. Untuk jpy / hkd dan jpy / sek, datanya sebanyak 10.000 dan 100 buah. Diperlukan untuk memperbaiki dan memeriksa ulang.
Setelah mengoreksi kursus pasangan input (menyingkirkan lot) dan menghitung ulang kursus pasangan absolut dan yang dipulihkan, kami melihat kesalahan pemulihan.

Mendapat kesalahan dalam 0,3%. Level kesalahan yang cukup bisa diterima.
Berikut ini adalah contoh dari grafik kursus absolut.
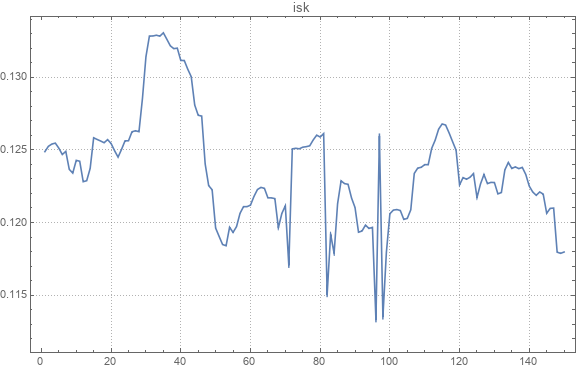
Berikut adalah contoh dari nilai tukar pasangan asli dan yang dipulihkan.

Karena kami telah menghitung ulang matriks baru dari transformasi terbalik, kami sekali lagi menyajikan data tentang tingkat absolut terbaru dari semua mata uang yang berpartisipasi.
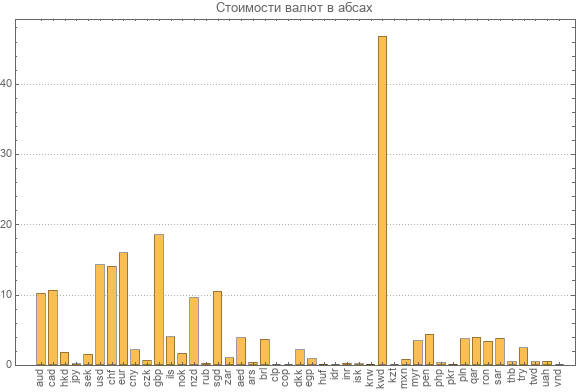
Anda dapat melihat mata uang paling mahal. Ini adalah dinar Kuwait senilai hampir 47 abs. Nilai absolut terkecil dari dong Vietnam adalah 0,003 abs.
Kesimpulan
Sebagai hasil dari penelitian, ditemukan bahwa metode yang ada untuk menghitung tingkat absolut memberikan kesalahan yang signifikan. Selain itu, kesalahan terdeteksi pada sumber data.
Kami berhasil mendapatkan matriks transformasi terbalik dari berpasangan menjadi absolut hanya menggunakan metode transformasi ke sejumlah kecil komponen yang bebas linear dengan matriks transformasi non-degenerasi.
Metode untuk mendapatkan matriks transformasi terbalik tidak menggunakan data tingkat pasangan. Dan karenanya tidak tergantung pada mereka.
Verifikasi konversi pada kursus nyata menunjukkan tingkat kesalahan yang rendah. Dari mana disimpulkan bahwa matriks yang ditemukan dari transformasi terbalik berlaku dari nilai tukar berpasangan menjadi absolut.
Metode ini tidak mengklaim telah dilengkapi dan diverifikasi secara matematis, tetapi sebagai solusi yang dapat diterima akan digunakan untuk studi lebih lanjut tentang nilai tukar absolutnya.