👩‍💻 🏂🏽 👐🏼 Optlib Implementasi algoritma optimasi genetik di Rust 🕋 👩🏿‍🔬 🐱

Artikel ini menjelaskan pustaka optlib , yang dirancang untuk memecahkan masalah optimisasi global dalam bahasa Rust. Pada saat penulisan ini, perpustakaan ini mengimplementasikan algoritma genetika untuk menemukan minimum fungsi global. Pustaka optlib tidak terikat pada tipe input spesifik untuk fungsi yang dioptimalkan. Juga, perpustakaan dibangun sedemikian rupa sehingga ketika menggunakan algoritma genetika, mudah untuk mengubah algoritma penyilangan, mutasi, seleksi, dan tahapan lain dari algoritma genetika. Bahkan, algoritma genetika disusun seolah-olah dari kubus.

Masalah optimasi global

Masalah optimasi biasanya dirumuskan sebagai berikut.

Untuk beberapa fungsi yang diberikan f ( x ), di antara semua nilai yang mungkin dari x, temukan nilai x 'sehingga f (x') mengambil nilai minimum (atau maksimum). Selain itu, x dapat menjadi bagian dari berbagai set - bilangan asli, bilangan real, bilangan kompleks, vektor atau matriks.

Maksud dari fungsi f ( x ) adalah titik x ' di mana turunan dari fungsi f ( x ) sama dengan nol.

Ada banyak algoritma yang dijamin untuk menemukan fungsi ekstrem, yang merupakan minimum lokal atau maksimum di dekat titik awal yang diberikan x ₀ . Algoritma semacam itu termasuk, misalnya, algoritma gradient descent. Namun, dalam praktiknya, seringkali perlu untuk menemukan minimum global (atau maksimum) dari suatu fungsi yang, dalam rentang x tertentu, selain satu ekstrem global, memiliki banyak ekstrem lokal.

Algoritma gradien tidak dapat mengatasi optimasi fungsi seperti itu, karena solusinya menyatu dengan ekstrem terdekat di dekat titik awal. Untuk masalah menemukan global maksimum atau minimum, apa yang disebut algoritma optimisasi global digunakan. Algoritma ini tidak menjamin menemukan ekstrem global, karena adalah algoritma probabilistik, tetapi tidak ada yang tersisa selain mencoba algoritma yang berbeda untuk tugas tertentu dan melihat algoritma mana yang akan lebih baik dalam mengatasi optimasi, lebih disukai dalam waktu sesingkat mungkin dan dengan probabilitas maksimum untuk menemukan ekstrem global.

Salah satu algoritma yang paling terkenal (dan sulit diimplementasikan) adalah algoritma genetika.

Skema umum dari algoritma genetika

Ide algoritma genetika lahir secara bertahap dan dibentuk pada akhir 1960-an - awal 1970-an. Algoritma genetika mendapat perkembangan yang kuat setelah rilis buku John Holland "Adaptation in Natural and Artificial Systems" (1975)

Algoritme genetik didasarkan pada pemodelan populasi individu selama sejumlah besar generasi. Dalam proses algoritma genetika, individu baru dengan parameter terbaik muncul, dan individu yang paling tidak sukses mati. Untuk kepastian, berikut ini adalah istilah yang digunakan dalam algoritma genetika.

Seorang individu adalah satu nilai x di antara sekumpulan nilai yang mungkin bersama dengan nilai fungsi objektif untuk suatu titik x .
Kromosom - nilai x .
Kromosom - nilai x _i jika x adalah vektor.
Fungsi kebugaran (fungsi kebugaran, fungsi tujuan) adalah fungsi yang dioptimalkan f ( x ).
Populasi adalah kumpulan individu.
Generasi - jumlah iterasi dari algoritma genetika.

Setiap individu mewakili satu nilai x di antara set semua solusi yang mungkin. Nilai fungsi yang dioptimalkan (di masa depan, untuk singkatnya, kami menganggap bahwa kami mencari fungsi minimum) dihitung untuk setiap nilai x . Kami berasumsi bahwa semakin tidak penting fungsi objektifnya, semakin baik solusi ini.

Algoritma genetika digunakan di banyak bidang. Sebagai contoh, mereka dapat digunakan untuk memilih bobot dalam jaringan saraf. Banyak sistem CAD menggunakan algoritma genetika untuk mengoptimalkan parameter perangkat untuk memenuhi persyaratan yang ditentukan. Algoritma optimisasi global juga dapat digunakan untuk memilih lokasi konduktor dan elemen di papan tulis.

Diagram struktural dari algoritma genetika ditunjukkan pada gambar berikut:

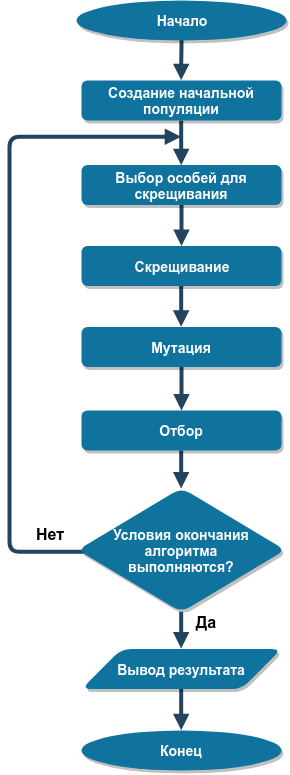
Kami mempertimbangkan setiap tahap algoritma secara lebih rinci.

Buat populasi awal

Tahap pertama dari algoritma adalah penciptaan populasi awal, yaitu, penciptaan banyak individu dengan nilai kromosom x yang berbeda . Sebagai aturan, populasi awal dibuat dari individu dengan nilai kromosom acak, sambil berusaha memastikan bahwa nilai-nilai kromosom dalam populasi mencakup seluruh area pencarian solusi yang relatif seragam, kecuali jika ada asumsi di mana ekstrem global dapat berada.

Alih-alih mendistribusikan kromosom secara acak, Anda dapat membuat kromosom sehingga nilai awal x terdistribusi secara merata di seluruh area pencarian dengan langkah tertentu, yang tergantung pada berapa banyak individu yang akan dibuat pada tahap algoritma ini.

Semakin banyak individu akan dibuat pada tahap ini, semakin besar kemungkinan algoritma akan menemukan solusi yang tepat, dan seiring dengan meningkatnya populasi awal, sebagai aturan, lebih sedikit iterasi dari algoritma genetika (jumlah generasi) yang diperlukan. Namun, dengan peningkatan ukuran populasi, peningkatan jumlah perhitungan fungsi objektif dan kinerja operasi genetik lainnya pada tahap selanjutnya dari algoritma diperlukan. Artinya, dengan peningkatan ukuran populasi, waktu perhitungan satu generasi meningkat.

Pada prinsipnya, ukuran populasi tidak harus tetap konstan di seluruh pekerjaan algoritma genetika, seringkali seiring dengan meningkatnya jumlah generasi, ukuran populasi dapat dikurangi, karena seiring waktu, semakin banyak individu akan berada lebih dekat ke solusi yang diinginkan. Namun, seringkali ukuran populasi dipertahankan kira-kira konstan.

Pemilihan individu untuk kawin silang

Setelah menciptakan populasi, perlu untuk menentukan individu mana yang akan berpartisipasi dalam operasi perkawinan silang (lihat paragraf berikutnya). Ada berbagai algoritma untuk tahap ini. Yang paling sederhana dari mereka adalah untuk menyeberang setiap individu dengan masing-masing, tetapi kemudian pada langkah selanjutnya Anda harus melakukan terlalu banyak operasi perkawinan silang dan menghitung nilai-nilai fungsi tujuan.

Lebih baik memberikan kesempatan yang lebih besar untuk mengawinkan individu dengan kromosom yang lebih berhasil (dengan nilai minimum dari fungsi tujuan), dan individu-individu yang fungsi obyektifnya lebih (lebih buruk) untuk menghilangkan kemampuan untuk meninggalkan keturunan.

Jadi, pada tahap ini, Anda perlu membuat pasangan individu (atau tidak harus berpasangan jika lebih banyak individu dapat berpartisipasi dalam persimpangan), untuk mana operasi persimpangan akan dilakukan pada tahap berikutnya.

Di sini Anda juga dapat menerapkan berbagai algoritma. Misalnya, buat pasangan secara acak. Atau Anda dapat mengurutkan individu dalam urutan naik dengan nilai fungsi objektif dan membuat pasangan individu yang berada lebih dekat ke awal daftar yang disortir (misalnya, dari individu di paruh pertama daftar, di sepertiga pertama daftar, dll.) Metode ini buruk karena membutuhkan waktu untuk memilah individu.

Metode turnamen sering digunakan. Ketika beberapa individu dipilih secara acak untuk peran masing-masing pelamar untuk persimpangan, di antaranya individu dengan nilai terbaik dari fungsi tujuan dikirim ke pasangan masa depan. Dan bahkan di sini orang dapat memperkenalkan unsur keacakan, memberikan peluang kecil bagi individu dengan nilai terburuk dari fungsi objektif untuk "mengalahkan" individu dengan nilai terbaik dari fungsi objektif. Ini memungkinkan Anda untuk mempertahankan populasi yang lebih heterogen, melindunginya dari degenerasi, yaitu dari situasi di mana semua individu memiliki nilai kromosom yang kira-kira sama, yang setara dengan menghentikan algoritma ke satu ekstrem, mungkin bukan global.

Hasil dari operasi ini akan menjadi daftar mitra untuk persimpangan.

Persilangan

Persilangan adalah operasi genetik yang menciptakan individu baru dengan nilai-nilai kromosom baru. Kromosom baru dibuat berdasarkan kromosom orang tua. Paling sering, dalam proses melintasi satu set pasangan, satu anak perempuan diciptakan, tetapi secara teoritis, lebih banyak anak dapat diciptakan.

Algoritma persimpangan juga dapat diimplementasikan dengan berbagai cara. Jika tipe kromosom adalah angka pada individu, maka hal paling sederhana yang dapat dilakukan adalah membuat kromosom baru sebagai rata-rata aritmatika atau rata-rata geometris dari kromosom orang tua. Untuk banyak tugas ini sudah cukup, tetapi paling sering digunakan algoritma lain berdasarkan operasi bit.

Persilangan bitwise bekerja sedemikian rupa sehingga kromosom anak perempuan terdiri dari bagian dari bit dari satu orang tua dan bagian dari bit dari orang tua yang lain, seperti yang ditunjukkan pada gambar berikut:

Titik pisah induk biasanya dipilih secara acak. Tidak perlu menciptakan dua anak dengan salib seperti itu, seringkali terbatas pada salah satunya.

Jika titik pemisahan kromosom induk adalah satu, maka persilangan seperti itu disebut titik tunggal. Tetapi Anda juga dapat menggunakan pemisahan multi-titik, ketika kromosom induk dibagi menjadi beberapa bagian, seperti yang ditunjukkan pada gambar berikut:

Dalam hal ini, lebih banyak kombinasi kromosom anak dimungkinkan.

Jika kromosom adalah angka titik mengambang, maka semua metode yang dijelaskan di atas dapat diterapkan padanya, tetapi mereka tidak akan sangat efektif. Sebagai contoh, jika angka floating-point disilangkan sedikit demi sedikit, seperti yang dijelaskan sebelumnya, maka banyak operasi penyeberangan akan membuat kromosom anak perempuan yang akan berbeda dari salah satu dari orang tua hanya di tempat desimal jauh. Situasi ini diperparah ketika menggunakan angka floating-point presisi ganda.

Untuk mengatasi masalah ini, perlu diingat bahwa angka floating point sesuai dengan standar IEEE 754 disimpan sebagai tiga angka integer: S (satu bit), M dan N, dari mana angka floating point dihitung sebagai x = (-1) ^S × M × 2 ^N. Salah satu cara melintasi angka titik-mengambang adalah dengan terlebih dahulu membagi angka menjadi komponen S, M, N, yang bilangan bulat, dan kemudian menerapkan operasi penyilangan bitwise yang dijelaskan di atas ke angka M dan N, pilih tanda S dari salah satu orang tua, dan dari nilai yang diperoleh membuat kromosom anak perempuan.

Dalam banyak masalah, seorang individu tidak memiliki satu, tetapi beberapa kromosom, dan bahkan dapat dari berbagai jenis (bilangan bulat dan angka floating-point). Lalu ada lebih banyak pilihan untuk melintasi kromosom tersebut. Misalnya, saat membuat anak perempuan, Anda dapat melewati semua kromosom orang tua, atau Anda dapat mentransfer beberapa kromosom dari salah satu orang tua tanpa perubahan.

Mutasi

Mutasi adalah tahap penting dari algoritma genetika yang mendukung keragaman kromosom individu dan dengan demikian mengurangi kemungkinan bahwa solusi akan dengan cepat menyatu ke beberapa minimum lokal daripada global. Mutasi adalah perubahan acak dalam kromosom individu yang baru saja dibuat dengan menyeberang.

Sebagai aturan, probabilitas mutasi tidak diatur sangat tinggi sehingga mutasi tidak mengganggu konvergensi algoritma, jika tidak maka akan merusak individu dengan kromosom yang sukses.

Seperti halnya untuk persimpangan, algoritma yang berbeda dapat digunakan untuk mutasi. Misalnya, Anda dapat mengganti satu kromosom atau beberapa kromosom dengan nilai acak. Tetapi paling sering, mutasi bitwise digunakan ketika satu bit atau beberapa bit terbalik dalam kromosom (atau dalam beberapa kromosom), seperti yang ditunjukkan pada gambar berikut.

Mutasi satu bit:

Mutasi beberapa bit:

Jumlah bit untuk mutasi dapat ditentukan sebelumnya atau menjadi variabel acak.

Sebagai hasil dari mutasi, individu dapat menjadi lebih sukses dan kurang berhasil, tetapi operasi ini memungkinkan kromosom yang sukses dengan set nol dan yang orang tua tidak harus muncul dengan probabilitas nol.

Seleksi

Sebagai hasil dari persilangan dan mutasi selanjutnya, individu baru muncul. Jika tidak ada tahap seleksi, jumlah individu akan tumbuh secara eksponensial, yang akan membutuhkan lebih banyak RAM dan waktu pemrosesan untuk setiap generasi populasi yang baru. Oleh karena itu, setelah munculnya individu baru, perlu untuk membersihkan populasi individu yang paling tidak berhasil. Inilah yang terjadi pada tahap seleksi.

Algoritma seleksi juga bisa berbeda. Seringkali, individu yang kromosomnya tidak jatuh dalam interval tertentu dari pencarian solusi pertama kali dibuang.

Anda kemudian dapat menurunkan sebanyak mungkin individu yang paling tidak berhasil untuk mempertahankan ukuran populasi yang konstan. Berbagai kriteria probabilistik untuk seleksi juga dapat diterapkan, misalnya, probabilitas pemilihan individu dapat bergantung pada nilai fungsi tujuan.

Kondisi Akhir Algoritma

Seperti pada tahap lain dari algoritma genetika, ada beberapa kriteria untuk mengakhiri algoritma.

Kriteria paling sederhana untuk mengakhiri suatu algoritma adalah untuk membatalkan algoritma setelah nomor iterasi (generasi) yang diberikan. Tetapi kriteria ini harus digunakan dengan hati-hati, karena algoritma genetika adalah probabilistik, dan awal yang berbeda dari algoritma dapat bertemu pada kecepatan yang berbeda. Biasanya, kriteria terminasi oleh nomor iterasi digunakan sebagai kriteria tambahan jika algoritma gagal menemukan solusi selama sejumlah besar iterasi. Oleh karena itu, angka yang cukup besar harus ditetapkan sebagai ambang angka iterasi.

Kriteria berhenti lain adalah bahwa algoritma terganggu jika solusi terbaik baru tidak muncul untuk sejumlah iterasi tertentu. Ini berarti bahwa algoritme telah menemukan ekstrem global atau terjebak dalam ekstrem lokal.

Ada juga situasi yang tidak menguntungkan ketika kromosom semua individu memiliki arti yang sama. Inilah yang disebut populasi yang merosot. Kemungkinan besar dalam hal ini, algoritma terjebak dalam satu ekstrim, dan belum tentu global. Hanya mutasi yang berhasil yang dapat mengeluarkan populasi dari keadaan ini, tetapi karena probabilitas mutasi biasanya dibuat kecil, dan itu jauh dari kenyataan bahwa mutasi akan menciptakan individu yang lebih sukses, situasi dengan populasi yang merosot biasanya dianggap sebagai alasan untuk menghentikan algoritma genetika. Untuk memeriksa kriteria ini, perlu membandingkan kromosom semua individu, apakah ada perbedaan di antara mereka, dan jika tidak ada perbedaan, maka hentikan algoritma.

Dalam beberapa masalah, tidak perlu menemukan minimum global, melainkan menemukan solusi yang baik - solusi yang nilai fungsinya kurang dari nilai yang diberikan. Dalam hal ini, algoritma dapat dihentikan terlebih dahulu jika solusi yang ditemukan pada iterasi berikutnya memenuhi kriteria ini.

optlib

Optlib adalah perpustakaan untuk bahasa Rust, yang dirancang untuk mengoptimalkan fungsi. Pada saat menulis baris-baris ini, hanya algoritma genetika yang diterapkan di perpustakaan, tetapi di masa depan direncanakan untuk memperluas perpustakaan ini dengan menambahkan algoritma optimasi baru ke dalamnya. Optlib sepenuhnya ditulis dalam Rust.

Optlib adalah perpustakaan open source yang didistribusikan di bawah lisensi MIT.

Halaman di github - https://github.com/Jenyay/rust-optimization
Halaman di crates.io - https://crates.io/crates/optlib
Dokumentasi - https://docs.rs/optlib

optlib :: genetik

Dari deskripsi algoritma genetika, dapat dilihat bahwa banyak tahapan algoritma dapat diimplementasikan dengan cara yang berbeda, memilihnya sehingga untuk fungsi objektif yang diberikan, algoritma tersebut menyatu ke solusi yang tepat dalam jumlah waktu minimum.

Modul optlib :: genetic dirancang sedemikian rupa sehingga memungkinkan untuk merakit algoritma genetika “dari kubus”. Saat membuat instance dari struktur di mana pekerjaan algoritma genetika akan terjadi, Anda perlu menentukan algoritma mana yang akan digunakan untuk membuat populasi, memilih mitra, memotong, bermutasi, memilih, dan kriteria apa yang digunakan untuk menghentikan algoritma.

Perpustakaan sudah memiliki algoritma yang paling sering digunakan untuk tahapan algoritma genetika, tetapi Anda bisa membuat tipe Anda sendiri yang mengimplementasikan algoritma yang sesuai.

Di perpustakaan, kasus di mana kromosom adalah vektor bilangan pecahan, yaitu ketika fungsi f ( x ) diminimalkan, di mana x adalah vektor angka floating-point ( f32 atau f64 ).

Contoh optimasi menggunakan optlib :: genetic

Sebelum kita mulai menjelaskan modul genetik secara terperinci, pertimbangkan sebuah contoh penggunaannya untuk meminimalkan fungsi Schwefel. Fungsi multidimensi ini dihitung sebagai berikut:

F (b o l d s y m b o l x) = 418.9829 N - s u m_{i = 1}^{N} x_{i} s i n (s q r t | x_{i} |)

$F (\ boldsymbol x) = 418.9829N - \ sum_ {i = 1} ^ {N} x_i \ sin (\ sqrt {| x_i |})$

Fungsi Schweffel minimum dalam interval -500 <= x _i <= 500 terletak di titik x ' , di mana semua x _i = 420.9687 untuk i = 1, 2, ..., N, dan nilai fungsi pada titik ini adalah f ( x' ) = 0.

Jika N = 2, maka gambar tiga dimensi dari fungsi ini adalah sebagai berikut:

Ekstrem lebih jelas terlihat jika kita membangun garis level fungsi ini:

Contoh berikut menunjukkan bagaimana menggunakan modul genetik untuk menemukan fungsi Schweffel minimum. Anda dapat menemukan contoh ini dalam kode sumber di folder contoh / genetik-schwefel.

//!    . //! //! y = f(x),  x = (x0, x1, ..., xi,... xn). //!      x' = (420.9687, 420.9687, ...) //!      xi - [-500.0; 500.0]. //! f(x') = 0 //! //! #  //! * ` ` -   . y = f(x). //! * `` -    , x = (x0, x1, x2, ..., xn). //! * `` -   x    . //! * `` -  . //! * `` -    . use optlib::genetic; use optlib::genetic::creation; use optlib::genetic::cross; use optlib::genetic::goal; use optlib::genetic::logging; use optlib::genetic::mutation; use optlib::genetic::pairing; use optlib::genetic::pre_birth; use optlib::genetic::selection; use optlib::genetic::stopchecker; use optlib::testfunctions; use optlib::Optimizer; ///    type Gene = f32; ///   type Chromosomes = Vec<Gene>; fn main() { //   //  .  xi     [-500.0; 500.0] let minval: Gene = -500.0; let maxval: Gene = 500.0; //      let population_size = 500; //   xi  . //  15-   let chromo_count = 15; let intervals = vec![(minval, maxval); chromo_count]; //      ( ) //      optlib::testfunctions let goal = goal::GoalFromFunction::new(testfunctions::schwefel); //       . // RandomCreator       . let creator = creation::vec_float::RandomCreator::new(population_size, intervals.clone()); //        //     . let partners_count = 2; let families_count = population_size / 2; let rounds_count = 5; let pairing = pairing::Tournament::new(partners_count, families_count, rounds_count); //   //      , //   -     let single_cross = cross::FloatCrossExp::new(); let cross = cross::VecCrossAllGenes::new(Box::new(single_cross)); //    //    (     ). let mutation_probability = 15.0; let mutation_gene_count = 3; let single_mutation = mutation::BitwiseMutation::new(mutation_gene_count); let mutation = mutation::VecMutation::new(mutation_probability, Box::new(single_mutation)); // .       , //     . let pre_births: Vec<Box<genetic::PreBirth<Chromosomes>>> = vec![Box::new( pre_birth::vec_float::CheckChromoInterval::new(intervals.clone()), )]; //    //   ,       1e-4 //   3000  (). let stop_checker = stopchecker::CompositeAny::new(vec![ Box::new(stopchecker::Threshold::new(1e-4)), Box::new(stopchecker::MaxIterations::new(3000)), ]); //    .  -   . //        NaN  Inf. //    ,     . let selections: Vec<Box<dyn genetic::Selection<Chromosomes>>> = vec![ Box::new(selection::KillFitnessNaN::new()), Box::new(selection::LimitPopulation::new(population_size)), ]; //     . //       , //       . let loggers: Vec<Box<genetic::Logger<Chromosomes>>> = vec![ Box::new(logging::StdoutResultOnlyLogger::new(15)), Box::new(logging::TimeStdoutLogger::new()), ]; //     let mut optimizer = genetic::GeneticOptimizer::new( Box::new(goal), Box::new(stop_checker), Box::new(creator), Box::new(pairing), Box::new(cross), Box::new(mutation), selections, pre_births, loggers, ); //    optimizer.find_min(); }

Contoh ini dapat dijalankan dari root sumber dengan menjalankan perintah

 cargo run --bin genetic-schwefel --release

Hasilnya akan terlihat seperti ini:

 Solution: 420.962615966796875 420.940093994140625 420.995391845703125 420.968505859375000 420.950866699218750 421.003784179687500 421.001281738281250 421.300537109375000 421.001708984375000 421.012603759765625 420.880493164062500 420.925079345703125 420.967559814453125 420.999237060546875 421.011505126953125 Goal: 0.015625000000000 Iterations count: 3000 Time elapsed: 2617 ms

Sebagian besar kode sampel terlibat dalam pembuatan objek sifat untuk berbagai tahap algoritma genetika. Seperti yang ditulis di awal artikel, setiap tahapan algoritma genetika dapat diimplementasikan dengan berbagai cara. Untuk menggunakan modul optlib :: genetic, Anda perlu membuat objek sifat yang mengimplementasikan setiap langkah dengan satu atau lain cara. Kemudian semua objek ini dipindahkan ke konstruktor dari struktur GeneticOptimizer, di mana algoritma genetika diimplementasikan.

Metode find_min () dari struktur GeneticOptimizer memulai eksekusi algoritma genetika.

Jenis dan objek dasar

Ciri-ciri dasar modul optlib

Pustaka optlib dikembangkan dengan tujuan bahwa algoritma pengoptimalan baru akan ditambahkan di masa mendatang sehingga program dapat dengan mudah beralih dari satu algoritma pengoptimalan ke yang lain, oleh karena itu modul optlib berisi sifat Pengoptimal , yang mencakup satu metode - find_min (), yang menjalankan algoritma pengoptimalan saat eksekusi. Di sini tipe T adalah tipe objek, yang merupakan titik dalam ruang pencarian solusi. Misalnya, dalam contoh di atas, ini adalah Vec <Gene> (di mana Gene adalah alias untuk f32). Artinya, ini adalah tipe yang objeknya diumpankan ke input fungsi objektif.

Sifat Pengoptimal dinyatakan dalam modul optlib sebagai berikut:

 pub trait Optimizer<T> { fn find_min(&mut self) -> Option<(&T, f64)>; }

Metode find_min () optim_ trait harus mengembalikan objek bertipe Option <(& T, f64)>, di mana & T dalam tuple yang dikembalikan adalah solusi yang ditemukan, dan f64 adalah nilai fungsi tujuan untuk solusi yang ditemukan. Jika algoritme tidak dapat menemukan solusi, maka fungsi find_min () harus mengembalikan Tidak Ada.

Karena banyak algoritma optimisasi stokastik menggunakan apa yang disebut agen (dalam hal algoritma genetika, agen adalah individu), modul optlib juga berisi sifat AlgorithmWithAgents dengan metode get_agents () tunggal yang harus mengembalikan vektor agen.

Agen, pada gilirannya, adalah struktur yang mengimplementasikan sifat lain dari optlib - Agen .

Karakter AlgorithmWithAgents dan Agent dinyatakan dalam modul optlib sebagai berikut:

 pub trait AlgorithmWithAgents<T> { type Agent: Agent<T>; fn get_agents(&self) -> Vec<&Self::Agent>; } pub trait Agent<T> { fn get_parameter(&self) -> &T; fn get_goal(&self) -> f64; }

Untuk AlgorithmGithAgents dan Agent, tipe T memiliki arti yang sama dengan Pengoptimal, yaitu jenis objek yang nilai fungsinya dihitung.

Struktur GeneticOptimizer - Implementasi Algoritma Genetika

Kedua jenis diimplementasikan untuk struktur GeneticOptimizer - Optimizer dan AlgorithmWithAgents.

Setiap tahap dari algoritma genetika diwakili oleh tipenya sendiri, yang dapat diimplementasikan dari awal atau menggunakan salah satu dari implementasi optlib :: genetic yang tersedia di dalamnya. Untuk setiap tahap dari algoritma genetika, di dalam modul optlib :: genetik terdapat submodule dengan struktur tambahan dan fungsi yang mengimplementasikan algoritma yang paling sering digunakan dari tahapan algoritma genetika. Tentang modul-modul ini akan dibahas di bawah ini. Juga di dalam beberapa submodul ini terdapat submodul vec_float yang mengimplementasikan langkah-langkah algoritma untuk kasus ketika fungsi objektif dihitung dari vektor angka floating-point (f32 atau f64).

Konstruktor struktur GeneticOptimizer dinyatakan sebagai berikut:

 impl<T: Clone> GeneticOptimizer<T> { pub fn new( goal: Box<dyn Goal<T>>, stop_checker: Box<dyn StopChecker<T>>, creator: Box<dyn Creator<T>>, pairing: Box<dyn Pairing<T>>, cross: Box<dyn Cross<T>>, mutation: Box<dyn Mutation<T>>, selections: Vec<Box<dyn Selection<T>>>, pre_births: Vec<Box<dyn PreBirth<T>>>, loggers: Vec<Box<dyn Logger<T>>>, ) -> GeneticOptimizer<T> { ... } ... }

Konstruktor GeneticOptimizer menerima banyak jenis objek yang memengaruhi setiap tahap algoritma genetika, serta output dari hasilnya:

goal: Box <dyn Goal <T>> - fungsi objektif;
stop_checker: Box <dyn StopChecker <T>> - stop kriteria;
creator: Box <dyn Creator <T>> - buat populasi awal;
pairing: Box <dyn Pairing <T>> - algoritma untuk memilih mitra yang akan dilintasi;
cross: Box <dyn Cross <T>> - algoritma penyilangan;
mutasi: Box <dyn Mutation <T>> - algoritma mutasi;
Pilihan: Vec <Box <dyn Selection <T> >> - vektor algoritma seleksi;
pre_births: Vec <Box <dyn PreBirth <T> >> - vektor algoritma untuk menghancurkan kromosom yang gagal sebelum membuat individu;
loggers: Vec <Box <dyn Logger <T> >> - vektor objek yang mempertahankan log dari algoritma genetika.

Untuk menjalankan algoritme, Anda harus menjalankan metode find_min () dari sifat Pengoptimal. Selain itu, struktur GeneticOptimizer memiliki metode next_iterations (), yang dapat digunakan untuk melanjutkan perhitungan setelah metode find_min () selesai.

Terkadang setelah menghentikan algoritme, ada baiknya mengubah parameter algoritme atau metode yang digunakan. Ini dapat dilakukan dengan menggunakan metode struktur GeneticOptimizer berikut: replace_pairing (), replace_cross (), replace_mutation (), replace_pre_birth (), replace_selection (), replace_stop_checker (). Metode ini memungkinkan Anda untuk mengganti objek sifat yang diteruskan ke struktur GeneticOptimizer ketika dibuat.

Jenis utama untuk algoritma genetika dibahas pada bagian berikut.

Sasaran sifat - fungsi tujuan

Ciri Goal dinyatakan dalam modul optlib :: genetik sebagai berikut:

 pub trait Goal<T> { fn get(&self, chromosomes: &T) -> f64; }

Metode get () harus mengembalikan nilai fungsi objektif untuk kromosom yang diberikan.

Di dalam modul optlib :: genetic :: goal , ada struktur GoalFromFunction yang mengimplementasikan sifat Goal. Untuk struktur ini, ada konstruktor yang mengambil fungsi, yaitu fungsi target. Artinya, menggunakan struktur ini, Anda bisa membuat objek tipe Goal dari fungsi biasa.

Sifat pencipta - menciptakan populasi awal

Sifat Pencipta menggambarkan "pencipta" populasi awal. Sifat ini dinyatakan sebagai berikut:

 pub trait Creator<T: Clone> { fn create(&mut self) -> Vec<T>; }

Metode create () harus mengembalikan vektor kromosom berdasarkan populasi awal yang akan dibuat.

Untuk kasus di mana fungsi beberapa angka floating-point dioptimalkan, modul optlib :: genetic :: creator :: vec_float memiliki struktur RandomCreator <G> untuk membuat distribusi awal kromosom secara acak.

Selanjutnya, tipe <G> adalah tipe satu kromosom dalam vektor kromosom (kadang-kadang istilah "gen" digunakan alih-alih istilah "kromosom"). Pada dasarnya, tipe <G> akan berarti tipe f32 atau f64 jika kromosomnya adalah tipe Vec <f32> atau Vec <f64>.

Struktur RandomCreator <G> dinyatakan sebagai berikut:

 pub struct RandomCreator<G: Clone + NumCast + PartialOrd> { ... }

Di sini NumCast adalah jenis dari num crate. Tipe ini memungkinkan Anda untuk membuat tipe dari tipe numerik lain menggunakan metode from ().

Untuk membuat struktur RandomCreator <G>, Anda harus menggunakan fungsi baru (), yang dinyatakan sebagai berikut:

 pub fn new(population_size: usize, intervals: Vec<(G, G)>) -> RandomCreator<G> { ... }

Di sini, populasi_ukuran adalah ukuran populasi (jumlah set kromosom yang akan dibuat), dan interval adalah vektor tupel dari dua elemen - nilai minimum dan maksimum dari kromosom (gen) yang sesuai dalam set kromosom, dan ukuran vektor ini menentukan berapa banyak kromosom yang terkandung dalam set kromosom. masing-masing individu.

Pada contoh di atas, fungsi Schweffel dioptimalkan untuk 15 variabel tipe f32. Setiap variabel harus berada dalam kisaran [-500; 500]. Artinya, untuk membuat populasi, vektor interval harus berisi 15 tupel (-500.0f32, 500.0f32).

Jenis Pasangan - pemilihan mitra untuk persimpangan

Sifat Pairing digunakan untuk memilih individu yang akan kawin. Sifat ini dinyatakan sebagai berikut:

 pub trait Pairing<T: Clone> { fn get_pairs(&mut self, population: &Population<T>) -> Vec<Vec<usize>>; }

Metode get_pairs () mengambil pointer ke struktur Populasi , yang berisi semua individu dalam populasi, dan juga melalui struktur ini Anda bisa mengetahui individu-individu terbaik dan terburuk dalam populasi.

Metode get_pairs () pasangan harus mengembalikan vektor yang berisi vektor yang menyimpan indeks individu yang akan kawin campur. Bergantung pada algoritma penyilangan (yang akan dibahas pada bagian selanjutnya), dua atau lebih individu dapat menyeberang.

Misalnya, jika individu dengan indeks 0 dan 10, 5 dan 2, 6 dan 3 dilintasi, metode get_pairs () harus mengembalikan vektor vektor! [Vec! [0, 10], vec! [5, 2], vec! [ 6, 3]].

Modul optlib :: genetic :: pairing berisi dua struktur yang mengimplementasikan berbagai algoritma pemilihan mitra.

Untuk struktur RandomPairing , tipe Pairing diimplementasikan sedemikian rupa sehingga mitra dipilih secara acak untuk persimpangan.

Untuk struktur Turnamen , sifat Pairing diimplementasikan sedemikian rupa sehingga metode turnamen digunakan. Metode turnamen menyiratkan bahwa setiap individu yang akan berpartisipasi dalam salib harus mengalahkan individu lain (nilai fungsi objektif individu yang menang harus lebih kecil). Jika metode turnamen menggunakan satu putaran, ini berarti bahwa dua individu dipilih secara acak, dan seorang individu dengan nilai fungsi obyektif yang lebih rendah di antara dua individu ini masuk ke "keluarga" di masa depan. Jika beberapa putaran digunakan, maka individu yang menang dengan cara ini harus menang melawan beberapa individu secara acak.

Konstruktor struktur turnamen dinyatakan sebagai berikut:

 pub fn new(partners_count: usize, families_count: usize, rounds_count: usize) -> Tournament { ... }

Di sini:

partners_count - jumlah individu yang diperlukan untuk persimpangan;
Families_count - jumlah "keluarga", yaitu set individu yang akan menghasilkan keturunan;
rounds_count - jumlah putaran di turnamen.

Sebagai modifikasi lebih lanjut dari metode turnamen, Anda dapat menggunakan generator angka acak untuk memberikan peluang kecil untuk mengalahkan individu dengan nilai terburuk dari fungsi tujuan, yaitu untuk membuat probabilitas kemenangan dipengaruhi oleh nilai fungsi objektif, dan semakin besar perbedaan antara dua pesaing, semakin besar peluang untuk memenangkan individu terbaik, dan dengan nilai fungsi objektif yang hampir sama, probabilitas kemenangan satu individu akan mendekati 50%.

Jenis Cross - Crossing

Setelah "keluarga" individu terbentuk, untuk menyeberang, Anda perlu menyilangkan kromosom mereka untuk mendapatkan anak-anak dengan kromosom baru. Tahap persimpangan diwakili oleh tipe Cross , yang dinyatakan sebagai berikut:

 pub trait Cross<T: Clone> { fn cross(&mut self, parents: &[&T]) -> Vec<T>; }

Metode cross () melintasi satu set orang tua. Metode ini menerima parameter orang tua - sepotong dari referensi kromosom orang tua (bukan individu itu sendiri) - dan harus mengembalikan vektor dari kromosom baru. Ukuran orang tua tergantung pada algoritme untuk memilih mitra untuk persimpangan menggunakan sifat Pairing , yang dijelaskan pada bagian sebelumnya. Sering digunakan suatu algoritma yang menciptakan kromosom baru berdasarkan pada kromosom dari dua orang tua, maka ukuran orang tua akan sama dengan dua.

Modul optlib :: genetic :: cross berisi struktur yang tipe Cross diimplementasikan dengan algoritma penyilangan yang berbeda.

VecCrossAllGenes - struktur yang dirancang untuk melintasi kromosom, ketika masing-masing individu memiliki satu set kromosom - ini adalah vektor. Konstruktor VecCrossAllGenes menerima tipe objek Silang yang akan diterapkan ke semua elemen vektor kromosom induk. Dalam hal ini, ukuran vektor kromosom induk harus berukuran sama. Contoh di atas menggunakan struktur VecCrossAllGenes karena kromosom pada individu yang digunakan adalah tipe Vec <f32>.
CrossMean adalah struktur yang memotong dua angka sedemikian rupa sehingga sebagai kromosom anak akan ada angka yang dihitung sebagai rata-rata aritmatika dari kromosom induk.
FloatCrossGeometricMean adalah struktur yang memotong dua angka sedemikian rupa sehingga sebagai kromosom anak akan ada angka yang dihitung sebagai rata-rata geometris dari kromosom induk. Harus ada angka titik apung sebagai kromosom.
CrossBitwise - persilangan satu titik bitwise dari dua angka.
FloatCrossExp - persimpangan titik bitwise tunggal dari angka floating point. Mantissa dan peserta pameran orangtua secara independen menyeberang. Anak menerima tanda dari salah satu orang tua.

Modul optlib :: genetic :: cross juga berisi fungsi untuk nomor crossing bitwise dari berbagai tipe - integer dan floating point.

Jenis Mutasi - Mutasi

Setelah menyeberang, perlu untuk bermutasi anak-anak yang diperoleh untuk menjaga keragaman kromosom, dan populasi tidak meluncur ke keadaan merosot. Untuk populasi, Mutasi sifat dimaksudkan, yang dinyatakan sebagai berikut:

 pub trait Mutation<T: Clone> { fn mutation(&mut self, chromosomes: &T) -> T; }

Satu-satunya metode mutasi () dari sifat Mutasi mengambil referensi ke kromosom dan harus mengembalikan kemungkinan kromosom diubah. Sebagai aturan, probabilitas kecil dari mutasi ditetapkan, misalnya, beberapa persen, sehingga kromosom yang diperoleh atas dasar orang tua tetap ada, dan dengan demikian meningkatkan populasi.

Beberapa algoritma mutasi sudah diterapkan dalam modul optlib :: genetic :: mutation .

Modul ini, misalnya, berisi struktur VecMutation , yang bekerja mirip dengan struktur VecCrossAllGenes , yaitu jika kromosom adalah vektor, VecMutation menerima jenis objek Mutasi dan menerapkannya dengan probabilitas yang diberikan untuk semua elemen vektor, menciptakan vektor baru dengan gen bermutasi (elemen dari vektor kromosom).

Modul optlib :: genetic :: mutation juga berisi struktur BitwiseMutation yang menerapkan sifat Mutasi. Struktur ini membalikkan sejumlah bit acak dalam kromosom yang dikirimkan ke sana. Dianjurkan untuk menggunakan struktur ini bersama dengan struktur VecMutation.

Ciri PreBirth - pra-seleksi

Setelah menyeberang dan bermutasi, tahap seleksi biasanya terjadi, di mana individu yang paling tidak berhasil dihancurkan. Namun, dalam penerapan algoritma genetika di perpustakaan optlib :: genetik, sebelum langkah seleksi, ada langkah lain di mana kromosom yang tidak berhasil dapat dibuang. Langkah ini ditambahkan karena perhitungan fungsi objektif untuk individu sering membutuhkan banyak waktu, dan tidak perlu menghitungnya jika kromosom tidak jatuh ke dalam interval pencarian yang diketahui. Misalnya, dalam contoh di atas, kromosom yang tidak jatuh pada segmen [-500; 500].

Untuk melakukan pra-penyaringan seperti itu, sifat PreBirth dimaksudkan , yang dinyatakan sebagai berikut:

 pub trait PreBirth<T: Clone> { fn pre_birth(&mut self, population: &Population<T>, new_chromosomes: &mut Vec<T>); }

Satu-satunya metode preBirth () dari sifat PreBirth adalah referensi ke struktur Populasi yang disebutkan di atas, serta referensi yang bisa berubah ke vektor kromosom new_chromosomes. Ini adalah vektor kromosom yang diperoleh setelah langkah mutasi. Implementasi metode pre_birth () harus menghapus kromosom-kromosom tersebut dari vektor ini yang jelas-jelas tidak cocok untuk kondisi masalah.

Untuk kasus di mana fungsi vektor angka floating-point dioptimalkan, modul optlib :: genetic :: pre_birth :: vec_float berisi struktur CheckChromoInterval , yang dirancang untuk menghapus kromosom jika mereka adalah vektor angka floating-point, dan beberapa elemen vektor tidak termasuk dalam interval yang ditentukan.

Konstruktor untuk struktur CheckChromoInterval adalah sebagai berikut:

 pub fn new(intervals: Vec<(G, G)>) -> CheckChromoInterval<G> { ... }

Di sini, konstruktor mengambil vektor tupel dengan dua elemen - nilai minimum dan maksimum untuk setiap elemen dalam kromosom. Dengan demikian, ukuran vektor interval harus sesuai dengan ukuran vektor kromosom individu. Dalam contoh di atas, vektor 15 tupel (-500.0f32, 500.0f32) digunakan sebagai interval.

Seleksi Seleksi - Seleksi

Setelah seleksi awal kromosom, individu dibuat dan ditempatkan dalam populasi (struktur populasi ). Dalam proses menciptakan individu untuk masing-masing dari mereka, nilai fungsi objektif dihitung. Pada tahap seleksi, perlu untuk menghancurkan sejumlah individu sehingga populasi tidak tumbuh tanpa batas. Untuk ini, sifat Seleksi digunakan, yang dinyatakan sebagai berikut:

 pub trait Selection<T: Clone> { fn kill(&mut self, population: &mut Population<T>); }

Objek yang mengimplementasikan sifat Seleksi dalam metode kill () harus memanggil metode kill () dari struktur Individual (individu) untuk setiap individu dalam populasi yang perlu dihancurkan.

Untuk mem-bypass semua individu dalam suatu populasi, Anda bisa menggunakan iterator yang mengembalikan metode IterMut () dari struktur Population.

Karena sering diperlukan untuk menerapkan beberapa kriteria seleksi, ketika membuat struktur GeneticOptimizer , konstruktor menerima vektor objek tipe Seleksi.

Seperti halnya tahapan lain dari algoritma genetika, modul optlib :: genetic :: selection sudah menawarkan beberapa implementasi tahap seleksi.

KillFitnessNaN - menghancurkan individu di mana nilai fungsi objektif adalah NaN atau Inf.
LimitPopulation - menghancurkan sejumlah individu terburuk sehingga ukuran populasi tidak melebihi ukuran yang diberikan.
optlib :: genetic :: selection :: vec_float :: CheckChromoInterval - seandainya fungsi vektor angka floating-point dioptimalkan, ia menghancurkan individu yang nilai kromosomnya tidak sesuai dengan interval yang diberikan. Struktur ini bekerja mirip dengan struktur optlib :: genetic :: pre_birth :: vec_floatCheckChromoInterval dari tahap sebelumnya dari algoritma genetika.

StopChecker trait - stop kriteria

Setelah tahap seleksi, Anda perlu memeriksa apakah sudah waktunya untuk menghentikan algoritma genetika. Seperti yang telah disebutkan di atas, pada tahap ini, Anda juga dapat menggunakan berbagai algoritma penghentian. Untuk gangguan algoritma, objek bertanggung jawab atas penerapan sifat StopChecker , yang dinyatakan sebagai berikut:

 pub trait StopChecker<T: Clone> { fn can_stop(&mut self, population: &Population<T>) -> bool; }

Di sini metode can_stop () harus mengembalikan true jika algoritme dapat dihentikan, jika tidak metode ini akan kembali salah.

Modul optlib :: genetic :: stopchecker berisi beberapa struktur dengan kriteria berhenti dasar dan dua struktur untuk membuat kombinasi dari kriteria lain:

MaxIterations - pecahkan kriteria berdasarkan jumlah generasi. Algoritme genetik akan berhenti setelah sejumlah iterasi (generasi) yang diberikan.
GoalNotChange - kriteria istirahat yang menurutnya algoritma harus berhenti jika solusi baru tidak dapat ditemukan untuk sejumlah iterasi tertentu. Atau dengan kata lain, jika untuk beberapa generasi tertentu lebih banyak individu yang sukses tidak muncul.
Ambang - kriteria berhenti yang menurutnya algoritma genetika terputus jika nilai fungsi objektif dari solusi terbaik saat ini kurang dari nilai ambang yang ditentukan.
CompositeAll — , ( - StopChecker). , - , .
CompositeAny — , ( - StopChecker). , - , .

Logger —

Logger , , , . Logger :

 pub trait Logger<T: Clone> { ///       fn start(&mut self, _population: &Population<T>) {} ///     , ///           fn resume(&mut self, _population: &Population<T>) {} ///         /// (    ) fn next_iteration(&mut self, _population: &Population<T>) {} ///      fn finish(&mut self, _population: &Population<T>) {} }

optlib::genetic::logging , Logger:

Konstruktor struktur GeneticOptimizer , sebagai argumen terakhir, menerima vektor ciri-ciri Logger, yang memungkinkan Anda mengkonfigurasi output program secara fleksibel.

Fungsi untuk menguji algoritme pengoptimalan

Fungsi schweffel

Untuk menguji algoritme pengoptimalan, banyak fungsi diciptakan dengan banyak ekstrem lokal. Modul optlib :: testfunctions berisi beberapa fungsi, yang dapat diuji algoritma. Pada saat penulisan ini, modul optlib :: testfunctions hanya berisi dua fungsi.

Salah satu fungsi ini adalah fungsi Schweffel, yang ditulis di awal artikel. Sekali lagi, saya ingat bahwa fungsi ini ditulis sebagai berikut:

F (x) = 418.9829 N - \sum_{i = 1}^{N} x_{i} \sin (\sqrt{| x_{i} |})

$F(\boldsymbol x) = 418.9829N - \sum_{i=1}^{N}x_i \sin (\sqrt{|x_i|})$

x' = (420.9687, 420.9687, ...). .

optlib::testfunctions schwefel . N .

, , , , .

F (x) = \sum_{i = 1}^{N} (x_{i} - n)^{2}

$F(\boldsymbol x) = \sum_{i=1}^{N} (x_i - n)^2$

x' = (1.0, 2.0,… N). .

optlib::testfunctions paraboloid .

Kesimpulan

optlib , . ( optlib::genetic ), , , , .

optlib::genetic. . , , , , .

, . , ( , ..)

Selain itu, direncanakan untuk menambahkan fungsi analitis baru (selain fungsi Schweffel) untuk menguji algoritma pengoptimalan.

Sekali lagi, saya ingat tautan yang terkait dengan pustaka optlib:

Halaman di github - https://github.com/Jenyay/rust-optimization
Halaman di crates.io - https://crates.io/crates/optlib
Dokumentasi - https://docs.rs/optlib

Saya menantikan komentar, penambahan, dan komentar Anda.

Optlib Implementasi algoritma optimasi genetik di Rust