Hashing serbaguna dan sempurna

Kami memulai minggu ini dengan materi bermanfaat yang didedikasikan untuk peluncuran kursus "Algoritma untuk Pengembang" . Selamat membaca.



1. Ikhtisar

Hashing adalah alat praktis yang hebat, dengan teori yang menarik dan halus. Selain menggunakan data sebagai struktur kosa kata, hashing juga ditemukan di berbagai bidang, termasuk teori kriptografi dan kompleksitas. Dalam kuliah ini, kami menjelaskan dua konsep penting: hashing universal (juga dikenal sebagai keluarga universal fungsi hash) dan hashing ideal.

Materi yang disorot dalam kuliah ini meliputi:

• Pengaturan formal dan ide umum hashing.
• Hashing universal.
• Hashing sempurna.

2. Pendahuluan

Kami akan mempertimbangkan masalah utama dengan kamus yang telah kami diskusikan sebelumnya, dan mempertimbangkan dua versi: statis dan dinamis:

• Statis : diberi banyak elemen S, kami ingin menyimpannya sedemikian rupa sehingga kami dapat dengan cepat melakukan pencarian.
• Misalnya, kamus tetap.
• Dinamis : di sini kami memiliki urutan permintaan untuk penyisipan, pencarian, dan kemungkinan penghapusan. Kami ingin melakukan semua ini dengan efektif.

Untuk masalah pertama, kita bisa menggunakan array yang diurutkan dan pencarian biner. Untuk yang kedua, kita bisa menggunakan pohon pencarian seimbang. Namun, hashing menyediakan pendekatan alternatif, yang seringkali merupakan cara tercepat dan paling nyaman untuk menyelesaikan masalah ini. Sebagai contoh, misalkan Anda sedang menulis sebuah program untuk pencarian AI dan ingin menyimpan situasi yang telah Anda selesaikan (posisi di papan tulis atau elemen ruang keadaan) agar tidak mengulangi perhitungan yang sama ketika Anda bertemu lagi. Hashing menyediakan cara mudah untuk menyimpan informasi ini. Ada juga banyak aplikasi dalam kriptografi, jaringan, teori kompleksitas.

3. Dasar-dasar hash

Pengaturan formal untuk hashing adalah sebagai berikut.

• Kunci-kunci tersebut dimiliki oleh sejumlah besar U. (Misalnya, bayangkan bahwa U adalah kumpulan semua string dengan panjang maksimum 80 karakter ascii.)
• Ada beberapa kunci S di U yang benar-benar kita butuhkan (kunci bisa statis atau dinamis). Biarkan N = | S |. Bayangkan bahwa N jauh lebih kecil dari ukuran U. Misalnya, S adalah himpunan nama siswa di kelas yang jauh lebih kecil dari 128 ^ 80.
• Kami akan melakukan sisipan dan pencarian menggunakan array A dengan beberapa ukuran M dan fungsi hash h: U → {0, ..., M - 1}. Diberikan elemen x, ide hashing adalah bahwa kita ingin menyimpannya dalam A [h (x)]. Perhatikan bahwa jika Anda kecil (misalnya, string 2-karakter), maka Anda bisa menyimpan x dalam A [x], seperti dalam penyortiran blok. Masalahnya adalah U itu besar, jadi kita butuh fungsi hash.
• Kami membutuhkan metode untuk menyelesaikan tabrakan. Tabrakan adalah ketika h (x) = h (y) untuk dua kunci berbeda x dan y. Dalam kuliah ini, kami akan menangani tabrakan dengan mendefinisikan setiap elemen A sebagai daftar tertaut. Ada sejumlah metode lain, tetapi untuk masalah yang akan kita fokuskan di sini, ini yang paling cocok. Metode ini disebut metode chaining. Untuk memasukkan item, kami cukup meletakkannya di bagian atas daftar. Jika h adalah fungsi hash yang baik, maka kami berharap daftar akan kecil.

Salah satu hal hebat tentang hashing adalah bahwa semua operasi kamus sangat mudah diimplementasikan. Untuk mencari kunci x, cukup menghitung indeks i = h (x) dan kemudian pergi melalui daftar di A [i] sampai Anda menemukannya (atau keluar dari daftar). Untuk menyisipkan, cukup tempatkan item baru di bagian atas daftar. Untuk menghapus, Anda hanya perlu melakukan operasi hapus pada daftar yang ditautkan. Sekarang kita beralih ke pertanyaan: apa yang kita butuhkan untuk mencapai kinerja yang baik?

Properti yang diinginkan. Properti yang diinginkan utama untuk skema hash yang baik:

1. Kunci tersebar dengan baik sehingga kami tidak memiliki terlalu banyak tabrakan, karena tabrakan memengaruhi waktu pencarian dan penghapusan.
2. M = O (N): khususnya, kami ingin sirkuit kami mencapai properti (1) tanpa perlu ukuran tabel M menjadi jauh lebih besar dari jumlah elemen N.
3. Fungsi h harus dihitung dengan cepat. Dalam analisis kami hari ini, kami akan mempertimbangkan waktu untuk menghitung h (x) sebagai konstanta. Namun, perlu diingat bahwa itu tidak boleh terlalu rumit karena itu mempengaruhi waktu eksekusi keseluruhan.

Dengan ini, waktu pencarian untuk elemen x adalah O (ukuran daftar adalah A [h (x)]). Hal yang sama berlaku untuk penghapusan. Penyisipan membutuhkan waktu O (1) terlepas dari panjang daftar. Jadi, kami ingin menganalisis seberapa besar daftar ini.

Intuisi dasar: satu cara untuk mendistribusikan elemen dengan indah adalah dengan mendistribusikannya secara acak. Sayangnya, kita tidak bisa hanya menggunakan generator angka acak untuk memutuskan di mana mengarahkan elemen berikutnya, karena dengan begitu kita tidak akan pernah bisa menemukannya lagi. Jadi, kami ingin h menjadi sesuatu yang "pseudo-random" dalam arti formal.

Sekarang kami akan menyajikan beberapa kabar buruk, dan kemudian kabar baik.

Pernyataan 1 (Berita Buruk) Untuk fungsi hash h jika | U | ≥ (N −1) M +1, ada himpunan elemen S dari N yang semuanya hash di satu tempat.

Bukti: dengan prinsip Dirichlet. Khususnya, untuk mempertimbangkan titik tandingan, jika setiap lokasi memiliki tidak lebih dari N - 1 elemen U yang hash, maka U dapat memiliki ukuran tidak lebih dari M (N - 1).

Ini sebagian mengapa hashing tampak begitu misterius - bagaimana bisa dikatakan bahwa hashing bagus jika untuk fungsi hash apa pun Anda dapat memikirkan cara untuk mencegahnya? Salah satu jawabannya adalah bahwa ada banyak fungsi hash sederhana yang bekerja dengan baik dalam praktik untuk set S yang khas.

Inilah ide kuncinya: mari gunakan pengacakan di konstruk h kami, mirip dengan quicksort acak. (Tak perlu dikatakan, h akan menjadi fungsi deterministik). Kami akan menunjukkan bahwa untuk setiap urutan penyisipan dan operasi pencarian (kita tidak perlu berasumsi bahwa himpunan elemen yang dimasukkan S adalah acak), jika kita memilih h dengan cara probabilistik ini, kinerja h dalam urutan ini akan baik dalam mengantisipasi. Dengan demikian, ini adalah jaminan yang sama seperti dalam quicksort atau perangkap acak. Secara khusus, ini adalah ide hashing universal.

Setelah kami mengembangkan ide ini, kami akan menggunakannya untuk aplikasi yang sangat menyenangkan yang disebut "hashing sempurna".

4. hashing Universal

Definisi 1. Algoritma acak H untuk membangun fungsi hash h: U → {1, ..., M}
universal jika untuk semua x! = y di dalam U yang kita miliki



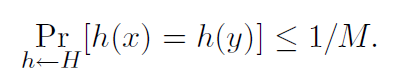
Kita juga dapat mengatakan bahwa himpunan fungsi hash adalah keluarga universal dari fungsi hash jika prosedur "pilih acak h ∈ H" bersifat universal. (Di sini kami mengidentifikasi set fungsi dengan distribusi seragam atas set.)

Teorema 2. Jika H adalah universal, maka untuk setiap himpunan S ⊆ U dengan ukuran N, untuk x ∈ U (misalnya, yang dapat kita cari), jika kita membangun h secara acak sesuai dengan H, jumlah tumbukan yang diharapkan antara x dan lainnya elemen dalam S tidak lebih dari N / M.

Bukti: setiap y ∈ S (y! = X) memiliki paling tidak 1 / M peluang tabrakan dengan x dengan definisi "universal". Jadi

• Biarkan Cxy = 1 jika x dan y bertabrakan, dan 0 sebaliknya.
• Biarkan Cx menunjukkan jumlah total tabrakan untuk x. Jadi, Cx = Py∈S, y! = X Cxy.
• Kita tahu bahwa E [Cxy] = Pr (x dan y bertabrakan) ≤ 1 / M.
• Jadi, dalam linearitas ekspektasi, E [Cx] = Py E [Cxy] <N / M.

Sekarang kita mendapatkan akibat wajar berikut.

Konsekuensi 3. Jika H bersifat universal, maka untuk setiap urutan operasi penyisipan, pencarian, dan penghapusan L, di mana tidak boleh ada lebih dari elemen M dalam suatu sistem pada suatu waktu, total biaya operasi L yang diharapkan untuk acak h ∈ H hanya O (L) (melihat waktu) untuk menghitung h sebagai konstanta).

Bukti: untuk setiap operasi tertentu dalam urutan, biaya yang diharapkan adalah konstan oleh Teorema 2, sehingga total biaya yang diharapkan dari operasi L adalah O (L) dalam linearitas ekspektasi.

Pertanyaan: bisakah kita benar-benar membangun H universal? Jika tidak, maka ini semua tidak ada gunanya. Untungnya, jawabannya adalah ya.

4.1. Menciptakan keluarga hash universal: metode matriks

Misalkan kuncinya panjang u-bit. Katakanlah, ukuran tabel M sama dengan derajat 2, oleh karena itu, indeks b-bit panjang dengan M = 2b.

Apa yang akan kita lakukan adalah memilih h sebagai matriks acak 0/1 b-by-u dan mendefinisikan h (x) = hx, di mana kita menambahkan mod 2. Matriks ini pendek dan tebal. Sebagai contoh:



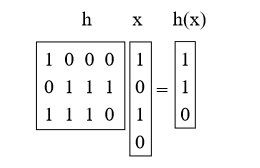
Proposisi 4. Untuk x! = Y Prh [h (x) = h (y)] = 1 / M = 1 / 2b.

Bukti: Pertama, apa artinya mengalikan x dengan x? Kita dapat menganggapnya sebagai menambahkan beberapa kolom h (melakukan penambahan vektor mod 2), di mana 1 bit dalam x menunjukkan mana yang akan ditambahkan. (misalnya, kami menambahkan kolom 1 dan 3 dari h di atas)

Sekarang ambil pasangan kunci acak x, y sedemikian rupa sehingga x! = Y. Mereka pasti berbeda di suatu tempat, sehingga, katakanlah, mereka berbeda dalam koordinat ith, dan untuk konkretnya kita katakan xi = 0 dan yi = 1. Bayangkan bahwa kita pertama-tama memilih semua h kecuali kolom ke-i. Untuk sisa sampel kolom ke-i, h (x) ditetapkan. Namun, masing-masing 2b pengaturan yang berbeda pada kolom ke-i memberikan nilai h (y) yang berbeda (khususnya, setiap kali kita mengubah sedikit dalam kolom ini, kita mengubah bit yang sesuai menjadi h (y)). Jadi ada kemungkinan 1 / 2b bahwa h (x) = h (y).

Ada metode lain untuk membangun keluarga hash universal, yang juga didasarkan pada penggandaan bilangan prima (lihat Bagian 6.1).

Pertanyaan selanjutnya yang akan kita pertimbangkan: jika kita memperbaiki set S, dapatkah kita menemukan fungsi hash sehingga semua pencarian akan memiliki waktu yang konstan? Jawabannya adalah ya, dan ini mengarah ke topik hashing sempurna.

5. hashing sempurna

Kami mengatakan bahwa fungsi hash ideal untuk S jika semua pencarian terjadi di O (1). Berikut adalah dua cara untuk membangun fungsi hash yang sempurna untuk himpunan S.

5.1 Metode 1: solusi di ruang O (N2)

Katakanlah kita ingin memiliki tabel yang ukurannya kuadratik dalam ukuran N dari kamus kita S. Maka di sini adalah metode sederhana untuk membangun fungsi hash yang ideal. Biarkan H menjadi universal dan M = N2. Kemudian pilih saja h acak dari H dan coba! Pernyataannya adalah bahwa setidaknya ada kemungkinan 50% bahwa dia tidak akan mengalami tabrakan.

Proposisi 5. Jika H adalah universal dan M = N2, maka Prh∼H (tidak ada tabrakan dalam S) ≥ 1/2.

Bukti:

• Berapa banyak pasangan (x, y) yang ada di S? Jawabannya adalah:
• Untuk setiap pasangan, probabilitas tumbukan mereka adalah ≤ 1 / M menurut definisi universalitas.
• Jadi Pr (ada tabrakan) ≤ / M <1/2.

Ini seperti sisi lain dari "paradoks ulang tahun". Jika jumlah hari jauh lebih besar dari jumlah orang yang dikuadratkan, maka ada kemungkinan yang masuk akal bahwa tidak ada pasangan yang akan berulang tahun.

Jadi, kami hanya memilih h acak dari H, dan jika ada tabrakan, kami hanya memilih h baru. Rata-rata, kita hanya perlu melakukan ini dua kali. Sekarang, bagaimana jika kita hanya ingin menggunakan ruang O (N)?

5.2 Metode 2: solusi di ruang O (N)

Pertanyaan apakah mungkin untuk mencapai hashing sempurna di ruang O (N) telah terbuka untuk beberapa waktu: "Haruskah tabel diurutkan?" Artinya, untuk set tetap, Anda bisa mendapatkan waktu pencarian konstan hanya dengan ruang linear? Ada serangkaian upaya yang semakin kompleks, sampai akhirnya diselesaikan dengan ide bagus fungsi hash universal dalam skema dua tingkat.

Metodenya adalah sebagai berikut. Pertama, kita akan hash ke tabel ukuran N menggunakan hashing universal. Ini akan menyebabkan beberapa tabrakan (kecuali jika kita beruntung). Namun, kami mengulangi setiap keranjang menggunakan metode 1, mengkuadratkan ukuran keranjang untuk mendapatkan tabrakan nol. Dengan demikian, skema terdiri dalam kenyataan bahwa kita memiliki fungsi hash dari tingkat pertama h dan tabel A dari tingkat pertama, dan kemudian fungsi hash N dari tingkat kedua h1, ..., hN dan N dari tabel tingkat kedua A1, ..., . ... Untuk menemukan elemen x, pertama-tama kita menghitung i = h (x), dan kemudian menemukan elemen dalam Ai [hi (x)]. (Jika Anda melakukan ini dalam praktiknya, Anda dapat mengatur bendera sehingga Anda akan mengambil langkah kedua hanya jika benar-benar ada konflik dengan indeks i, jika tidak, Anda hanya akan menempatkan x sendiri di A [i], tetapi mari jangan khawatir tentang itu di sini.)

Katakan fungsi hash h hashes n elemen S ke lokasi i. Kami telah membuktikan (dengan menganalisis metode 1) bahwa kami dapat menemukan h1, ..., hN, sehingga total ruang yang digunakan dalam tabel sekunder adalah Pi (ni) 2. Tetap menunjukkan bahwa kami dapat menemukan fungsi tingkat pertama h sedemikian rupa sehingga Pi (ni) 2 = O (N). Bahkan, kami akan menunjukkan hal berikut:

Teorema 6. Jika kita memilih titik awal h dari set universal H, maka

Pr[X i (ni)2 > 4N] < 1/2. 

Bukti. Mari kita buktikan dengan menunjukkan bahwa E [Pi (ni) 2] <2N. Ini menyiratkan apa yang kita inginkan dari ketidaksetaraan Markov. (Jika ada kemungkinan bahkan 1/2 bahwa jumlahnya bisa lebih dari 4N, fakta ini saja akan berarti bahwa ekspektasi harus lebih dari 2N. Jadi, jika ekspektasinya kurang dari 2N, probabilitas kegagalan harus lebih kecil. 1/2.)

Sekarang, trik rumitnya adalah bahwa salah satu cara untuk menghitung jumlah ini adalah dengan menghitung jumlah pasangan berurutan yang memiliki tabrakan, termasuk tabrakan dengan diri sendiri. Misalnya, jika keranjang memiliki {d, e, f}, maka d akan memiliki konflik dengan masing-masing {d, e, f}, e akan memiliki konflik dengan masing-masing {d, e, f}, dan f akan memiliki konflik dengan masing-masing dari {d, e, f}, jadi kita mendapatkan 9. Jadi, kita memiliki:

 E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N) 

Jadi, kami hanya mencoba h acak dari H sampai kami menemukan satu sehingga Pi n2 i <4N, dan kemudian memperbaiki fungsi ini h, kami menemukan N fungsi hash sekunder h1, ..., hN seperti pada metode 1.

6. Diskusi lebih lanjut

6.1 Metode hashing universal lainnya

Berikut adalah metode lain untuk membangun fungsi hash universal, yang sedikit lebih efisien daripada metode matriks yang diberikan sebelumnya.

Dalam metode matriks, kami menganggap kunci sebagai vektor bit. Dalam metode ini, kita akan mempertimbangkan kunci x sebagai vektor bilangan bulat [x1, x2, ..., xk] dengan satu-satunya persyaratan bahwa setiap xi berada dalam kisaran {0, 1, ..., M-1}. Misalnya, jika kita memiliki string hash dengan panjang k, maka xi dapat menjadi karakter ke-i (jika ukuran tabel kita setidaknya 256) atau pasangan karakter ke-5 (jika ukuran tabel kita setidaknya 65536). Selain itu, kami akan meminta ukuran meja kami M menjadi prima. Untuk memilih fungsi hash h, kami memilih k angka acak r1, r2, ..., pk dari {0, 1, ..., M - 1} dan menentukan:

 h(x) = r1x1 + r2x2 + . . . + rkxk mod M. 

Bukti bahwa metode ini bersifat universal dibangun dengan cara yang sama seperti bukti metode matriks. Biarkan x dan y menjadi dua kunci yang berbeda. Kami ingin menunjukkan bahwa Prh (h (x) = h (y)) ≤ 1 / M. Karena x! = Y, harus ada kasus ketika ada beberapa indeks i sedemikian rupa sehingga xi! = Yi. Sekarang bayangkan Anda pertama kali memilih semua angka acak rj untuk j! = I. Biarkan h ′ (x) = Pj6 = i rjxj. Jadi, dengan memilih ri, kita mendapatkan h (x) = h ′ (x) + rixi. Ini berarti bahwa kita memiliki konflik antara x dan y kapan tepatnya

 h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M. 

Karena M adalah bilangan prima, membaginya dengan nilai bukan nol dari mod M adalah valid (setiap bilangan bulat dari 1 hingga M-1 memiliki modul invers multiplikatif M), yang berarti bahwa ada tepat satu nilai ri modulo M dimana persamaan di atas berlaku true, yaitu ri = (h ′ (y) - h ′ (x)) / (xi - yi) mod M. Dengan demikian, probabilitas kejadian ini tepat 1 / M.

6.2 Penggunaan hashing lainnya

Misalkan kita memiliki urutan elemen yang panjang, dan kita ingin melihat berapa banyak elemen yang berbeda dalam daftar. Apakah ada cara yang baik untuk melakukan ini?

Salah satu caranya adalah dengan membuat tabel hash, dan kemudian membuat satu melewati urutan dengan melakukan pencarian untuk setiap elemen dan kemudian memasukkan jika belum ada dalam tabel. Jumlah elemen individu hanyalah jumlah sisipan.

Dan sekarang, bagaimana jika daftar itu sangat besar dan kami tidak punya tempat untuk menyimpannya, tetapi jawaban perkiraan cocok untuk kami. Sebagai contoh, bayangkan kita adalah router dan amati berapa banyak paket yang dilalui, dan kami ingin (kurang-lebih) melihat berapa banyak alamat IP sumber berbeda yang ada.

Ini adalah ide yang bagus: katakanlah kita memiliki fungsi hash h yang berperilaku seperti fungsi acak, dan mari kita bayangkan bahwa h (x) adalah bilangan real dari 0 hingga 1. Satu hal yang bisa kita lakukan adalah tetap melacak minimum nilai hash telah diproduksi sejauh ini (jadi kami tidak akan memiliki meja sama sekali). Misalnya, jika kuncinya adalah 3,10,3,3,12,10,12 dan h (3) = 0,4, h (10) = 0,2, h (12) = 0,7, maka kita mendapatkan 0, 2.

Faktanya adalah bahwa jika kita memilih N angka acak dalam [0, 1], nilai minimum yang diharapkan adalah 1 / (N + 1). Selain itu, ada kemungkinan bagus bahwa itu cukup dekat (kita dapat meningkatkan perkiraan kami dengan menjalankan beberapa fungsi hash dan mengambil median dari posisi terendah).

Pertanyaan: mengapa menggunakan fungsi hash, dan tidak hanya memilih nomor acak setiap kali? Ini karena kami peduli dengan jumlah elemen yang berbeda, dan bukan hanya jumlah total elemen (masalah ini jauh lebih sederhana: cukup gunakan penghitung ...).

Teman-teman, apakah artikel ini bermanfaat bagi Anda? Tuliskan di komentar dan bergabunglah dengan hari terbuka , yang akan diadakan pada tanggal 25 April.