❕ 📹 🧔 Tapi bukankah kita melambaikan komunikasi optik? Laser, luar angkasa, CubeSat 🈳 👵🏼 🍏

Materi yang diuraikan di bawah ini adalah hasil kerja sama dengan para guru TU Ilmenau sebagai bagian dari proyek kursus lokal (Proyek Penelitian Lanjut). Pengalaman itu menarik, tetapi bukan tanpa kesulitan tertentu. Kami melakukan proyek ini (dan satu lagi) dengan calon pengantin saya - ya, jadi kami beruntung belajar bersama dan magang di Jerman. Sebenarnya, dialah yang melakukan bagian pekerjaan ini lebih jauh, tetapi saya ingin mempopulerkan topik ini.

Jadi, suatu hari kami membuat janji untuk memilih topik untuk karya ilmiah ...

Latar belakang pendek (pada wajah)

Guru Jerman # 1 : Oh, saya dengar Anda mempelajari satelit format CubeSat di sana?

Saya dan calon istri saya : Ya, bisa dibilang ...

N.p. 1 : Hebat! Tetapi bagaimana jika Anda mencoba mempertimbangkan komunikasi optik antara satelit? Saya tahu bahwa dalam beberapa kasus, optik memberikan kinerja energi terbaik, untuk satelit sekecil itu, saya menganggap masalah ini sangat penting. Saya punya satu teman yang secara profesional terlibat dalam optik nirkabel. Saya pikir ini akan menjadi proyek yang menarik!

Kami : Kedengarannya menarik!

(beberapa waktu berlalu)

Pertemuan dengan guru bahasa Jerman nomor 2 .

N.p. 2 : Ya, semua ini, tentu saja, bagus, tetapi satelit seperti apa? Massa yang begitu kecil? Bisakah mereka berkomunikasi? Siapa yang menyarankan ini? Dipahami ... Rupanya, kita tidak akan melihatnya di pertemuan ini. Pergi mencari contoh dunia nyata - Saya belum percaya.

Dan kami berangkat ...

Dan, untuk kesenangan mereka, mereka bahkan menemukan seluruh artikel yang dikhususkan untuk topik ini. Perbedaan penting adalah bahwa komunikasi melalui optik seharusnya dengan Bumi, dan bukan antara satelit. Ini sangat penting karena:

semua jenis hamburan dan gangguan, tentu saja, dalam hal ini lebih banyak,
Namun, penerima di Bumi dapat diatur cukup besar, dan pemancar cukup akurat. Dan segmen ruang, Anda mengerti, sedikit rumit.

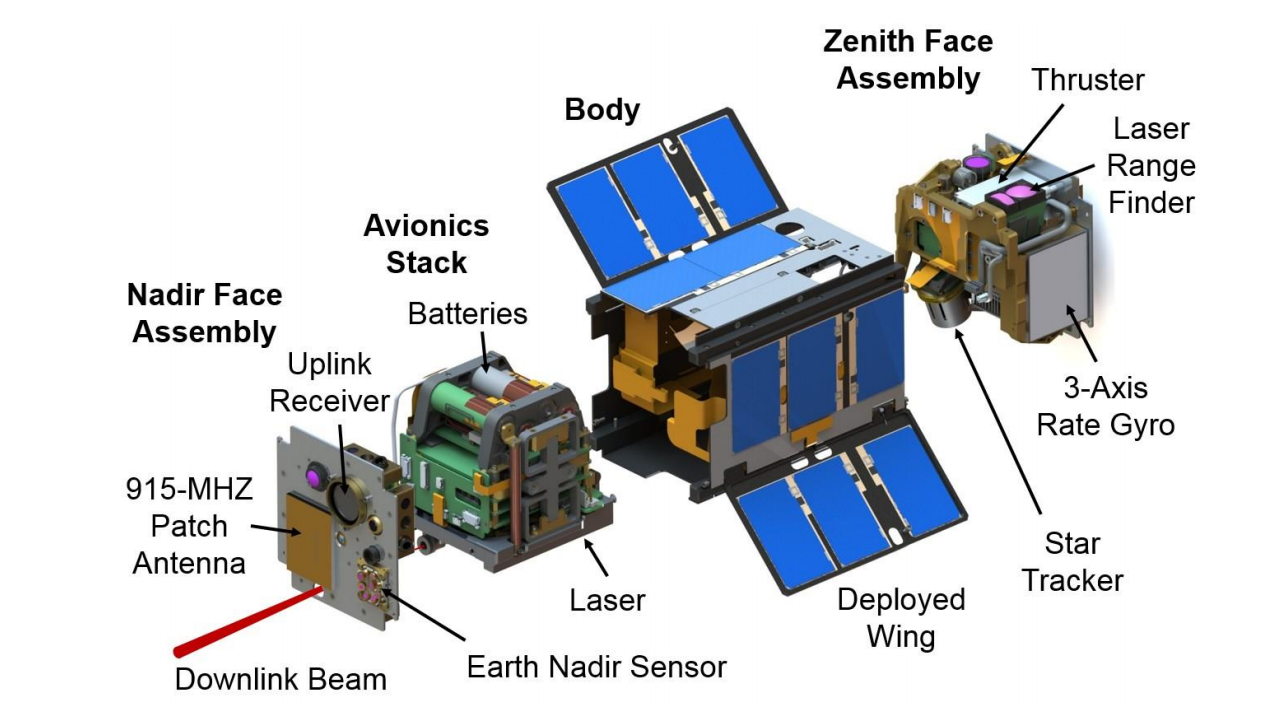
Fig. 1. Representasi skematis dari satelit AeroCube-OCSD [1].

Tapi itu sudah sesuatu, dan kami membuat janji lagi.

N.p. 2 : Baik, baik, sejak NASA ... Mari kita coba menghitung anggaran energi dan membandingkannya dengan anggaran energi tautan radio. Artikel terkait untuk dibuang?

Dan dia membuang artikelnya [2] (saya akan merujuk beberapa kali hari ini) dan beberapa artikel oleh penulis lain untuk pemahaman umum tentang masalah ini.

Berapakah anggaran energi dari jalur optik antar-satelit?

Anggaran Energi Optik Nirkabel

Tapi itu menyiratkan dengan sendirinya, secara umum, hal yang sama seperti biasa (daya pemancar yang diperlukan, daya terima, SNR, dll.) - hanya suara-suara dianggap sedikit lebih menarik daripada dalam hal komunikasi radio ...

Mari kita mulai membuat model - ini akan menjadi sedikit lebih jelas:

import numpy as np from matplotlib.pyplot import plot, grid, xlabel, ylabel, legend import matplotlib.pyplot as plt from scipy import special

Misalkan kita memiliki sistem seperti itu:

 #initial parameters for optical case R = 100*1e3 #distance between objects, eg satellites, in m (100 km) Bit_rate = 1e6 #bit rate (1 Mbps) h = 6.62607004*1e-34 # Planck constant c = 299792458 #speed of light wavelength_opt = 1550*1e-9 #optical wavelength freq_opt = c/wavelength_opt #optical frequency Ptx_opt = 1 #transmitter power in Watts Ptx_opt_dBm = 10*np.log10(Ptx_opt*1e3) #transmitter power in dBm

Kami menetapkan sekumpulan diameter tertentu dari penerima optik (pada kenyataannya, lensa) - kami perhatikan batasan ukuran satelit itu sendiri:

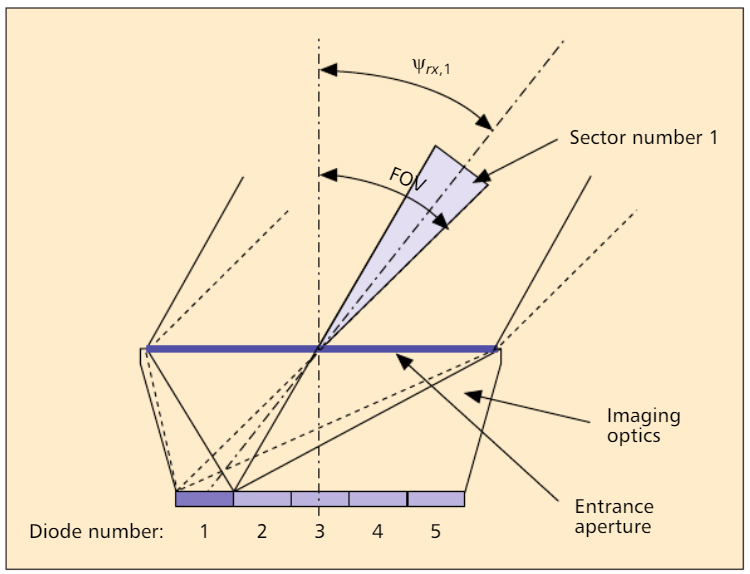
 a = [i for i in range(0,50,5)] a = np.array(a)*1e-3 #diameter of the receiver (in meters) a[0] = 1*1e-3 a_m = a*100 # for figures (in cm)

Fig. 2. Diagram skematik dari photodetector: ditampilkan sebagai contoh untuk sektor No. 1, sudut-sudut insiden yang ditampilkan pada fotodioda No. 1 [2].

Dan beberapa kemungkinan sudut divergensi sinar laser (pemancar kami):

 div_ang = [0.2*1e-3, 0.5*1e-3, 2*1e-3, 5*1e-3, 7*1e-3] div_ang = np.array(div_ang) #half of divergence angle

Fig. 3. Ilustrasi sudut divergensi sinar laser.

Daya pada input penerima (daya yang diterima) dapat dihitung dengan rumus [2] :

$P_ {rx} = \ frac {A_ {rx}} {2 \ pi R ^ 2} \ kiri (1 - \ frac {ln2} {ln (cos \ theta_ {div})} \ kanan) P_ {tx} \ quad [W]$

dimana $A_ {rx} = \ frac {d_ {rx} ^ 2 \ pi} {4}$ Apakah area penerimaan, $d_ {rx}$ - diameter lensa penerima, $R$ - Jarak antar satelit, $\ theta_ {div}$ Adalah setengah sudut divergensi dan $P_ {tx}$ - Daya yang ditransmisikan.

 Prx_opt_dBm = np.zeros((len(div_ang), len(a))) Prx_opt = np.zeros((len(div_ang), len(a))) Pathloss_dBm = np.zeros((len(div_ang), len(a))) Pathloss = np.zeros((len(div_ang), len(a))) Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #received power Prx_opt[f,:] = (Ptx_opt*Arx_m2)/ (2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Prx_opt_dBm[f,:] = 10*np.log10(Prx_opt[f,:]*1e3) #path loss Pathloss[f,:] = (Arx_m2)/(2*np.pi*(R**2))\ *(1-(np.log(2)/np.log(np.cos(dvangl)))) Pathloss_dBm[f,:] = 10*np.log10(Pathloss[f,:]*1000)

Oke, sesuatu sudah ada di sana. Tetapi seberapa banyak semua ini secara fisik dapat diwujudkan?

Keterbatasan Sensitivitas

Batas kuantum

Ingat rumus energi foton:

$E = hf \ quad \ kiri [m ^ 2 kg / s ^ 2 \ kanan]$

dimana $h$ = 6.62607004e-34 $m ^ 2 kg / s$ Apakah konstanta Planck , dan $f$ - Frekuensi pembawa (Hz).

Ini akan diikuti oleh heuristik kecil yang diambil dari konsultasi kami. Jika seseorang mengetahui pembenaran atau bantahan teoretis - silakan bagikan!

Energi yang diperlukan (energi minimum per bit informasi di sisi penerima untuk mendeteksi setidaknya sesuatu):

$E_ {req, Q} = N_ {ph} hf \ quad \ kiri [m ^ 2 kg / s ^ 2 \ kanan]$

dimana $N_ {ph}$ - jumlah rata-rata foton yang diperlukan untuk mendeteksi 1 bit informasi.

Energi teoretis untuk pulsa optik:

 E_theor = 10*h*freq_opt

Nilai energi yang lebih realistis untuk pulsa optik (dioda APD ):

 E_real_APD = 1000*h*freq_opt

Nilai energi yang lebih realistis untuk pulsa optik ( PIN diode):

 E_real_PIN = 10000*h*freq_opt

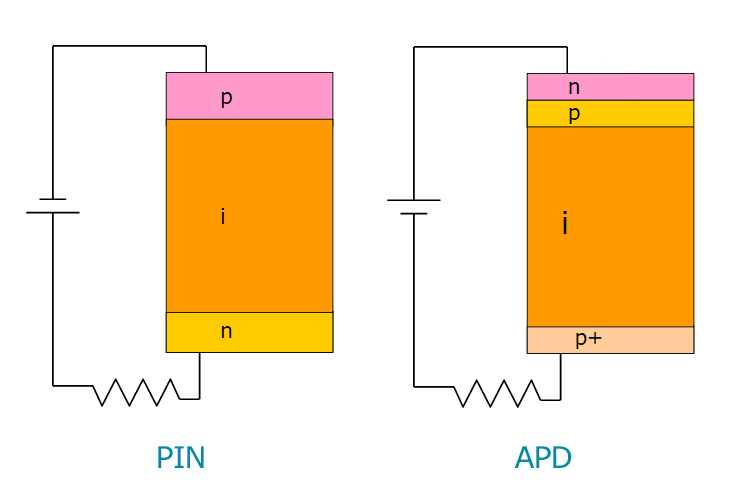
Fig. 4. Sirkuit fotodioda sedang dipertimbangkan.

Diperlukan (minimum) menerima daya (sensitivitas maksimum):

$P_ {req, Q} = 10 \ log_ {10} \ kiri (\ frac {E_ {req, Q} B} {10 ^ {- 3}} \ kanan) = 10 \ log_ {10} \ kiri (\ frac {E_ {req, Q} R_b} {10 ^ {- 3}} \ kanan) \ quad [dBm]$

dimana $B$ Apakah bandwidth saluran komunikasi, dan $R_b$ Apakah bitrate.

 P_req_theor = 10*np.log10(E_theor*Bit_rate*1000) P_req_real_APD = 10*np.log10(E_real_APD*Bit_rate*1000) P_req_real_PIN = 10*np.log10(E_real_PIN*Bit_rate*1000)

Tapi itu tidak semua: modulasi juga membuat kontribusinya yang membatasi.

Batas Probabilitas Kesalahan

Sebagai titik awal kami akan mempertimbangkan modulasi OOK (On-off Keying).

Fig. 5. Ilustrasi prinsip modulasi OOK.

Probabilitas kesalahan ( BER ) untuk itu adalah [2]:

$P_b = \ frac {1} {2} ercf \ kiri (\ sqrt {\ frac {SNR} {2}} \ kanan) = \ frac {1} {2} ercf \ kiri (\ sqrt {\ frac {P_ { req} ^ 2 \ gamma ^ 2} {2 \ sigma ^ 2}} \ benar)$

dimana $SNR$ Apakah rasio signal-to-noise, $\ sigma ^ 2$ Apakah varians derau (yaitu daya derau), dan $\ gamma$ Adalah sensitivitas fotodioda ( responsif fotodioda ).

BER untuk OOK (PIN diode):

$P_ {b, PIN} = \ frac {1} {2} ercf \ kiri (\ frac {\ gamma P_ {req, PIN}} {\ sqrt {2 \ sigma_ {PIN} ^ 2}} \ kanan)$

Dan karena itu:

$P_ {req, PIN} = \ frac {erfcinv (2P_b) \ sqrt {2 \ sigma_ {PIN} ^ 2}} {\ gamma} \ quad [W]$

BER untuk OOK (dioda APD):

$P_ {b, APD} = \ frac {1} {2} ercf \ kiri (\ frac {\ gamma M P_ {req, APD}} {\ sqrt {2 \ sigma_ {APD} ^ 2}} \ kanan)$

Dan karena itu:

$P_ {req, APD} = \ frac {erfcinv (2P_b) \ sqrt {2 \ sigma_ {APD} ^ 2}} {\ gamma M} \ quad [W]$

dimana $M.$ - Ini adalah beberapa keuntungan referensi.

Kekuatan kebisingan

Seperti yang sudah Anda duga, kebisingan juga akan dihitung sedikit berbeda.

Kekuatan suara untuk dioda PIN

Kebisingan termal dapat dihitung dengan rumus [3, p 11] :

$\ sigma_ {PIN} ^ 2 = \ kiri (\ frac {4kT} {R_f} + 2qI_ {BE} \ kanan) I_2R_b = N_0 + 2qI_ {BE} I_2R_b \ quad [W]$

dimana $T = 290 K$ , $k = 1.38064852e-23$ - Konstanta Boltzmann $R_f = \ frac {100} {2 \ pi C_d R_b}$ - resistensi langsung $C_d$ - kapasitas fotodioda, $q$ Apakah muatan elektron, $I_ {BE} = \ frac {I_C} {\ beta}$ - basis-emitor saat ini ( basis-emitor atau kebocoran atau arus bias ), $I_2$ - nilai integral Personick (- Saya menyerah, saya tidak menemukan terjemahan yang memadai, tolong katakan padaku) untuk noise termal, $R_b$ - bit rate $N_0$ - Kepadatan spektral kebisingan.

 Cd = 2*1e-12 #capacitance of the photodiode T = 290 #absolute temperature Rf = 100/(Cd*2*np.pi*Bit_rate) #photodiode resistance k = 1.38064852*1e-23 #Bolzman constant I2 = 0.562 #depends on filter (Personick integral) for match filter q = 1.60217662*1e-19 #electron charge Ibe = (0.25*1e-3)/200 #RESULT thermal_Noise_variance_add = 2*q*Ibe*I2*Bit_rate N_0 = 4*k*T/Rf #thermal noise density for PIN thermal_Noise_variance = N_0*Bit_rate*I2

Kekuatan suara untuk dioda APD

Bersiaplah untuk dioda ini - banyak huruf Latin:

$\ sigma_ {APD} ^ 2 = \ frac {4kT} {R_f} I_2R_b + 2qI_dM_ {Si} ^ 2F_ {Si} I_2R_b = N_0 + 2qI_2R_b (I_ {BE} + M_ {Si} I_d {Si} I_d) \ sekitar N_0 + 2qI_2I_dR_bM_ {Si} ^ 2F_ {Si} \ quad [W]$

dimana $I_d$ - Arus gelap (arus gelap), $M_ {Si}$ Merupakan gain tipikal (silikon), $F_ {Si}$ - faktor kebisingan berlebih.

Parameter dikumpulkan dari berikut ini:

Dalam tulisan ini, kebisingan dari transistor efek medan input (noise FET input) dan kebisingan beban transistor efek medan input (noise dari beban input FET) tidak diperhitungkan. Baca lebih lanjut tentang istilah-istilah ini dalam [3, p 15] .

 Id = 0.05*10e-9 #dark current (500e-12) M_Si = 100 #typical gain F_Si = 7.9 #excess noise factor apd_noise_Si = 2*q*Id*I2*Bit_rate*(M_Si**2)*F_Si #noise

Pemodelan

Daya diterima

Kami mengganti semua yang diklarifikasi dalam formula kami:

 r = 0.53 #A/W photodiode responsivity Pb = 10e-9 #Bit error rate (BER) P_req_pin = 10*np.log10((special.erfcinv(2*Pb)* np.sqrt(2*(thermal_Noise_variance+thermal_Noise_variance_add))/(r))*1e3) #in dBm P_req_apd_lin = special.erfcinv(2*Pb)*np.sqrt(2*(thermal_Noise_variance+apd_noise_Si))/(r*M_Si) P_req_apd = 10*np.log10(P_req_apd_lin*1e3) #in dBm fig = plt.figure(figsize=(10, 7), dpi=300) req_theor = np.ones((len(a_m),))*P_req_theor req_real_APD = np.ones((len(a_m),))*P_req_real_APD req_real_PIN = np.ones((len(a_m),))*P_req_real_PIN PIN = np.ones((len(a_m),))*P_req_pin APD = np.ones((len(a_m),))*P_req_apd a_m = a_m.reshape((10,)) plot(a_m, Prx_opt_dBm[0,:],'-o', label = '0.2 mrad') plot(a_m, Prx_opt_dBm[1,:],'-o', label = '0.5 mrad') plot(a_m, Prx_opt_dBm[2,:],'-o', label = '2 mrad') plot(a_m, Prx_opt_dBm[3,:],'-o', label = '5 mrad') plot(a_m, Prx_opt_dBm[4,:],'-o', label = '7 mrad') plot(a_m, req_theor,'k--', label = 'Sensitivity limit (theory)') plot(a_m, req_real_APD, '--*', label = 'Sensitivity limit (APD)') plot(a_m, req_real_PIN, '--', label = 'Sensitivity limit (PIN)') plot(a_m, APD, '-*',label = '1e-9 OOK BER limit (APD)') plot(a_m, PIN, label = '1e-9 OOK BER limit (PIN)') plt.gca().invert_yaxis() xlabel('Rx diameter (cm)'); ylabel('Prx and Preq (dBm)') legend() grid() plt.show()

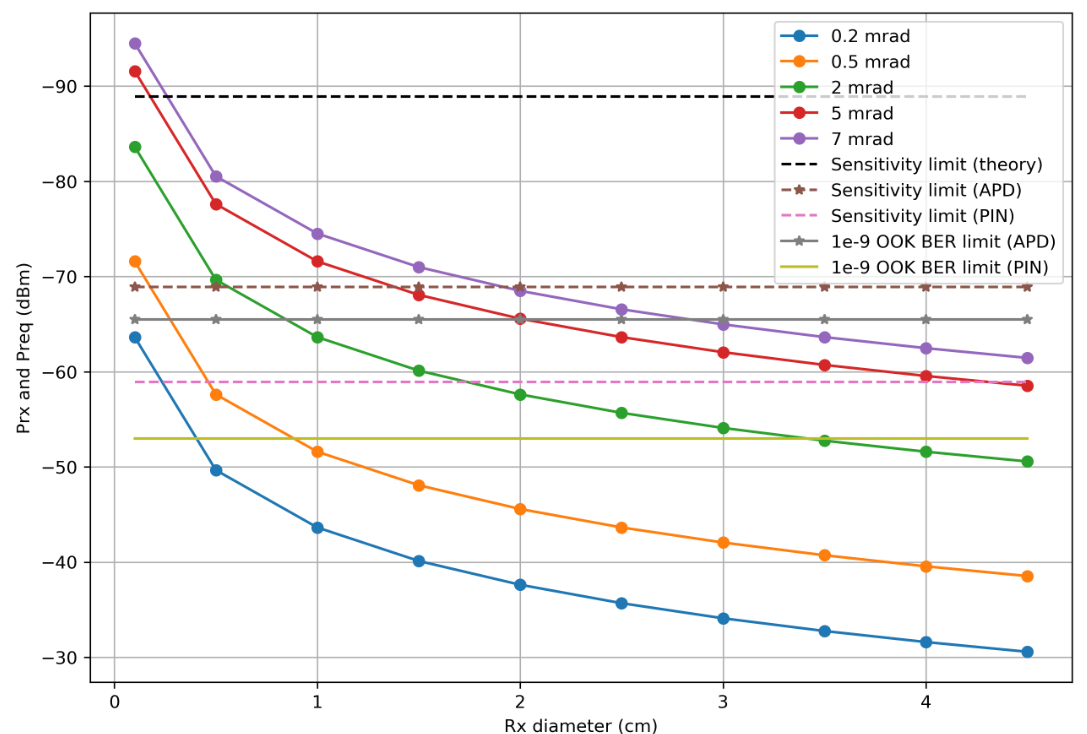
Mari kita jelaskan: Anda perlu melihat bagian-bagian kurva yang terletak di bawah garis horizontal yang sesuai.

Daya yang ditransmisikan

Dan sekarang mari kita lihat masalah yang berlawanan: kita memperbaiki daya pada sisi penerima dan melihat jenis daya apa yang perlu diterapkan pada sisi transmisi:

$P_ {tx, dBm} = P_ {rx, dBm} + | L | + | L_ {add} |$

dimana $L = 10 \ log_ {10} \ kiri [\ frac {A_ {rx}} {2 \ pi R ^ 2} \ kiri (1 - \ frac {ln2} {ln (cos \ theta_ {div})} \ kanan ) \ benar]$ Apakah jalannya pelemahan , dan $L_ {add}$ - Ini adalah margin untuk kerugian.

 Prx_req_dB_APD = -65.5 Prx_req_dB_PIN = -52.9 margin = 5 Arx_m2 = np.zeros((len(a))) Ptx_variable_APD = np.zeros((len(div_ang), len(a))) Ptx_variable_PIN = np.zeros((len(div_ang), len(a))) #area rx Arx_m2 = (np.pi/4)*(a**2) for f, dvangl in enumerate(div_ang): #Ptx required Ptx_variable_APD[f,:] = Prx_req_dB_APD + np.abs(Pathloss_dBm[f,:]) + margin; Ptx_variable_PIN[f,:] = Prx_req_dB_PIN + np.abs(Pathloss_dBm[f,:]) + margin; fig = plt.figure(figsize=(10, 7), dpi=300) plot(a_m, Ptx_variable_APD[0,:],'-o', label = 'APD, 0.2 mrad') plot(a_m, Ptx_variable_PIN[0,:],'-*', label = 'PIN, 0.2 mrad') plot(a_m, Ptx_variable_APD[1,:],'-o', label = 'APD, 0.5 mrad') plot(a_m, Ptx_variable_PIN[1,:],'-*', label = 'PIN, 0.5 mrad') plot(a_m, Ptx_variable_APD[2,:],'-o', label = 'APD, 2 mrad') plot(a_m, Ptx_variable_PIN[2,:],'-*', label = 'PIN, 2 mrad') xlabel('Rx diameter (cm)'); ylabel('P_tx (dBm)') legend() grid() plt.show()

Perbandingan dengan kasus saluran antar-satelit elektromagnetik dapat ditemukan di artikel jurnal kami . Ini juga menjelaskan alasan mengapa, pada akhirnya, kami menolak skenario seperti itu, tetapi saya akan mengatakan lebih banyak tentang ini di sini.

Perangkap

Dan di sinilah kita, dihantam oleh buku referensi dan rumus matematika, namun demikian terinspirasi oleh hasil yang diperoleh (ya apa yang ada - oleh fakta grafik yang indah!), Kami membuat pertemuan terakhir di depan pertahanan. Dan kita dihadapkan dengan babak baru perincian penting ...

N.p. 2 : Baik, baik, jelas ada kemenangan. Mereka yakin bahwa sudah ada semacam basis perangkat keras. Bagaimana dengan penargetan? Anda mungkin pernah mendengar tentang sistem PAT ( P ointing, A cquisition, dan T racking).

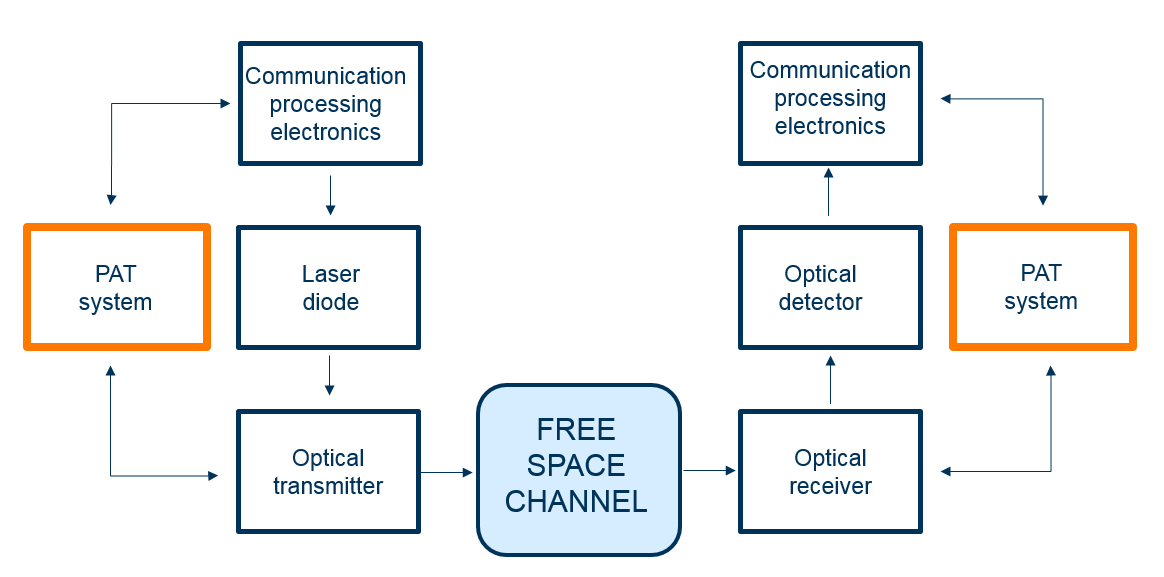
Fig. 6. Diagram sederhana dari sistem transceiver optik nirkabel.

N.p. 2 : Ya, ada beberapa contoh saluran optik untuk satelit besar [4] , namun, dalam hal ini Anda dapat membeli diameter penerima yang lebih besar, sudut divergensi laser yang lebih besar, dan daya transmisi yang lebih tinggi. Selain itu, CubeSat sendiri, saya pikir, bergetar sangat banyak ketika bergerak . Untuk saluran radio pada frekuensi yang relatif rendah, ini mungkin tidak penting, untuk optik - Anda sendiri mengerti. Apakah ada sistem stabilisasi dan PAT yang tepat saat ini?

Dan kami sangat bijaksana ...

N.p. 2 : Untuk itulah, untuk bagian saya, saya memberi Anda penilaian positif. Namun, saran saya untuk Anda: turun dari surga ke bumi ...

Dan kami, sangat kelelahan, jatuh: kami memutuskan untuk tidak melanjutkan proyek dengan optik satelit. Selain itu, bahkan selama pertemuan kami yang sering kami kumpulkan ...

Namun, tidak, tidak, dan bahkan catatan harapan siswa akan masuk ke hati bahwa guru itu salah dalam skeptisismenya. Tidak, tidak, dan saya ingin menemukan konsep dalam pencapaian teknologi modern. Dan pandangannya naik ke atas ...

Sastra

Janson SW, Welle RP Program komunikasi dan sensor sensor optik NASA: pembaruan // Konferensi AIAA / USU ke-28 Tahunan tentang Satelit Kecil. - 2014 .-- S. 4-7.
Wolf, M., & Kreß, D. (2003). Transmisi inframerah nirkabel jarak pendek: buoget tautan dibandingkan dengan RF . Komunikasi nirkabel IEEE, 10 (2), 8-14.
https://www.nii.ac.jp/qis/first-quantum/forStudents/lecture/pdf/noise/chapter12.pdf
Smutny B. et al. 5.6 Gbps tautan komunikasi intersatellite optik // Teknologi Komunikasi Laser Ruang-Bebas XXI. - Masyarakat Internasional untuk Optik dan Photonics, 2009.- T. 7199. - S. 719906.

Tapi bukankah kita melambaikan komunikasi optik? Laser, luar angkasa, CubeSat