Halo pembaca yang budiman! Saya mempersembahkan untuk Anda terjemahan dari bahasa Inggris artikel “Fisika, Perbatasan Selanjutnya” oleh Chris Hecker.

Saya, seorang pengembang Java pemula, dihadapkan dengan fakta bahwa bahan untuk membuat mesin dalam game fisik disajikan hanya dalam bahasa Inggris, oleh karena itu artikel ini diterjemahkan. Akan ada tiga artikel lagi dalam seri ini, saya akan mempostingnya sesegera mungkin. Selamat membaca!

Batas baru dalam fisika

Tidak ada keraguan bahwa setiap tahun grafik dalam game menjadi lebih realistis. Sudah hari ini, semua orang menciptakan (atau setidaknya menunjukkan tangkapan layar) dunia 3D dengan peta tekstur, dan ketika cukup banyak pekerja keras berkumpul untuk mengerjakan satu proyek, setiap pengembang dapat menggambar miliaran poligon tekstur realistis dan bayangan per detik. Dalam istilah teknis, apa yang masih harus dilakukan untuk membuat game di level tinggi? Akankah setiap pengembang dengan salinan buku "Belajar Menggunakan Perangkat Keras 3D dalam 21 Hari" dapat membuat game yang benar-benar mengesankan?

Tidak semuanya. Pengembang kelas atas akan terus meningkatkan standar dalam berbagai teknologi (seperti kompleksitas GUI, kecerdasan buatan, dan jaringan). Tentu saja, semua ini sangat penting, kami bahkan tidak dapat membahasnya dengan serius tanpa menentukan detail. Namun demikian, ada satu teknologi yang berlaku untuk semuanya, yang, menurut saya, akan menjadi faktor penentu dalam waktu dekat: fisika.

Pertimbangkan contoh berikut: apakah Anda ingat roda pemutar besar ini di salah satu level awal Duke Nukem 3D?



Gambar 1. Screenshot dari game "Duke Nukem 3D"

Bayangkan saja rotasi mereka akan dijelaskan bukan oleh animasi siklik, tetapi oleh mesin fisik nyata. Tiba-tiba, roda gigi menjadi sesuatu yang lebih dari sekadar hiasan permainan, seperti halnya salah satu dari mereka menyimpang dari sudut tertentu, dan berguling-guling di koridor di belakang Anda, seperti dalam film-film Indiana Jones. Atau bayangkan bahwa setelah menembakkan peralatan dari peluncur roket, itu akan bergulir di koridor dan menghancurkan teman Anda, yang merayap di belakang untuk membunuhmu! Mesin fisik membuat situasi seperti itu nyata.

Simulasi fisik adalah apa yang membuat dunia game utuh: berkat itu, "di sini" terletak di sini, jika Anda mengerti apa yang saya maksud. Setiap keajaiban dalam grafik di dunia tidak akan memungkinkan pemain untuk terjun ke dalam proses permainan jika dia akan melakukan penetrasi ke dalam pemain lain, atau ke dinding level, atau jika massa dan momen massa tidak dirasakan. Para animator di Disney menemukan perasaan massa ini sebagai apa yang memisahkan animasi yang baik dari animasi yang buruk. Menurut buku epik Disney Animation: The Illusion of Life oleh Frank Thomas dan Ollie Johnston, animator Disney, bahkan hanya menggantung poster di studio, harus selalu bertanya pada diri sendiri: "Apakah ada banyak bobot, kedalaman, dan keseimbangan dalam gambar mereka?" ? "

Tetapi hari ini hampir setiap permainan memiliki mesin fisika, bukan? Tidak diragukan lagi, inilah yang membuat mobil Anda tidak jatuh di ujung dunia permainan, berkat itu karakter Anda tidak terbang ke luar angkasa ketika mereka melompat, dan ini melemparkan perahu Anda ke samping ketika sebuah roket meledak di dekatnya. Namun, sebagian besar mesin fisik dalam game modern cukup lemah. Mereka hanya mengatasi tugas menjaga mobil agar tidak jatuh ke ujung dunia, tetapi kemampuan mereka tidak cukup untuk membawa permainan ke tingkat yang baru - di mana puing-puing mobil yang hancur dapat meledak tepat di trek, menyebabkan gulungan dinding dan mobil lain.

Efek fisik lain yang sering diabaikan termasuk: dari efek memutar sederhana akibat serangan singgung, hingga karakter dalam permainan itu sendiri menjaga keseimbangan dan bergerak mereka, tidak seperti yang animasi statis. Saya percaya bahwa banyak pengembang mengabaikan kemungkinan ini karena mereka tidak memahami matematika yang menggambarkan fisika, atau terlalu sibuk membuat peta tekstur untuk mempelajarinya. Serangan perangkat keras untuk bekerja dengan 3D akan menangani yang terakhir, dan saya memulai serangkaian artikel baru. Artikel pertama akan membahas formalitas. Pada akhir siklus kami, Anda sendiri dapat membuat mesin fisik yang akan membuat pemain merasa benar-benar tenggelam dalam permainan, berkat realisme yang luar biasa, atau surealis yang menghibur tetapi gigih.

Peringatan! Fisika = matematika, untuk menyelesaikan proyek yang menarik, Anda harus menggunakan keduanya. Sebelum ini membuat Anda takut, izinkan saya perhatikan bahwa matematika yang menggambarkan fisika tidak hanya elegan dan indah, tetapi juga memiliki karakter yang diterapkan. Artinya, itu bukan matematika abstrak untuk matematika. Setiap persamaan yang kita gunakan memiliki arti fisik yang nyata. Kami membuat persamaan dari model fisik, dan sebagai imbalannya persamaan memberi tahu kami bagaimana model berperilaku dalam waktu.

Perusahaan besar

Fisika adalah bidang ilmiah yang luas. Tetapi kami benar-benar tertarik pada bagian kecilnya yang disebut "dinamika", atau lebih tepatnya, "dinamika benda padat". Dinamika dapat didefinisikan dalam istilah bagian terkait - kinematika (doktrin pergerakan dalam waktu). Kinematika tidak fokus pada apa yang menyebabkan gerakan atau bagaimana tubuh berakhir di tempat mereka berada, itu hanya menggambarkan gerakan. Dinamika, sebaliknya, menggambarkan kekuatan dan massa yang berkontribusi pada nilai-nilai dari kinematika berubah seiring waktu. Seberapa jauh bola bisbol akan terbang jika waktu terbang 10 detik dan kecepatan awalnya 50 kilometer / jam, dan lintasannya adalah garis lurus - ini adalah masalah kinematik; seberapa jauh bola bisbol akan terbang di medan gravitasi bumi, jika saya memukulnya dengan kelelawar - ini adalah masalah yang dinamis.

Bagian dari dinamika yang menggambarkan padatan berhubungan dengan kendala yang kita tambahkan untuk objek yang disimulasikan. Bentuk tubuh padat tidak berubah selama simulasi - tubuh lebih cenderung kayu atau logam daripada seperti jeli. Kita dapat membuat angka yang diartikulasikan, misalnya, dari seseorang, dengan membangun setiap bagian dari tubuh yang solid dan membuat ligamen di antara mereka, tetapi kami tidak akan mengandalkan tulang yang tertekuk di bawah tekanan atau efek serupa. Ini akan memungkinkan kami untuk menyederhanakan persamaan kami tanpa kehilangan kualitas perilaku dinamis tubuh yang menarik.

Meskipun kita akan mempertimbangkan bagian kecil dari dinamika itu, dinamika tubuh yang kaku akan membutuhkan serangkaian artikel untuk menjelaskan esensinya. Kami memulai perjalanan kami dengan mempelajari dasar-dasar pemrograman komputer untuk menggambarkan gerakan benda kaku pesawat di bawah aksi pasukan. Saya terus-menerus mengulangi "pemrograman komputer", karena selain persamaan yang kami tulis untuk kinematika dan dinamika, kami juga akan belajar bagaimana menyelesaikan persamaan ini menggunakan perhitungan dengan angka floating point, yang sangat penting untuk diketahui oleh setiap programmer. Saya katakan "flat solid" karena kita hanya akan berurusan dengan dunia dua dimensi sepanjang artikel berikutnya dan seterusnya. Prinsip - dan pada kenyataannya lebih dari sekadar persamaan - juga dapat ditransfer ke dunia tiga dimensi, tetapi jelas semuanya jauh lebih sederhana di dunia dua dimensi, jadi kami akan belajar di sana sampai kami merasa yakin untuk memasuki ruang tiga dimensi. Dalam artikel mendatang, kita akan belajar untuk menggambarkan efek rotasi, pemrosesan kontak tubuh, dan, tentu saja, bagaimana melakukan semua ini di dunia tiga dimensi. Cukup kata-kata! Ayo mulai!

Bekerja dengan turunan

Ini mungkin mengejutkan Anda, tetapi Anda benar-benar tidak dapat memindahkan objek hanya dengan mendorongnya. Saya tahu, Anda pikir saya salah dalam membuktikan kebalikan dari saya dengan melemparkan majalah ini ke tempat sampah karena menulis omong kosong seperti itu, tetapi itu benar! Hanya menekan majalah tidak akan pernah secara langsung memengaruhi posisinya di ruang angkasa. Faktanya, tekanan bahkan tidak secara langsung mempengaruhi kecepatannya. Apa yang benar-benar mempengaruhi tekanan adalah percepatan jurnal, dan pada kenyataannya itu adalah salah satu kesimpulan paling penting dalam sejarah sains.

Untuk menggunakan fakta ini untuk melakukan sesuatu yang menarik, pertama-tama kita perlu berbicara tentang hubungan posisi tubuh dengan kecepatan dan akselerasi. Faktanya, semua nilai ini sangat terkait erat (seperti yang mungkin Anda ketahui): kecepatan adalah indikator perubahan dalam koordinat tubuh dari waktu ke waktu, dan akselerasi adalah indikator perubahan dalam kecepatan. Alat utama untuk mempelajari perubahan dalam jumlah ini dari waktu ke waktu adalah kalkulus diferensial. Jika Anda memahami hal ini, maka kami akan melanjutkan. Saya kira Anda pandai matematika. Kami hanya akan menggunakan perhitungan skalar dan vektor sederhana (turunan dan integral), tetapi itu tidak akan berlebihan jika Anda terbiasa dengan matematika secara keseluruhan. Untuk referensi: buku favorit saya tentang komputasi adalah Kalkulus dengan Analytic Geometry oleh Thomas and Finney.

Koordinat, kecepatan, dan akselerasi adalah kinematika yang akan dibahas dalam artikel ini. Lokasi benda padat dalam dunia dua dimensi, jelas, adalah sepasang koordinat X dan Y, yang menunjukkan koordinat ruang dari beberapa titik tubuh tertentu. Derivatif untuk vektor koordinat adalah vektor kecepatan, dan ini menunjukkan kepada kita ke arah mana titik bergerak (dan tubuh, jika kita mengabaikan rotasi, yang terjadi sekarang) dan seberapa cepat bergerak. Vektor kalkulus hanyalah kalkulus skalar dari setiap elemen vektor, sehingga turunan dari koordinat X adalah kecepatan tubuh sehubungan dengan X, dan seterusnya. Kami memperkenalkan notasi berikut. Biarkan koordinat tubuh menjadi vektor r, dan kecepatannya menjadi vektor v atau vektor r dengan bilangan prima. Kami mendapatkan persamaan:

$$

$${{dx} \ over {dt}} = v = r '$$

Persamaan 1

Jika kita membedakan vektor kecepatan dengan waktu, ini akan menunjukkan bagaimana vektor koordinat berubah seiring waktu. Akselerasi ditentukan oleh analogi. Ini adalah turunan pertama dari kecepatan atau turunan kedua dari vektor koordinat:

$$

$${{d ^ 2 r} \ over {dt ^ 2}} = r '' = {{dr '} \ over {dt}} = {{dv} \ over {dt}} = v' = a$$

Persamaan 2

Integral dari akselerasi akan memberi kita kecepatan, dan mengintegrasikan akselerasi dua kali, kita mendapatkan koordinat.

Hubungan-hubungan dalam kinematika ini menunjukkan bahwa kita dapat menemukan percepatan suatu objek, kita dapat mengintegrasikannya dari waktu ke waktu untuk mendapatkan kecepatan dan koordinat. Seperti yang akan kita lihat nanti, kita akan beralih ke integrasi berkali-kali dalam kode simulasi kita dan akan menghitung posisi baru untuk solid kita untuk setiap frame. Animasi Hore!

Berikut adalah contoh sederhana untuk dunia satu dimensi yang secara analitik dapat kita integrasikan. Mari kita sepakat bahwa kita ingin menemukan perubahan koordinat dari akhir frame terakhir ke waktu frame saat ini untuk menggambar posisi saat ini. Selanjutnya, kita katakan bahwa akselerasi solid kita sama dengan 5 unit acak / detik ^ 2. Kami akan menggunakan waktu yang telah berlalu dari akhir frame terakhir sebagai variabel t (dalam elemen integrasi dt).

$$

$$v (t) = ∫adt = ∫5dt = 5t + C$$

Persamaan 3

Persamaan di atas menunjukkan bahwa kecepatan adalah fungsi dari waktu yang berlalu dari frame terakhir. Kami menemukan konstanta integrasi, C, yang sama dengan kecepatan awal pada awal periode integrasi (pada t = 0).

$$

$$v (0) = 5 (0) + C$$

$$

$$v_0 = {C}$$

Persamaan 4

$$

$$v (t) = 5t + v_0 {}$$

Sekarang kita mengintegrasikan persamaan kecepatan kita untuk menemukan koordinat (sekali lagi, jangan lupa tentang konstanta integrasi):

$$

$$r (t) = ∫v (t) dt = ∫5t + v_0 dt = {{5} \ over {2}} t ^ 2 + v_0 t + r_0$$

Persamaan 5

Berdasarkan Persamaan 5, kita dapat menemukan posisi saat ini hanya dengan akselerasi yang diberikan jika kita mengetahui koordinat awal dan kecepatan (yang akan kita ambil dari frame terakhir) dan waktu yang telah berlalu. Variabel input adalah waktu, dan nilai fungsi adalah posisi saat ini. Kami juga akan menunjukkan waktu dalam Persamaan 4 untuk menghitung kecepatan akhir sehingga kami dapat menggunakan ini sebagai kondisi awal untuk frame berikutnya.

Semoga kekuatan bersamamu

Sekarang kita memiliki kesadaran bahwa kita perlu mengatur akselerasi dengan benar untuk mengintegrasikan persamaan kinematika untuk mendapatkan animasi. Output dari speaker di atas panggung. Ingat, seperti yang saya katakan, dengan menekan sesuatu, Anda secara langsung hanya memengaruhi akselerasi tubuh? Nah, "memberikan tekanan" hanyalah eufemisme untuk frasa "berlaku kekuatan" - salah satu dari dua variabel kunci dalam dinamika - dan sekarang kita dapat beralih ke Newton untuk mencari tahu bagaimana gaya mempengaruhi akselerasi. Hukum kedua Newton menghubungkan gaya F dengan turunan massa - besaran kedua dinamika - kali kecepatan. Produk massa dan kecepatan disebut "momentum tubuh", dilambangkan dengan p:

$$

$$F = p '= {{dp} \ over {dt}} = {{d (mv)} \ over {dt}} = mv' = ma$$

Persamaan 6

Massa adalah konstan untuk kecepatan yang sedang kita kerjakan sekarang, ini mengikuti dari turunannya dalam Persamaan 6, dan kita mendapatkan persamaan terkenal F = ma (walaupun saya yakin bahwa Newton pada awalnya menentukan gaya melalui turunan dari momentum).

Jika kita hanya berurusan dengan poin material, Persamaan 6 adalah yang kita butuhkan dalam dinamika. Untuk gaya tertentu dari titik material tertentu, akselerasi ditemukan dengan membagi gaya dengan massa. Ini memberi kita akselerasi, yang akan membantu menyelesaikan persamaan gerak dari contoh di atas. Namun demikian, kita berurusan dengan padatan dengan massa yang didistribusikan di area tertentu (volume, ketika datang ke dunia tiga dimensi), jadi kita masih perlu bekerja.

Pertama, pertimbangkan solid sebagai kumpulan massa titik. Kami akan menentukan momentum total, pT, untuk solid, sebagai jumlah momen dari semua poin yang membentuk tubuh (saya menggunakan pengindeksan atas, karena saya ingin menunjukkan dengan lebih jelas apa nilai kuantitatif yang dimiliki oleh poin-poin ini):

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

Persamaan 7

Kita dapat sangat menyederhanakan analisis dinamika benda tegar dengan memperkenalkan konsep pusat massa (CM). Vektor yang diarahkan ke pusat massa adalah jumlah linier vektor yang diarahkan dari semua titik massa benda padat dibagi dengan massa seluruh tubuh, M:

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \ lebih dari {M}}$$

Persamaan 8

Dengan menggunakan definisi pusat massa, kita dapat menyederhanakan Persamaan 7 dengan mengalikan kedua sisi dari Persamaan 8 dengan M, membedakannya, dan kemudian mengganti hasilnya dalam Persamaan 7:

$$

$${{d (Mr ^ {CM})} \ over {dt}} = {\ sum_ {i} {} {{d (m ^ ir ^ i) \ over dt}}} = {\ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

Persamaan 9

Sisi kanan dari Persamaan 9 adalah momentum total sebagaimana didefinisikan dalam Persamaan 7. Sekarang mari kita lihat sisi kiri persamaan: ini adalah kecepatan di pusat massa kali massa seluruh tubuh. Pindahkan sisi kanan ke kiri dan dapatkan:

$$

$$p ^ T = {{d (Mr ^ {CM})} \ over {dt}} = Mv ^ {CM}$$

Persamaan 10

Ini mengikuti dari Persamaan 10 bahwa momentum linear sama dengan total massa kali kecepatan diarahkan dari pusat massa, sehingga tidak perlu dijumlahkan dalam Persamaan 7 untuk menemukan momentum jika kita mengetahui massa tubuh dan arah vektor kecepatan dari pusat massa. Selanjutnya, semua hasil akhir dari perhitungan adalah menemukan integral untuk seluruh tubuh, tetapi pusat massa ada dan sangat menyederhanakan penentuan momentum total dari Persamaan 10, jadi kita tidak bisa khawatir - untuk menemukan momentum linier kita dapat menganggap tubuh sebagai titik material dengan kecepatan dan massa yang diberikan.

Dengan analogi, gaya total adalah turunan dari momentum total, sehingga konsep pusat massa dapat digunakan untuk menyederhanakan persamaan gaya:

$$

$$F ^ T = p ^ T = Mv '^ {CM} = Ma ^ {CM}$$

Persamaan 11

Singkatnya, ini mengikuti dari Persamaan 11 bahwa kita dapat mempertimbangkan semua gaya yang berinteraksi dengan padatan, seolah-olah vektor penjumlahannya memiliki efek pada titik pusat massa, yang berisi massa seluruh tubuh. Kami membagi gaya (baca gravitasi) dengan M untuk menemukan percepatan pusat massa, dan kemudian mengintegrasikan percepatan dalam waktu untuk mendapatkan kecepatan dan koordinat tubuh. Karena kita mengabaikan efek rotasi sampai artikel berikutnya, kita sudah memiliki semua persamaan yang kita butuhkan untuk menggambarkan dinamika tubuh yang kaku. Perhatikan bahwa Persamaan 11 tidak mengandung informasi tentang di mana gaya yang diterapkan pada benda diarahkan. Ini akan muncul ketika kita berurusan dengan momentum linear dan pusat massa, dan kita hanya menerapkan kekuatan pada CM untuk menemukan percepatan pusat massa. Ketika kita menghitung rotasi benda di bawah pengaruh gaya-gaya ini di artikel selanjutnya, kita akan melihat bagaimana koordinat penerapan gaya digunakan.

Ode to Joy

Pada tahap ini, kita dapat mempertimbangkan contoh lain integrasi analitik, menggunakan Persamaan 11 untuk menemukan percepatan pusat massa alih-alih nilai yang dipilih secara sewenang-wenang = 5. Namun demikian, kita menghadapi masalah serius, karena integrasi analitis biasanya tidak memiliki nilai yang diterapkan, karena itu terlalu rumit, jadi kami akan fokus pada apa yang disebut integrasi numerik persamaan diferensial biasa (ODE). Wow, sekarang kedengarannya seperti matematika sungguhan! Setelah Anda mempelajari ini, sekarang saatnya untuk meningkatkan standar. Untungnya, integrasi numerik ODE tidak sesulit kelihatannya pada pandangan pertama! Untuk memahami apa artinya ini, kita beralih dari kata ke tindakan!

Jadi, persamaan diferensial adalah persamaan yang berisi turunan dari jumlah dependen selain fungsi itu sendiri, variabel dan parameter independen. Ini verbose, tetapi di sini adalah contoh untuk gaya yang bervariasi-waktu dalam dunia satu dimensi: F = 2t, F adalah kuantitas dependen, dan t adalah kuantitas independen. Nilai F ditentukan hanya oleh F. Biarkan persamaan gaya hanya bergantung pada kecepatan tubuh kita.Kekuatan hambatan udara meningkat dengan meningkatnya kecepatan pesawat. Mari kita kembali ke contoh di dunia satu dimensi, bagaimana jika F = -v berarti gaya gesek memperlambat tubuh kita sebanding dengan kecepatan? Kami memiliki masalah, karena kami menyelesaikan persamaan sebagai berikut: F = ma = -v dan, membaginya dengan m, kami dapatkan (ingat bahwa akselerasi adalah turunan dari kecepatan):

$$

$$a = {{dv}\over {dt}} = {-v\over m}$$

Persamaan 12 Persamaan

diferensial ini, (persamaan kecepatan mengandung turunan kecepatan dalam Persamaan 12) disebut persamaan diferensial biasa, karena hanya berisi turunan biasa dari kuantitas dependen (sebagai lawan dari derivatif parsial, yang membentuk persamaan diferensial parsial [PDE], yang tidak kita miliki kita akan bicara).

Sekarang mari kita beralih ke bagian selanjutnya dari frase kita: integrasi. Bagaimana kita sebelumnya mengintegrasikan dv / dt untuk menemukan v dalam kondisi persamaan ini?

Ini akan tampak sulit dipercaya, tetapi hampir setiap persamaan dalam fisika adalah diferensial, sehingga ODE telah dipelajari dengan baik. Persamaan diferensial sering kali dapat ditemukan dalam fisika, karena sering kali laju perubahan kuantitas kuantitatif tergantung pada kuantitas itu sendiri. Sebagai contoh, kita telah mencatat bahwa pengereman (besarnya perubahan kecepatan), termasuk kecepatan hambatan udara, tergantung pada kecepatan. Contoh lain dari fisika: pendinginan (laju kehilangan panas tergantung pada suhu saat ini) dan peluruhan radioaktif (laju peluruhan tergantung pada seberapa banyak bahan radioaktif hadir).

Kata terakhir dalam frasa kita - numerik - adalah keselamatan kita. Saya mengatakan ini karena teori integrasi analitik persamaan diferensial, bahkan yang paling sederhana, sangat besar dan agak membingungkan. Meskipun, ironisnya, integrasi ODE menggunakan metode numerik komputer sebenarnya relatif mudah dipahami. Selanjutnya, saya akan menjelaskan integrator numerik sederhana berdasarkan metode Euler, dan akan memperbaikinya di artikel berikutnya.

Hampir semua integrator numerik, tetapi tidak ada yang se eksplisit metode Euler, hanya didasarkan pada definisi lama komputasi melalui turunan pertama dari slant: dy / dx menentukan kemiringan y tergantung pada x. Sebagai contoh, jika kita memiliki persamaan linear y = 5x, maka dy / dx = 5 berarti bahwa kemiringan adalah konstanta sama dengan 5 untuk setiap x, dan, seperti yang dapat Anda asumsikan, ini adalah garis lurus. Contoh yang sedikit lebih sulit adalah parabola y = x2. Dalam hal ini, dy / dx = 2x, dan ini adalah fungsi untuk menentukan kemiringan baru untuk setiap koordinat x. Saya menggambarkan y = x2 pada Gambar 2: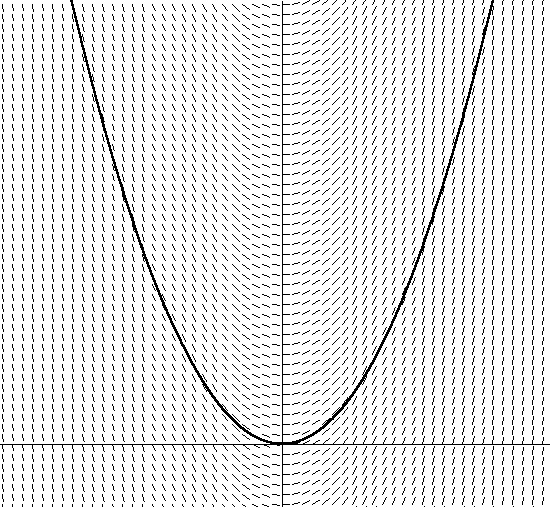



Gambar 2. y = x2

Selain itu, saya juga menetas arah vektor miring dengan menyelesaikan persamaan dy / dx = 2x + C untuk semua x. Perhatikan fakta bahwa sudut vektor cenderung sama dengan garis singgung dari sudut garis singgung pada titik ini. Perhatikan juga bahwa ada banyak parabola berbeda yang memenuhi sudut himpunan garis singgung, hanya berbeda dalam pergeseran sepanjang sumbu y. Masing-masing parabola ini diperoleh dengan menggunakan konstanta integrasi yang berbeda, yang terkandung dalam persamaan dy / dx = 2x + C. Parabola yang saya bayangkan memiliki konstanta integrasi 0. Jika saya memilih konstanta lain, misalnya 1, saya mendapatkan persamaan y = 2x + 1. Ini berarti ada parabola yang serupa dengan pergeseran 1 unit ke sumbu y.

Sekarang pikirkan tentang fakta bahwa jika Anda tidak tahu bidang vektor pada Gambar 2 yang didefinisikan oleh parabola, maka cukup duduk dalam genangan air. Jadi, jika Anda ingin menyelesaikan persamaan tangen, Anda hanya perlu mengikuti arah vektor di setiap titik, mengubah arah sesuai dengan perubahan arah bidang vektor. Anda akan terkejut bahwa setelah beberapa waktu, Anda akan melihat bahwa Anda bergerak di sepanjang lintasan parabola (atau sepanjang bagian parabola), tergantung di mana Anda mulai. Tanpa disadari, Anda mengintegrasikan persamaan bidang vektor. Anda menemukan parabola tertentu (tergantung di mana Anda memulai, atau pada kondisi awal), hanya menggunakan persamaan turunan (menghitung dy / dx saat Anda bergerak di bidang vektor).

Melakukan hal yang sama untuk persamaan diferensial nyata juga sederhana. Untuk persamaan diferensial dari tipe dy / dx = f (x, y), menemukan turunan dy / dx sebagai garis singgung ke f (x, y) menggambarkan sudut kemiringan tangen untuk setiap koordinat pada grafik x, y. Jika Anda merencanakan bidang vektor yang diberikan oleh dy / dx = f (x, y), Anda dapat mengikuti ini dengan analogi dengan parabola dengan menemukan turunan pada setiap titik dan mengikuti ke arah itu. Gambar 2 menunjukkan bidang vektor untuk Persamaan 12, persamaan kami untuk hambatan udara, dengan kecepatan di sepanjang sumbu vertikal dan waktu di sepanjang horizontal (saya sewenang-wenang memilih m = 1 untuk grafik ini).



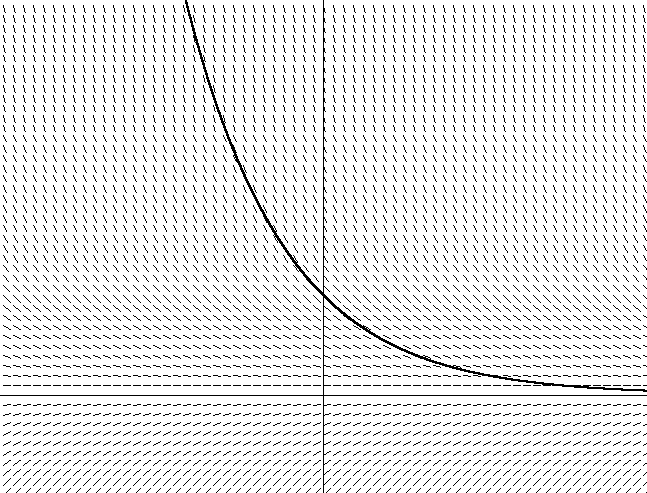Gambar 3. dv / dt = -v / m

Itu juga menunjukkan salah satu dari banyak kurva yang mungkin. Anda mungkin memperhatikan bahwa jika Anda memilih posisi awal dalam grafik (yang tergantung pada kecepatan awal dalam persamaan), seiring waktu, kecepatan akan cenderung ke nol, karena gaya gesek memperlambat tubuh. Anda juga dapat melihat bagaimana penurunan kecepatan tergantung pada nilai kecepatan saat ini - semakin cepat Anda bergerak, semakin cepat berkurang. Ini menjadi jelas ketika yang sama mengikuti dari Persamaan 12.

Integrasi numerik mirip dengan apa yang kami lakukan pada bagan. Algoritma Euler untuk integrasi numerik cukup mengikuti bidang vektor sesuai dengan posisi awal dengan menemukan turunan dari persamaan (-v / m untuk contoh kita dengan gaya gesek) untuk menentukan kemiringan pada titik saat ini, dan kemudian hanya bergerak maju langkah demi langkah dalam waktu, tergantung pada nilai h tidak berubah, di sepanjang lereng. Kemudian posisi baru dihitung untuk menentukan kemiringan baru setelah interval waktu tertentu:

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

Atau lebih tepatnya untuk persamaan hambatan udara kami:

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

Jelas, metode Euler memberikan kesalahan kecil dengan setiap langkah waktu, karena vektor kecepatan nyata (dan karenanya kurva solusi) membungkuk dengan penyimpangan di setiap titik, dan algoritma Euler sedikit menyimpang dari sudut kemiringan. Tetapi jika langkah waktu, h adalah jumlah yang agak kecil, kesalahan cenderung nol. Kami akan membahas ini secara lebih rinci di masa depan.

Ini semua yang perlu Anda ketahui tentang integrasi numerik menggunakan metode Euler. Anda mungkin bertanya bagaimana kami akan mengintegrasikan kecepatan untuk mendapatkan koordinat. Kami cukup menggunakan metode Euler lagi untuk mengintegrasikan dr / dt = v, sama seperti kami mengintegrasikan dv / dt = a, dengan analogi. Kami mendapatkan dua persamaan diferensial yang terhubung (satu lagi dari kemenangan kami):

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

Ini memberi kita algoritme alternatif untuk menghitung koordinat setelah tindakan gaya yang diterapkan secara sewenang-wenang pada objek kita (yang mungkin tergantung pada kecepatan, seperti yang kita lihat, atau waktu, atau bahkan posisi tubuh kita dan tubuh lain, atau semuanya sekaligus!). Untuk metode Euler, tidak masalah seperti apa gaya yang diberikan, karena Anda dapat menghitungnya kapan saja. Euler tertarik pada besarnya pengaruh kekuatan pada massa, seperti yang cenderung, dan hanya itu.
Saya kehabisan ruang, jadi saya tidak punya cara untuk menyediakan tautan. Lain kali saya akan menyarankan berbagai buku indah, dan kami akan mencari cara menghitung rotasi padatan.

Dan meskipun tubuhnya tidak sekokoh yang kita inginkan, Chris Hecker memiliki kepribadian yang dinamis. Jika Anda menerapkan kekuatan, dia akan menjawab email checker@bix.com.

Catatan penerjemah: permainan kata pun disajikan di sini, topik artikel dan isinya dimainkan.

PS Penulis terjemahan mengucapkan terima kasih khusus kepada para pengguna berez dan MarazmDed untuk pengeditan terjemahan mereka. Terima kasih