Pendahuluan
Kata bahasa Inggris wavelet (dari bahasa Prancis "ondelette") secara harfiah diterjemahkan sebagai "gelombang pendek (kecil)." Dalam berbagai terjemahan artikel asing ke dalam bahasa Rusia, ada juga istilah: “burst”, “burst function”, “low-wave function”, “wave”, dll.
Transformasi wavelet (VP) banyak digunakan untuk analisis sinyal. Selain itu, ia menemukan aplikasi hebat di bidang kompresi data. VP dari sinyal satu dimensi adalah perwakilannya dalam bentuk seri umum atau integral Fourier atas sistem fungsi basis.
psiab(t)= frac1 sqrta psi kiri( fract−ba kanan) , (1)
dibangun dari ibu (sumber) wavelet
psi(t) memiliki sifat-sifat tertentu karena operasi time shift (b) dan perubahan skala temporal (a).
Pengganda
1/ sqrta memastikan independensi norma fungsi (1) dari angka penskalaan (a). Untuk nilai yang diberikan dari parameter a dan b, fungsinya
psiab(t) dan ada wavelet yang dihasilkan oleh mother wavelet
psi(t) .
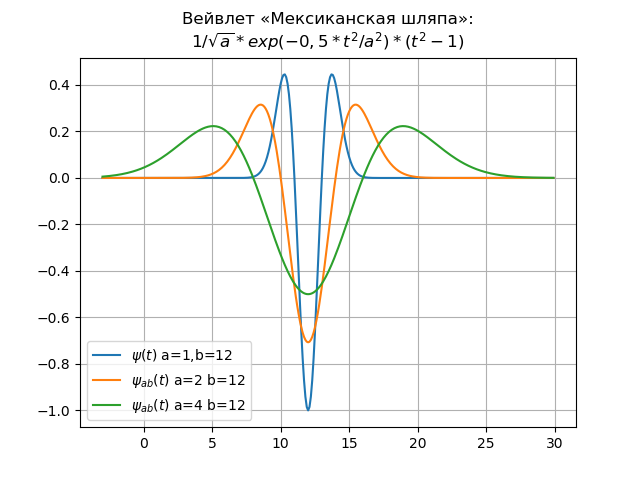
Contohnya adalah wavelet topi Meksiko dalam domain waktu dan frekuensi:
Daftar wavelet untuk domain waktufrom numpy import* import matplotlib.pyplot as plt x= arange(-4,30,0.01) def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f plt.title(" « »:\n$1/\sqrt{a}*exp(-0,5*t^{2}/a^{2})*(t^{2}-1)$") y=[w(1,12,t) for t in x] plt.plot(x,y,label="$\psi(t)$ a=1,b=12") y=[w(2,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=2 b=12") y=[w(4,12,t) for t in x] plt.plot(x,y,label="$\psi_{ab}(t)$ a=4 b=12") plt.legend(loc='best') plt.grid(True) plt.show()
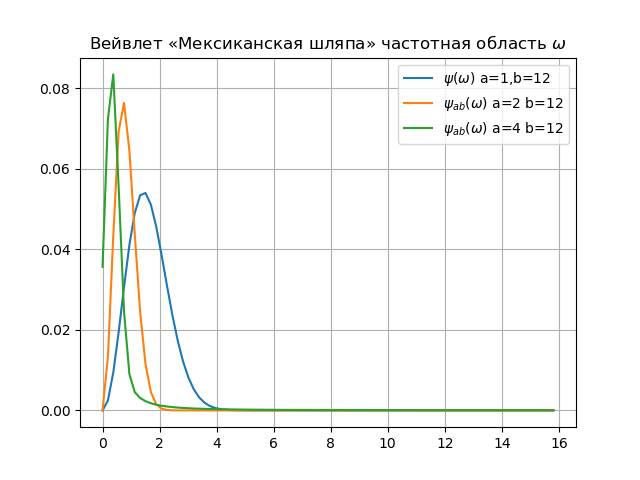
Daftar untuk spektrum wavelet from numpy import* from pylab import * from scipy import * import os def w(a,b,t): f =(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1) return f x= arange(-4,30,0.2) def plotSpectrum(y,Fs): n = len(y) k = arange(n) T = n/Fs frq = k/T frq = frq[range(int(n/2))] Y = fft(y)/n Y = Y[range(int(n/2))] return Y,frq xlabel('f (Hz)') ylabel('|Y(f)|') Fs=1024.0 y=[w(1,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi(\omega)$ a=1,b=12") y=[w(2,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=2 b=12") y=[w(4,12,t) for t in x] Y,frq=plotSpectrum(y,Fs) plot(frq,abs(Y),label="$\psi_{ab}(\omega)$ a=4 b=12") plt.title(" « » $\omega$") legend(loc='best') grid(True) show()
 Kesimpulan:
Kesimpulan:1. Antara konsep Fourier harmonik dan skala wavelet, benar-benar ada hubungan. Hal utama dalam hubungan ini adalah proporsi terbalik dari frekuensi dan skala alami. Selain itu, mengurangi skala, kami meningkatkan bandwidth dari spektrum wavelet.
2. Dengan mengubah skala (meningkatkan lead ke penyempitan spektrum fungsi Fourier
psiab(t) ), wavelet dapat mendeteksi perbedaan karakteristik pada skala yang berbeda (frekuensi), dan karena pergeseran, menganalisis sifat sinyal pada titik yang berbeda pada seluruh interval yang dipelajari. Oleh karena itu, ketika menganalisis sinyal non-stasioner, karena properti lokalitas wavelet, mereka mendapatkan keuntungan yang signifikan atas transformasi Fourier, yang hanya memberikan informasi global tentang frekuensi (skala) dari sinyal yang dianalisis, karena sistem fungsi yang digunakan (eksponen kompleks atau sinus dan kosinus) didefinisikan pada interval tak terbatas.
3. Daftar di atas yang ditulis dalam bahasa Python tingkat tinggi yang didistribusikan secara bebas memungkinkan Anda memilih fungsi untuk wavelet yang memenuhi persyaratan yang ditentukan. Namun, perlu juga memperhitungkan semua tanda-tanda utama dari wavelet.
Tanda-tanda utama wavelet
Keterbatasan. Kuadrat dari norma fungsi harus terbatas:
left | psi right |2= int infty− infty kiri| psi(t) right|2dt< infty . (2)
Lokalisasi VP, berbeda dengan transformasi Fourier, menggunakan fungsi awal lokal baik dalam waktu dan frekuensi. Untuk melakukan ini, cukup bahwa persyaratan terpenuhi:
kiri| psi(t) kanan| leqC(1+ kiri|t kanan|)−1− varepsilon dan
kiri|S psi( omega) kanan| leqC(1+ kiri| omega kanan|)−1− varepsilon di
varepsilon>0 , (3)
Misalnya, fungsi delta
delta(t) dan fungsi harmonik tidak memenuhi kondisi yang diperlukan untuk lokalisasi simultan dalam domain waktu dan frekuensi.
Rata-rata nol. Grafik fungsi asli harus berosilasi (bergantian) di sekitar nol pada sumbu waktu dan memiliki area nol:
int infty− infty psi(t)dt=0 . (4)
Dari kondisi ini, menjadi jelas pilihan nama "wavelet" - gelombang kecil.
Sama dengan area fungsi nol
psi(t) , yaitu momen nol, mengarah pada fakta bahwa Fourier berubah
S psi( omega) fungsi ini sama dengan nol untuk
omega=0 dan memiliki bentuk filter band-pass. Untuk berbagai nilai (a), ini akan menjadi seperangkat filter bandpass.
Seringkali untuk aplikasi perlu bahwa tidak hanya nol, tetapi semua n momen pertama sama dengan nol:
int infty− inftytn psi(t)dt=0 . (5)
Gelombang-ke-n memungkinkan seseorang untuk menganalisis struktur sinyal frekuensi tinggi yang lebih halus, menekan komponen-komponennya yang perlahan berubah.
Buatan sendiri Fitur karakteristik VP adalah kemiripan diri. Semua wavelet dari keluarga tertentu
psiab(t) memiliki jumlah osilasi yang sama dengan wavelet ibu
psi(t) , karena diperoleh darinya melalui transformasi skala (a) dan pergeseran (b).
Transformasi Wavelet Berkelanjutan
Transformasi wavelet kontinu (integral) (NVP atau WT - transformasi wavelet kontinu). Kami membangun dasar
psiab(t) menggunakan transformasi skala kontinu (a) dan transfer (b) dari wavelet ibu
psi(t) dengan nilai arbitrer dari parameter dasar a dan b dalam rumus (1).
Kemudian, menurut definisi, langsung (analisis) dan membalikkan (sintesis) NVP (yaitu, PNVP dan ONVP) dari sinyal S (t) ditulis sebagai berikut:
Ws(a,b)=(S(t), psiab(t))= frac1 sqrta int infty− inftyS(t) psi kiri( fractba kanan)dt , (6)
S(t)= frac1C psi int infty− infty int infty− inftyWs(a,b) psiab(t) fracdadba2 , (7)
dimana
C psi - koefisien normalisasi,
C psi= int infty− infty kiri| psi( omega) kanan|2 kiri| omega right|−1d omega< inftydi mana: (•, •) adalah produk skalar dari faktor yang sesuai,
mathbf psi( omega) - Transformasi Fourier dari wavelet
psi(t) . Untuk wavelet ortonormal
C psi=1 .
Ini mengikuti dari (6) bahwa spektrum wavelet
Ws(b,a) (spektrum wavelet, atau spektrum skala waktu), tidak seperti spektrum Fourier (spektrum tunggal), adalah fungsi dari dua argumen: argumen pertama a (skala waktu) mirip dengan periode osilasi, mis. terbalik dengan frekuensi, dan b –– kedua mirip dengan offset sinyal di sepanjang sumbu waktu.
Perlu dicatat bahwa
Ws(b,a0) mencirikan ketergantungan waktu (pada
a=a0) , sedangkan dependensi
Ws(a,b0) adalah mungkin untuk mencocokkan ketergantungan frekuensi (untuk
b=b0 )
Jika sinyal yang dipelajari S (t) adalah satu pulsa berdurasi tunggal
tauu terkonsentrasi di lingkungan
t=t0 , maka spektrum waveletnya akan memiliki nilai terbesar di sekitar titik dengan koordinat
a= tauu,b=t0 .
Metode presentasi Ws(b,a) mungkin berbeda. Spektrum
Ws(b,a) adalah permukaan dalam ruang tiga dimensi. Namun, seringkali alih-alih gambar permukaan, proyeksi ke bidang ab disajikan dengan tingkat iso (atau gambar berbagai warna), yang memungkinkan untuk melacak perubahan intensitas amplitudo EP pada skala yang berbeda (a) dan dalam waktu (b).
Selain itu, mereka menggambarkan garis-garis ekstrem lokal dari permukaan ini, yang disebut kerangka (skeleton), yang mengungkapkan struktur sinyal yang dianalisis.
Transformasi wavelet kontinu saat menentukan spektrum wavelet berdasarkan induk wavelet - “Topi Meksiko”.
Gelombang ibu lainnya yang digunakan untuk NVP juga digunakan:

Continuous VP banyak digunakan dalam pemrosesan sinyal. Secara khusus, analisis wavelet (VA) memberikan peluang unik untuk mengenali fitur dan fungsi sinyal (fungsi) lokal dan “halus”, yang penting di banyak bidang teknik radio, komunikasi, elektronik radio, geofisika, dan cabang ilmu pengetahuan dan teknologi lainnya. Mari kita pertimbangkan kemungkinan ini dengan beberapa contoh sederhana.
Osilasi harmonik.Sinyal memiliki bentuk:
s(t)=Asin( omegat− phi)dimana:
A=1V, omega= frac2 piT= frac2 pi50, psi=0Fungsi pembentukan wavelet:
MHAT(t):= fracd2dt2exp(−t2/2) ,
Wavelet:
psi(a,b,t)= frac1 sqrtaMHAT kiri( fract−ba kanan) ,
Spektrum wavelet: N: = 256, a: = 1..30, b: = 0..50,
W(a,b):= intN−N psi(a,b,t)s(t)dt,Nab:=W(a,b). .
Daftar program from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 T=50 def S(t): return sin(2*pi*t/T) plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,100,1)] x=[t for t in arange(0,100,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49,49) fig = plt.figure("- : ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
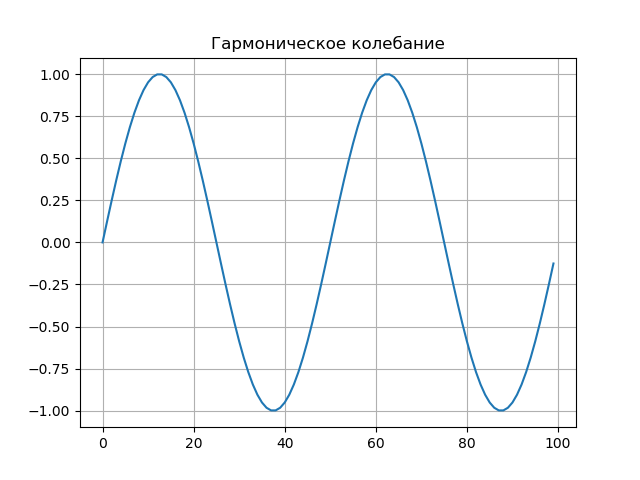
Grafik sinyal.

Grafik spektrum dua parameter
Nab=W(ab) ditampilkan sebagai permukaan dalam ruang tiga dimensi.

Perlu dicatat bahwa bagian W (a, b) untuk skala waktu
a=a0 mencirikan osilasi awal s (t). Selain itu, amplitudo maksimum di
a0:1/ omega . Ketergantungan
W(a0,b0) dapat cocok dengan spektrum osilasi saat ini di
b=b0 .
Jumlah dari dua osilasi harmonik.Sinyal memiliki bentuk:
s(t):=A1sin( omega1t)+A2sin( omega2t)dimana:
A1=A2=1V, omega1= frac2 piT1, omega2= frac2 piT2,T1=50s,T2=10s .
MHAT(t):= fracd2dt2 kiri[e−t2/2 kanan] , N: = 256,
psi(a,b,t):=MHAT kiri( fractba kanan),W(a,b):= intN−N psi(a,b,t)f(t)dt , a: = 1 ... 30, b: = 0 ... 50,
Nab:=W(a,b) .
Daftar program from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): return sin(2*pi*t/10)+sin(2*pi*t/50) plt.figure(' ') plt.title(' ', size=12) y=[S(t) for t in arange(0,250,1)] x=[t for t in arange(0,250,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,50,1) y = arange(1,50,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(49, 49) fig = plt.figure("-:2- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z, 100) plt.figure() q=[w(2,i) for i in y] p=[i for i in y] plt.plot(p,q,label='w(2,b)') q=[w(15,i) for i in y] plt.plot(p,q,label='w(15,b)') q=[w(30,i) for i in y] plt.plot(p,q,label='w(30,b)') plt.legend(loc='best') plt.grid(True) plt.figure() q=[w(i,13) for i in x] p=[i for i in x] plt.plot(p,q,label='w(a,13)') q=[w(i,17) for i in x] plt.plot(p,q,label='w(a,17)') plt.legend(loc='best') plt.grid(True) plt.show()

Grafik sinyal.
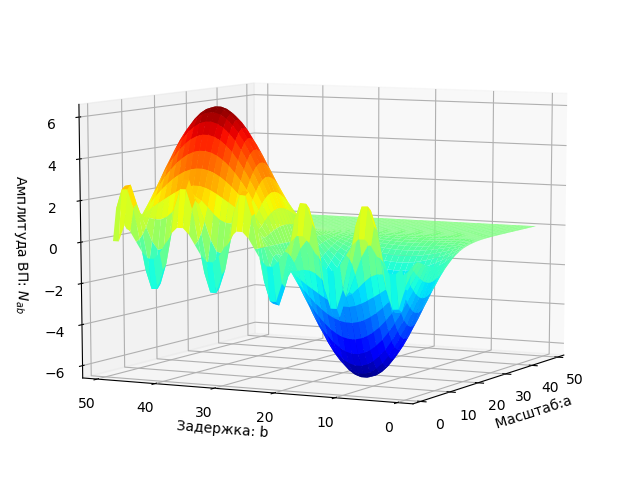
Plot spektrum dua-parameter W (a, b) ditampilkan sebagai permukaan dalam ruang tiga dimensi.
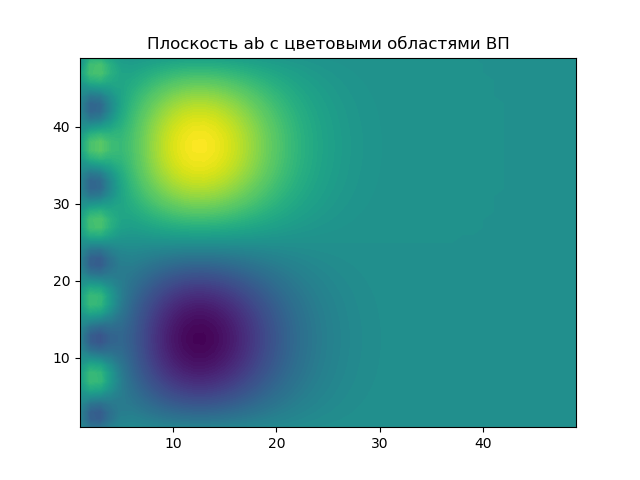
Bidang parameter a, b di mana hasil EP disorot dalam area berwarna.

Grafik menunjukkan “penampang” spektrum wavelet untuk dua nilai parameter a. Dengan parameter skala waktu yang relatif kecil a, untuk
a1=2(a1:1/ omega2) , penampang spektrum hanya membawa informasi tentang komponen frekuensi tinggi dari sinyal, menyaring (menekan) komponen frekuensi rendahnya.
Sebagai peningkatan, perluasan fungsi basis
psi( fract−ba) , oleh karena itu, mempersempit spektrumnya, dan mempersempit bandwidth dari "jendela" frekuensi. Hasilnya, kapan
a2=15(a2:1/ omega1) penampang spektrum hanya komponen frekuensi rendah dari sinyal.
Dengan peningkatan lebih lanjut dalam a, pita jendela masih menurun dan tingkat komponen frekuensi rendah ini menurun menjadi komponen konstan (untuk a> 25), yang sama dengan nol untuk sinyal yang dianalisis.

Grafik menunjukkan bagian-bagian dari spektrum wavelet W (a, b) karakterisasi
spektrum sinyal saat ini di
b1=13 dan
b2=17 . Spektrum sinyal yang dipertimbangkan, berbeda dengan harmonik, mengandung komponen frekuensi tinggi di wilayah nilai kecil skala waktu a (a: 1..3), yang sesuai dengan komponen kedua sinyal
A2sin( omega2t) .
Momentum persegi panjang.U:=5,t0:=20, tau:=60s(t):= beginvmatrixU,jikat0 leqt leqt0+ tau0,jikatidak endvmatrixMHAT(t):= fracd2dt2exp kiri( frac−t22 kanan)N:=128, psi(a,b,t):=MHAT kiri( fractba kanan),W(a,b):= intN−N psi(a,b,t)f(t)dta:=1..50,b:=0..100,Nba:=W(a,b)Daftar program from scipy.integrate import quad from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm N=256 def S(t): U=5;t0=20;tau=60 if t0<=t<=t0+tau: return U else: return 0 plt.figure() plt.title(' ', size=12) y=[S(t) for t in arange(0,120,1)] x=[t for t in arange(0,120,1)] plt.plot(x,y) plt.grid() def w(a,b): f = lambda t :(1/a**0.5)*exp(-0.5*((tb)/a)**2)* (((tb)/a)**2-1)*S(t) r= quad(f, -N, N) return round(r[0],3) x = arange(1,100,1) y = arange(1,100,1) z = array([w(i,j) for j in y for i in x]) X, Y = meshgrid(x, y) Z = z.reshape(99, 99) fig = plt.figure("3D- ") ax = Axes3D(fig) ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel(' :a') ax.set_ylabel(': b') ax.set_zlabel(' : $ N_{ab}$') plt.figure("2D- z = w (a,b)") plt.title(' ab ', size=12) plt.contourf(X, Y, Z,100) plt.show()
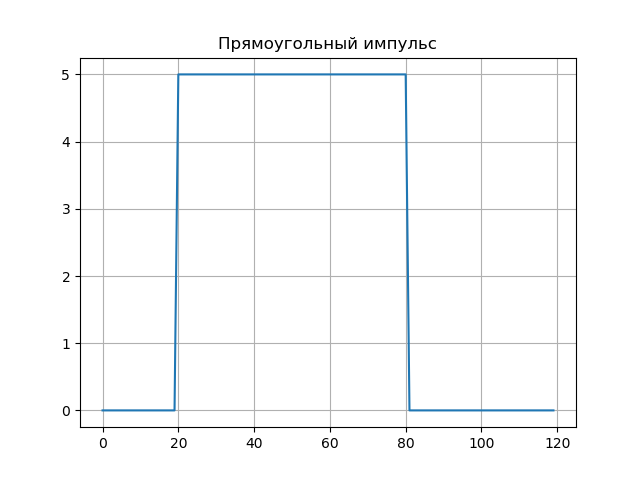


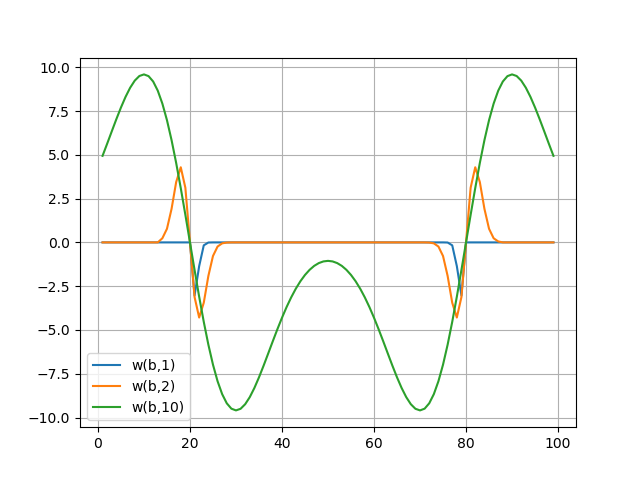
Spektrum wavelet diperlihatkan dalam grafik, spektrum wavelet dengan baik menyampaikan fitur halus dari sinyal - lompatannya pada sampel b = 20 dan b = 80 (untuk: 1.10).
Kesimpulan
Publikasi ini bersifat mendidik, memberikan informasi dasar tentang analisis wavelet secara umum, dan contoh-contoh sederhana dalam bahasa pemrograman tingkat tinggi yang didistribusikan secara bebas, Python menunjukkan fitur-fitur analisis wavelet berkelanjutan dengan grafik 3D dan visualisasi 2D yang luas.
PS Penulis tidak mengurangi keuntungan tanpa syarat dari analisis wavelet menggunakan Matlab baik dalam hal jumlah wavelet dan kecepatan. Namun dalam Python masih ada ruang untuk pengembangan lebih lanjut: scipy.signal dan PyWavelets.