Semua orang di industri TI tahu betapa sulitnya menilai batas waktu proyek. Sulit menilai secara objektif berapa lama waktu yang dibutuhkan untuk menyelesaikan tugas yang sulit. Salah satu teori favorit saya adalah ini hanya artefak statistik.

Misalkan Anda mengevaluasi proyek pada 1 minggu. Misalkan ada tiga hasil yang kemungkinan sama: baik itu akan memakan waktu 1/2 minggu, atau 1 minggu, atau 2 minggu. Hasil median sebenarnya sama dengan perkiraan: 1 minggu, tetapi nilai rata-rata (alias rata-rata, alias nilai yang diharapkan) adalah 7/6 = 1,17 minggu. Skor sebenarnya dikalibrasi (tidak memihak) untuk median (yaitu 1), tetapi tidak untuk rata-rata.

Model yang masuk akal untuk "faktor inflasi" (waktu aktual dibagi dengan perkiraan waktu) akan menjadi sesuatu seperti distribusi lognormal . Jika estimasi sama dengan satu minggu, maka kami mensimulasikan hasil nyata sebagai variabel acak yang didistribusikan sesuai dengan distribusi normal selama sekitar satu minggu. Dalam situasi seperti itu, median distribusi tepat satu minggu, tetapi nilai rata-rata jauh lebih besar:



Jika kita mengambil logaritma koefisien inflasi, kita mendapatkan distribusi normal sederhana dengan pusat sekitar 0. Ini mengasumsikan koefisien inflasi median 1x, dan, seperti yang Anda harapkan, ingat, log (1) = 0. Namun, dalam berbagai masalah mungkin ada ketidakpastian yang berbeda di sekitar 0. Kita dapat memodelkan mereka dengan mengubah parameter σ, yang sesuai dengan standar deviasi dari distribusi normal:



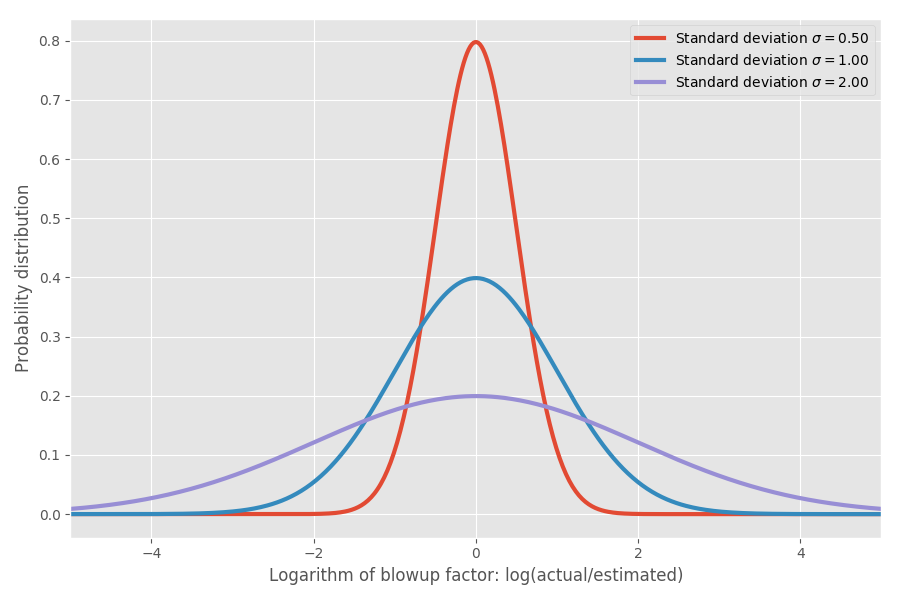
Hanya untuk menunjukkan bilangan real: ketika log (aktual / diperkirakan) = 1, maka koefisien inflasi exp (1) = e = 2.72. Kemungkinan besar proyek akan mencapai exp (2) = 7,4 kali, dan itu akan berakhir pada exp (-2) = 0,14, mis., 14% dari perkiraan waktu. Secara intuitif, alasan rata-rata begitu besar adalah karena tugas yang berjalan lebih cepat daripada yang diantisipasi tidak dapat mengimbangi tugas yang membutuhkan waktu lebih lama daripada yang diantisipasi. Kami terbatas pada 0, tetapi tidak terbatas pada arah lainnya.

Apakah ini hanya model? Aku berharap kamu bisa! Tetapi segera saya akan sampai ke data nyata dan pada beberapa data empiris saya akan menunjukkan bahwa sebenarnya cukup baik konsisten dengan kenyataan.

Memperkirakan Garis Waktu Pengembangan Perangkat Lunak

Sejauh ini, sangat bagus, tapi mari kita benar-benar mencoba memahami apa artinya ini dalam hal memperkirakan jadwal pengembangan perangkat lunak. Misalkan kita melihat rencana 20 proyek perangkat lunak yang berbeda dan mencoba untuk mengevaluasi berapa lama waktu yang dibutuhkan untuk menyelesaikan semuanya .

Di sinilah rata-rata menjadi menentukan. Rata-rata dijumlahkan, tetapi tidak ada median. Oleh karena itu, jika kita ingin mengetahui berapa lama waktu yang dibutuhkan untuk menyelesaikan jumlah proyek N, kita perlu melihat nilai rata-rata. Misalkan kita memiliki tiga proyek berbeda dengan σ = 1 yang sama:


Perhatikan bahwa rata-rata dijumlahkan dan 4,95 = 1,65 * 3, tetapi kolom lainnya tidak.

Sekarang mari kita tambahkan tiga proyek dengan sigma yang berbeda:


Rata-rata masih terbentuk, tetapi kenyataannya bahkan tidak dekat dengan perkiraan 3 minggu naif yang mungkin Anda harapkan. Perhatikan bahwa proyek yang sangat tidak pasti dengan σ = 2 mendominasi sisanya dalam waktu penyelesaian rata-rata. Dan untuk persentil ke-99, itu tidak hanya mendominasi, tetapi secara harfiah menyerap semua yang lain. Kami dapat memberikan contoh yang lebih besar:


Sekali lagi, satu-satunya tugas yang tidak menyenangkan terutama dominan dalam perhitungan estimasi, setidaknya untuk 99% kasus. Bahkan dalam waktu rata-rata, satu proyek gila pada akhirnya membutuhkan sekitar setengah waktu yang dihabiskan untuk semua tugas, meskipun mereka memiliki nilai yang sama dalam hal median. Untuk kesederhanaan, saya berasumsi bahwa semua tugas memiliki perkiraan waktu yang sama, tetapi ketidakpastian yang berbeda. Matematika disimpan ketika ketentuannya berubah.

Ini lucu, tetapi saya sudah lama memiliki perasaan ini. Menambahkan peringkat jarang berhasil ketika Anda memiliki banyak tugas. Sebaliknya, cari tahu tugas mana yang memiliki ketidakpastian tertinggi: tugas-tugas ini biasanya akan mendominasi waktu eksekusi rata-rata.

Diagram menunjukkan mean dan persentil ke-99 sebagai fungsi dari ketidakpastian (σ):



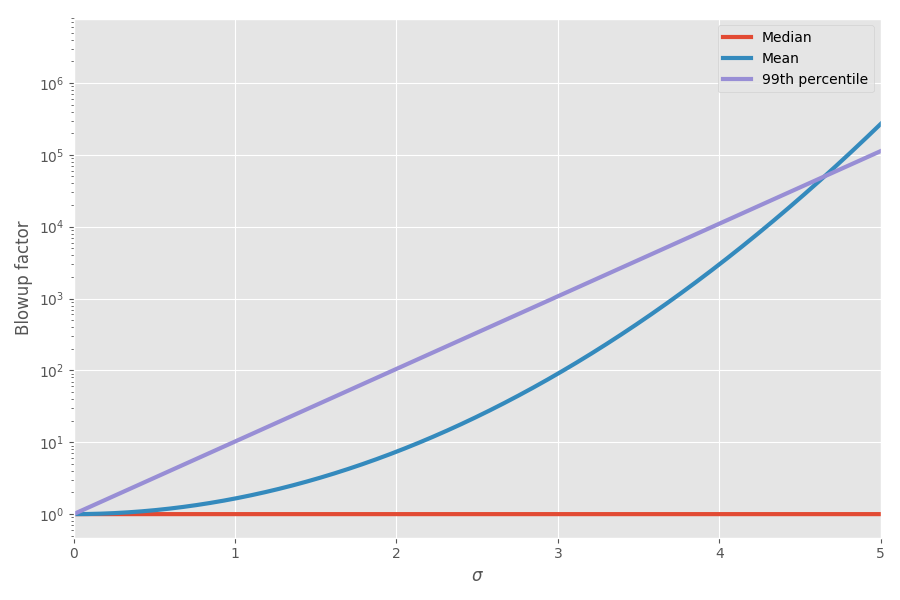
Sekarang matematika menjelaskan perasaanku! Saya mulai mempertimbangkan ini ketika merencanakan proyek. Saya benar-benar berpikir bahwa menambahkan perkiraan jadwal untuk menyelesaikan tugas-tugas sangat menyesatkan dan menciptakan gambaran yang salah tentang berapa banyak waktu seluruh proyek akan memakan waktu, karena Anda memiliki tugas miring miring yang pada akhirnya memakan waktu.

Di mana bukti empirisnya?

Untuk waktu yang lama saya menyimpannya di otak saya di bagian "model mainan penasaran", kadang-kadang berpikir bahwa ini adalah ilustrasi rapi dari fenomena dunia nyata. Tetapi suatu hari, berkeliaran di jaringan, saya menemukan set data yang menarik tentang menilai waktu proyek dan waktu aktual untuk menyelesaikannya. Fiksi!

Mari kita buat bagan sebar cepat perkiraan dan waktu aktual:



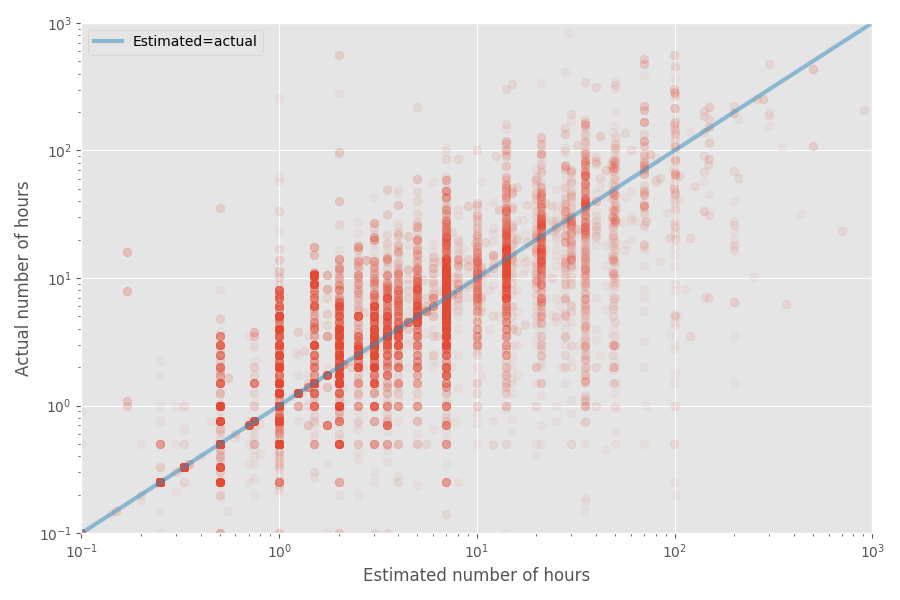
Tingkat inflasi median untuk kumpulan data ini adalah 1X, sedangkan koefisien rata-rata adalah 1,81x. Sekali lagi, ini mengkonfirmasi firasat bahwa pengembang menilai median dengan baik, tetapi rata-rata jauh lebih tinggi.

Mari kita lihat distribusi koefisien inflasi (logaritma):



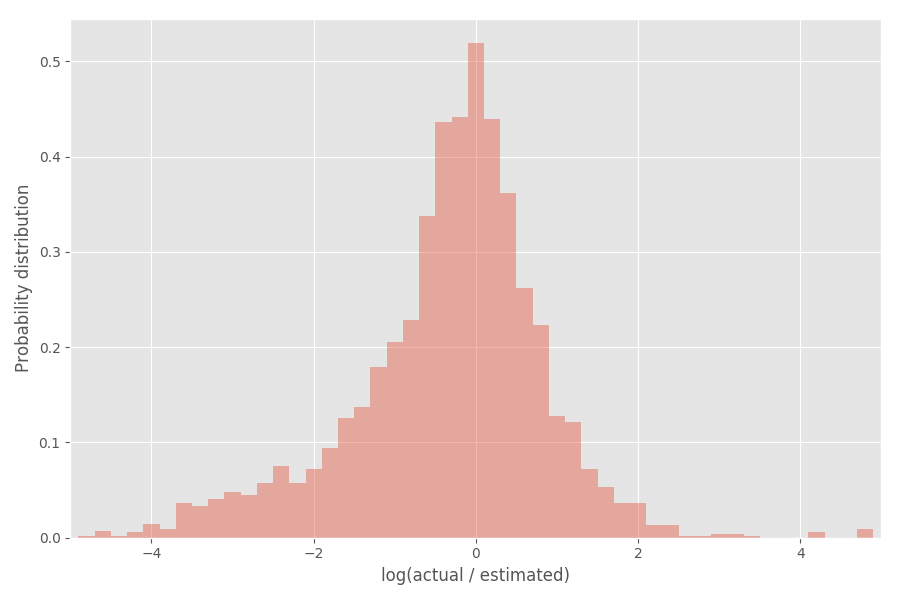
Seperti yang Anda lihat, itu cukup terpusat di sekitar 0, di mana koefisien inflasi exp (0) = 1.

Ambil alat statistik

Sekarang saya akan bermimpi sedikit dengan statistik - jangan ragu untuk melewatkan bagian ini jika tidak menarik bagi Anda. Apa yang bisa kita simpulkan dari distribusi empiris ini? Anda dapat berharap bahwa logaritma tingkat inflasi akan didistribusikan sesuai dengan distribusi normal, tetapi ini tidak sepenuhnya benar. Perhatikan bahwa σ itu sendiri acak dan bervariasi untuk setiap proyek.

Salah satu cara pemodelan yang mudah σ adalah mereka dipilih dari distribusi gamma terbalik . Jika kita mengasumsikan (seperti sebelumnya) bahwa logaritma koefisien inflasi didistribusikan sesuai dengan distribusi normal, maka distribusi "global" dari logaritma koefisien inflasi berakhir dengan distribusi Student .

Kami menerapkan distribusi siswa ke yang sebelumnya:



Konvergen, menurut pendapat saya! Parameter distribusi siswa juga menentukan distribusi gamma terbalik dari nilai σ:



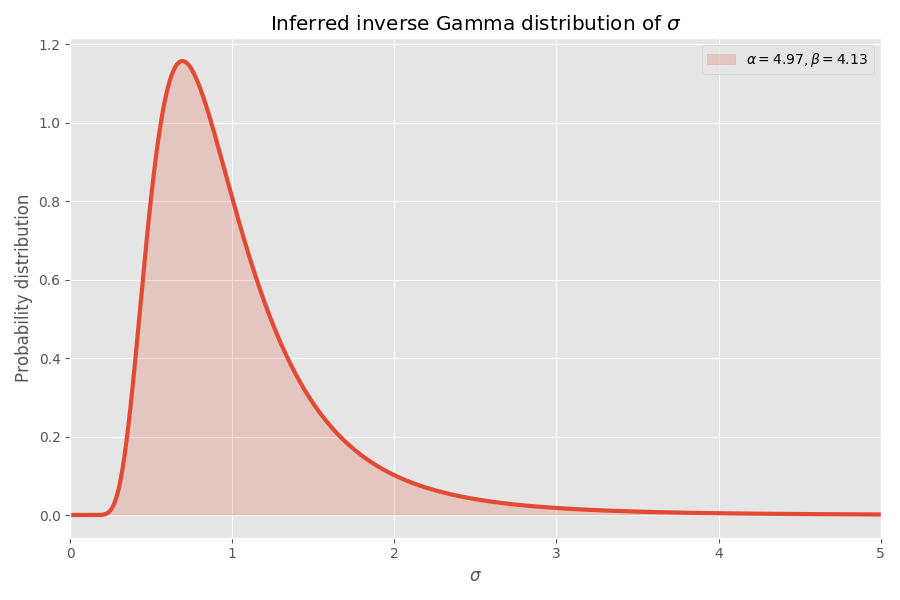
Perhatikan bahwa nilai σ> 4 sangat tidak mungkin, tetapi ketika mereka terjadi, mereka menyebabkan ledakan rata-rata beberapa ribu kali.

Mengapa tugas perangkat lunak selalu membutuhkan waktu lebih lama daripada yang Anda pikirkan

Dengan asumsi bahwa dataset ini mewakili pengembangan perangkat lunak (diragukan!), Kami dapat menarik beberapa kesimpulan lagi. Kami memiliki parameter untuk distribusi Siswa, sehingga kami dapat menghitung waktu rata-rata yang diperlukan untuk menyelesaikan tugas tanpa mengetahui σ untuk tugas ini.

Sementara tingkat inflasi median dari fit ini adalah 1x (seperti sebelumnya), tingkat inflasi 99% adalah 32x, tetapi jika Anda pergi ke persentil ke-99,99, itu adalah 55 juta kekalahan! Satu interpretasi (gratis) adalah bahwa beberapa tugas pada akhirnya tidak mungkin. Faktanya, kasus-kasus ekstrem ini memiliki dampak yang sangat besar pada rata -rata sehingga tingkat inflasi rata-rata dari setiap tugas menjadi tidak terbatas . Ini berita buruk bagi siapa pun yang mencoba memenuhi tenggat waktu!

Ringkasan

Jika model saya benar (besar jika), maka inilah yang dapat kita ketahui:

• Orang dengan baik memperkirakan waktu rata - rata untuk menyelesaikan tugas, tetapi tidak rata-rata.
  
• Waktu rata-rata jauh lebih besar daripada median karena fakta bahwa distribusinya terdistorsi (distribusi lognormal).
  
• Saat Anda menambahkan nilai untuk n tugas, segalanya menjadi lebih buruk.
  
• Tugas dengan ketidakpastian terbesar (lebih tepatnya, dari ukuran terbesar) seringkali dapat mendominasi dalam waktu rata-rata yang diperlukan untuk menyelesaikan semua tugas.
  
• Waktu eksekusi rata-rata dari tugas yang tidak kita ketahui tentang sebenarnya tak terbatas .

Catatan

• Jelas, temuan ini didasarkan hanya pada satu set data yang saya temukan di Internet. Kumpulan data lain dapat memberikan hasil yang berbeda.
  
• Model saya, tentu saja, juga sangat subyektif, seperti model statistik lainnya.
  
• Saya akan senang menerapkan model ke dataset yang jauh lebih besar untuk melihat seberapa stabil itu.
  
• Saya menyarankan agar semua tugas independen. Bahkan, mereka mungkin memiliki korelasi yang akan membuat analisis jauh lebih menyebalkan, tetapi (saya pikir) berakhir dengan kesimpulan yang sama.
  
• Jumlah nilai yang didistribusikan secara lognormal bukan nilai yang didistribusikan secara lognormal lainnya. Ini adalah kelemahan dari distribusi ini, karena Anda dapat berargumen bahwa sebagian besar tugas hanyalah jumlah dari subtugas. Alangkah baiknya jika distribusi kami berkelanjutan .
  
• Saya menghapus tugas-tugas kecil dari histogram (perkiraan waktu kurang dari atau sama dengan 7 jam), karena mereka mendistorsi analisis dan ada gelombang aneh tepat 7.
  
• Kode ada di Github , seperti biasa.