Selamat siang, pembaca yang budiman! Ini adalah artikel yang diterjemahkan kedua dalam serangkaian artikel tentang menciptakan mesin fisika oleh Chris Hecker. Jika Anda belum membiasakan diri dengan yang pertama , maka saya sarankan melakukan ini, karena semuanya akan segera menjadi jelas. Terima kasih banyak untuk mendukung terjemahan pertama: sangat menggembirakan untuk bekerja lebih jauh dan lebih banyak lagi! Selamat membaca!

Fisika, Bagian 2, Efek Sudut

Saya hanya ingin mendukung pintu dengan sesuatu yang berat sehingga penyusup tidak akan masuk. Apakah saya banyak bertanya? Saya ingin mobilnya terguling dan meledak di tempat tertentu. Saya ingin roda gigi besar macet sebelum mereka meratakan saya. Dan aku ingin buru-buru membangun sesuatu yang terlihat seperti ayunan, untuk melontarkan hadiah bersinar lucu melalui dinding benteng kastil. Siapa yang bisa menghentikan saya menerjemahkan semua ini menjadi kenyataan? Anda berasumsi bahwa lawan saya ada di dunia game, tetapi pada kenyataannya - seorang programmer mesin fisik, karena semua hal di atas didasarkan pada efek sudut. Anda dapat mengandalkan jari game-game tersebut di mana efek sudut diterapkan, belum lagi menemukan setidaknya satu di mana ini dilakukan dengan benar.

Alasan utama mengapa efek sudut (atau rotasi) tidak diterapkan dalam permainan saat ini adalah karena programmer percaya bahwa fisika yang menggambarkan gerakan rotasi terlalu rumit untuk dipahami dan diterjemahkan menjadi kenyataan. Di kelas fisika di sekolah menengah (di mana kita semua belajar hukum kedua Newton) mereka biasanya tidak berbicara tentang efek rotasi, dan tidak sepenuhnya jelas bagaimana cara beralih dari gaya yang diterapkan ke objek ke rotasi objek ini. Tentu saja, dinamika gerak rotasi sedikit lebih sulit dipahami daripada dinamika gerak linier, tetapi lebih sederhana daripada yang terlihat. Siapa pun yang dapat membuat mesin fisik sesuai dengan materi yang disajikan dalam artikel pertama siklus juga akan berhasil memasukkan efek sudut yang dijelaskan dalam artikel ini. Diharapkan setelah publikasi artikel ini, dunia akan dipenuhi dengan game yang menggunakan semua kemungkinan dan keuntungan dari efek sudut, atau setidaknya Anda dapat membuat game di mana, ketika Anda menekuk, menembak kaki teman Anda dalam pertempuran mematikan.

Pengulangan singkat

Terlepas dari kenyataan bahwa masing-masing artikel saya tentang beberapa topik unik, saya selalu membaca kembali apa yang saya tulis sebelumnya, untuk memahami di mana saya akhirnya. Saya baru saja menonton artikel pertama saya tentang fisika, dan saya senang: kami berhasil belajar banyak, dan terlebih lagi, kami tidak pernah menulis kode program atau membaca literatur tambahan! Sebelum kita mulai, mari menyegarkan materi dari artikel terakhir.



Tabel 1 berisi kesimpulan paling penting untuk dinamika padatan. Ini mengikuti dari Persamaan 1 bahwa vektor koordinat (r), vektor kecepatan (v), dan vektor percepatan (a) terkait dengan turunan (dan oleh integral, jika kita membaca dalam urutan terbalik). Sebagai pengingat, kami menandai diferensiasi waktu dengan bilangan prima (r '). r 'sama dengan dr / dt, dan r' 'sama dengan turunan waktu kedua. Dari Persamaan 2 maka gaya diasosiasikan dengan momentum linier (produk massa dan kecepatan), massa, dan akselerasi. Definisi pusat massa dapat diperoleh dari Persamaan 3 (ini adalah titik di mana semua massa dan jarak menyeimbangkan satu sama lain). Persamaan 4 menyatakan bahwa momentum linier total dari suatu padatan adalah jumlah dari semua momentumnya, yang, untuk keberuntungan kita, sama dengan momentum dari pusat massa (CM). Persamaan 5 adalah permata nyata. Ini menggunakan Persamaan 4 untuk menunjukkan bahwa percepatan pusat massa suatu benda terkait dengan gaya total (vektor dari jumlah semua gaya yang bekerja pada objek pada waktu tertentu) melalui kuantitas skalar, massa benda.

Untuk meringkas segala sesuatu yang dijelaskan dalam artikel pertama: kami belajar bahwa gaya total yang bekerja pada pusat massa kami sama dengan jumlah semua gaya yang diterapkan pada tubuh (termasuk gaya gravitasi, kereta penjahat, ledakan di dekatnya, dorongan mesin kami, dll. .). Setelah itu, kami membagi jumlah vektor ini dengan massa tubuh untuk mendapatkan percepatan CM, dan kemudian mengintegrasikan percepatan waktu untuk mendapatkan kecepatan dan koordinat tubuh.

Persamaan 5 hanyalah sebuah mahakarya! Anda akan melihat bahwa di dalamnya tidak ada konsep titik penerapan kekuatan pada tubuh, dan ini adalah titik kunci dalam menentukan bagaimana tubuh akan berputar di bawah aksi mereka. Persamaan 5 benar. Bahkan, sangat baik untuk menemukan akselerasi linier. Kami melewatkan setengah pertempuran. Tapi hal pertama yang pertama ...

Apa sudut pandangmu?

Pada artikel pertama, rotasi diabaikan, jadi kami hanya membutuhkan vektor radius dan turunannya untuk menggambarkan konfigurasi tubuh kami dalam 2D. Sekarang mari kita tambahkan nilai kinematika lain, orientasi (dilambangkan dengan huruf kapital omega - Ω), agar dapat bekerja dengan efek sudut. Untuk mengatur Ω, kita perlu memilih sistem koordinat relatif terhadap solid dan sistem koordinat dunia game, dan nilai Ω akan sama dengan perbedaan sudut di antara mereka dalam radian, seperti yang ditunjukkan pada Gambar 1.



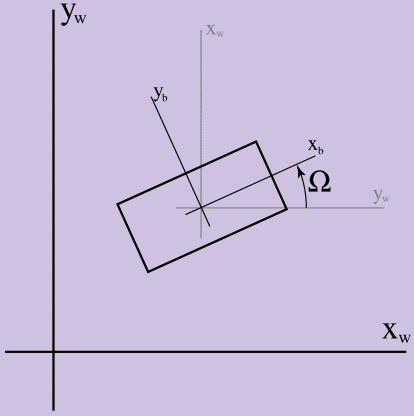Gambar 1. Definisi Ω

Dalam gambar, sumbu xw, yw adalah sumbu koordinat dunia game, dan xb, yb adalah sumbu koordinat solid. Ω lebih besar dari 0 jika dihitung berlawanan arah jarum jam. Penting di sini untuk menjelaskan mengapa kita mempelajari dinamika dunia dua dimensi sebelum pindah ke tiga dimensi: orientasi dalam 2D ​​adalah kuantitas skalar (sudut antara sistem koordinat dalam radian), sementara menentukan orientasi di dunia tiga dimensi jauh lebih sulit.

Saat tubuh berputar, nilai Ω berubah. Perubahan ini membawa kita ke kinematika lain - kecepatan sudut (dilambangkan dengan huruf kecil omega - ω). Berbeda dengan koordinat dan kecepatan linear tubuh, kami tidak menyatakan kecepatan sudut sebagai berikut - Ω '. Namun, kadang-kadang kita menunjukkan turunan kecepatan sehubungan dengan waktu, atau percepatan sudut, sebagai ω '(ini adalah nilai kinematik lain) atau sebagai α (huruf kecil alpha). Jangan salahkan saya: Saya tidak menemukan semua sebutan ini; dan di setiap buku yang saya baca ada sedikit perbedaan. Mitra sudut kami untuk Persamaan 1 adalah:

$$$$ menampilkan $$ {d ^ 2 Ω \ over {dt ^ 2}} = {dω \ over {dt}} = ω '= α $$ display $$

Persamaan 6

Seperti dalam Persamaan 1, kami membedakan ω pada waktunya untuk mendapatkan α; dan jika kita mengintegrasikan α dari waktu ke waktu, kita memperoleh ω, dll. Semua dengan analogi dengan artikel sebelumnya: mengetahui percepatan sudut α, kita dapat mengintegrasikannya dua kali untuk mendapatkan orientasi baru. Tetapi poin kuncinya di sini adalah untuk mengetahui nilai α.

Seperti yang dapat Anda bayangkan, tujuan kami untuk artikel ini adalah untuk mendapatkan analog sudut untuk masing-masing persamaan linear pada Tabel 1, dan kemudian, dengan memperhitungkan persamaan linear dan sudut dan gaya yang diterapkan pada objek, kita dapat menghitung percepatan liniernya dan percepatan sudut α. Akhirnya, kita dapat mengintegrasikan percepatan ini secara numerik untuk menemukan posisi dan orientasi baru dari tubuh kita.

Untuk mulai dengan, kita akan menghubungkan jumlah linier dan sudut bersama. Dan ini adalah trik yang agak tidak jelas di mana kecepatan sudut digunakan. Saat menghitung dalam dinamika, kita sering perlu menemukan kecepatan titik sembarang pada suatu objek. Sebagai contoh, ketika kita menghitung tumbukan benda padat, kita perlu mengetahui kecepatan titik tumbukan untuk memahami seberapa banyak tumbukan satu sama lain. Jika tubuh kita tidak berputar, kecepatan setiap titik tubuh adalah sama. Kita cukup memonitor kecepatan pusat massa tubuh, dan itu sudah cukup. Sedangkan jika tubuh kita berputar, setiap titik tubuh ini dapat memiliki kecepatan yang berbeda. Jelas, kita tidak dapat menghitung kecepatan titik tak terbatas dari tubuh kaku kita, oleh karena itu kita membutuhkan solusi yang berbeda dan lebih baik.

Salah satu metode sederhana yang digunakan untuk menemukan kecepatan linier dari setiap titik di dalam suatu objek menggunakan kecepatan sudut objek. Pertimbangkan kasus ketika tubuh hanya berputar di sekitar satu titik tetap O, tanpa mengubah koordinat tubuh. Artinya, tubuh berputar, tetapi tidak bergerak. Dari Persamaan 7 berikut cara menghitung kecepatan titik B dari benda yang berputar:

$$$$ menampilkan $$ v ^ B = ωr ^ {OB} _⟂ $$ menampilkan $$

Persamaan 7

Kita perlu mengklarifikasi beberapa poin dalam Persamaan 7, mari kita luangkan waktu untuk ini. Pertama, saya menggunakan pengindeksan atas untuk menunjukkan parameter mana yang dimiliki oleh titik-titik ini, jadi v ^ B adalah vektor kecepatan titik B dari tubuh kita. Demikian pula, r ^ OB menunjukkan vektor yang ditarik dari pusat rotasi tubuh kita O ke titik B. Huruf terbalik lucu T adalah "operator tegak lurus" yang bekerja pada vektor (seperti vektor r dalam Persamaan 7) dan memutarnya 90 derajat berlawanan arah jarum jam panah. Dengan kata lain, vektor baru dibangun yang tegak lurus dengan yang lama. Dalam dunia dua dimensi, vektor tegak lurus terhadap (x, y) adalah adil (-y, x). Anda dapat dengan mudah memeriksa kata-kata saya pada selembar kertas grafik. Mari kita bicara lebih banyak tentang ini. Besarnya vektor tegak lurus ditentukan oleh kecepatan sudut ω dan mengatur kecepatan linier v ^ B. Dalam bahasa Rusia, Persamaan 7 menunjukkan bahwa kecepatan suatu titik dari benda yang berputar dihitung dengan mengalikan vektor tegak lurus yang ditarik dari pusat rotasi dengan kecepatan sudut. Bagaimana saya mengerti itu? Baiklah, saya membacanya di buku, tetapi jelas bahwa penjelasan seperti itu tidak cukup, jadi kami membuktikan bahwa ini benar.

Mari kita buktikan kebenaran kesimpulan Persamaan 7 dalam dua tahap. Pertama, kami membuktikan bahwa nilai vektor kecepatan yang dihasilkan benar; lalu - bahwa arahnya benar. Untuk bagian pertama dari buktinya, pertimbangkan Gambar 2.



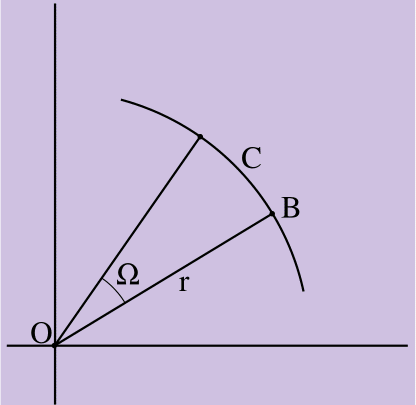Gambar 2. C = Ωr

Gambar 2 menunjukkan rotasi titik B dengan sudut yang sama dengan Ω radian dalam arah rotasi benda tegar dengan vektor jari-jari panjang r yang diarahkan dari pusat rotasi benda O ke titik B. B melewati panjang busur C, di mana C = fromr dari definisi radian. (Ukuran radian dari sudut adalah ukuran busur yang dibatasi oleh jari-jari lingkaran. Lingkaran lingkaran adalah C = 2r karena ukuran radian dari busur lingkaran adalah 2π [atau 360 derajat]).

Kecepatan suatu titik adalah perubahan koordinatnya dalam waktu. Oleh karena itu, kita dapat menemukan kecepatan titik B - dengan kata lain, besarnya vektor kecepatan - dengan membedakan persamaan gerak sehubungan dengan waktu. C = Ωr adalah persamaan gerak.

$$

$${d (Ωr) \ over {dt}} = {dΩ \ over {dt}} r = $r$$

Jari-jari diambil dari tanda diferensiasi, karena itu adalah konstanta (Titik B hanya berputar, tanpa perpindahan linier), dan turunan waktu Ω adalah ω dari Persamaan 6. Oleh karena itu, besarnya vektor B adalah vektor kecepatan ωr.

Dengan mempertimbangkan Persamaan 7, kita perhatikan bahwa besarnya vektor kecepatan sudah benar, karena tegak lurusnya tidak memengaruhi panjang vektor dan r ^ OB adalah vektor radius yang diarahkan dari O ke B. Fuh, kita setengah.

Untuk memverifikasi bahwa arah vektor kecepatan dalam Persamaan 7 benar, mari kita mulai dengan memastikan bahwa vektor kecepatan harus tegak lurus terhadap vektor radius. Asumsi ini dapat dimengerti secara intuitif, karena titik yang berputar di sekitar titik tertentu lainnya hanya dapat bergerak tegak lurus ke vektor di antara titik-titik ini. Ia tidak dapat mendekati pusat rotasi atau menjauh darinya, atau gerakan ini akan berhenti menjadi rotasi. Kami dapat mendukung asumsi kami dengan perhitungan untuk vektor, tetapi saya dijepit dalam kerangka kerja tertentu untuk volume artikel, jadi kami akan menganggap bahwa asumsi kami benar. (Jika Anda ingin membuktikannya sendiri, bedakan produk skalar dari vektor dengan panjang tetap itu sendiri.)

Akhirnya, kita harus memastikan bahwa vektor ditandai dengan benar, karena gambar tersebut menunjukkan dua vektor dengan panjang yang sama tegak lurus dengan jari-jari: v dan -v. Karena nilai Ω diukur berlawanan arah jarum jam, ω> 0 saat titik berputar searah jarum jam. Titik tegak lurus searah jarum jam, seperti halnya vektor radius. Gambar 3 menunjukkan kesimpulan dari Persamaan 7:



Gambar 3. Hubungan antara kecepatan linier dan sudut

Suplemen Persamaan 7 untuk menggambarkan rotasi benda yang bergerak. Kami menganggap gerakan benda padat sebagai gerakan sederhana pusat rotasi tubuh dan rotasi sederhana bagian tubuh di sekitar titik ini. Bagi mereka yang tertarik, ini adalah teorema Schal tentang klasifikasi gerakan.

Teorema Chall membagi gerakan kita menjadi dua komponen - linear dan angular. Biarkan pusat rotasi tubuh O menjadi satu-satunya titik bergerak, maka kita menggunakan ω untuk menghitung rotasi di sekitar titik O, dan ini memberi kita bentuk umum dari Persamaan 7:

$$$$ menampilkan $$ v ^ B = v ^ O + ^r ^ {OB} _⟂ $$ menampilkan $$

Persamaan 9

Persamaan 9 mengatakan bahwa kita dapat menghitung kecepatan titik mana pun dari benda yang bergerak menggunakan kecepatan linier pusat rotasi benda dan, di samping itu, kecepatan yang diperoleh selama rotasi benda.

Alasan untuk dorongan hati kita

Sekarang kita dapat menulis analog sudut Persamaan 2, persamaan gaya. Kita mulai dengan menentukan momentum sudut, L ^ AB dari titik B, di sekitar titik A lainnya:

$$

$${L} ^ {AB} = {\ vec r} ^ {AB} \ kali {\ vec p} ^ B$$

Persamaan 10

Momen momentum suatu titik berbeda dari momentum linier suatu titik di mana versi sudut persamaan memperhitungkan posisi benda dalam ruang. Dari sini dapat disimpulkan bahwa momentum sudut suatu titik harus diukur untuk tempat lain di dunia permainan, berbeda dengan dorongan linear yang ditentukan untuk suatu titik tertentu (produk dari massa dan kecepatannya). Ini ditunjukkan melalui indeksasi atas dalam Persamaan 10. Notasi L ^ AB mengatakan bahwa momentum sudut diukur untuk titik B dari titik A (pusat rotasi tubuh). Bayangkan panah yang menunjuk dari titik A ke titik B. Panah ini adalah vektor radius antara dua titik, artinya r ^ AB. Jadi, momentum sudut suatu titik adalah produk skalar dari vektor momentum linier dan vektor radius tegak lurus terhadapnya. Operasi ini disebut "produk skalar dengan tegak lurus", dan merupakan analog 2D untuk produk vektor 3D, tetapi kami akan membahasnya lain kali.

Jika Anda menggambarkan secara grafis apa yang mengikuti dari persamaan 10, di atas kertas - seperti yang saya lakukan pada Gambar 4 - Anda akan melihat bahwa itu menentukan ukuran bagaimana momen linier titik B "berputar". A.



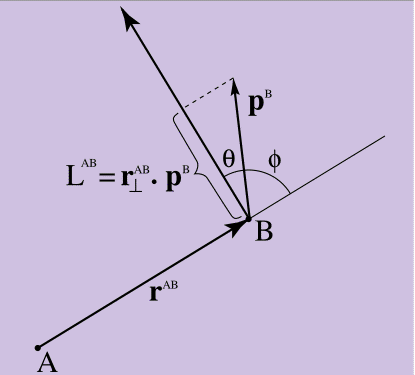Gambar 4. Momen impuls

Semuanya benar jika momentum titik B menunjuk langsung ke titik A, Persamaan 10 = 0 (karena tegak lurus dengan r membentuk sudut kanan dengan p, dan produk skalar akan menjadi 0). Semakin besar momentum B yang diarahkan tegak lurus ke A, semakin besar pula momentumnya. Seperti yang dapat dilihat pada Gambar 4, produk skalar dalam Persamaan 10 memiliki parameter cosinus sudut θ yang terlampir di antara r ^ AB tegak lurus hingga p ^ B. Jika Anda melihatnya di sisi lain, besarnya produk skalar diberikan oleh sinus sudut φ antara yang asli yang tidak tegak lurus dengan r ^ AB dan p ^ B (sinus adalah kunci lain untuk mengurai koneksi antara vektor dan produk skalar). Persamaan 10 memberikan ukuran seberapa besar momentum titik B "terlihat" dalam "arah rotasi" relatif terhadap titik A.

Juga, ketika kita menggunakan turunan dari momentum linier untuk menentukan gaya, kita akan menggunakan turunan dari momentum sudut untuk menentukan kembar sudut dari gaya - momen gaya (ditunjukkan oleh huruf kecil tau - τ).

$$

$$τ ^ {AB} = {dL ^ {AB} \ over dt} = {d ({\ vec r} ^ {AB} \ kali {\ vec p} ^ B) \ over dt} = \ vec r ^ { AB} \ kali ma ^ B = \ vec r ^ {AB} \ kali F ^ B$$

Persamaan 11

Untuk menghemat ruang, saya sedikit curang dalam Persamaan 11, melompati beberapa langkah sulit yang melibatkan menemukan turunan. Dari uraian di atas, dapat disimpulkan bahwa momen gaya berhubungan dengan gaya pada titik tertentu melalui produk skalar.

Akhirnya, kami mendapatkan persamaan dinamis yang menggunakan titik penerapan gaya, yang sebelumnya diabaikan dalam persamaan momentum linier. Persamaan 11 menggunakan produk skalar dengan tegak lurus sebagai ukuran seberapa besar gaya yang diterapkan pada titik B berputar di sekitar titik A; "kekuatan rotasi" ini disebut momen kekuatan. Persamaan 11 memungkinkan Anda untuk menemukan nilai numerik dari momen gaya - dan karenanya momentum sudut, jika kita mengintegrasikan momen gaya, mengetahui gaya yang diterapkan dan titik penerapan.

Namun, kami masih belum menerima persamaan hubungan antara momen gaya dan besaran sudut kinematika yang kita perlukan untuk memutar objek di sekitar porosnya - seperti percepatan sudut, kecepatan sudut atau orientasi sudut. Karena itu, kita tidak dapat bergerak maju sebelum menurunkan beberapa persamaan lagi.

Saat kita semua sudah menunggu

Sebelum kita membuat hubungan antara dinamika dan kinematika, kita perlu menentukan momentum sudut total, dengan analogi dengan bagaimana kita menentukan momentum linear total dalam Persamaan 4. Saya belum lupa tentang persamaan sudut untuk pusat massa dalam Persamaan 3; kita akan melihatnya dalam persamaan momentum sudut total.

Momentum sudut total dekat titik A dilambangkan dengan L ^ AT dan ditentukan oleh Persamaan 12:

$$

$$L ^ {AT} = {\ sum _ {i} {} {\ vec r ^ {Ai} \ kali p ^ i}} = {\ sum _ {i} {\ vec r ^ {Ai} \ kali m ^ iv ^ i}}$$

Persamaan 12

Persamaan 12 adalah jumlah semua momen sudut dari semua titik tubuh, diukur relatif terhadap titik A. Di sisi kanan, saya menggunakan definisi momentum linier untuk mewakili p ^ i sebagai produk dari massa dan kecepatan (mv). Ini akan berguna bagi saya di masa depan untuk membuat sesuatu dari Persamaan 12 sesuatu dengan karakter terapan yang lebih jelas. Persamaan mengatakan bahwa untuk menemukan momentum sudut total untuk objek kita, perlu untuk menjumlahkan momentum sudut semua titiknya. Untuk benda padat yang terdiri dari wajah (dan bukan dari titik terpisah), perlu untuk menghitung integral, untuk jumlah non-diskrit.

Untungnya, kita dapat menyederhanakan perhitungan kita dengan memperkenalkan kuantitas baru yang disebut "momen inersia", mirip dengan bagaimana kita memperkenalkan pusat massa untuk menyederhanakan persamaan momentum total. Ingatlah bahwa, berkat Persamaan 7, kita dapat menemukan kecepatan suatu titik melalui kecepatan sudut. Misalkan titik A dalam Persamaan 12 menjadi pusat rotasi dari Persamaan 7, dan indeks penjumlahan i dalam Persamaan 12 menjadi titik B dari Persamaan 7, maka dimungkinkan untuk mengubah Persamaan 7 ke Persamaan 12. Kita mendapatkan:

$$

$$L^{AT} = \sum _{ i} {\vec r ^{Ai} \times m^i ω \vec r^{Ai}} = ω {\sum _{ i} {m^i \vec r^{Ai} \times \vec r ^{Ai}}} = ω \sum_{ i} {m^i (\vec r ^{Ai})^2} = ωI^A$$

Persamaan 13 Saya akan

menuliskan Persamaan 13 secara lebih rinci, langkah demi langkah. Pertama, kita mengganti Persamaan 7 dengan 12 untuk mendapatkan jumlah dalam Persamaan 13. Penggantian ini memungkinkan kita untuk menggambarkan momentum sudut menggunakan kecepatan sudut. Selanjutnya, kita mengambil ω untuk penjumlahan, karena itu sama untuk semua titik padatan (kecepatan sudut ditentukan untuk seluruh tubuh, dan bukan untuk setiap titik secara terpisah), dan kami menulis massa dengan indeks i di sebelah kiri, agar lebih jelas melihat radius produk skalar -Vektor untuk diri mereka sendiri. Produk skalar ini sama dengan kuadrat dari panjang jari-jari vektor (produk skalar dari vektor apa pun dengan sendirinya = kuadrat dari panjangnya. Ingatlah bahwa operator tegak lurus tidak mengubah panjang vektor.). Akhirnya, kita menulis I ^ A untuk menunjukkan momen inersia di sekitar titik A.

Momen inersia untuk benda padat dua dimensi adalah angka yang sangat baik, karena titik-titik yang membentuk tubuh tidak dapat mengubah massa mereka atau menjauh dari pusat rotasi. Sebagai konsekuensi dari dua properti ini, jumlah dalam Persamaan 13 adalah konstan untuk setiap tubuh, sehingga kita dapat menghitungnya. Berbicara dalam bahasa Rusia, I ^ A adalah jumlah jarak yang dikuadratkan dari titik A ke semua titik tubuh lainnya, dan setiap jarak tersebut diskalakan sesuai dengan massa setiap titik. Sama seperti untuk pusat massa - jika tubuh lebih padat daripada terdiri dari titik-titik diskrit, maka jumlah akan berubah menjadi integral. Dan momen inersia akan tetap sama besarnya dan akan memiliki makna fisik yang sama.

Menentukan momen inersia dekat suatu titik adalah bertele-tele, tetapi anggaplah I ^ A sebagai ukuran seberapa sulit untuk membalikkan tubuh di sekitar titik A. Misalnya, bayangkan sebuah pensil (pensil datar). Jika kita mengukur momen inersia di dekat pusat pensil, kita mendapatkan nilai tertentu yang sama dengan jumlah kuadrat dari jarak yang diukur sesuai dengan massa setiap titik. Sedangkan jika kita mengukur kelembaman di ujung pensil yang sama, kita mendapatkan nilai yang lebih besar, karena semakin jauh titik-titik dengan massa dihilangkan, semakin besar nilai kuadrat jarak mereka. Di sini kita akan merumuskan secara matematis apa yang intuitif bagi kita: memutar pensil di tengahnya jauh lebih mudah (membacanya membutuhkan lebih sedikit usaha) daripada memutarnya di salah satu ujungnya.

Akhirnya, kami siap untuk menggambar hubungan antara persamaan sudut dinamika dan persamaan sudut kinematika. Jika kita membedakan Persamaan 13, kita mendapatkan momen total kekuatan di sebelah kiri, dan produk dari momen inersia dan percepatan sudut di sebelah kanan (I ^ A adalah konstanta, kita meletakkannya di luar tanda diferensiasi):

$$

$$τ^{AT} = {dL^{AT} \over dt} = {d( I^A ω) \over dt} = I^A ω = I^A α$$

Persamaan 14 Persamaan

ini adalah persamaan sudut dari Persamaan 5; sebenarnya, itu adalah F = ma untuk dinamika sudut. Ini adalah persamaan dari hubungan momen total kekuatan dan percepatan sudut tubuh melalui momen skalar inersia. Jika kita mengetahui momen gaya yang diberikan pada tubuh kita, kita dapat menemukan percepatan sudutnya, dan kemudian kecepatan sudut dan orientasi dalam ruang melalui integrasi - membagi momen gaya dengan momen inersia.

Algoritma dinamika

Dia hampir tidak melihat kita melalui pusaran persamaan ini, tetapi semuanya adalah bagian integralnya. Kami telah memperoleh cukup persamaan untuk mendapatkan dinamika luar biasa dari dunia dua dimensi dengan kekuatan dan momen kekuatan yang diberikan secara sewenang-wenang menggerakkan dan memutar objek-objek kita. Bagaimana cara menggunakan persamaan ini? Di bawah ini adalah algoritma dasar:

1. Temukan nilai pusat massa dan momen inersia di pusat massa.
2. Atur koordinat awal tubuh, orientasinya dalam ruang, kecepatan linier dan sudutnya.
3. Memperhatikan semua kekuatan yang bekerja pada tubuh dan titik-titik aplikasi mereka.
4. Temukan resultan dari semua gaya dan membaginya dengan massa tubuh untuk menemukan percepatan linear dari pusat massa (Persamaan 5).
5. , , , ( 11).
6. ( 14).
7. , , ( ).
8. , 3.

Dalam algoritma di atas, hanya ada dua langkah yang belum saya jelaskan. Pertama, bagaimana cara menghitung momen inersia pada Langkah 1 untuk objek padat? Kedua, bagaimana mengatasi masalah dengan kekuatan dari Langkah 3? Jawaban untuk pertanyaan pertama dapat ditemukan dalam contoh kode sederhana, yang akan saya tinggalkan dalam aplikasi di akhir artikel ini (Anda akan mengintegrasikan objek dengan wilayahnya). Banyak buku tentang dinamika mengandung momen inersia yang dihitung untuk bentuk objek yang sering dijumpai dalam aplikasi di bagian paling akhir, jadi Anda tidak harus menampilkannya sendiri setiap kali.

Jawaban untuk pertanyaan tentang bagaimana menghitung kekuatan dari Langkah 3 tergantung pada aplikasi, tetapi saya akan memberikan beberapa rekomendasi umum. Pertama, gaya seperti gravitasi, selalu diarahkan dalam satu arah (turun, dalam kasus gravitasi), tidak menciptakan momen kekuatan, karena mereka menarik semua titik pada saat yang sama dalam arah yang sama, meskipun kita kami menerapkan kekuatan-kekuatan ini langsung ke pusat massa. Gaya yang mirip dengan gaya elastis diterapkan pada titik tertentu dari objek, mereka akan menciptakan momen kekuatan, oleh karena itu kami mempertimbangkannya dalam kasus umum. Seperti yang kita lihat di artikel pertama, gaya gesekan adalah gaya yang sama yang diarahkan ke arah yang berlawanan dengan kecepatan tubuh.

Anda dapat membuat model fisik sederhana yang menunjukkan kekuatan gesekan, dan cukup menerapkan gaya pada pusat massa, atau Anda dapat memilih bagian mana dari objek yang akan menerapkan gaya gesekan, dan melakukan ini, yang dapat menciptakan momen kekuatan yang bekerja pada objek. Kekuatan yang dialami tubuh dalam tabrakan sedikit lebih sulit, dan kita akan mengenalnya di artikel selanjutnya. Pasukan seperti dorongan mesin roket harus dianggap sebagai kekuatan dengan titik aplikasi (dalam hal ini, jika salah satu mesin gagal, Anda akan mulai memutar porosnya sampai Anda menyesuaikan roda kemudi untuk menyeimbangkan momen kekuatan!). Jika Anda menginginkan sesuatu yang mirip dengan sinar gravitasi dari UFO, maka gaya ini harus dihitung sebagai gaya gravitasi dan tidak menciptakan momen gaya, atau harus diterapkan pada titik tertentu pada objek,dan apakah itu akan berputar di sekitar titik ini saat bangkit? Pilihan ada di tangan Anda. Poin kuncinya adalah jangan takut untuk bereksperimen dengan kekuatan yang berbeda yang dihitung dengan cara yang berbeda, karena sekarang Anda memiliki simulator nyata dari grafik dua dimensi, cobalah berbagai jenis kekuatan!

Saya meninggalkan semua kode dan tautan yang Anda butuhkan di situs web saya karena tidak ada lagi ruang yang tersisa. Dalam aplikasi sederhana saya, saya menerapkan algoritma dinamika dunia dua dimensi, dan juga menambahkan objek yang diikat oleh pegas; mereka berputar di sekitar porosnya, dan kadang-kadang bahkan bertabrakan dengan dinding, berputar. Tapi saya akan membicarakan ini lain kali. Ikuti tautan untuk lebih banyak literatur dan aplikasi sederhana untuk Windows 32 dan Macintosh.

Sangat jarang, Chris Hecker mengalami efek momen inersia, tetapi biasanya itu berlalu cukup cepat. Pasukan dapat diterapkan ke checker@bix.com.

Catatan penerjemah: permainan kata pun disajikan di sini, topik artikel dan isinya dimainkan.

Umpan Balik PS diterima. Komentar Anda dapat meningkatkan kualitas pekerjaan. Terima kasih

PPS Penulis terjemahan mengucapkan terima kasih khusus kepada pengguna berez dan Vasily Tereshkov karena telah mengedit terjemahan. Terima kasih