Array Antena Adaptif: Bagaimana Cara Kerjanya? (Dasar-dasar)

Hari yang baik

Beberapa tahun terakhir saya telah mencurahkan untuk penelitian dan pembuatan berbagai algoritma untuk pemrosesan spasial sinyal dalam array antena adaptif, dan saya terus melakukan ini sebagai bagian dari pekerjaan saya saat ini. Di sini saya ingin berbagi pengetahuan dan keripik yang saya temukan. Saya harap ini bermanfaat bagi orang-orang yang mulai mempelajari bidang pemrosesan sinyal ini atau hanya tertarik.

Apa itu array antena adaptif?

Array antena adalah seperangkat elemen antena, yang diatur dalam ruang dengan cara tertentu. Untuk menyederhanakan struktur susunan antena adaptif, yang akan kami pertimbangkan, dapat direpresentasikan dalam bentuk berikut:


Susunan antena adaptif sering disebut "antena pintar" (antena pintar ). Susunan antena "pintar" dibuat oleh unit pemrosesan sinyal spasial dan algoritma yang diterapkan di dalamnya. Algoritma ini menganalisis sinyal yang diterima dan membentuk satu set bobot$$ $ inline $ w_1 ... w_N $ inline $ yang menentukan amplitudo dan fase awal sinyal untuk masing-masing elemen. Distribusi fase amplitudo yang diberikan menentukan pola directivity seluruh kisi secara keseluruhan. Kemampuan untuk mensintesis pola radiasi dari bentuk yang diperlukan dan mengubahnya selama pemrosesan sinyal adalah salah satu fitur utama dari susunan antena adaptif, yang memungkinkan untuk memecahkan berbagai masalah . Tetapi hal pertama yang pertama.

Bagaimana pola radiasi terbentuk?

Pola radiasi mencirikan kekuatan sinyal yang dipancarkan ke arah tertentu. Untuk kesederhanaan, kami menempatkan elemen kisi isotropik, yaitu untuk masing-masing dari mereka, kekuatan sinyal yang dipancarkan tidak tergantung pada arah. Amplifikasi atau pelemahan daya yang dipancarkan oleh larik dalam arah tertentu diperoleh karena gangguan gelombang elektromagnetik yang dipancarkan oleh berbagai elemen larik antena. Pola interferensi yang stabil untuk EMW hanya mungkin jika mereka koheren , mis. perbedaan fase dari sinyal tidak boleh berubah dengan waktu. Dalam kasus ideal, masing-masing elemen array antena harus memancarkan sinyal harmonik pada frekuensi pembawa yang sama$$ $ inline $ f_ {0} $ inline $ . Namun, dalam praktiknya, perlu untuk bekerja dengan sinyal pita sempit yang memiliki spektrum lebar terbatas$$ $ inline $ \ Delta f << f_ {0} $ inline $ .
Biarkan semua elemen AR memancarkan sinyal yang sama dengan amplitudo kompleks$$ $ inline $ x_n (t) = u (t) $ inline $ . Kemudian, pada penerima jarak jauh , sinyal yang diterima dari elemen ke-n dapat direpresentasikan dalam bentuk analitis :

$$$$ tampilkan $$ a_n (t) = u (t- \ tau_n) e ^ {i2 \ pi f_0 (t- \ tau_n)} $$ tampilkan $$

dimana$$ $ inline $ \ tau_n $ inline $ - keterlambatan dalam propagasi sinyal dari elemen antena ke titik penerimaan.
Sinyal semacam itu adalah "kuasi-harmonik," dan untuk memenuhi kondisi koherensi, perlu bahwa keterlambatan maksimum dalam perambatan gelombang elektromagnetik antara dua elemen jauh lebih kecil dari waktu karakteristik perubahan amplop sinyal$$ $ inline $ T $ inline $ , yaitu$$ $ inline $ u (t- \ tau_n) ≈ u (t- \ tau_m) $ inline $ . Dengan demikian, kondisi untuk koherensi sinyal pita sempit dapat ditulis sebagai berikut:

$$$$ menampilkan $$ T≈ \ frac {1} {\ Delta f} >> \ frac {D_ {max}} {c} = maks (\ tau_k- \ tau_m) $$ menampilkan $$

dimana$$ $ inline $ D_ {max} $ inline $ - jarak maksimum antara elemen AR , dan$$ $ inline $ dengan $ inline $ Apakah kecepatan cahaya.

Saat menerima sinyal, penjumlahan yang koheren dilakukan secara digital di unit pemrosesan spasial. Dalam hal ini, nilai kompleks dari sinyal digital pada output dari blok ini ditentukan oleh ekspresi:

$$$$ menampilkan $$ y = \ jumlah_ {n = 1} ^ Nw_n ^ * x_n $$ menampilkan $$

Lebih mudah untuk menyajikan ekspresi terakhir dalam bentuk produk skalar vektor kompleks N-dimensi dalam bentuk matriks:

$$$$ menampilkan $$ y = (\ textbf {w}, \ textbf {x}) = \ textbf {w} ^ H \ textbf {x} $$ display $$

di mana w dan x adalah vektor kolom, dan$$ $ inline $ (.) ^ H $ inline $ - Operasi pasangan Hermitian .

Representasi vektor sinyal adalah salah satu dasar ketika bekerja dengan array antena, karena sering menghindari perhitungan matematika yang rumit. Selain itu, identifikasi sinyal yang diterima pada saat tertentu dengan vektor sering memungkinkan kita untuk abstrak dari sistem fisik nyata dan memahami apa yang sebenarnya terjadi dari sudut pandang geometri.

Untuk menghitung pola directivity array antena, perlu untuk secara mental dan konsisten "menjalankan" di atasnya satu set gelombang pesawat dari semua arah yang mungkin. Dalam hal ini, nilai-nilai elemen vektor x dapat direpresentasikan sebagai berikut:

$$$$ menampilkan $$ x_n = s_n = \ exp \ {- i (\ textbf {k} (\ phi, \ theta), \ textbf {r} _n) \} $$ menampilkan $$

di mana k adalah vektor gelombang$$ $ inline $ \ phi $ inline $ dan$$ $ inline $ \ theta $ inline $ - sudut azimut dan sudut elevasi yang mencirikan arah kedatangan gelombang bidang,$$ $ inline $ \ textbf {r} _n $ inline $ - mengoordinasikan elemen antena,$$ $ inline $ s_n $ inline $ - elemen vektor pentahapan s dari gelombang bidang dengan vektor gelombang k (dalam literatur bahasa Inggris, vektor pentahapan disebut vektor steerage). Ketergantungan kuadrat dari amplitudo y pada$$ $ inline $ \ phi $ inline $ dan$$ $ inline $ \ theta $ inline $ menentukan pola directivity array antena pada penerimaan untuk vektor koefisien bobot tertentu yang diberikan w .

Fitur array antena

Lebih mudah untuk mempelajari sifat-sifat umum dari pola radiasi susunan antena pada susunan antena yang sama linier dalam bidang horizontal (mis., Pola berkas hanya bergantung pada sudut azimut)$$ $ inline $ \ phi $ inline $ ) Nyaman dari dua sudut pandang: perhitungan analitik dan presentasi visual.

Kami menghitung DN untuk vektor satuan berat ($$ $ inline $ w_n = 1, n = 1 ... N $ inline $ ), mengikuti pendekatan yang dijelaskan di atas .


Sebagai hasilnya, kita mendapatkan:

$$$$ menampilkan $$ F (\ phi) = | y | ^ 2 = \ frac {\ sin ^ 2 (\ pi \ frac {Nd} {\ lambda} \ sin \ phi)} {\ sin ^ 2 (\ pi \ frac {d} {\ lambda} \ sin \ phi)} $$ menampilkan $$

Frekuensi pola radiasi

Pola radiasi yang dihasilkan dari susunan antena adalah fungsi periodik dari sinus sudut. Ini berarti bahwa untuk nilai-nilai tertentu dari rasio d / λ , ia memiliki difraksi (tambahan) maksimum.
Pola antena tidak normal untuk N = 5
Pola radiasi normal antena array untuk N = 5 di sistem koordinat kutub

Posisi "difraktionis" dapat dilihat langsung dari rumus untuk GNB. Namun, kami akan mencoba memahami dari mana mereka berasal secara fisik dan geometris (dalam ruang dimensi N).

Unsur-unsur vektor pentahapan adalah eksponen kompleks$$ $ inline $ e ^ {i \ Psi n} $ inline $ yang nilainya ditentukan oleh nilai sudut umum$$ $ inline $ \ Psi = 2 \ pi \ frac {d} {\ lambda} \ sin \ phi $ inline $ . Jika ada dua sudut umum yang sesuai dengan arah berbeda kedatangan gelombang pesawat, untuk itu$$ $ inline $ \ Psi_1 = \ Psi_2 + 2 \ pi m $ inline $ , maka ini berarti dua hal:

• Secara fisik: bidang gelombang depan yang berasal dari arah ini menginduksi distribusi fase amplitudo yang identik dari gelombang elektromagnetik pada elemen-elemen array antena.
• Secara geometris: vektor pentahapan untuk dua arah ini bertepatan.

Arah kedatangan gelombang yang terhubung dengan cara serupa setara dari sudut pandang array antena dan tidak dapat dibedakan satu sama lain.

Bagaimana cara menentukan wilayah sudut di mana hanya satu maksimum utama dari MD selalu terletak? Kami akan melakukan ini di sekitar nol azimuth karena alasan berikut: pergeseran fase antara dua elemen yang berdekatan harus terletak pada interval dari$$ $ inline $ - \ pi $ inline $ sebelumnya$$ $ inline $ \ pi $ inline $ .

$$$$ tampilkan $$ - \ pi <2 \ pi \ frac {d} {\ lambda} \ sin \ phi <\ pi $$ tampilkan $$

Memecahkan ketidaksetaraan ini, kami memperoleh kondisi pada wilayah keunikan di lingkungan nol:

$$$$ menampilkan $$ | \ sin \ phi | <\ frac {\ lambda} {2d} $$ menampilkan $$

Dapat dilihat bahwa ukuran wilayah keunikan dalam sudut tergantung pada rasio d / λ . Jika d = 0,5 λ , maka setiap arah kedatangan sinyal adalah "individual", dan wilayah keunikan mencakup rentang sudut penuh. Jika d = 2.0 λ , maka arah 0, ± 30, ± 90 adalah setara. Lobus difraksi muncul pada pola radiasi.

Biasanya, lobus difraksi cenderung menekan menggunakan elemen antena terarah. Dalam hal ini, pola radiasi array antena yang lengkap adalah produk dari pola satu elemen dan array elemen isotropik. Parameter DN dari satu elemen biasanya dipilih berdasarkan kondisi pada wilayah keunikan array antena.

Lebar lobus utama

Formula rekayasa untuk memperkirakan lebar lobus utama sistem antena dikenal secara luas :$$ $ inline $ \ Delta \ phi ≈ \ frac {\ lambda} {D} $ inline $ di mana D adalah ukuran karakteristik antena. Formula ini digunakan untuk berbagai jenis antena, termasuk yang SLR. Kami menunjukkan bahwa itu juga berlaku untuk array antena.

Kami menentukan lebar lobus utama dengan nol pertama MD di sekitar maksimum utama. Numerator ekspresi untuk$$ $ inline $ F (\ phi) $ inline $ lenyap pada$$ $ inline $ \ sin \ phi = m \ frac {\ lambda} {dN} $ inline $ . Nol pertama sesuai dengan m = ± 1. Dengan asumsi$$ $ inline $ \ frac {\ lambda} {dN} << 1 $ inline $ kita dapatkan$$ $ inline $ \ Delta \ phi = 2 \ frac {\ lambda} {dN} $ inline $ .

Biasanya, lebar AR directivity beam ditentukan oleh tingkat daya setengah (-3 dB). Dalam hal ini, gunakan ungkapan:

$$$$ menampilkan $$ \ Delta \ phi≈0.88 \ frac {\ lambda} {dN} $$ menampilkan $$

Lebar lobus utama dapat dikontrol dengan menetapkan nilai amplitudo yang berbeda untuk koefisien bobot array antena. Pertimbangkan tiga distribusi:

• Distribusi amplitudo seragam (bobot 1):$$ $ inline $ w_n = 1 $ inline $ .
• Nilai amplitudo jatuh ke tepi kisi (bobot 2):$$ $ inline $ w_n = 0,5 + 0,3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $
• Nilai amplitudo meningkat ke tepi kisi (bobot 3):$$ $ inline $ w_n = 0.5-0.3 \ cos (2 \ pi \ frac {n-1} {N} - \ pi \ frac {N-1} {N}) $ inline $

Gambar tersebut menunjukkan pola radiasi normal yang dihasilkan pada skala logaritmik:
Kecenderungan berikut dapat diamati dari gambar: distribusi amplitudo dari koefisien berat menurun menuju tepi kisi mengarah ke pelebaran lobus utama MD, tetapi untuk penurunan tingkat lobus samping. Amplitudo meningkat ke arah tepi susunan antena, sebaliknya, menyebabkan penyempitan lobus utama dan peningkatan tingkat sisi. Lebih mudah untuk mempertimbangkan membatasi kasus di sini:

1. Amplitudo dari koefisien bobot semua elemen kecuali yang ekstrim sama dengan nol. Bobot untuk elemen ekstrem sama dengan kesatuan. Dalam hal ini, kisi menjadi setara dengan AR dua elemen dengan periode D = (N-1) d . Tidak sulit memperkirakan berdasarkan rumus di atas, lebar kelopak utama. Dalam hal ini, lateral akan berubah menjadi maxima difraksi dan sejajar dengan maksimum utama.
2. Berat elemen pusat sama dengan satu, dan sisanya menjadi nol. Dalam hal ini, pada dasarnya kami mendapat satu antena dengan pola radiasi isotropik.

Arah maksimum utama

Jadi, kami melihat bagaimana Anda dapat menyesuaikan lebar lobus utama dari AP AR . Sekarang mari kita lihat bagaimana mengarahkan arah. Ingat ekspresi vektor untuk sinyal yang diterima. Misalkan kita ingin pola radiasi maksimum terlihat dalam arah tertentu$$ $ inline $ \ phi_0 $ inline $ . Ini berarti bahwa daya maksimum harus diambil dari arah ini. Vektor pentahapan sesuai dengan arah ini$$ $ inline $ \ textbf {s} (\ phi_0) $ inline $ dalam ruang vektor N- dimensi, dan daya yang diterima didefinisikan sebagai kuadrat dari produk skalar vektor pentahapan ini dengan vektor koefisien berat w . Produk skalar dari dua vektor adalah maksimal ketika mereka collinear , yaitu$$ $ inline $ \ textbf {w} = \ beta \ textbf {s} (\ phi_0) $ inline $ , di mana β adalah beberapa faktor normalisasi. Jadi, jika kita memilih vektor bobot yang sama dengan vektor pentahapan untuk arah yang diinginkan, maka kita akan memutar pola radiasi maksimum.

Pertimbangkan bobot berikut sebagai contoh:$$ $ inline $ \ textbf {w} = \ textbf {s} (10 °) $ inline $

$$$$ tampilkan $$ w_n = \ exp \ {i2 \ pi \ frac {d} {\ lambda} (n-1) \ sin (10 \ pi / 180) \} $$ tampilkan $$

Sebagai hasilnya, kami memperoleh pola radiasi dengan maksimum utama dalam arah 10 °.

Sekarang kami menerapkan bobot yang sama, tetapi tidak untuk penerimaan sinyal, tetapi untuk transmisi. Di sini perlu dipertimbangkan bahwa ketika mentransmisikan sinyal, arah vektor gelombang dibalik. Ini berarti bahwa elemen-elemen dari vektor pentahapan untuk penerimaan dan pengiriman berbeda dalam tanda dalam eksponen, yaitu saling berhubungan oleh konjugasi kompleks. Akibatnya, kita mendapatkan maksimum pola radiasi ke arah -10 °, yang tidak sesuai dengan maksimum sinyal terima pada koefisien bobot yang sama. Untuk memperbaiki situasi, perlu untuk menerapkan konjugasi kompleks juga ke koefisien berat.

Fitur yang dijelaskan dari pembentukan balok untuk penerimaan dan transmisi harus selalu diingat ketika bekerja dengan susunan antena.

Mari kita bermain dengan pola radiasi

Sedikit yang tertinggi

Kami mengajukan masalah untuk membentuk dua maksimum utama dari pola radiasi dalam arah: -5 ° dan 10 °. Untuk melakukan ini, kami memilih jumlah tertimbang vektor pentahapan untuk arah yang sesuai sebagai vektor bobot.

$$$$ menampilkan $$ \ textbf {w} = \ beta \ textbf {s} (10 °) + (1- \ beta) \ textbf {s} (- 5 °) $$ menampilkan $$

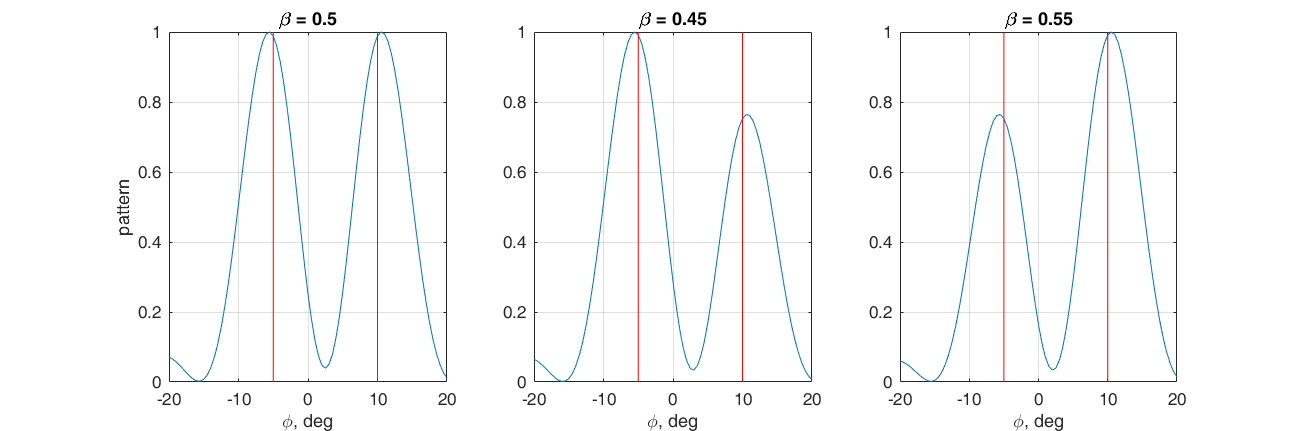
Dengan menyesuaikan koefisien β , rasio antara lobus utama dapat disesuaikan. Di sini lagi, lebih mudah untuk melihat apa yang terjadi di ruang vektor. Jika β lebih besar dari 0,5, maka vektor bobot terletak lebih dekat ke s (10 °), sebaliknya ke s (-5 °). Semakin dekat vektor bobot ke salah satu fasor, semakin besar produk skalar yang sesuai, dan karenanya besarnya maksimum ND yang sesuai .

Namun, perlu dipertimbangkan bahwa kedua kelopak utama memiliki lebar yang terbatas, dan jika kita ingin menyelaraskan dalam dua arah yang dekat, maka kelopak ini akan bergabung menjadi satu, berorientasi ke beberapa arah tengah.

Satu maksimum dan nol

Sekarang mari kita coba menyesuaikan pola radiasi maksimum ke arah$$ $ inline $ \ phi_1 = 10 ° $ inline $ dan secara bersamaan menekan sinyal yang datang dari arah$$ $ inline $ \ phi_2 = -5 ° $ inline $ . Untuk ini, perlu mengatur nol untuk sudut yang sesuai. Anda dapat melakukan ini sebagai berikut:

$$$$ menampilkan $$ \ textbf {w} = \ textbf {s} _1- \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {N} \ textbf {s} _2 $$ display $$ $$

dimana$$ $ inline $ \ textbf {s} _1 = \ textbf {s} (10 °) $ inline $ , dan$$ $ inline $ \ textbf {s} _2 = \ textbf {s} (- 5 °) $ inline $ .

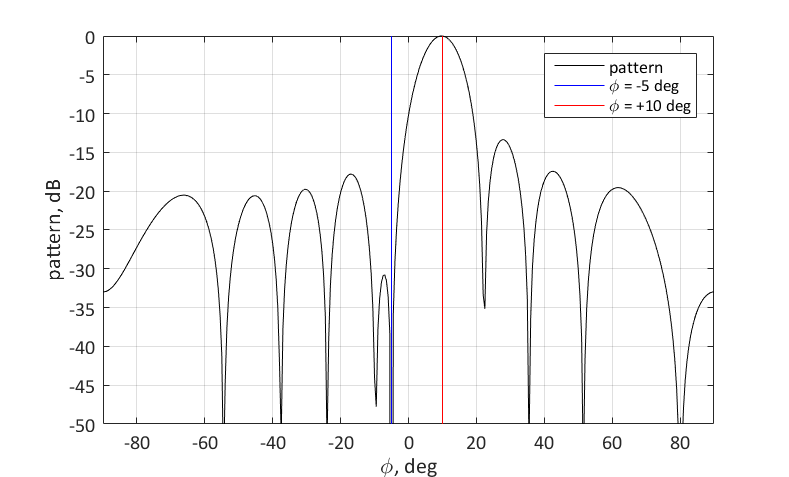
Arti geometris dari pemilihan vektor berat adalah sebagai berikut. Kami ingin vektor ini w memiliki proyeksi maksimum$$ $ inline $ \ textbf {s} _1 $ inline $ dan ortogonal ke vektor$$ $ inline $ \ textbf {s} _2 $ inline $ . Vektor$$ $ inline $ \ textbf {s} _1 $ inline $ dapat direpresentasikan sebagai dua istilah: vektor collinear$$ $ inline $ \ textbf {s} _2 $ inline $ dan vektor ortogonal$$ $ inline $ \ textbf {s} _2 $ inline $ . Untuk memenuhi pernyataan masalah, perlu untuk memilih komponen kedua sebagai vektor koefisien berat w . Komponen collinear dapat dihitung dengan mendesain vektor$$ $ inline $ \ textbf {s} _1 $ inline $ untuk menormalkan vektor$$ $ inline $ \ frac {\ textbf {s} _2} {\ sqrt {N}} $ inline $ menggunakan produk skalar.

$$$$ menampilkan $$ \ textbf {s} _ {1 ||} = \ frac {\ textbf {s} _2} {\ sqrt {N}} \ frac {\ textbf {s} _2 ^ H \ textbf {s} _1} {\ sqrt {N}} $$ menampilkan $$

Dengan demikian, kurangi dari vektor pentahapan awal$$ $ inline $ \ textbf {s} _1 $ inline $ komponen collinear-nya, kita memperoleh vektor bobot yang diinginkan.

Beberapa catatan tambahan

1. Di mana-mana di atas, saya menghilangkan pertanyaan untuk menormalkan vektor bobot, mis. panjangnya. Jadi, normalisasi vektor bobot tidak mempengaruhi karakteristik pola radiasi susunan antena: arah pepatah utama, lebar lobus utama, dll. Dapat juga ditunjukkan bahwa normalisasi ini tidak mempengaruhi SNR pada output blok pemrosesan spasial. Dalam hal ini, ketika mempertimbangkan algoritma pemrosesan sinyal spasial, saya biasanya menerima normalisasi satuan dari vektor bobot, mis.$$ $ inline $ \ textbf {w} ^ H \ textbf {w} = 1 $ inline $
2. Kemungkinan untuk pembentukan dasar antena ditentukan oleh jumlah elemen N. Semakin banyak elemen, semakin luas kemungkinan. Semakin banyak derajat kebebasan dalam penerapan pemrosesan berat spasial, semakin banyak pilihan untuk bagaimana "memutar" vektor bobot dalam ruang dimensi-N.
3. Saat menerima pola pancaran antena , susunan antena tidak ada secara fisik, dan semua ini hanya ada dalam "imajinasi" unit komputasi yang memproses sinyal. Ini berarti bahwa pada saat yang sama, dimungkinkan untuk mensintesis beberapa MDs dan secara mandiri memproses sinyal yang datang dari arah yang berbeda. Dalam hal transmisi, semuanya agak lebih rumit, tetapi juga memungkinkan untuk mensintesis beberapa MDs untuk mentransmisikan berbagai aliran data. Teknologi dalam sistem komunikasi ini disebut MIMO .
4. Dengan menggunakan kode matlab yang disediakan, Anda dapat bermain sendiri dengan NAM
   
   Kode

   % antenna array settings N = 10; % number of elements d = 0.5; % period of antenna array wLength = 1; % wavelength mode = 'receiver'; % receiver or transmitter % weights of antenna array w = ones(N,1); % w = 0.5 + 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = 0.5 - 0.3*cos(2*pi*((0:N-1)-0.5*(N-1))/N).'; % w = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+10/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % b = 0.5; w = b*exp(2i*pi*d/wLength*sin(+3/180*pi)*(0:N-1)).' + (1-b)*exp(2i*pi*d/wLength*sin(-3/180*pi)*(0:N-1)).'; % s1 = exp(2i*pi*d/wLength*sin(10/180*pi)*(0:N-1)).'; % s2 = exp(2i*pi*d/wLength*sin(-5/180*pi)*(0:N-1)).'; % w = s1 - (1/N)*s2*s2'*s1; % w = s1; % normalize weights w = w./sqrt(sum(abs(w).^2)); % set of angle values to calculate pattern angGrid_deg = (-90:0.5:90); % convert degree to radian angGrid = angGrid_deg * pi / 180; % calculate set of steerage vectors for angle grid switch (mode) case 'receiver' s = exp(2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); case 'transmitter' s = exp(-2i*pi*d/wLength*bsxfun(@times,(0:N-1)',sin(angGrid))); end % calculate pattern y = (abs(w'*s)).^2; %linear scale plot(angGrid_deg,y/max(y)); grid on; xlim([-90 90]); % log scale % plot(angGrid_deg,10*log10(y/max(y))); % grid on; % xlim([-90 90]); 

   
   

Tugas apa yang dapat diselesaikan dengan bantuan array antena adaptif?

Terima kasih atas perhatian anda