Ini adalah terjemahan dari artikel oleh Eliezer Yudkovsky dari siklus sains populer yang ditujukan untuk interpretasi multivariat mekanika kuantum. Awal siklus diterjemahkan ke dalam hub , tetapi kemudian penerjemah tampaknya lelah. Dapat dipahami - materinya sangat banyak. Yudkovsky suka menyebarkan pemikiran di atas pohon. Di sisi lain, materinya sangat kompleks, dan pengulangan hal yang sama dengan kata-kata yang berbeda memungkinkan gambar di kepala pembaca yang tidak siap untuk setidaknya tetap disimpan. Saya tidak akan melakukan untuk melanjutkan terjemahan dari seluruh siklus, tetapi saya akan mencoba menerjemahkan beberapa artikel yang paling penting.

Saya akan melewatkan artikel dalam seri tentang ruang keadaan ( klasik dan kuantum ) - konsepnya banyak digunakan di mana, dan harus akrab bagi pembaca yang terlatih secara teknis. Dan juga melewatkan integral jalur Feynman - mereka dapat ditemukan di sumber sains populer yang sangat baik.

Tetapi posting selanjutnya menjawab pertanyaan penting. Jika dunia "nyata" pada tingkat fundamental adalah kuantum, di mana semuanya membingungkan dan semuanya saling mempengaruhi, dari mana sistem klasik berasal? Mengapa kita melihat fenomena kuantum "alami" begitu jarang dalam kehidupan sehari-hari? Inilah yang penulis sebut "halusinasi klasik." Misalnya, mengapa pencipta komputer kuantum perlu melakukan upaya luar biasa untuk menjaga sistem dalam keadaan terjerat "alami"?

Penafian: Saya bukan fisikawan profesional atau penerjemah profesional (serta penulis asli).

Decoherence

Untuk memahami proses kuantum yang disebut dekoherensi, pertama-tama Anda perlu memahami bagaimana keadaan khusus kebebasan kuantum dihancurkan - yaitu, bagaimana tepatnya sistem kuantum beralih dari keadaan kemerdekaan ke keadaan keterikatan.

Kemandirian kuantum, seperti yang kita ingat , adalah suatu keadaan khusus, "persegi panjang" dari distribusi amplitudo yang difaktorkan dengan baik. Artinya, ini dapat direpresentasikan sebagai produk dari distribusi bagian-bagian penyusun sistem, yang bagi kita terlihat seperti "partikel terpisah".

Turis pemalu yang mengunjungi dunia kuantum kita kadang-kadang mengambil ketiadaan distribusi "persegi panjang" sedemikian rupa untuk suatu hubungan misterius khusus antar partikel. Oleh karena itu istilah yang tidak menguntungkan "keterikatan kuantum." Faktanya, setiap evolusi sistem kuantum biasanya menghasilkan keterjeratan dari independensi (dan bukan sebaliknya), mengubah distribusi persegi panjang menjadi yang non-persegi panjang. Kemerdekaan itu langka dan sangat mudah dihancurkan.

Untuk lebih memahami dengan tepat apa yang menyebabkan proses fisik terjerat, kita mulai dengan sistem klasik. Gambar tersebut menunjukkan sistem bola cahaya bermuatan positif di jalur atas dan bola berat bermuatan negatif di jalur bawah. Awalnya, dua bola berjauhan dan hampir tidak berinteraksi. Kemudian kita turunkan jalur atas, menyatukan bola-bola sehingga mereka mulai menarik satu sama lain (muatan berlawanan ditarik). Dan bola cahaya menggelinding ke yang berat (dan bola yang berat menggelinding sedikit ke yang ringan, seperti apel yang jatuh menarik bumi sedikit ke dirinya sendiri).

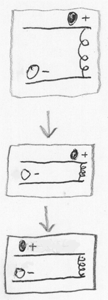
Sekarang mari kita lihat sistem ini sebagai sistem kuantum, dari sudut pandang integral jalur Feynman . Artinya, kami mewakili evolusi sistem sebagai jumlah dari semua lintasan yang mungkin dari keadaan awal di ruang konfigurasi. Misalkan dua bola awalnya kuantum independen, distribusi gabungan amplitudo dapat direpresentasikan sebagai produk "distribusi untuk bola yang lebih rendah" dan "distribusi untuk bola atas".

Selanjutnya, biarkan amplitudo bola bawah di awal terdiri dari tiga bagian (yang dari sudut pandang integral Feynman dapat dianggap sebagai tiga keadaan awal). Ketika kita menurunkan trek atas, bola atas harus ditarik ke bawah. Tetapi jika amplitudo sambungan bola bawah terdiri dari beberapa bagian, maka pada akhirnya kita akan mendapat distribusi sambungan yang terdiri dari beberapa bagian, yang masing-masing menggambarkan posisi bola yang baru.

Saya melakukan yang terbaik untuk menghindari kata-kata seperti "bola yang lebih rendah dapat berada di salah satu dari tiga tempat" atau "dalam setiap kasus yang mungkin, bola atas tertarik ke posisi yang sesuai dari yang lebih rendah". Meskipun Anda mungkin masih membayangkan semuanya seperti itu. Pada akhirnya, saya sendiri telah menggambarkan hal ini. Saya menggambar tiga posisi awal yang memungkinkan dan tiga kemungkinan hasil. Apa yang harus dilakukan, otak manusia biasanya membayangkan integral Feynman. Tetapi ini tidak berarti bahwa ada tiga kemungkinan keadaan alam semesta . Ini hanya trik untuk memvisualisasikan jalur yang tidak terpisahkan. Ketiga komponen amplitudo ada di alam semesta kita, ketiganya sama-sama nyata , tetapi sama sekali tidak mungkin atau tidak mungkin .

Sekarang bayangkan bahwa pada awalnya amplitudo bola yang lebih rendah "dioleskan" di seluruh trek. Amplitudo bola atas masih terkonsentrasi di satu tempat. Kemudian distribusi bersama awalnya akan dalam bentuk persegi panjang memanjang, dan kemudian berubah menjadi diagonal.

Pada sumbu X di sini adalah posisi bola atas, pada sumbu Y - bawah. Kami mulai dengan bola atas yang dilokalkan dengan tepat dan bola bawah yang "kabur" dan berakhir dengan distribusi yang saling tergantung ketika kedua koordinat kabur tetapi sama satu sama lain (disederhanakan). Yaitu, distribusi awalnya yang dapat diubah menjadi "sistem yang membingungkan" - tidak lagi terurai menjadi dua faktor independen.

(Pemberitahuan penting:

Perhatikan bahwa pada gambar di atas, pengembangan sistem mematuhi hukum termodinamika kedua , alias teorema Liouville. Ketika sistem berubah, "ukuran awan" dipertahankan, yaitu, volume total amplitudo, atau lebih sederhana, ukuran area abu-abu pada grafik . Jika pada awal gambar ada kotak abu-abu terang besar (ketika kedua partikel sangat dioleskan di ruang angkasa), maka menurut hukum kedua termodinamika, itu tidak bisa berubah menjadi diagonal abu-abu gelap. Untuk memasuki keadaan keterikatan, sistem awalnya harus memiliki entropi rendah, dan entropi ini seharusnya tidak meningkat banyak dalam proses.

Biarkan saya mengingatkan Anda bahwa informasi timbal balik adalah entropi dengan tanda sebaliknya . Amplitudo kuantum tidak sepenuhnya informasi , tetapi prinsipnya sama. Amplitudo awal harus cukup terkonsentrasi untuk menghasilkan garis diagonal yang ringkas, bukan awan yang besar dan jarang. Jika kita membayangkan bahwa distribusi amplitudo memiliki "entropi kuantum", maka entropi sistem yang terjerat seharusnya relatif rendah)

Akhirnya, kami siap berbicara tentang dekoherensi.

Sistem dalam gambar ini cukup rumit. Dapat digambarkan sesuatu seperti ini: "ada dua partikel, dan keduanya bisa ada di sini atau di sana ." Ya, saya merumuskannya seolah-olah ada dua kemungkinan keadaan, dan bukan distribusi amplitudo yang secara fisik nyata. Serius, saya tidak tahu cara menggambarkan fisika kuantum dalam bahasa biasa dengan cara yang normal! Ingat saja aturan umum bahwa "peluang" atau "probabilitas" adalah singkatan dari "bentangan distribusi amplitudo yang ada secara fisik". Kemudian saya bisa menggambarkan amplitudo jauh lebih pendek menggunakan ketentuan ketidakpastian. Tetapi ingat bahwa ini hanya sebuah konvensi ! "Sebuah partikel ada di sini atau di sana" berarti "distribusi amplitudo dua bagian yang ada secara fisik, satu di sini, satu di sana", dan bukan "partikel di salah satu dari dua tempat, tetapi kita tidak tahu yang mana".

Jadi Bekerja dengan sistem yang rumit biasanya sulit (bagi fisikawan, tentu saja, bukan untuk alam semesta). Pertama, kita harus menghitung semua lintasan yang mungkin untuk semua kondisi awal yang mungkin (yaitu, memperhitungkan semua lintasan amplitudo yang ada secara fisik di integral Feynman). Lebih lanjut, perlu untuk mempertimbangkan pengaruh lintasan ini pada satu sama lain ( kemungkinan lintasan dalam arti sempit tidak dapat berinteraksi - hanya sesuatu yang benar-benar ada yang dapat mempengaruhi hal lain). Sebagai contoh, dua partikel kita bertemu 20 lainnya, berinteraksi dalam beberapa cara, dan sebagai hasilnya kita mendapatkan banyak konfigurasi yang dipengaruhi oleh semua poin sebelumnya dari semua keadaan yang mungkin.

Perhatikan bahwa keterjeratan hanya terjadi jika bagian dari amplitudo awal dekat satu sama lain. Sehingga jalur pengembangan mereka bisa bersinggungan. Jika dua partikel ada di sini atau di sana , tetapi "di sini" dan "di sana" dipisahkan oleh jarak dua tahun cahaya, maka lintasan selanjutnya mereka dapat berpotongan tidak lebih awal dari setahun kemudian.

Sekarang tambahkan partikel ketiga . Gambar ini menunjukkan ruang konfigurasi tiga dimensi, yang terurai menjadi subruang dua dimensi dan satu dimensi yang independen. Yaitu, dua partikel terjerat dan satu terpisah dari mereka.

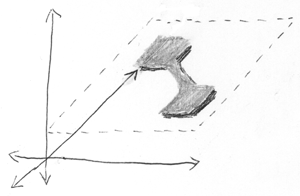
Tinggi adalah partikel ketiga, lebar dan kedalaman adalah dua partikel terjerat.

Partikel independen ada di tempat tertentu - distribusi vertikal sangat sempit. Dua partikel terjerat ada di sini atau di sana (saya kembali menggunakan istilah probabilistik yang salah, seperti "spesifik" dan "baik", tetapi Anda mengerti apa yang saya maksud).

Bayangkan sekarang bahwa partikel ketiga bereaksi dengan dua yang terjerat dengan cara yang peka terhadap posisi mereka. Sebagai contoh, partikel ketiga menyeimbangkan pada puncak yang tajam, dua partikel melintas, menariknya, dan jatuh ke satu arah atau lainnya. Setelah itu, amplitudo terlihat seperti ini.

Partikel ketiga sekarang bingung dengan dua lainnya. Dan amplitudo sekarang terdiri dari dua bagian yang terpisah satu sama lain . Deskripsi yang disederhanakan: “jika dua partikel ada di sini , maka partikel ketiga terbang di sini . Dan jika mereka ada di sana , maka dia terbang ke sana . " Artinya, amplitudo menjadi benar-benar bingung. Itu tidak lagi terurai menjadi ruang bagian independen.

Tetapi dua potong amplitudo sekarang terpisah lebih jauh , dan masing-masing terdiri dari tiga partikel di wilayah yang bersesuaian. Ini terjadi karena partikel ketiga peka terhadap koordinat yang lain. Setelah bergulir dari puncak yang tajam ke salah satu dari dua sisi, jarak antara koordinat akhir cukup besar.

Sebenarnya, bergulir turun dari atas adalah opsional. Semuanya bekerja dengan cara yang sama jika Anda memiliki dua puluh partikel yang bereaksi terhadap dua partikel pertama dan menjadi bingung dengan mereka. Distribusi akhir dalam ruang 22 dimensi akan terlihat seperti dua area, yang masing-masing sesuai dengan 22 partikel. Dan jarak antara area-area ini akan sangat besar. Dan semakin besar jarak, semakin kecil kemungkinan daerah di masa depan akan saling mempengaruhi.
Ini adalah dekoherensi. Ini adalah penyebab ketiga “halusinasi klasik,” karena kedua area mulai berkembang secara independen. Ini memungkinkan mereka untuk digambarkan sebagai sistem yang tidak rumit. Segera setelah kami mempertimbangkannya secara terpisah, distribusi di masing-masing terlihat "persegi panjang" dan secara independen dalam tiga koordinat (saya mencoba menunjukkan ini pada gambar di atas).

Dalam komputer kuantum, sangat sulit untuk mencegah dekoherensi. Komputasi kuantum mensyaratkan bahwa bagian amplitudo tetap dekat satu sama lain dan dapat berinteraksi. Tetapi ada triliunan partikel lain di sekitarnya yang terus-menerus berusaha bereaksi secara tidak sengaja dengan qubit rapuh kami, menghancurkan amplitudo yang dibangun dengan tepat.

Dan Anda tidak bisa hanya mengambil dan mengembalikan yang hancur. Untuk melakukan ini, perlu untuk kembali ke tempat semua partikel yang bereaksi, termasuk partikel acak dari lingkungan (jangan lupa, amplitudo akhir memiliki distribusi bersama dengannya).

(Kelihatannya seperti proses yang hampir tidak dapat diubah, kan? Ini seperti mencoba mengumpulkan telur yang pecah kembali ke kulitnya. Sebenarnya, ini analogi yang bagus.

Itulah sebabnya saya tekankan sebelumnya bahwa proses keterikatan dimulai dengan entropi rendah. Decoherence bersifat ireversibel karena pada dasarnya merupakan proses termodinamika.

Salah satu prinsip fisik dasar menyatakan bahwa Anda dapat "memutar kembali film" tanpa melanggar hukum dasar. Jika Anda memfilmkan sebutir telur jatuh di lantai lalu menggulungnya ke belakang, sehingga telur yang pecah terbang dari lantai, berkumpul kembali menjadi cangkang halus, Anda tidak akan melihat ada hukum fisika yang dilanggar. Semua molekul hanya akan berada di tempat yang tepat pada waktu yang tepat, dan telur akan terpental aman dan sehat. Ini bukan tidak mungkin, hanya sangat tidak mungkin.

Hal yang sama berlaku untuk amplitudo yang dipecah menjadi bagian-bagian yang jauh, tiba-tiba kembali ke keadaan koheren - ini secara teori dimungkinkan. Tapi praktis tidak ada kemungkinan bahwa potongan-potongan yang awalnya terputus tiba-tiba akan bersamaan di samping satu sama lain. Proses sebaliknya jauh lebih mungkin.

Bahkan, selain menggulung film kembali, Anda juga perlu membalik muatan semua partikel, serta menukar kiri dan kanan (atau salah satu dari dua dimensi lainnya), mengubah alam semesta menjadi gambar cermin dari itu. Aturan ini dikenal sebagai "invarian CPT" dari kata Mengisi, Paritas, dan Waktu.

Kemungkinan besar, invarian CPT adalah salah satu prinsip paling dasar dari berfungsinya alam semesta. Bagi fisikawan, upaya untuk mematahkannya tampak hampir absurd seperti mencoba melempar bola lebih cepat daripada kecepatan cahaya. Sejauh yang saya tahu, invariansi CPT diperlukan untuk konsistensi Teori Bidang Quantum.

Oleh karena itu, dekoherensi hanya tampak seperti proses searah, tetapi sebenarnya tidak dapat dibalikkan adalah termodinamika, bukan fundamental. Dan ini sangat penting, karena dari sini fisika kuantum mengamati invarian CPT.

Sejauh yang kita tahu, benar-benar semua proses searah di alam adalah konsekuensi dari hukum kedua termodinamika, dan bukan asimetri waktu yang mendasar.)

Untuk meringkas. Decoherence adalah proses termodinamika keterikatan kuantum yang terus meningkat, yang secara mengejutkan disamarkan sebagai proses menghancurkan keterikatan ini sendiri. Daerah yang asri tidak saling berinteraksi, dan masing-masing menjadi kurang membingungkan . Decoherence adalah alasan ketiga untuk "halusinasi klasik." Ini memungkinkan fisikawan untuk menganggap setiap bidang sebagai independen, tanpa memperhitungkan kemungkinan interaksi mereka yang kecil. Selain itu, setiap area individu menjadi lebih mudah dipahami di dalam . Ini sangat berguna jika Anda ingin menyelesaikan masalah dalam hal fisika klasik sederhana. Dan itu sangat tidak pantas jika Anda ingin memperhitungkan satu juta angka sebelum matahari terbenam.