Halo teman-teman. Kursus
Algoritma untuk Pengembang dimulai besok, dan kami masih memiliki satu terjemahan yang tidak diterbitkan. Sebenarnya kami memperbaiki dan berbagi materi dengan Anda. Ayo pergi.
Fast Fourier Transform (FFT) adalah salah satu algoritma pemrosesan sinyal dan analisis data yang paling penting. Saya menggunakannya selama bertahun-tahun tanpa pengetahuan formal dalam ilmu komputer. Tapi minggu ini terpikir oleh saya bahwa saya tidak pernah bertanya-tanya bagaimana FFT menghitung transformasi Fourier diskrit begitu cepat. Saya menyingkirkan debu dari sebuah buku tua tentang algoritma, membukanya, dan membaca dengan senang hati trik komputasi yang tampak sederhana yang dijelaskan oleh J.V. Cooley dan John Tukey dalam
karya klasik
1965 mereka tentang topik ini.
Tujuan dari posting ini adalah untuk terjun ke dalam algoritma FFT Cooley-Tukey, menjelaskan simetri yang mengarah padanya, dan menunjukkan beberapa implementasi Python sederhana yang menerapkan teori dalam praktek. Saya berharap bahwa penelitian ini akan memberikan spesialis analisis data, seperti saya, gambaran yang lebih lengkap tentang apa yang terjadi di bawah kap algoritma yang kami gunakan.
Discrete Fourier TransformFFT cepat
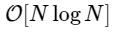
sebuah algoritma untuk menghitung transformasi Fourier diskrit (DFT), yang dihitung secara langsung untuk
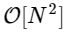
. DFT, seperti versi berkelanjutan dari transformasi Fourier yang lebih akrab, memiliki bentuk langsung dan terbalik, yang didefinisikan sebagai berikut:
Direct Discrete Fourier Transform (DFT):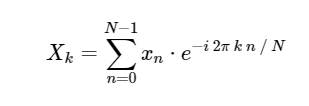
Invers Discrete Fourier Transform (ODPF):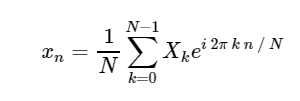
Konversi dari
xn → Xk adalah terjemahan dari ruang konfigurasi ke ruang frekuensi dan dapat sangat berguna untuk mempelajari spektrum daya sinyal dan untuk mengkonversi tugas-tugas tertentu untuk perhitungan yang lebih efisien. Anda dapat menemukan beberapa contoh dari tindakan ini di
bab 10 buku masa depan kami tentang astronomi dan statistik, di mana Anda juga dapat menemukan gambar dan kode sumber Python. Untuk contoh menggunakan FFT untuk menyederhanakan integrasi persamaan diferensial yang rumit, lihat posting saya
"Memecahkan persamaan Schrödinger dengan Python" .
Karena pentingnya FFT (selanjutnya FFT setara - Fast Fourier Transform dapat digunakan) di banyak area Python berisi banyak alat standar dan cangkang untuk menghitungnya. Baik NumPy dan SciPy memiliki cangkang dari pustaka FFTPACK yang teruji sangat baik, yang masing-masing terletak di
scipy.fftpack dan
scipy.fftpack . FFT tercepat yang saya tahu adalah dalam paket
FFTW , yang juga tersedia dalam Python melalui paket
PyFFTW .
Untuk saat ini, mari kita tinggalkan implementasi ini dan bertanya-tanya bagaimana kita dapat menghitung FFT dengan Python dari awal.
Perhitungan Transformasi Fourier DiskritUntuk kesederhanaan, kami hanya akan berurusan dengan konversi langsung, karena transformasi terbalik dapat diimplementasikan dengan cara yang sangat mirip. Melihat ekspresi DFT di atas, kita melihat bahwa ini tidak lebih dari operasi linear langsung: mengalikan matriks dengan vektor
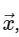
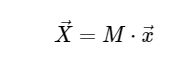
dengan matriks M diberikan
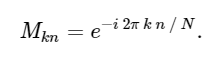
Dengan mengingat hal ini, kita dapat menghitung DFT menggunakan perkalian matriks sederhana sebagai berikut:
Dalam [1]:
import numpy as np def DFT_slow(x): """Compute the discrete Fourier Transform of the 1D array x""" x = np.asarray(x, dtype=float) N = x.shape[0] n = np.arange(N) k = n.reshape((N, 1)) M = np.exp(-2j * np.pi * k * n / N) return np.dot(M, x)
Kami dapat memeriksa hasilnya dengan membandingkannya dengan fungsi FFT yang dibangun di numpy:
Dalam [2]:
x = np.random.random(1024) np.allclose(DFT_slow(x), np.fft.fft(x))
0ut [2]:
TrueHanya untuk mengkonfirmasi lambatnya algoritme kami, kami dapat membandingkan waktu eksekusi dari dua pendekatan ini:
Dalam [3]:
%timeit DFT_slow(x) %timeit np.fft.fft(x)
10 loops, best of 3: 75.4 ms per loop 10000 loops, best of 3: 25.5 µs per loop
Kami lebih dari 1000 kali lebih lambat, yang diharapkan untuk implementasi yang disederhanakan. Tapi ini bukan yang terburuk. Untuk vektor input dengan panjang N, algoritma FFT berskala sebagai
sedangkan algoritma lambat kami seperti skala
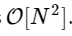
. Ini berarti untuk
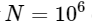
elemen, kami berharap FFT selesai dalam waktu sekitar 50 ms, sementara algoritma lambat kami akan memakan waktu sekitar 20 jam!
Jadi bagaimana FFT mencapai akselerasi seperti itu? Jawabannya adalah menggunakan simetri.
Simetri dalam transformasi Fourier diskritSalah satu alat paling penting dalam membangun algoritma adalah penggunaan simetri tugas. Jika Anda dapat menunjukkan secara analitis bahwa satu bagian dari masalah hanya terkait dengan yang lain, Anda dapat menghitung hanya hasil satu kali dan menghemat biaya komputasi ini. Cooley dan Tukey menggunakan pendekatan ini untuk mendapatkan FFT.
Kita mulai dengan pertanyaan tentang makna
. Dari ungkapan kami di atas:
di mana kami menggunakan exp identitas [2π dalam] = 1, yang berlaku untuk bilangan bulat apa pun n.
Baris terakhir menunjukkan dengan baik properti simetri DFT:
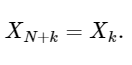
Ekstensi sederhana
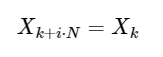
untuk bilangan bulat apa pun i. Seperti yang akan kita lihat di bawah, simetri ini dapat digunakan untuk menghitung DFT lebih cepat.
DFT di FFT: menggunakan simetriCooley dan Tukey menunjukkan bahwa perhitungan FFT dapat dibagi menjadi dua bagian yang lebih kecil. Dari definisi DFT kami memiliki:
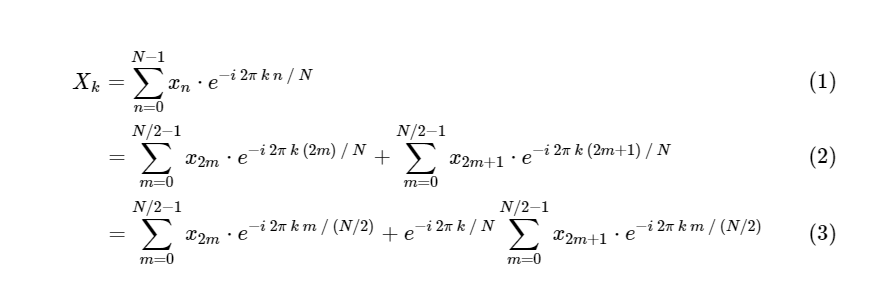
Kami membagi satu transformasi Fourier diskrit menjadi dua istilah, yang dalam dirinya sendiri sangat mirip dengan transformasi Fourier diskrit yang lebih kecil, satu untuk nilai dengan angka ganjil dan satu untuk nilai dengan angka genap. Namun, sejauh ini kami belum menyimpan siklus komputasi apa pun. Setiap istilah terdiri dari (N / 2) ∗ N perhitungan, total
.
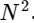
Caranya adalah dengan menggunakan simetri di setiap kondisi ini. Karena rentang k adalah 0≤k <N, dan kisaran n adalah 0≤n <M≡N / 2, kita melihat dari properti simetri di atas bahwa kita perlu melakukan hanya setengah perhitungan untuk setiap subtugas. Perhitungan kami
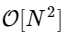
telah menjadi
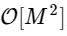
di mana M dua kali lebih kecil dari N.
Tetapi tidak ada alasan untuk memikirkan hal ini: selama transformasi Fourier kami yang lebih kecil memiliki M yang genap, kami dapat menerapkan kembali pendekatan pembagian dan menaklukkan ini, setiap kali mengurangi separuh biaya komputasi, sampai array kami cukup kecil sehingga strategi tidak lagi menguntungkan. Dalam batas asimptotik, pendekatan rekursif ini berskala sebagai O [NlogN].
Algoritma rekursif ini dapat diimplementasikan dengan sangat cepat dalam Python, mulai dari kode DFT kami yang lambat, ketika ukuran subtugas menjadi sangat kecil:
Dalam [4]:
def FFT(x): """A recursive implementation of the 1D Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if N % 2 > 0: raise ValueError("size of x must be a power of 2") elif N <= 32:
Di sini kita akan melakukan pemeriksaan cepat bahwa algoritma kami memberikan hasil yang benar:
Dalam [5]:
x = np.random.random(1024) np.allclose(FFT(x), np.fft.fft(x))
Keluar [5]:
TrueBandingkan algoritma ini dengan versi lambat kami:
-Dalam [6]:
%timeit DFT_slow(x) %timeit FFT(x) %timeit np.fft.fft(x)
10 loops, best of 3: 77.6 ms per loop 100 loops, best of 3: 4.07 ms per loop 10000 loops, best of 3: 24.7 µs per loop
Perhitungan kami lebih cepat daripada versi langsung! Selain itu, algoritma rekursif kami asimtotik
: kami menerapkan transformasi Fourier cepat.
Perhatikan bahwa kita masih tidak dekat dengan kecepatan algoritma FFT built-in numpy, dan ini harus diharapkan. Algoritma FFTPACK di belakang
fft numpy adalah implementasi Fortran yang telah menerima perbaikan dan optimasi selama bertahun-tahun. Selain itu, solusi NumPy kami mencakup rekursi tumpukan Python dan alokasi banyak array sementara, yang meningkatkan waktu komputasi.
Strategi yang baik untuk mempercepat kode ketika bekerja dengan Python / NumPy adalah membuat vektor kalkulasi berulang jika memungkinkan. Kita bisa melakukan ini - dalam prosesnya, hapus panggilan fungsi rekursif kami, yang akan membuat FFT Python kami semakin efisien.
Versi Numpy VektorHarap dicatat bahwa dalam penerapan FFT rekursif di atas, pada tingkat rekursi terendah, kami melakukan produk vektor-matriks identik
N / 32 . Efektivitas algoritma kami akan menang jika kami secara bersamaan menghitung produk-produk matriks-vektor ini sebagai produk matriks-matriks tunggal. Pada setiap tingkat rekursi berikutnya, kami juga melakukan operasi berulang yang dapat di-vektor. NumPy melakukan pekerjaan yang sangat baik untuk operasi semacam itu, dan kita dapat menggunakan fakta ini untuk membuat versi vektor dari transformasi Fourier cepat ini:
Dalam [7]:
def FFT_vectorized(x): """A vectorized, non-recursive version of the Cooley-Tukey FFT""" x = np.asarray(x, dtype=float) N = x.shape[0] if np.log2(N) % 1 > 0: raise ValueError("size of x must be a power of 2")
Meskipun algoritmanya sedikit lebih buram, itu hanyalah penataan ulang operasi yang digunakan dalam versi rekursif, dengan satu pengecualian: kami menggunakan simetri dalam perhitungan koefisien dan membangun hanya setengah dari array. Sekali lagi, kami mengkonfirmasi bahwa fungsi kami memberikan hasil yang benar:
Dalam [8]:
x = np.random.random(1024) np.allclose(FFT_vectorized(x), np.fft.fft(x))
Keluar [8]:
TrueKarena algoritme kami menjadi jauh lebih efisien, kami dapat menggunakan array yang lebih besar untuk membandingkan waktu, meninggalkan
DFT_slow :
Dalam [9]:
x = np.random.random(1024 * 16) %timeit FFT(x) %timeit FFT_vectorized(x) %timeit np.fft.fft(x)
10 loops, best of 3: 72.8 ms per loop 100 loops, best of 3: 4.11 ms per loop 1000 loops, best of 3: 505 µs per loop
Kami telah meningkatkan implementasi kami dengan urutan besarnya! Sekarang kita berada sekitar 10 kali dari patokan FFTPACK, hanya menggunakan beberapa lusin baris Python + NumPy murni. Meskipun ini masih belum konsisten secara komputasi, dalam hal keterbacaan, versi Python jauh lebih unggul dari kode sumber FFTPACK, yang dapat Anda lihat di
sini .
Jadi bagaimana FFTPACK mencapai akselerasi terakhir ini? Yah, pada dasarnya, ini hanya masalah pembukuan yang terperinci. FFTPACK menghabiskan banyak waktu untuk menggunakan kembali kalkulasi antara yang dapat digunakan kembali. Versi kasar kami masih mencakup alokasi memori berlebihan dan penyalinan; dalam bahasa tingkat rendah seperti Fortran, lebih mudah untuk mengontrol dan meminimalkan penggunaan memori. Selain itu, algoritma Cooley-Tukey dapat diperluas untuk menggunakan partisi dengan ukuran selain 2 (apa yang telah kami terapkan di sini dikenal sebagai Cooley-Tukey Radix FFT berdasarkan 2). Algoritma FFT lain yang lebih kompleks juga dapat digunakan, termasuk pendekatan yang berbeda secara mendasar berdasarkan data konvolusi (lihat, misalnya, algoritma Blueshtein dan algoritma Raider). Kombinasi dari ekstensi dan metode di atas dapat menyebabkan FFT yang sangat cepat bahkan pada array yang ukurannya bukan kekuatan dua.
Meskipun fungsi dalam Python murni mungkin tidak berguna dalam praktiknya, saya berharap mereka memberikan beberapa wawasan tentang apa yang terjadi di latar belakang analisis data berbasis FFT. Sebagai ahli data, kita dapat mengatasi implementasi "kotak hitam" dari alat fundamental yang dibuat oleh kolega kita yang lebih berpikiran algoritmik, tetapi saya yakin bahwa semakin banyak pemahaman yang kita miliki tentang algoritma tingkat rendah yang kita terapkan pada data kita, praktik yang lebih baik kami akan.
Posting ini ditulis seluruhnya dalam Notepad IPython. Notebook lengkap dapat diunduh di
sini atau dilihat secara statis di
sini .
Banyak yang mungkin memperhatikan bahwa materi itu jauh dari baru, tetapi, seperti yang terlihat bagi kita, cukup relevan. Secara umum, tulis apakah artikel itu bermanfaat. Menunggu komentar Anda.