Duo matematika memetakan wilayah permukaan minimal yang tak berujung

Beberapa ahli matematika berdasarkan teori matematika yang kurang dikenal 30 tahun yang lalu menunjukkan bahwa permukaan minimal yang menyerupai film sabun muncul dalam jumlah besar pada berbagai macam angka.

Pada akhir 2011, Brian White sesekali mendengar ketukan di pintu kantor Stanford-nya. Di luar, pada saat-saat ini, dua matematikawan muda menunggunya, Fernando Coda Marquez dan Andre Nevis , yang selalu memiliki pertanyaan yang sama: apakah White punya waktu beberapa menit untuk membantu mereka mencari tahu salah satu bagian tak dikenal dari disertasi yang tidak diketahui untuk beberapa ratus halaman yang ditulis tiga puluh tahun yang lalu?

Disertasi, yang ditulis oleh John Pitts , menyajikan mekanisme yang kuat untuk membangun permukaan minimal - struktur yang mirip dengan film dan gelembung sabun - dalam berbagai bentuk. Ketika permukaan minimal dapat dibangun pada gambar, yang terakhir memungkinkan untuk mempelajari geometri ruang di sekitarnya. Permukaan seperti itu muncul dalam berbagai masalah ilmiah, dari studi lubang hitam hingga pengembangan biomolekul.

Namun, selama bertahun-tahun ini, disertasi Pitts telah berada di luar perhatian para sarjana - mungkin karena itu sangat sulit dibaca. Marquez dan Nevis yakin bahwa ada potensi besar di dalamnya. "Jelas bagi kami bahwa teori ini sepenuhnya diremehkan dan tidak diperhatikan," kata Nevis, yang sekarang menjadi profesor di University of Chicago.

Meskipun White tidak pernah bertanya kepada pasangan itu mengapa mereka tertarik pada pekerjaan Pitts, mereka setiap kali menyatakan bahwa minat mereka “murni bersifat akademis,” kata Nevis. Namun, mereka memiliki tujuan yang pasti - untuk membuktikan hipotesis Wilmore 50 tahun yang lalu, yang membahas masalah menemukan bentuk donat terbaik (detail nanti). Setelah tiga bulan berjuang dengan ide-ide dari disertasi Pitts, Marquez dan Nevis mencapai tujuan mereka , mendapatkan banyak penghargaan dan ulasan positif.

Tetapi dalam beberapa tahun terakhir, mereka telah mampu mendorong gagasan Pitts lebih jauh. Pitts, dengan kuratornya, Frederick Almgren, menemukan cara untuk memastikan bahwa setiap figur dalam sejumlah kecil dimensi memiliki setidaknya satu permukaan minimum. Sekarang, Marquez dan Nevis, menggunakan kohort matematikawan muda yang berkumpul di sekitar mereka, berdasarkan ide-ide Almgren dan Pitts, telah menunjukkan bahwa dalam kasus umum bentuk-bentuk ini harus mengandung banyak permukaan minimal - banyak permukaan berkerumun dan berkerumun di semua sudut angka. "Ini adalah terobosan besar," geometer terkenal Karen Uhlenbeck dari University of Texas menulis kepada kami melalui email.

"Dibutuhkan banyak upaya untuk membuat permukaan minimal tunggal," kata Richard Shoin dari University of California, Irvine, yang memberi tahu Nevis sekitar 15 tahun yang lalu. "Fakta bahwa ada begitu banyak dari mereka yang menakjubkan."

Kebangkitan teori Almgren dan Pitts ini telah menyebabkan ledakan aktivitas dalam beberapa tahun terakhir. "Hasilnya sangat cepat dan dalam jumlah besar sehingga sulit untuk melacaknya," kata White. "Tampaknya sangat menarik dan luar biasa bagi saya."

Menandai barisan gunung

Celupkan kawat melengkung ke dalam larutan sabun, atau tiupkan gelembung sabun, dan cairan itu akan dengan cepat membentuk permukaan area sekecil mungkin. Geometri dari permukaan minimal ini telah ditempati matematikawan selama ratusan tahun. Mereka muncul di berbagai bidang, dari arsitektur, di mana permukaan minimal menginspirasi desain atap dan struktur lainnya, hingga pembuatan partikel mikro untuk pengiriman obat. Lima tahun yang lalu, ketika sebuah tim ilmuwan menciptakan molekul berpori yang mampu membawa obat atau hormon di dalam diri mereka, mereka menemukan bahwa beberapa molekul mengambil bentuk gyroid , permukaan berulang tanpa akhir, yang sebagian menyerupai film sabun.

Secara teknis, matematikawan hanya menganggap film sabun pada kawat sebagai permukaan dengan permukaan minimum, tetapi bukan gelembung sabun, karena dalam ruang abstrak di mana tidak ada molekul udara, gelembung akan mengempis ke suatu titik. Namun, film di atas kawat tidak sepenuhnya memuaskan ahli matematika. Bagian dalamnya adalah permukaan yang halus, tetapi kawatnya putus dengan tajam. Adalah logis untuk berpikir tentang apakah mungkin untuk memperluas permukaan ini di luar batas batas kawat sehingga terus terlihat seperti film sabun di setiap area individu. Terkadang ini mungkin, dan permukaan membentang hingga tak terbatas. Terkadang permukaan kembali dan canggung bersinggungan dengan dirinya sendiri, atau menemui kesulitan lain.


Gyroid - jenis permukaan minimum yang terjadi selama desain mikropartikel untuk pengiriman obat

Di ruang biasa, ini melelahkan semua kemungkinan. Tetapi matematikawan dan ilmuwan lain sering menganggap dunia lain yang berbeda dari ruang tiga dimensi yang tak terbatas yang biasa kita gunakan - melengkung atau terbatas, seperti analogi tiga dimensi dari bola atau permukaan torus. Figur seperti itu memiliki kemungkinan baru yang menarik: permukaan minimal yang menekuk pada diri mereka sendiri dan mengunci ke angka akhir yang tertutup yang tidak memerlukan dukungan kawat.

Dalam teori relativitas, permukaan minimal hingga ini memainkan peran horizon peristiwa lubang hitam. Dan jika mereka dapat ditemukan pada gambar apa pun, ini membantu matematikawan untuk mempertimbangkan geometri mereka dari sisi yang berbeda: mereka memberikan template untuk memotong gambar (atau bermacam - macam ) menjadi potongan-potongan yang berpotensi lebih sederhana, mereka menunjukkan area kelengkungan positif di dalam manifold - menjadi beberapa bagian, melengkung ke dalam, seperti bola atau lubang hitam, sebagai lawan melengkung ke luar.

“Kami tahu sedikit tentang manifold dengan kelengkungan positif,” kata Shoin.

Namun, seringkali sulit untuk membuktikan keberadaan permukaan minimal dalam sebuah gambar. Untuk memahami mengapa demikian, pertimbangkan versi dua dimensi dari masalah ini. Pertanyaan menemukan permukaan minimum masuk akal dalam dimensi apa pun: matematikawan hanya menganggap permukaan sebagai bentuk yang dimensinya kurang dari ruang di mana ia hidup. Jadi dalam dunia dua dimensi, kurva "geodesik" yang terdiri dari jalur terpendek yang menghubungkan titik-titik terdekat adalah permukaan minimum.

Untuk beberapa angka dua dimensi, mudah menemukan kurva geodesik tertutup dalam loop terbatas. Ambil permukaan torus - bahkan tidak harus genap dan simetris, biarkan memiliki penyimpangan dan tonjolan. Jika kita membungkus donat dengan pita elastis yang melewati bagian tengahnya, kita dapat membayangkan bagaimana kita mengencangkannya dan menggesernya ke berbagai posisi yang memungkinkan. Salah satunya akan menjadi yang terpendek - itu akan menjadi kurva geodesik menurut definisi.



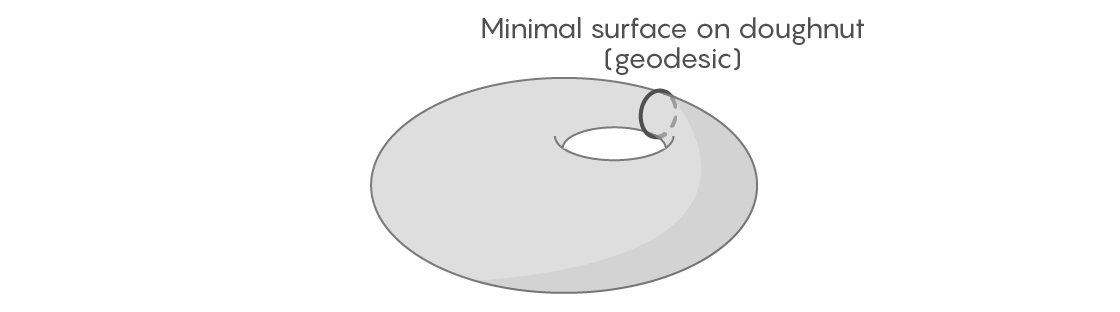
Tetapi jika bola adalah sosok kita, pendekatan ini tidak akan berfungsi lagi. Pada bidang datar sempurna, mudah untuk menemukan kurva geodesik - itu akan menjadi ekuator dan lingkaran penuh lainnya. Tetapi pada bidang yang tidak rata, misalnya, di permukaan bumi, tidak jelas ke mana kurva geodesik pergi dan apakah ada yang ditutup dalam satu lingkaran. Anda dapat membayangkan bagaimana kita membungkus bumi dengan pita elastis, seperti pada donat. Tetapi jika Anda mulai menggerakkannya, mencoba memendekkannya, ia akan menyusut ke satu titik, karena tidak seperti donat, bola tidak memiliki lubang untuk dilekatkan elastis.

Namun, kegagalan dengan pita elastis ini penuh dengan kuman kesuksesan. Jika khatulistiwa bola bundar dicegat oleh pita elastis, maka satu-satunya cara untuk menggesernya - untuk menambahkan gelombang ke dalamnya - akan membuatnya lebih lama. Jika Anda memindahkannya secara berbeda, naik atau turun ke garis lintang baru, garis itu akan menjadi lebih pendek. Oleh karena itu, garis khatulistiwa akan menjadi kurva terpendek dari satu sudut pandang, dan paling panjang dari yang lain.

Hal ini membuat garis khatulistiwa terkait dengan pelana melewati gunung, titik tertinggi di satu sisi (dari jalur melalui pegunungan) dan terendah di sisi lain (dari jalur ke puncak terdekat). Dan ini bukan hanya analogi yang lemah: sebagai aturan, permukaan minimal berubah menjadi pelana seperti itu, tetapi pegunungan mereka hidup di dunia yang jauh lebih sulit untuk divisualisasikan.



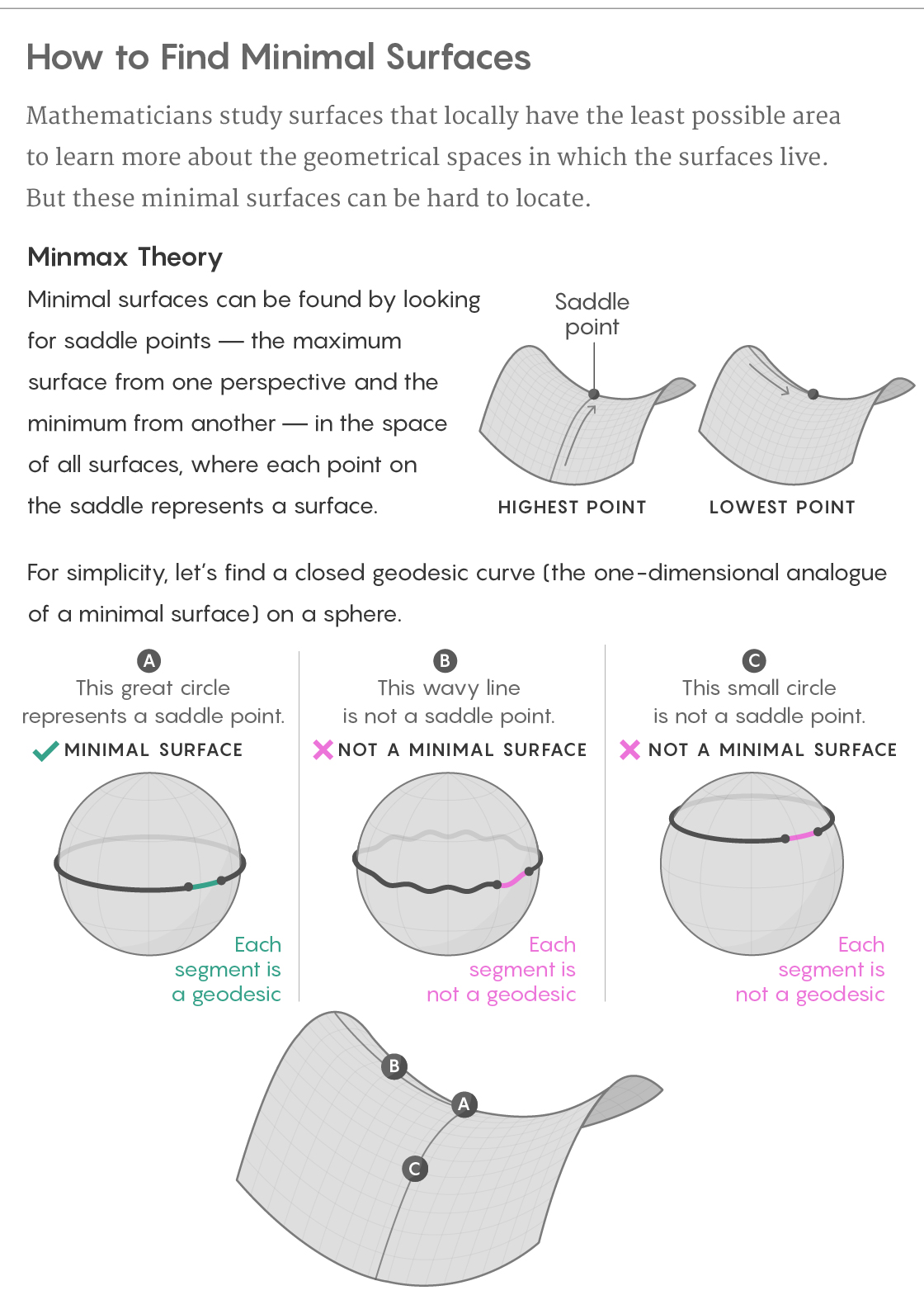
Menentukan permukaan minimum suatu gambar, kita dapat mempertimbangkan dunia baru yang terdiri dari semua kemungkinan permukaan terbatas yang ada di dalam gambar ini - kita akan menyebutnya "permukaan permukaan". Setiap titik ruang permukaan sesuai dengan seluruh permukaan seluruhnya pada gambar aslinya. Kemudian kita dapat mempertimbangkan luas setiap permukaan sebagai ketinggian titik yang sesuai dalam ruang permukaan, sebagai akibatnya dunia kita akan memiliki topografi alami. Pencarian untuk permukaan minimal pada gambar asli menjadi pencarian pelana di ruang permukaan.

Pada tahun 1917, George David Birkhoff menggunakan pendekatan ini untuk menunjukkan bahwa setiap bola, bergelombang atau halus, harus memiliki satu kurva geodesik tertutup. Sekitar enam dekade kemudian, Almgren dan Pitts dengan hebat mengembangkan gagasan Birkhoff dengan menandai topografi ruang permukaan ke semua angka hingga dalam dimensi dari tiga menjadi tujuh, dan kemudian menggunakan topografi ini untuk membuktikan bahwa angka-angka seperti itu selalu memiliki setidaknya satu permukaan minimal yang tertutup. Disertasi Pitts dari 1981 tentang teori Minmax ini - dinamakan demikian karena pelana adalah minimum dan maksimum - adalah "benar-benar menakjubkan," kata Nevis.

Namun, itu sangat kompleks. Hanya sedikit orang yang memahami nuansa teori, dan beberapa ahli matematika yang mempelajarinya mengklaim bahwa itu tidak sepenuhnya dikonfirmasi, kata Shoin. "Saya tidak berpikir ada keraguan bahwa itu sangat menarik dan penting," katanya. "Tapi tidak jelas seberapa penuh itu."

Bekerja pada teori Minmax secara bertahap menjadi sia-sia. "Pekerjaan Pitts telah dilupakan oleh komunitas matematika selama sekitar 30 tahun," kata Nevis. Dia tidak dibangkitkan sampai Nevis dan Marquez bertemu pada tahun 2006 di lift gedung matematika Universitas Princeton.

Di atas celah gunung

Pada saat itu, Marquez tiba di Princeton untuk memberikan kuliah; Nevis mendapat pekerjaan di sana tak lama setelah mempertahankan gelar doktor. Keduanya memiliki bahasa Portugis sebagai bahasa ibu mereka (Marquez berasal dari Brasil dan Nevis dari Portugal), dan mereka dengan mudah menemukan bahasa yang sama. "Lalu saya berbicara dengannya untuk pertama kalinya, tetapi dia berbicara dengan saya seolah-olah kami telah berteman selama 10 tahun," kenang Marquez, sekarang seorang profesor di Princeton.

Kemudian mereka menemukan bahwa mendiskusikan ide-ide matematika sama wajarnya bagi mereka. Mereka memiliki gaya yang berbeda: Marquez lebih tenang, dan Nevis lebih intens. Tapi ini menjadi nilai tambah bagi mereka. "Sangat jarang menemukan seseorang yang melengkapi Anda dengan sangat baik," kata Marquez.

Keduanya sangat ingin menemukan beberapa masalah matematika yang rumit yang bisa dibenamkan. Selama beberapa tahun, pasangan itu melontarkan gagasan setiap kali jalan mereka dilintasi untuk "melihat apa yang tertunda," kata Nevis. "Kami punya sejuta ide, dan sebagai hasilnya, salah satunya disaring dan berubah menjadi sesuatu yang terbentuk."

Masalah yang disaring ternyata adalah masalah yang terkenal dari "hipotesis Wilmore". Dia menyarankan menemukan bentuk torus yang meminimalkan besarnya yang dikenal sebagai energi Willmore, yang, secara kasar, mengukur perbedaan antara bentuk yang diberikan dan bola melingkar. Pada tahun 1965, Wilmore menyarankan bahwa itu akan menjadi donat paling bulat dari bentuk yang sangat simetris, yang dikenal sebagai torus Clifford , namun, meskipun banyak upaya, hipotesis ini tidak dapat dibuktikan kepada siapa pun.


Marquez (kiri) dan Nevis

Marquez dan Nevis mengembangkan pendekatan yang menjanjikan, tetapi agar berhasil, mereka membutuhkan bahan terakhir: teori minimax. Mereka berpikir bahwa menguasai teori ini dan menulis karya terakhir akan memakan waktu dua hingga tiga minggu - sampai mereka membuka buku Pitts. “Kami terkejut - ada apa ini? - kata Nevis. "Buku itu sangat kering."

Teorema yang terpisah tumbuh menjadi banyak halaman - dan ini hanya deskripsi dari teorema, bukan bukti mereka. Teorema utama sulit ditemukan. "Aku ingat bagaimana Fernando datang ke kantorku dan berkata: Aku menemukan pernyataan teorema!" - kata Nevis.


Thor Clifford

Ketika mereka terjebak, mereka bermain poker dan meminta bantuan White, salah satu dari sedikit orang yang mengerti sebagian besar pekerjaan Pitts (meskipun White sendiri menggambarkan percakapan ini sebagai "buta, memimpin buta"; Pitts sendiri, seorang profesor di A&M University of Texas, lulus menulis bekerja pada teori minmax beberapa dekade yang lalu). “Kami sangat termotivasi, sehingga kami dapat menerobos,” kenang Nevis. "Tapi itu bukan tugas untuk orang yang lemah hati."

Pada saat Marquez dan Nevis menyelesaikan bukti hipotesis Wilmore, mereka memahami teori Minmax lebih baik daripada ahli matematika lainnya. Mereka yakin bahwa potensinya meluas lebih jauh daripada pernyataan hipotesis itu sendiri. "Kami tahu kami memiliki teori yang sangat kuat," kata Nevis. - Setiap kali, menggunakan metode untuk membuktikan hasil tertentu yang tetap terbuka untuk waktu yang lama, Anda mengerti bahwa ada sesuatu di dalamnya. Ini menunjukkan bahwa perlu terus menggali lebih jauh. "

Diagram minmax dari Almgren dan Pitts menghasilkan tidak hanya satu sadel, tetapi jumlah mereka yang tak terbatas. Secara teori, ini harus sesuai dengan jumlah minimal permukaan minimal dari bentuk aslinya. Tetapi Almgren dan Pitts tidak dapat menunjukkan bahwa permukaan minimal yang diperoleh dengan cara ini berbeda. Oleh karena itu, satu-satunya hal yang pasti dapat dikatakan adalah bahwa setiap gambar memiliki setidaknya satu permukaan minimal.

Setelah itu, "pengembangan topik praktis berhenti," kata Nevis. "Itu adalah hasil terbaik untuk jangka waktu lebih dari 30 tahun."

Bahan baru diperlukan, dan Marquez dan Nevis menemukannya. Daftar permukaan minmax yang tak ada habisnya, seperti yang ditunjukkan pada tahun 2016, berperilaku sama dengan frekuensi drum.

Matematikawan German Weil pada tahun 1911 menunjukkan bahwa frekuensi dasar drum memiliki satu sifat yang tidak terduga: secara kasar, frekuensi tinggi hanya bergantung pada volume drum, dan bukan pada bentuknya. Marquez dan Nevis, bersama dengan Eugene Lekumovich dari Massachusetts Institute of Technology, menunjukkan bahwa permukaan Minmax memenuhi hukum matematika yang mirip dengan hukum frekuensi drum. Secara khusus, area permukaan secara kasar ditentukan oleh jumlah ruang di mana mereka hidup, dan bukan oleh bentuknya.

Hasil ini, yang mengakhiri hipotesis yang diajukan beberapa dekade lalu, memungkinkan Marquez dan Nevis tampil pada 2017 - kali ini mereka dibantu oleh Kay Air dari Universitas Tokyo - bahwa untuk sebagian besar daftar minmax berisi jumlah tak terbatas dari berbagai permukaan minimal yang berbeda. Selain itu, mereka menunjukkan bahwa permukaan ini "padat": mereka muncul di sebelah setiap titik di ruang sekitarnya. Intuisi yang mendukung kesimpulan ini adalah agar volume ruang untuk menentukan area lokasi permukaan minimal, yang terakhir harus entah bagaimana “melihat” seluruh volume. Dan ini "mengatakan bahwa orang-orang ini adalah semua keberagaman mereka," kata Marquez.

Beberapa bulan kemudian, pasangan ini, bersama dengan mahasiswa pascasarjana Marques Antoine Sun , menunjukkan bahwa jika Anda melihat daftar permukaan minmax, Anda akan melihat bahwa mereka memenuhi ruang secara merata - apa yang oleh para ahli matematika disebut " pemerataan " muncul.

"Ketika saya mendengar bahwa mereka didistribusikan secara merata, saya kagum," kata White. "Sepertinya orang seharusnya tidak dapat membuktikan hasil seperti itu selama hidupku."

Dalam beberapa tahun terakhir, beberapa matematikawan telah bergabung. Sebagai contoh, pada bulan Januari, Xin Zhou dari University of California di Santa Barbara, berdasarkan karya sebelumnya oleh Marquez dan Nevis, membuktikan bahwa untuk sebagian besar angka, semua permukaan minimal pada daftar Almgren dan Pitts berbeda satu sama lain, yang memberikan poin yang bagus tentang masalah ini. "Ini benar-benar menutup topik ini dengan baik, buka sejak zaman Almgren dan Pitts di tahun 80-an," kata White.

Keluarga hasil ini memperhitungkan hampir setiap angka dalam dimensi dari tiga hingga tujuh - dengan pengecualian bentuk yang paling halus, tidak peduli seberapa berlawanan dengan intuisi. Tetapi Juni lalu, Sunn mampu membuktikan bahwa setiap gambar dalam dimensi ini, termasuk yang paling bulat, memiliki banyak permukaan minimal tertutup, yang membenarkan hipotesis lain yang berusia beberapa dekade.

Masih belum jelas apakah kepadatan dan pemerataan akan berperilaku seragam, serta bagaimana teori minmax tidak bekerja dalam manifold kompak, atau dalam delapan dimensi atau lebih (namun, karya baru ini telah mencapai beberapa keberhasilan di sini juga). Matematikawan memperkirakan bahwa kita akan dapat menjawab banyak pertanyaan lebih cepat daripada kelihatannya.

"Semuanya berkembang sangat cepat," kata Nevis. "Setiap minggu saya melihat situs dengan cetakan arxiv, dan saya melihat di sana bagaimana seseorang memutuskan sesuatu yang lain."

Dari satu sudut pandang, karya-karya ini menandai akhir - atau akhir - dari sebuah kisah yang telah menggantung dalam keadaan yang belum selesai selama hampir empat dekade. Tetapi ini juga merupakan awal yang baru: matematikawan baru mulai memahami bahwa ide-ide baru mengenai permukaan minimal ini dapat memberi tahu kita tentang ruang tempat mereka tinggal.

"Saya bisa berasumsi bahwa cara-cara menarik lainnya untuk menerapkan pengetahuan ini akan segera muncul, tetapi apa sebenarnya, saya pasti tidak bisa mengatakannya," kata Shoin. "Saya yakin ini akan menjadi salah satu arah utama dalam geometri."