Geekly articles weekly

Tes numerik saya untuk hipotesis Tarif Absolut

Halo, Habr!

Publikasi ini sepertinya menarik bagi saya: Kami mendapatkan nilai tukar absolut dari nilai tukar lintas mata uang berpasangan dan saya ingin menguji kemampuan untuk menemukan nilai tukar aaaabsolute ini melalui pemodelan numerik, umumnya meninggalkan aljabar linear.



Hasilnya menarik.

Eksperimen akan menjadi kecil: 4 mata uang, 6 pasangan mata uang. Untuk setiap pasangan, satu pengukuran saja.

Jadi mari kita mulai


Hipotesisnya adalah bahwa nilai mata uang apa pun dapat dinyatakan sebagai nilai yang akan memperhitungkan nilai mata uang lain yang dikutipnya, sementara mata uang lain sendiri akan dinyatakan dalam nilai semua mata uang lainnya. Ini adalah tugas rekursif yang menarik.

Ada 4 mata uang:

  • usd
  • eur
  • chf
  • gbp

Bagi mereka, pasangan mata uang dipanggil:

  • Eurusd
  • gbpusd
  • Eurchf
  • Eurgbp
  • gbpchf
  • usdchf

Harap dicatat bahwa jika jumlah mata uang adalah n = 4, maka jumlah pasangan adalah k = (n ^ 2 - n) / 2 = 6. Tidak masuk akal untuk mencari pengguna jika eurusd dikutip ...

Pada waktu t, nilai tukar salah satu penyedia diukur:



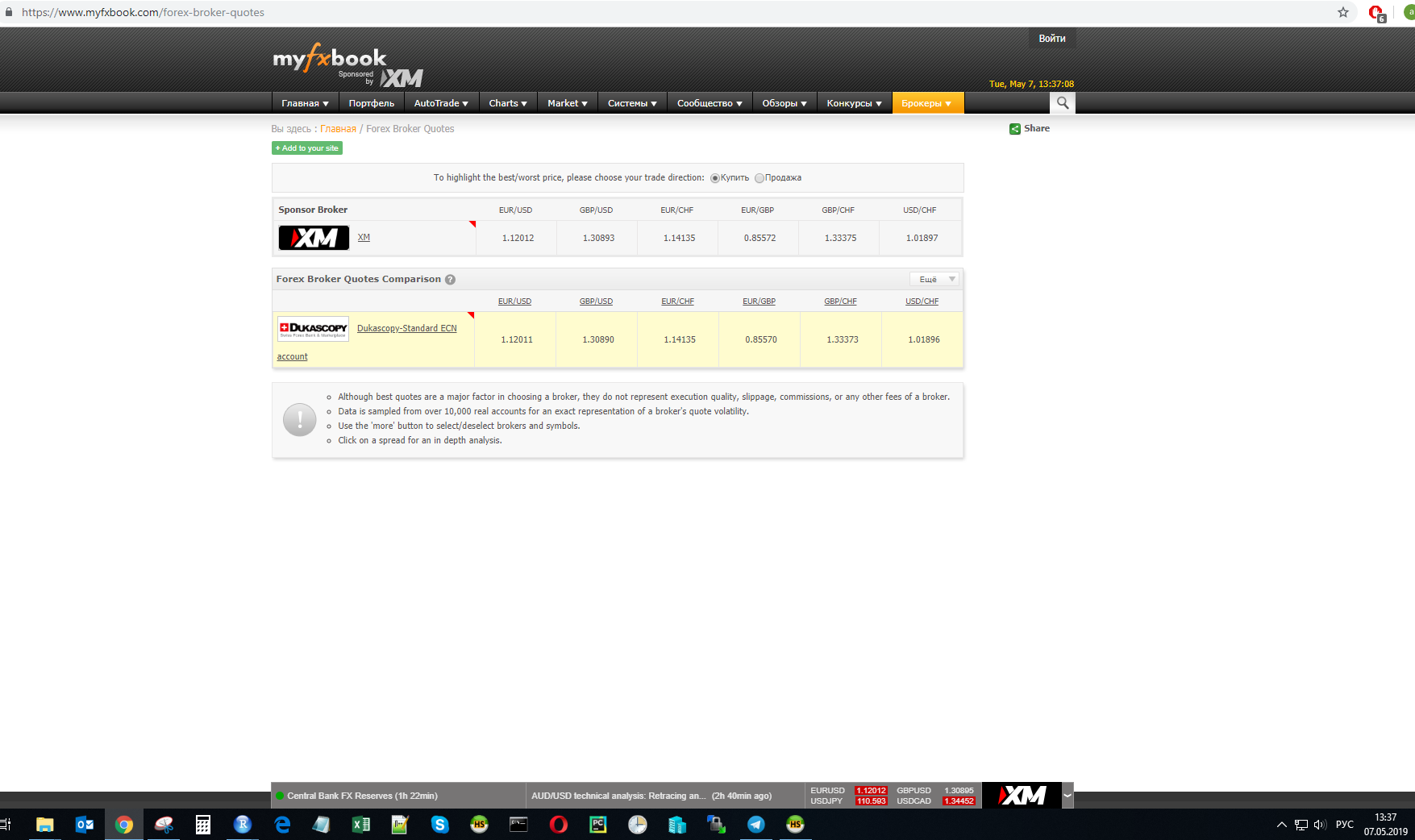
Perhitungan akan dilakukan untuk nilai-nilai ini.

Matematika


Saya memecahkan masalah dengan secara analitik mengambil gradien dari fungsi kerugian, yang pada dasarnya adalah sistem persamaan.

Kode percobaan akan berada di R:

#set.seed(111) usd <- runif(1) eur <- runif(1) chf <- runif(1) gbp <- runif(1) # snapshot of values at time t eurusd <- 1.12012 gbpusd <- 1.30890 eurchf <- 1.14135 eurgbp <- 0.85570 gbpchf <- 1.33373 usdchf <- 1.01896 ## symbolic task ------------ express <- expression( (eurusd - eur / usd) ^ 2 + (gbpusd - gbp / usd) ^ 2 + (eurchf - eur / chf) ^ 2 + (eurgbp - eur / gbp) ^ 2 + (gbpchf - gbp / chf) ^ 2 + (usdchf - usd / chf) ^ 2 ) eval(express) x = 'usd' D(express, x) eval(D(express, x))

R memungkinkan menggunakan stats :: D untuk mengambil turunan dari suatu fungsi. Misalnya, jika kita ingin membedakan dengan mata uang USD, kita mendapatkan ungkapan:
2 * (eur / usd ^ 2 * (eurusd - eur / usd)) + 2 * (gbp / usd ^ 2 * (gbpusd -
gbp / usd)) - 2 * (1 / chf * (usdchf - usd / chf))
Untuk mengurangi nilai fungsi express, kita akan melakukan gradient descent dan segera jelas (kita melihat perbedaan kuadrat) bahwa nilai minimum akan menjadi nol, yang merupakan apa yang kita butuhkan.

 -deriv_vals * lr

Langkah gradient descent akan dikontrol oleh parameter lr dan semua ini diambil dengan tanda negatif.

Artinya, dalam kata-kata manusia, kami memilih nilai mata uang 4 sehingga semua pasangan mata uang dalam percobaan menerima nilai yang sama dengan nilai awal dari pasangan ini. Mmm, mari kita pecahkan puzzle - di dahi!

Hasil


Agar tidak meregang, saya akan segera memberi tahu Anda hal berikut: percobaan secara keseluruhan berhasil, kode berfungsi, kesalahannya mendekati, mendekati nol. Tetapi kemudian saya perhatikan bahwa hasilnya selalu berbeda.

Sebuah pertanyaan untuk para pecinta: tampaknya tugas ini memiliki sejumlah solusi yang tidak terbatas, tetapi dalam hal ini saya benar-benar nol, saya pikir mereka akan memberi tahu saya di komentar.

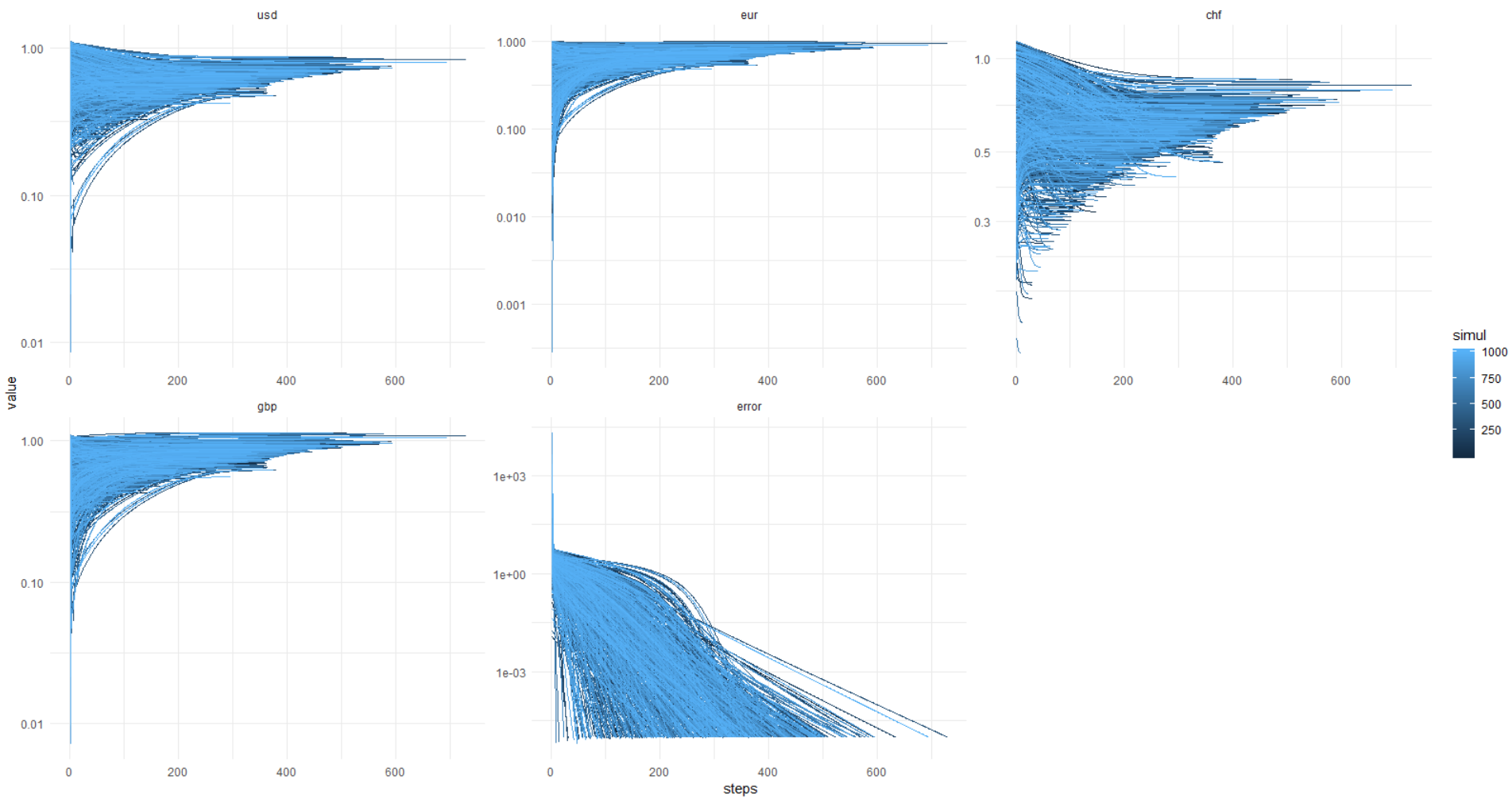
Untuk memverifikasi stabilitas (tidak) solusi, saya mensimulasikan 1000 kali tanpa memperbaiki seed PRNG untuk nilai awal dari nilai mata uang.

Dan inilah gambar dari kata: error mencapai 0,00001 dan kurang (optimasi diatur seperti ini) selalu, sementara nilai mata uang melayang iblis, tahu di mana. Ternyata selalu ada keputusan yang berbeda, tuan-tuan!

Sekali lagi, gambar ini, sumbu-y dalam unit asli (bukan log.):



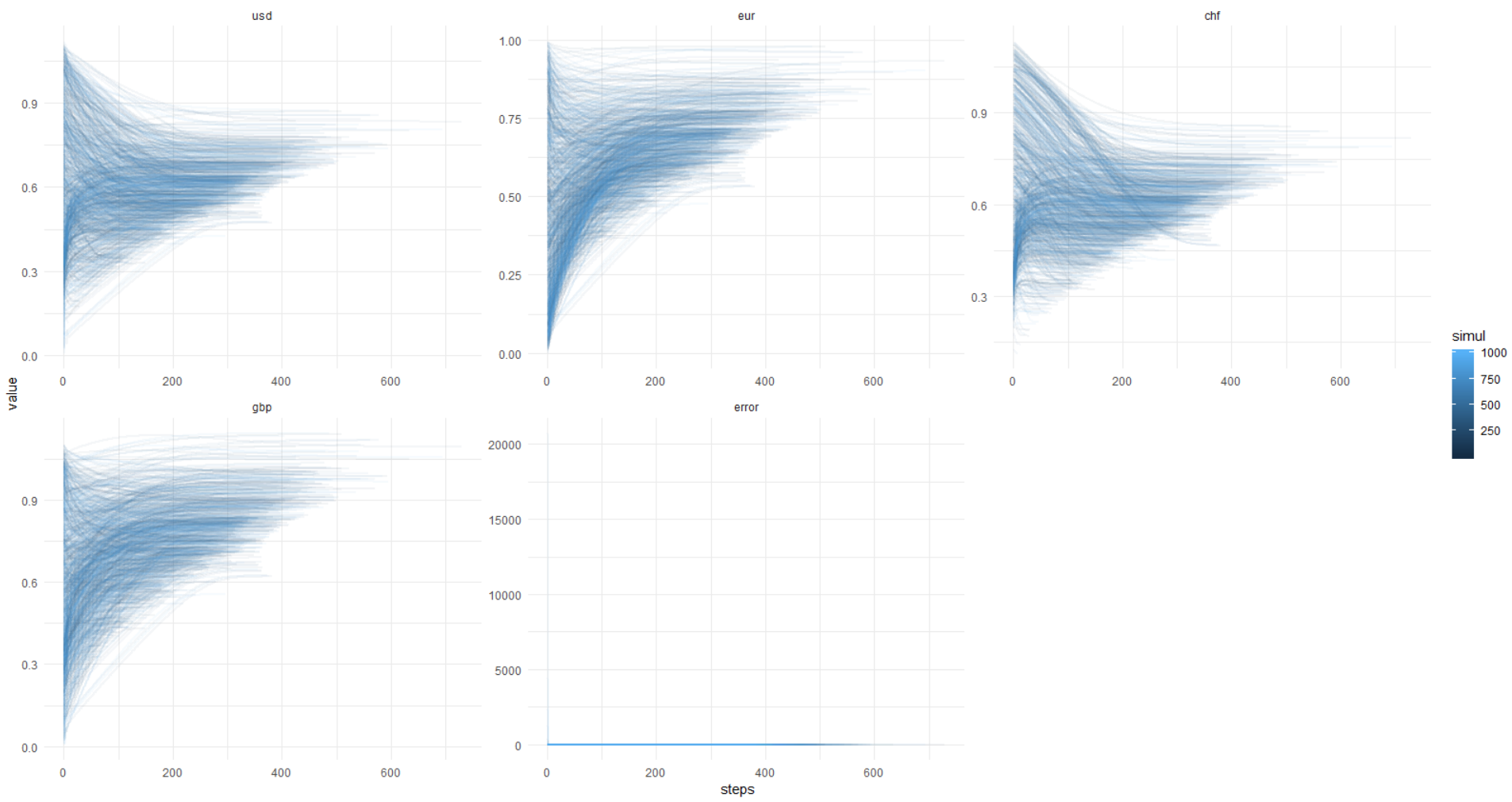
Agar Anda dapat mengulanginya, di bawah ini saya lampirkan kode lengkap.

Kode
 # clear environment rm(list = ls()); gc() ## load libs library(data.table) library(ggplot2) library(magrittr) ## set WD -------------------------------- # your dir here ... ## set vars ------------- currs <- c( 'usd', 'eur', 'chf', 'gbp' ) ############ ## RUN SIMULATION LOOP ------------------------------- simuls <- 1000L simul_dt <- data.table() for( s in seq_len(simuls) ) { #set.seed(111) usd <- runif(1) eur <- runif(1) chf <- runif(1) gbp <- runif(1) # snapshot of values at time t eurusd <- 1.12012 gbpusd <- 1.30890 eurchf <- 1.14135 eurgbp <- 0.85570 gbpchf <- 1.33373 usdchf <- 1.01896 ## symbolic task ------------ express <- expression( (eurusd - eur / usd) ^ 2 + (gbpusd - gbp / usd) ^ 2 + (eurchf - eur / chf) ^ 2 + (eurgbp - eur / gbp) ^ 2 + (gbpchf - gbp / chf) ^ 2 + (usdchf - usd / chf) ^ 2 ) ## define gradient and iterate to make descent to zero -------------- iter_max <- 1e+3 lr <- 1e-3 min_tolerance <- 0.00001 rm(grad_desc_func) grad_desc_func <- function( lr, curr_list ) { derivs <- character(length(curr_list)) deriv_vals <- numeric(length(curr_list)) grads <- numeric(length(curr_list)) # symbolic derivatives derivs <- sapply( curr_list, function(x){ D(express, x) } ) # derivative values deriv_vals <- sapply( derivs, function(x){ eval(x) } ) # gradient change values -deriv_vals * lr } ## get gradient values ---------- progress_list <- list() for( i in seq_len(iter_max) ) { grad_deltas <- grad_desc_func(lr, curr_list = currs) currency_vals <- sapply( currs , function(x) { # update currency values current_val <- get(x, envir = .GlobalEnv) new_delta <- grad_deltas[x] if(new_delta > -1 & new_delta < 1) { new_delta = new_delta } else { new_delta = sign(new_delta) } new_val <- current_val + new_delta if(new_val > 0 & new_val < 2) { new_val = new_val } else { new_val = current_val } names(new_val) <- NULL # change values of currencies by gradient descent step in global env assign(x, new_val , envir = .GlobalEnv) # save history of values for later plotting new_val } ) progress_list[[i]] <- c( currency_vals, eval(express) ) if( eval(express) < min_tolerance ) { break('solution was found') } } ## check results ---------- # print( # paste0( # 'Final error: ' # , round(eval(express), 5) # ) # ) # # print( # round(unlist(mget(currs)), 5) # ) progress_dt <- rbindlist( lapply( progress_list , function(x) { as.data.frame(t(x)) } ) ) colnames(progress_dt)[length(colnames(progress_dt))] <- 'error' progress_dt[, steps := 1:nrow(progress_dt)] progress_dt_melt <- melt( progress_dt , id.vars = 'steps' , measure.vars = colnames(progress_dt)[colnames(progress_dt) != 'steps'] ) progress_dt_melt[, simul := s] simul_dt <- rbind( simul_dt , progress_dt_melt ) } ggplot(data = simul_dt) + facet_wrap(~ variable, scales = 'free') + geom_line( aes( x = steps , y = value , group = simul , color = simul ) ) + scale_y_log10() + theme_minimal()


Kode untuk 1000 simulasi bekerja sekitar satu menit.

Kesimpulan


Inilah yang masih belum jelas bagi saya:

  • Apakah mungkin untuk menstabilkan solusi dengan cara matematika yang rumit;
  • apakah akan ada konvergensi dengan lebih banyak mata uang dan pasangan mata uang;
  • jika tidak ada stabilitas, maka untuk setiap snapshot data baru, mata uang kami akan berjalan sesuka mereka, jika Anda tidak memperbaiki seed PRNG, dan ini adalah kegagalan.

Seluruh gagasan itu tampak sangat kabur dengan tidak adanya prasyarat dan batasan yang dapat dipahami. Tapi itu menarik!

Yah, saya juga ingin mengatakan bahwa Anda dapat melakukannya tanpa OLS ketika datanya rumit, matriksnya tunggal, baik, atau ketika teorinya kurang dikenal (ehh ...).

Terima kasih eavprog untuk pesan awal.

Sampai jumpa!

Source: https://habr.com/ru/post/id450874/

More articles:


All Articles