Kata Pengantar

Selain artikel terakhir saya , saya juga ingin berbicara tentang topik MU ( M ulti U ser) MIMO. Saya telah menyebutkan satu artikel Profesor Haardt yang sangat terkenal di mana, bersama dengan rekan-rekannya, ia mengusulkan algoritma untuk memisahkan pengguna dalam Down Link berdasarkan metode linear, yaitu, Blok Diagonisasi saluran. Artikel ini memiliki jumlah kutipan yang mengesankan, dan juga merupakan pilar penerbitan untuk salah satu tugas ujian. Karena itu, mengapa tidak melihat dasar-dasar algoritma yang diusulkan?

Pernyataan masalah

Pertama, mari kita putuskan di area mana dalam tema MIMO kita akan bekerja sekarang.
Secara konvensional, semua metode transfer dalam kerangka teknologi MIMO dapat dibagi menjadi dua kelompok utama:

• Keragaman spasial

Tujuan utamanya adalah untuk meningkatkan kekebalan kebisingan transmisi. Saluran spasial, jika disederhanakan, saling menduplikasi, karena itu kami mendapatkan kualitas transmisi terbaik.

Contoh:
- Kode blok (misalnya, skema Alamuti );
- Kode berdasarkan pada algoritma Viterbi.

• Multiplexing spasial

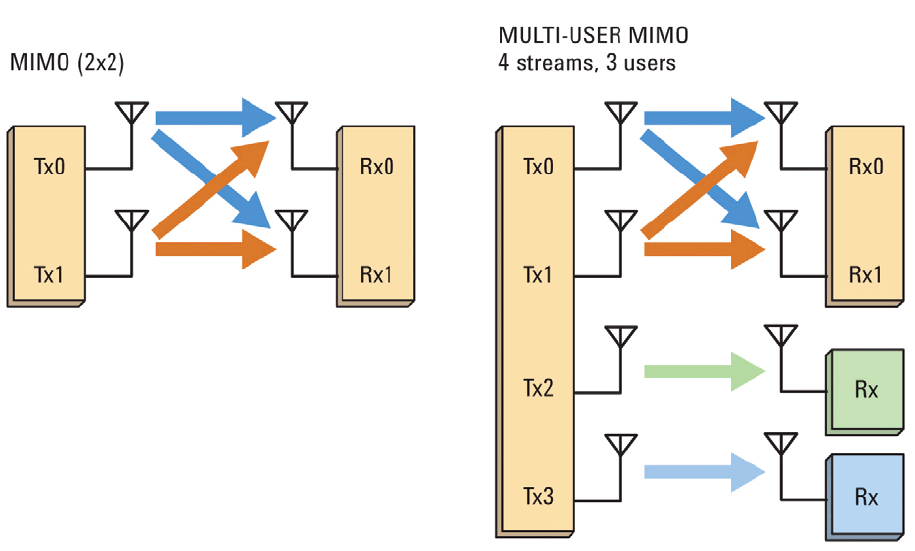
Tujuan utamanya adalah untuk meningkatkan kecepatan transmisi. Kami sudah membahas dalam artikel sebelumnya bahwa dalam kondisi tertentu saluran MIMO dapat dianggap sebagai serangkaian saluran SISO paralel. Sebenarnya, ini adalah ide sentral dari multiplexing spasial: untuk mencapai jumlah maksimum arus informasi independen. Masalah utama dalam hal ini adalah penindasan interferensi antar-saluran (inter-channel interferensi) , di mana ada beberapa kelas solusi:

- pemisahan saluran horizontal;
- vertikal (misalnya, algoritma V-BLAST);
- diagonal (misalnya, algoritma D-BLAST).

Tapi ini, tentu saja, tidak semuanya.

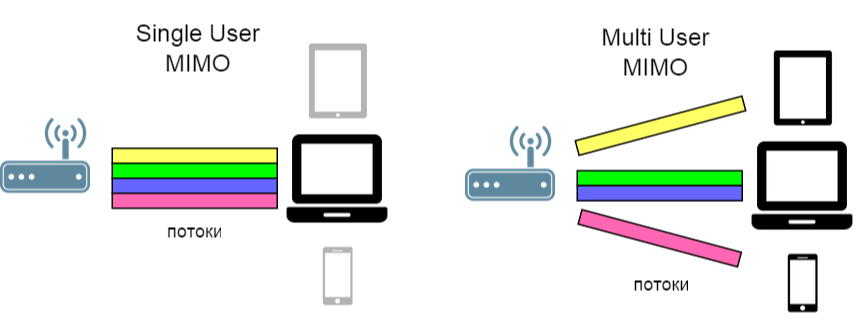
Gagasan multiplexing spasial dapat diperluas: untuk membagi tidak hanya saluran, tetapi juga pengguna (SDMA - Space Division Multiple Access).

( tautan ke sumber ilustrasi )

Akibatnya, dalam hal ini, sudah perlu untuk melawan gangguan antar pengguna . Untuk ini, sebuah algoritma yang disebut Block diagonalization Zero-Forcing diusulkan , yang kami pertimbangkan hari ini.

Deskripsi matematis

Mari kita mulai, seperti sebelumnya, dengan model sinyal yang diterima. Lebih tepatnya, kami menunjukkan pada diagram dari mana dan dari mana:

Matriks saluran dalam kasus ini memiliki bentuk:

dengan jumlah total antena pemancar , dan jumlah total antena penerima .

Penting :
Algoritma ini hanya dapat diterapkan asalkan jumlah antena pemancar lebih besar dari atau sama dengan jumlah total antena penerima:

Kondisi ini secara langsung mempengaruhi sifat diagonalisasi.

Jadi, model simbol yang diterima (sinyal) dapat ditulis dalam bentuk vektor sebagai:

Namun, lebih menarik untuk melihat rumus untuk pengguna tertentu:

Sebenarnya:

• Merupakan sinyal yang berguna untuk pengguna k-th,

  
  

• - ini adalah gangguan dari pengguna lain,

  
  

• - Kebisingan tambahan.

Jadi kita sampai pada rumusan tugas utama:

Anda dapat menemukan matriks seperti itu sehingga bagian interferensi menjadi nol!

Ini yang akan kita lakukan.

Deskripsi algoritma

Kami akan melakukan deskripsi dengan contoh, dan sebagai ilustrasi saya akan memberikan tangkapan layar tangan pertama , mengomentari sedikit tentang mereka.

Pertimbangkan pengguna pertama:

Mari kita bicara tentang langkah-langkah utama:

• Kami membuat beberapa matriks dari matriks saluran semua pengguna lain.

• Kami menguraikannya menggunakan metode SVD .

  
  

• Dalam matriks kami menemukan subruang noise (null-subruang) - matriks (mis., segala sesuatu yang melampaui pangkat matriks) - menunjukkannya )

  
  

• Kami menyusun dari matriks kebisingan ini dan konjugasi Hermitiannya beberapa matriks proyeksi .

  
  

Silakan:

• Sekarang bagian asli dari saluran matriks berkembang biak dengan matriks proyeksi yang dihasilkan .

  
  

• Kami menguraikan hasilnya melalui SVD.

  
  

• Dalam matriks pilih garis di mana - peringkat .

  
  

• Ubah posisi mereka dan dapatkan matriksnya (atau - di mana seperti yang ditunjukkan).

  
  

Maka prosedur ini akan diulang untuk setiap pengguna. Bukankah ini keajaiban matematika: menggunakan metode aljabar linier, kami menyelesaikan masalah teknis sepenuhnya!

Perhatikan bahwa dalam praktiknya tidak hanya matriks pra-pengkodean yang diperoleh digunakan, tetapi juga matriks pasca-pemrosesan dan matriks nilai singular (lihat slide ). Yang terakhir, misalnya, untuk menyeimbangkan daya sesuai dengan algoritma penuangan air yang sudah dikenal.

Kami memodelkan algoritma

Saya pikir itu tidak akan berlebihan untuk melakukan simulasi kecil untuk mengkonsolidasikan hasilnya. Untuk melakukan ini, kita akan menggunakan Python 3, yaitu:

import numpy as np 

untuk perhitungan dasar, dan:

 import pandas as pd 

untuk menampilkan hasilnya.

 class ZeroForcingBD: def __init__(self, H, Mrs_arr): Mr, Mt = np.shape(H) self.Mr = Mr self.Mt = Mt self.H = H self.Mrs_arr = Mrs_arr def __routines(self, H, mr, shift): # used in self.process() - See example above for illustration # inputs: # H - the whole channel matrix # mr - number of receive antennas of the i-th user # shift - how much receive antennas were considered before # outputs: # Uidx, Sigmaidx, Vhidx - SVD decomposition of the H_iP_i # d - rank of the hat H_i # Hidx - H_i (channel matrix for the i-th user) # r - rank of the H_i Hidx = H[0+shift:mr+shift,:] # H_i (channel matrix for the i-th user) r = np.linalg.matrix_rank(Hidx) # rank of the H_i del_idx = [i for i in range(0+shift, mr+shift, 1)] # row indeces of H_i in H H_hat_idx = np.delete(H, del_idx, 0) # hat H_i d = np.linalg.matrix_rank(H_hat_idx) # rank of the hat H_i U, Sigma, Vh = np.linalg.svd(H_hat_idx) # SVD Vhn = Vh[d:, :] # null-subspace of V^H Vn = np.matrix(Vhn).H # null-subspace of V Pidx = np.dot(Vn, np.matrix(Vn).H) # projection matrix Uidx, Sigmaidx, Vhidx = np.linalg.svd(np.dot(Hidx, Pidx)) # SVD of H_iP_i return Uidx, Sigmaidx, Vhidx, d, Hidx, r def process(self): # used in self.obtain_matrices() # outputs: # F - whole filtering (pre-coding) matrix (array of arrays) # D - whole demodulator (post-processing) matrix (array of arrays) # H - the whole channel matrix (array of arrays) shift = 0 H = self.H F = [] D = [] Hs = [] for mr in self.Mrs_arr: Uidx, Sigmaidx, Vhidx, d, Hidx, r = self.__routines(H, mr, shift) Vhidx1 = Vhidx[:r,:] # signal subspace Fidx = np.matrix(Vhidx1).H F.append(Fidx) D.append(Uidx) Hs.append(Hidx) shift = shift + mr return F, D, Hs def obtain_matrices(self): # used to obtain pre-coding and post-processing matrices # outputs: # FF - whole filtering (pre-coding) matrix # DD - whole demodulator (post-processing) matrix (array of arrays) F, D, Hs = self.process() FF = np.hstack(F) # Home Task: calculation of the demodulator matrices :) return FF 

Misalkan kita memiliki 8 antena pengirim dan 3 pengguna yang memiliki 3, 2 dan 3 antena penerima, masing-masing:

 Mrs_arr = [3,2,3] # 1st user have 3 receive antennas, 2nd user - 2 receive antennas, 3d user - 3 receive antennas Mr = sum(Mrs_arr) # total number of the receive antennas Mt = 8 # total number of the transmitt antennas H = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2); #Rayleigh flat faded channel matrix (MrxMt) 

Kami menginisialisasi kelas kami dan menerapkan metode yang sesuai:

 BD = ZeroForcingBD(H, Mrs_arr) F, D, Hs = BD.process() FF = BD.obtain_matrices() 

Kami membawa ke formulir yang dapat dibaca:

 df = pd.DataFrame(np.dot(H, FF)) df[abs(df).lt(1e-14)] = 0 

Dan mari kita angkat sedikit kejelasan (meskipun Anda bisa tanpanya):

 print(pd.DataFrame(np.round(np.real(df),100))) 

Anda harus mendapatkan sesuatu seperti ini:

Sebenarnya, ini dia blok, ini dia dan diagonalisasi. Dan meminimalkan gangguan.

Hal-hal seperti itu.

Sastra

1. Spencer, Quentin H., A. Lee Swindlehurst, dan Martin Haardt. "Metode zero-forcing untuk multiplexing downlink spasial di saluran MIMO multiuser." Transaksi IEEE pada pemrosesan sinyal 52.2 (2004): 461-471.
2. Martin Haard " Pemrosesan Robust Transmit untuk Sistem MIMO Multi-Pengguna "

PS

Kepada staf pengajar dan persaudaraan mahasiswa dari profesi asli saya, saya menyapa!