Selama bertahun-tahun saya telah memberikan kursus dalam kombinatorik dan grafik untuk siswa matematika dan ilmuwan komputer (bagaimana di Rusia, ilmuwan komputer?), Sebelumnya di Universitas Akademik, dan sekarang di
Universitas Negeri St. Petersburg . Program kami dirancang sedemikian rupa sehingga topik-topik ini diadakan sebagai bagian dari "ilmu komputer teoretis" (topik lain di dalamnya adalah algoritme, kompleksitas, bahasa, dan tata bahasa). Saya tidak bisa mengatakan bagaimana secara metafisik atau historis dibenarkan: meskipun demikian, objek kombinatorial (grafik, sistem set, permutasi, kotak-kotak angka, dll) mulai dipelajari jauh sebelum munculnya komputer, dan sekarang yang terakhir, meskipun penting, masih jauh dari satu-satunya alasan untuk minat dia. Tetapi melihat spesialis yang sangat dalam kombinatorik dan ilmu komputer teoritis secara mengejutkan sering orang yang sama: Lovas, Alon, Semeredi, Razborov dan seterusnya. Mungkin ada alasan untuk ini. Dalam pelajaran saya, juara pemrograman olimpiade sering menawarkan solusi yang sangat sepele untuk masalah yang kompleks (saya tidak akan menuliskannya, siapa pun yang ingin melihat kekuatan kode teratas). Secara umum, saya berpikir bahwa beberapa hal dari kombinatorik mungkin menarik bagi masyarakat. Bicaralah jika ada yang salah atau tidak.
Biarkan Anda perlu membangun permutasi angka acak dari 1 hingga
$ inline $ n $ inline $ sehingga semua permutasi sama kemungkinannya. Ini dapat dilakukan dengan banyak cara: misalnya, pertama pilih secara acak elemen pertama, kemudian dari sisa kedua dan seterusnya. Atau Anda dapat melakukan sebaliknya: pilih titik secara acak
$ sebaris $ t_1, t_2, \ ldots, t_n $ sebaris $ di segmen tersebut
$ inline $ [0,1] $ inline $ , dan lihat bagaimana mereka dipesan. Mengganti yang terkecil dari angka dengan 1, yang kedua dengan 2, dan seterusnya, kita mendapatkan permutasi acak. Mudah dilihat semuanya
$ inline $ n! $ inline $ permutasi juga memungkinkan. Anda tidak perlu untuk meregangkan
$ inline $ 0,1 $ inline $ pilih poin, dan, misalnya, di antara angka dari 1 hingga
$ inline $ n $ inline $ . Kebetulan dimungkinkan di sini (untuk suatu segmen, mereka juga mungkin, tetapi dengan probabilitas nol, sehingga mereka tidak mengganggu kami) - Anda dapat menanganinya dengan cara yang berbeda, misalnya, menata ulang angka-angka kebetulan. Atau ambil
N yang lebih besar sehingga kemungkinan kebetulannya kecil (seperti saat)
$ inline $ N = 365 $ inline $ , dan
$ inline $ n $ inline $ ada jumlah siswa di kelas Anda, dan kami berbicara tentang kebetulan dua hari ulang tahun.) Variasi pada metode ini: secara acak
$ inline $ n $ inline $ poin dalam satuan persegi dan melihat bagaimana ordinat mereka dipesan relatif terhadap abscissas. Variasi lain: tandai di segmen
$ inline $ n-1 $ inline $ tunjuk dan lihat bagaimana panjang segmen yang dibagi dibagi. Poin utama dalam pendekatan ini adalah independensi pengujian, sesuai dengan hasil penyusunan ulang acak. Andrei Nikolaevich Kolmogorov mengatakan bahwa teori probabilitas adalah teori ukuran plus kemandirian - dan ini akan dikonfirmasi oleh siapa saja yang telah berurusan dengan probabilitas.
Saya akan menunjukkan bagaimana ini membantu, menggunakan contoh
rumus kait untuk pohon :
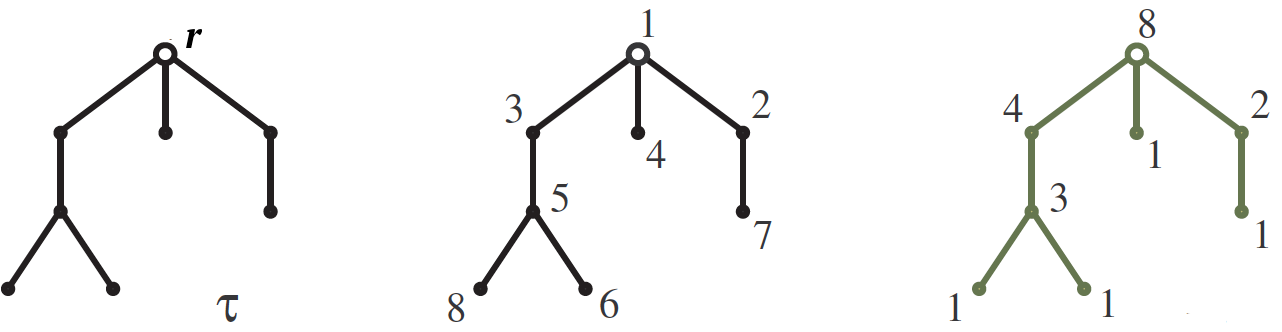
Biarkan
$ inline $ \ tau $ inline $ - ditangguhkan oleh root
$ inline $ r $ inline $ pohon dengan
$ inline $ n $ inline $ puncak tumbuh seperti pada gambar. Tujuan kami adalah menghitung jumlahnya
$ inline $ S (\ tau) $ inline $
penomoran puncak pohon
$ inline $ \ tau $ inline $ angka dari 1 hingga
$ inline $ n $ inline $ sedemikian rupa sehingga untuk setiap sisi angka di bagian atas lebih besar daripada di bagian bawah. Salah satu dari angka-angka ini ditunjukkan di gambar tengah. Jawabannya dirumuskan menggunakan
ukuran kait . Kait
$ inline $ H (v) $ inline $ puncak
$ inline $ v $ inline $ sebut saja subtree yang tumbuh dari simpul ini, dan ukurannya hanyalah jumlah simpul di dalamnya. Panjang kait ditulis dalam gambar kanan di sebelah simpul yang sesuai. Jadi, jumlah angkanya adalah
$ inline $ n! $ inline $ dibagi dengan produk ukuran kait, jadi untuk contoh kita
$$ menampilkan $$ S (\ tau) = \, \ frac {8!} {8 \ cdot 4 \ cdot 3 \ cdot 2 \ cdot 1 \ cdot 1 \ cdot 1 \ cdot 1} = 210. $$ display $ $
Kita dapat membuktikan formula itu dengan cara yang berbeda, misalnya dengan menginduksi jumlah simpul, tetapi pandangan kita tentang permutasi acak memungkinkan kita untuk melakukan pembuktian tanpa perhitungan. Lebih baik tidak hanya karena keanggunan, tetapi juga karena ia menggeneralisasi dengan baik untuk pertanyaan yang lebih halus tentang penomoran dengan ketidaksetaraan yang ditentukan, tetapi bukan tentang hal itu sekarang. Jadi, ambil
n bilangan real yang berbeda dan letakkan secara acak di atas pohon, masing-masing dengan satu angka, semuanya
$ inline $ n! $ inline $ permutasi juga memungkinkan. Berapa kemungkinan bahwa untuk setiap sisi, jumlah di puncak sudut lebih besar daripada jumlah di puncaknya? Jawabannya adalah:
$ inline $ S (\ tau) / n! $ inline $ , dan itu tidak tergantung pada satu set angka. Dan jika itu tidak tergantung, maka mari kita pertimbangkan angka-angka yang juga dipilih secara acak - untuk kepastian, dalam interval
$ inline $ [0,1] $ inline $ . Alih-alih memilih angka secara acak pada awalnya dan kemudian menempatkannya secara acak di bagian atas pohon, kita dapat memilih angka secara acak dan mandiri di setiap simpul: pengaturan ulang mereka akan acak secara otomatis. Dengan cara ini
$ inline $ S (\ tau) / n! $ inline $ ini adalah probabilitas untuk nomor independen acak
$ inline $ \ xi (v) $ inline $ yang dipilih untuk setiap titik
$ inline $ v $ inline $ kayu
$ inline $ \ tau $ inline $ , semua ketidaksetaraan formulir
$ inline $ \ xi (v)> \ xi (u) $ inline $ untuk semua ujungnya
$ inline $ v \ to u $ inline $ ,
$ inline $ v $ inline $ Apakah simpul atas tulang rusuk, dan
$ inline $ u $ inline $ - bawah. Kami merumuskan kondisi ini dalam bentuk yang setara, tetapi dengan cara yang sedikit berbeda: untuk setiap titik
$ inline $ v $ inline $ peristiwa semacam itu harus terjadi - saya akan menunjuknya
$ inline $ Q (v) $ inline $ : angka
$ inline $ \ xi (v) $ inline $ - maksimum di antara semua angka di simpul subtree hook
$ inline $ H (v) $ inline $ .
Catat itu
$ inline $ \ frac {1} {| H (v) |} $ inline $ ini adalah probabilitas suatu peristiwa
$ inline $ Q (v) $ inline $ . Bahkan, di kait
$ inline $ H (v) $ inline $ tersedia
$ inline $ | H (v) | $ inline $ simpul dan jumlah kait maksimum dipetakan ke masing-masing dengan probabilitas yang sama
$ inline $ \ frac {1} {| H (v) |} $ inline $ . Dengan demikian, kait rumus
$ inline $ S (\ tau) / n! = \ prod_v \ frac {1} {| H (v) |} $ inline $ dapat dirumuskan sebagai berikut: probabilitas bahwa semua peristiwa terjadi sekaligus
$ inline $ Q (v) $ inline $ sama dengan produk dari probabilitas peristiwa ini. Alasan untuk ini mungkin banyak berbeda, tetapi yang pertama muncul di pikiran bekerja di sini: peristiwa ini independen. Untuk memahami ini, mari kita lihat, misalnya, di sebuah acara
$ inline $ Q (r) $ inline $ (sesuai dengan root). Terdiri dari fakta bahwa angka di root lebih besar dari semua angka lain dalam simpul, dan peristiwa lain berhubungan dengan perbandingan di antara mereka sendiri dari angka yang ditulis bukan di root. Yaitu
$ inline $ Q (r) $ inline $ tentang nomor tersebut
$ inline $ \ xi (r) $ inline $ dan
himpunan angka pada simpul lain, dan semua peristiwa lainnya adalah
urutan angka pada simpul selain dari root. Seperti yang telah kita bahas, "ketertiban" dan "banyak" adalah independen, oleh karena itu acara
$ inline $ Q (r) $ inline $ independen dari orang lain. Turun ke pohon, kita mendapatkan bahwa semua peristiwa ini independen, dari mana yang diperlukan berikut.
Biasanya, rumus untuk kait adalah rumus untuk penomoran bukan simpul di pohon, tetapi sel-sel dalam
diagram Young 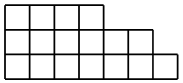
meningkat ke arah sumbu koordinat, dan kait ada lebih mirip kait daripada untuk pohon. Tetapi formula ini terbukti lebih rumit dan layak mendapat pos terpisah.
Karena saya punya omong-omong, saya tidak bisa membantu tetapi berbicara tentang model
diagram Young acak . Diagram muda adalah sosok seperti itu
$ inline $ n $ inline $ kuadrat unit, panjang barisnya meningkat dari bawah ke atas, dan panjang kolom dari kiri ke kanan. Jumlah Bagan Area Young
$ inline $ n $ inline $ ditunjukkan
$ inline $ p (n) $ inline $ ,
fungsi penting ini berperilaku dengan cara yang menarik dan tidak biasa: misalnya, ia tumbuh lebih cepat daripada polinomial apa pun, tetapi lebih lambat dari eksponen mana pun. Oleh karena itu, khususnya, menghasilkan diagram Young acak (jika kita ingin semua diagram area
$ inline $ n $ inline $ kemungkinan besar sama
$ inline $ 1 / p (n) $ inline $ ) bukan masalah sepele. Misalnya, jika Anda menambahkan sel satu per satu, memilih tempat untuk menambahkan secara acak, bagan yang berbeda akan memiliki probabilitas yang berbeda (jadi, probabilitas bagan garis tunggal ternyata adalah
$ inline $ 1/2 ^ {n-1} $ inline $ .) Ternyata ukuran menghibur pada diagram, tetapi tidak seragam. Seragam dapat diperoleh sebagai berikut. Ambil nomornya
$ inline $ t \ in (0,1) $ inline $ , untuk tujuan kami, angka-angka di daerah paling cocok
$ inline $ 1- \ mathrm {const} / \ sqrt {n} $ inline $ . Untuk masing-masing
$ inline $ k = 1,2, \ ldots $ inline $
pertimbangkan distribusi geometrik pada bilangan bulat non-negatif dengan mean
$ inline $ t ^ k $ inline $ (mis. probabilitas nomor tersebut
$ inline $ m = 0,1, \ ldots $ inline $ sama dengan
$ sebaris $ t ^ {km} (1-t ^ k) $ sebaris $ ) Kami memilih untuk itu variabel acak
$ inline $ m_k $ inline $ (ada banyak cara untuk mengatur ini). Pada umumnya
$ inline $ k $ inline $ kemungkinan besar 0. Mari kita lihat diagram Young di mana
$ inline $ m_k $ inline $ baris panjang
$ inline $ k $ inline $ di setiap
$ inline $ k = 1,2, \ ldots $ inline $ . Saya menyebutnya
metode kapal karena luas total
terkadang sama dengan
$ inline $ n $ inline $ . Jika tidak sama, maka ulangi percobaan. Sebenarnya setara
$ inline $ n $ inline $ cukup sering, jika cerdas memilih
$ inline $ t \ in (0,1) $ inline $ . Saya mengundang pembaca untuk membuktikan secara independen bahwa semua diagram pada area tertentu sama-sama memungkinkan dan memperkirakan jumlah langkah.