29 Maret 2019 - Michael Trott, Peneliti Utama
Entri
Dalam apa yang disebut "SI baru" -
versi terbaru dari Sistem Satuan Internasional , yang akan menentukan tujuh unit dasar pengukuran (kedua, meter, kilogram, ampere, kelvin, mol dan candela) dan yang akan mulai berlaku pada 20 Mei 2019, semua unit SI akan menjadi ditentukan melalui nilai-nilai tepat dari konstanta fisik dasar. Akibatnya, semua unit SI di atas (Newton, Volt, Ohm, Pascal, dll.) Pada akhirnya akan dinyatakan dalam konstanta fundamental. (Akhirnya, fisika fundamental secara harfiah akan mengendalikan kehidupan kita sehari-hari βΊ)
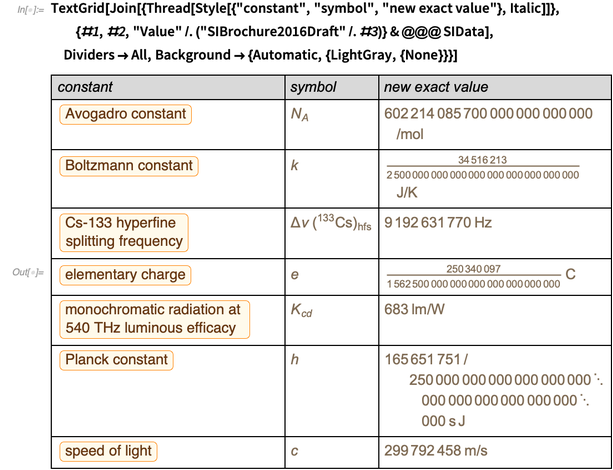
Tabel di bawah ini menunjukkan bagaimana semuanya akan berubah dari Senin malam 20 Mei hingga Selasa pagi 21 Mei tahun ini.
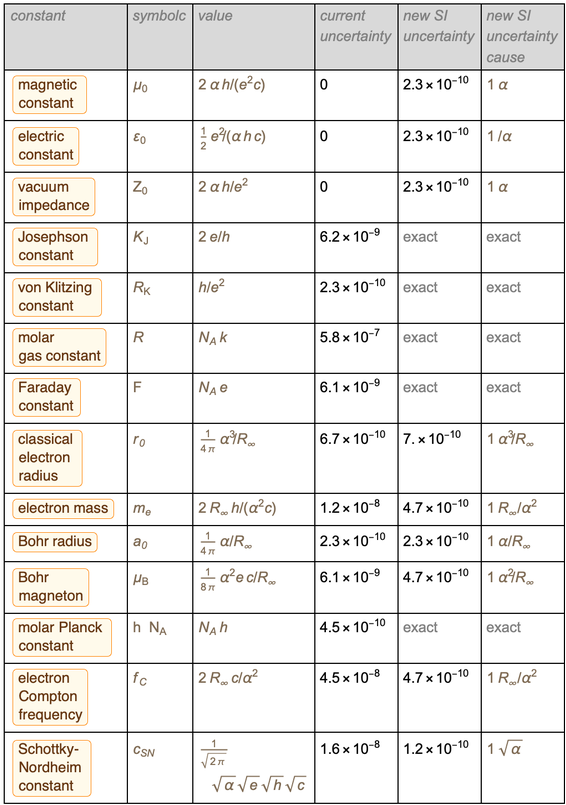
Komputasi data dari tabel ini adalah tujuan blog ini. Jadi, mari kita mulai dengan ikhtisar singkat tentang apa yang akan berubah dalam SI baru.
Selain nilai tepat yang diketahui dari kecepatan cahaya, dalam empat minggu empat konstanta fisik lainnya - konstanta Planck, konstanta Boltzmann, konstanta Avogadro dan konstanta Millikan (sering disebut muatan listrik elementer) - akan memiliki nilai yang tepat. Keputusan tentang perubahan ini dibuat secara internasional pada bulan November tahun lalu (saya menulis tentang itu di terakhir saya
blog).
Di bawah ini adalah potongan halaman 12 dari draft
SI brosur saat ini .
Perhatikan bahwa dalam definisi ini, angka desimal dimaksudkan sebagai angka desimal yang tepat, bukan, katakanlah, nomor mesin pada komputer yang memiliki presisi hingga dan bukan angka yang tepat. Frekuensi transisi dalam struktur prima split Cs-133, kecepatan cahaya dan "efisiensi cahaya" sudah memiliki nilai yang tepat hari ini.
Dunia membahas perubahan di masa depan
Perubahan ini akan memiliki beberapa konsekuensi menarik untuk konstanta fisik lainnya: beberapa konstanta yang saat ini diukur dan memiliki kesalahan akan menjadi akurat, dan beberapa konstanta yang saat ini akurat akan memiliki nilai perkiraan dengan kesalahan terbatas di masa mendatang. . Perubahan ini tidak dapat dihindari untuk menjamin konsistensi sistem secara keseluruhan.
Edisi pertama
Fisika Dunia tahun ini membahas masalah ini dalam
sepucuk surat kepada editor dari William Hough; dia menulis:
Dengan fiksasi muatan pada elektron ( e ) dan konstanta Planck ( h ), semua unit fisik sekarang "diabadikan dalam batu", yang sangat bagus. Tapi itu menimbulkan satu pertanyaan aneh. Struktur halus konstan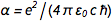 
di mana c adalah kecepatan cahaya dan 
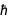itu 
. Dari persamaan yang dikenal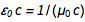 
dan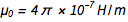 
kami dengan cepat menemukan itu 
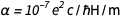. Ini, tentu saja, adalah angka murni dengan kuantitas tanpa dimensi, dan sekarang ditetapkan selamanya sama dengan 1 / 137.13601, yang sangat dekat dengan nilai yang diterima. Ini tidak mengherankan, karena nilai yang terakhir akan digunakan dalam nilai-nilai baru yang disepakati untuk e dan β . Tetapi alam memiliki nilainya sendiri, tidak diketahui oleh kita saat ini, yang, karena ini, diabadikan dalam intan. Kita dapat dimaafkan karena mengisyaratkan bahwa kita tahu lebih baik daripada alam. Tetapi bagaimana jika teori masa depan tentang alam semesta diterima dan memberikan makna yang tepat 
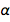Mana yang sangat berbeda dari nilai yang diterima? Bisakah ini terjadi? Telah ada upaya untuk menemukan nilai teoritis untuk Ξ± , tetapi mereka termasuk mengancam dan elektrodinamika kuantum yang kontroversial.
Masalahnya adalah bahwa dalam sistem SI baru keduanya
dan
sekarang akan memiliki nilai yang tidak akurat dengan beberapa kesalahan. Dalam blog ini, kita akan menggunakan Bahasa Wolfram dan pengetahuannya tentang unit fisik dan konstanta untuk melihat bagaimana konstanta fisik ini dan lainnya mendapatkan (atau kehilangan) kesalahan, dan mengapa ini merupakan konsekuensi matematis dari definisi unit dasar.
Tinjauan Singkat Bahan Bahasa Wolfram Terkait
Bahasa Wolfram adalah media unik untuk melakukan eksperimen numerik dan perhitungan simbolik, mengidentifikasi kemungkinan konsekuensi. Selain kemampuan komputasi umum, tiga komponen sistem sangat berguna di sini:
1) Wolfram Unit bahasa dan struktur jumlah fisik.
Unit klasik (seperti meter, kaki, dll.) Dapat digunakan dalam perhitungan dan visualisasi. Dan, tentu saja, dalam konversi satuan ukuran.
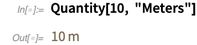
Konversi ke unit AS biasa menghasilkan sebagian kecil (daripada nilai perkiraan bilangan real!) Karena rasio yang jelas dari kedua unit.
Fisikawan (terutama) suka menggunakan satuan "alami". Seringkali unit alami ini hanyalah konstanta fisik atau kombinasinya. Misalnya, kecepatan cahaya (input bahasa alami digunakan di sini).
Dinyatakan dalam satuan SI (karena ini adalah kecepatan dan satuan dalam meter dan detik diperlukan), kecepatan cahaya memiliki nilai yang akurat.
Di sisi lain, konstanta Planck saat ini tidak memiliki nilai yang pasti. Dengan demikian, nilainya, dinyatakan dalam satuan dasar SI, adalah angka desimal perkiraan.
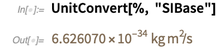
Harap dicatat bahwa keakuratan 6.626070 ... mencerminkan jumlah angka yang diketahui.
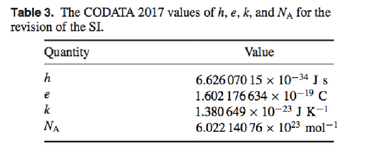
Ini adalah nilai yang direkomendasikan terakhir untuk konstanta Planck yang diterbitkan dalam
CODATA 2017 sebagai persiapan untuk penyempurnaan konstanta. Di bawah ini adalah tabel terkait:
Konstanta fisik (atau kombinasinya) yang menghubungkan dua kuantitas fisik sering dapat digunakan sebagai satuan alami. Contoh paling sederhana adalah pengukuran kecepatan dalam hal kecepatan cahaya atau torsi mikroskopis dalam hal
β . Atau energi dapat diukur dalam hal massa dengan faktor tersirat
. Fungsi
DimensionalCombinations dapat digunakan untuk mencari kombinasi konstanta fisik yang memungkinkan Anda untuk menghubungkan dua kuantitas fisik yang diberikan. Misalnya, hubungan berikut antara massa dan energi dapat dibangun:
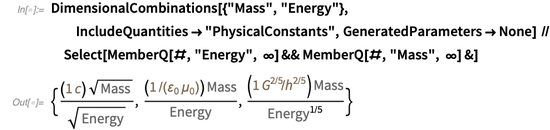
Kesetaraan pertama mencerminkan formula terkenal Einstein
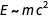
, yang kedua adalah setara dengan relasi pertama, dan yang ketiga - (secara dimensional) menyatakan itu
.
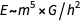
2) Kelas entitas "
PhysicalConstant " baru-baru ini ditambahkan ke
Wolfram Knowledgebase .
Fungsi dan objek dalam Bahasa Wolfram adalah "terlahir secara komputasi", yaitu, mereka siap digunakan dalam komputasi. Tetapi untuk menggambarkan dan mensimulasikan dunia nyata, Anda membutuhkan data tentang dunia nyata. Struktur entitas adalah cara yang mudah dan terintegrasi penuh untuk mendapatkan data tersebut. Di bawah ini adalah beberapa data tentang elektron, proton, dan neutron.
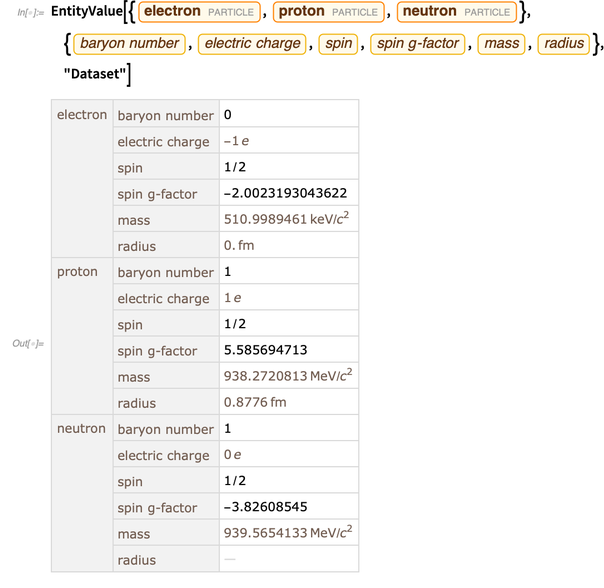
Salah satu unit entitas baru adalah konstanta fisik. Saat ini, Pangkalan Pengetahuan berisi lebih dari 250 konstanta fisik.
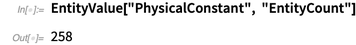
Di bawah ini adalah selusin contoh yang dipilih secara acak. Selain itu, tanpa definisi yang jelas tentang apa konstanta adalah konstanta fisik, massa partikel fundamental, parameter Lagrange dari model standar, dll. Untuk kenyamanan, daftar ini juga berisi
konstanta astronomi yang sesuai dengan Astronomical Almanac.
Sebagian besar konstanta fisik dasar disebut konstanta kelas C dalam
karya terkenal Jean-Marc Levy-Leblond. Berikut ini adalah konstanta kelas C dan B.
Ambil, misalnya, satuan waktu alami, waktu Planck. Fungsi
ToEntity dan
FromEntity membuatnya mudah untuk bolak-balik antara konstanta fisik sebagai unit dan konstanta fisik sebagai entitas. Entitas yang terkait dengan satuan waktu Planck ditunjukkan di bawah ini.
Basis pengetahuan memiliki banyak meta-informasi tentang dia, misalnya, nilainya dalam daftar CODATA terbaru.
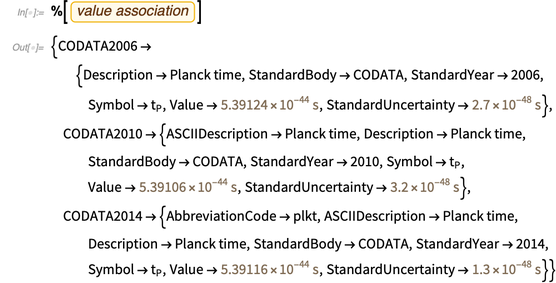
Kesimpulan terakhir, yang mengandung arti dan kesalahan, membawa kita ke fungsi penting ketiga, yang akan berguna kemudian:
3) Pengantar fungsi
Sekitar [] dalam versi 12 Bahasa Wolfram. Fungsi
Sekitar [] memberikan nilai yang tidak akurat, menunjukkan nilai rata-rata dan kesalahan. Model aritmatika
Around [] didasarkan pada
GUM (Panduan untuk Mengekspresikan Kesalahan Pengukuran) - jangan bingung dengan Leibniz Plus-Minus-calculus. Berikut ini adalah nilai dengan kesalahan.
Aspek yang paling penting dan berguna dari komputasi dengan nilai-nilai yang memiliki kesalahan adalah mereka memperhitungkan korelasi. Penggunaan naif dari nilai-nilai tersebut dalam angka atau interval aritmatika dapat meremehkan atau melebih-lebihkan kesalahan yang dihasilkan.
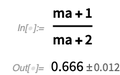
Di bawah ini kita melihat bahwa fungsi
AroundReplace [] memperhitungkan korelasi akun.
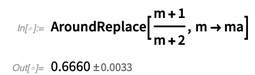
Kembali ke surat kepada editor
Sekarang mari kita gunakan ketiga komponen ini dan surat William Hough yang lebih rinci kepada editor.
Pada nilai perkiraan saat ini untuk
e dan
β , kedua nilai untuk konstanta struktur halus ini konsisten dalam batas kesalahannya. Yang pertama adalah ekspresi dari huruf ke editor, dan yang kedua adalah kuantitas (
Kuantitas []), yang mewakili konstanta struktur halus.
Setiap beberapa tahun, CODATA menerbitkan nilai resmi konstanta fundamental (lihat
konstanta struktur halus ); seperti yang saya katakan, nilai yang digunakan dalam Bahasa Wolfram adalah nilai CODATA terbaru dan kesalahan terakhir tercermin dalam keakuratan angka tersebut.
Harap dicatat bahwa konstanta struktur halus yang diukur secara langsung sedikit lebih akurat daripada konstanta yang menyatakan konstanta struktur halus melalui konstanta lain.
Jika kita menggunakan nilai tepat yang akan datang dari
e dan
β ,
dan menggunakan nilai tepat saat ini
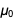
, kami mendapatkan nilai tepat berikut untuk konstanta struktur halus dalam bentuk
.
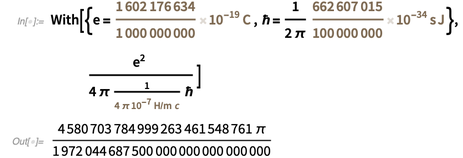
Tidak mungkin Tuhan, yang bahkan tidak
bermain dadu , akan memilih angka seperti itu untuk nilainya
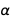
di alam semesta kita. Ini berarti bahwa sementara
e dan
β ditetapkan dalam SI baru, nilai pastinya saat ini
dan
mau tidak mau harus "dipisahkan" (lihat juga
artikel Goldfarb pada kuantitas
SI baru). (Kami akan kembali ke alasannya
dan
segera menjadi tidak akurat.)
Ini berarti bahwa setelah 20 Mei tahun ini, hasil ini akan berbeda dari yang diberikan di bawah ini.
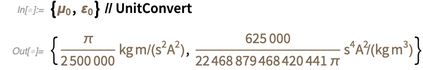
(Dalam catatan singkat, kelas entitas "
PhysicalConstant " juga memiliki nilai estimasi untuk konstanta, seperti konstanta struktur halus):
Sekarang, terlepas dari argumen teologis tentang bentuk pasti dari struktur halus yang konstan, dari sudut pandang fisik, mengapa
dan
harus tidak akurat? Sebagai argumen probabilitas, mari pertimbangkan
. Salah satu hasil yang paling menonjol adalah hukum Coulomb.
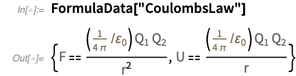
Dalam sistem SI yang
ada , ampere memiliki definisi "tepat":
Sebuah ampere adalah arus searah, yang, jika didukung dalam dua konduktor paralel dengan panjang tak terbatas dengan penampang bundar sedikit dan ditempatkan pada jarak 1 meter dalam ruang hampa, akan menciptakan gaya antara konduktor ini sama dengan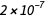 
Newton per meter panjang. Definisi ini menggunakan besaran mekanis murni Newton dan meter (yaitu, setelah ekspansi, ini adalah detik, meter dan kilogram). Tidak ada hubungan yang dibuat dengan muatan elektron, dan dalam sistem SI yang ada, muatan dasar adalah kuantitas yang diukur secara eksperimental.
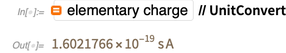
Dan nilai yang diukur secara eksperimental ini telah berubah selama bertahun-tahun, menjadi lebih akurat.
Gaya di sisi kiri hukum Coulomb (dinyatakan dalam Newton) berisi satuan dasar kilogram, yang, setelah nilai konstanta Planck menjadi konstan, juga menjadi dapat didefinisikan dengan tepat. Karena tidak ada alasan untuk percaya bahwa semua hukum alam dapat dinyatakan dalam bilangan rasional yang terbatas, satu-satunya "bagian yang bergerak" dalam hukum Coulomb adalah
. Nilai numeriknya harus ditentukan, dan itu akan membuat sisi kiri dan kanan hukum Coulomb bertepatan.
Dari sudut pandang fisika yang lebih mendasar, konstanta struktur halus adalah konstanta interaksi, yang menentukan kekuatan interaksi elektromagnetik. Dan, mungkin suatu hari, fisika dapat menghitung nilai konstanta struktur halus, tetapi kita masih jauh dari ini. Hanya memilih definisi unit tidak dapat memperbaiki nilainya
.
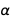
Keduanya benar-benar
dan
menjadi tidak tetap, atau apakah mungkin untuk membuat salah satu dari mereka akurat? Karena kecepatan cahaya dan rasionya sudah akurat
jika salah
atau
akurat, yang lain juga harus akurat. Kita tahu bahwa paling tidak seseorang harus menjadi tidak berkomitmen, sehingga keduanya harus tidak berkomitmen.
Nilai-nilai yang sekarang diberikan oleh konstanta Planck, konstanta Boltzmann, konstanta Avogadro, dan muatan elementer tidak ditentukan secara arbitrer atau pun tidak sepenuhnya ditentukan. Mereka ditentukan hingga sekitar delapan karakter, sehingga unit pengukuran yang mereka tentukan setelah 20 Mei sesuai dengan "ukuran" unit yang mereka tentukan sebelum 20 Mei. Tetapi angka-angka di kanan bawah tidak ditentukan. Dengan demikian, nilai nilai tepat masa depan dari muatan dasar dapat
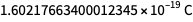
tapi tidak
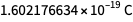
. Adalah pisau cukur dan rasionalitas Occam yang memungkinkan kita untuk menggunakannya
.
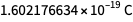
Pada tingkat yang lebih teknis, substitusi dalam perhitungan sebelumnya adalah melalui term
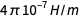
dalam formula
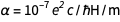amp digunakan sebelum redefinisi (ingat
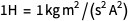
), tetapi nilai yang tepat dari muatan dasar juga digunakan, yang berarti definisi ampere setelah redefinisi. Dan kita harus selalu berada dalam satu sistem unit.
Penghitungan tabel formulir yang dioptimalkan kesalahan
Jadi, muncul pertanyaan alami: apa arti makna "tidak tetap" ini? Di blog terakhir saya, saya secara manual membuat nilai baru
. Apa yang dapat dilakukan secara manual dapat dilakukan dengan menggunakan program komputer, jadi mari kita laksanakan program kecil yang menghitung bentuk turunan dari konstanta fisik yang dioptimalkan kesalahan. Dalam pendekatan berorientasi masa depan, kelas entitas tujuh konstanta yang mendefinisikan SI baru sudah tersedia.
Di bawah ini adalah konstanta yang akan memiliki nilai tepat di SI baru.
Nilai saat ini dari konstanta ini bersama-sama dengan kesalahannya (dihitung menggunakan fungsi
Sekitar []) memiliki bentuk:
Menggunakan kelas entitas "
PhysicalConstant " kita bisa mendapatkan nilai kuantitas fisik baru yang akan datang. Perhatikan bahwa, seperti dalam semua bahasa komputer, bilangan bulat dan bilangan rasional yang tepat adalah bilangan bulat eksplisit atau bilangan rasional (tetapi bukan desimal).
Banyak konstanta fisik dapat dihubungkan dengan persamaan yang diberikan oleh teori-teori fisika dari berbagai bidang fisika. Di masa depan, kami ingin membatasi diri pada teori fenomena elektromagnetik fundamental, di mana kesalahan konstanta akan dikurangi menjadi kesalahan konstanta struktur halus
dan Rydberg konstan
. Jika kita memasukkan, misalnya, fenomena gravitasi, kita harus menggunakan konstanta gravitasi G, yang diukur secara independen, meskipun ia memiliki kesalahan yang sangat besar (itulah sebabnya NSF memiliki apa yang disebut "
Tantangan Big-G ").
Selanjutnya, kami membatasi diri untuk jumlah listrik, magnetik, dan massa, yang kesalahannya dikurangi menjadi satuan
dan
.
Di bawah ini kami menggunakan fungsi
Sekitar baru untuk mengekspresikan nilai dengan kesalahan yang sesuai
dan
.
Saat ini, menurut CODATA 2014, kesalahan relatif untuk
sekitar
, dan untuk
tentang
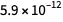
. Seperti yang Anda lihat, kesalahan untuk
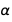
lebih dari untuk
.
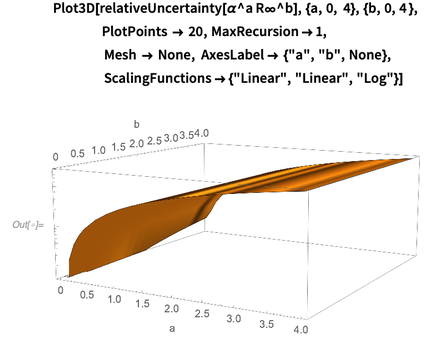
Di bawah ini adalah grafik kesalahan relatif log-base-10
sebagai fungsi
a dan
b . Jelas, untuk derajat kecil, kesalahan relatif produk lemah tergantung pada eksponen
a dan
b . Grafik ini menunjukkan bahwa ketergantungan kesalahan
mendominasi relatif terhadap (eksponen struktur halus). Pengamatan ini dijelaskan oleh fakta bahwa kesalahan konstanta Rydberg adalah 50 kali lebih kecil dari kesalahan konstanta struktur halus.
Untuk menghitung kesalahan berbagai konstanta di SI baru, kami akan menggunakan langkah-langkah berikut:
β’ Mengambil representasi yang setara untuk konstanta fisik yang dapat diakses dari kelas entitas
PhysicalConstant .
Persamaan identik antara konstanta fisik ini adalah hukum fisika dan karenanya harus dipertahankan dalam SI lama dan SI baru.
β’ Pikirkan rumus sebagai seperangkat persamaan aljabar yang dapat digunakan berbagai metode pengecualian untuk mengekspresikan konstanta melalui kombinasi tujuh konstanta dasar SI baru, serta konstanta struktur halus
dan konstanta Rydberg
.
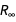
Ini adalah sembilan konstanta dasar yang kami izinkan untuk diterapkan dalam definisi setiap konstanta baru yang dipertimbangkan. (Secara teknis, ada 10 konstanta dalam daftar, tetapi karena hubungan penskalaan sederhana antara
h dan
β , sebenarnya ada sembilan konstanta βberbedaβ dalam daftar ini.)
Kelas entitas "
PhysicalConstant " berisi banyak informasi tentang hubungan antara konstanta fisik. Sebagai contoh, berikut adalah bentuk setara dari empat konstanta yang saat ini sedang diukur dan akan segera diidentifikasi memiliki nilai yang akurat.
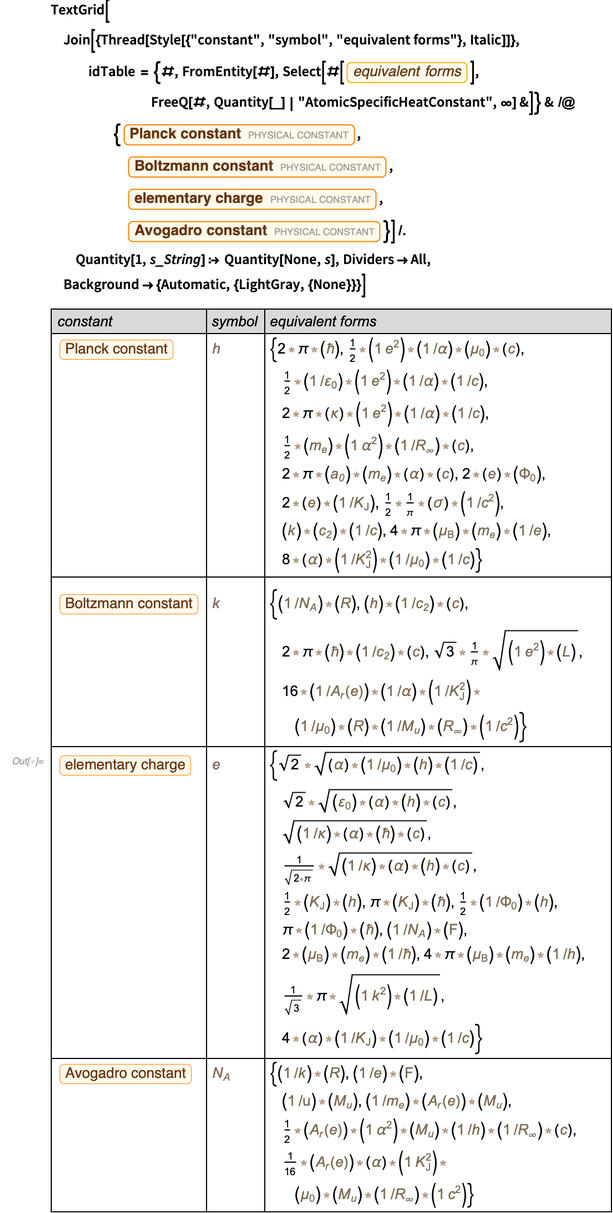
Dalam keakuratan nilai yang diukur, semua elemen unit ini bekerja sekarang. Inilah pemeriksaan numerik cepat dari bentuk-bentuk alternatif konstanta Planck. Tetapi nilai numerik tertentu, terutama kesalahan, tergantung pada bentuk presentasi yang sebenarnya.
Around [], .
. .
, . , ? , , , , , .
, , ( ,
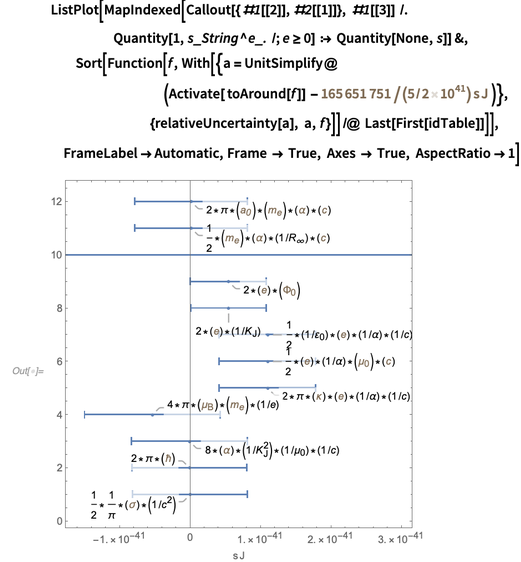
Entity [" PhysicalConstant",. ] dan dalam Kuantitas [ 1 ,. ] disamakan). Alasan kami menggunakan entitas, bukan kuantitas dalam perhitungan berikutnya, ada dua: pertama, entitas itu nyaman, representasi mudah dibaca; dan kedua, fungsi aljabar (seperti GroebnerBasis ) tidak menembus kuantitas untuk menentukan sifat argumen pertama mereka.
Lalu kami membuat semua identitas polinomial. Langkah terakhir berarti: (1) mengurangi sisi kiri dari sisi kanan; dan (2) bahwa tidak ada kekuatan fraksional (mis., akar kuadrat) dari konstanta tidak lagi muncul. Kami melakukan transformasi sedemikian menjadi polinomial dengan mencari semua eksponen fraksional dan menemukan LCM (faktor umum terkecil) dari semua penyebutnya.
Di bawah ini adalah salah satu persamaan sebelumnya yang berisi konstanta dengan kekuatan fraksional.
Setelah polinomisasi, kita sampai pada polinomial beberapa variabel dalam tiga konstanta yang ada. Polinomial ini harus dihilangkan.
Tabel berikut menunjukkan bagaimana fungsi
toPolynomial berlaku untuk bentuk-bentuk setara yang ditunjukkan sebelumnya untuk muatan dasar. Setelah kanonisasi β di
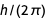
, beberapa polinomial yang dihasilkan menjadi identik.
Sekarang, berdasarkan konstanta fisik yang tersedia (tanpa konstanta yang digunakan dalam menentukan SI baru), kami mendapatkan cukup bentuk yang setara untuk membuat satu set persamaan.
Di bawah ini adalah daftar persamaan polinom yang diperoleh untuk ekspresi muatan dasar.
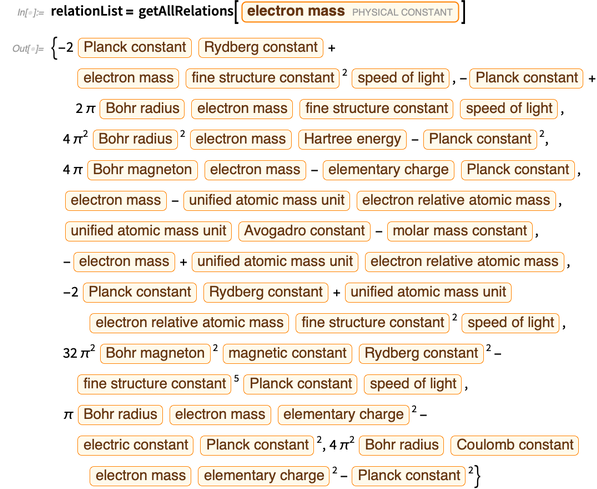
Kami menyatakan semua kesalahan melalui kesalahan
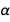
dan
. Hanya dua konstanta ini yang cukup untuk mengekspresikan kesalahan dari banyak konstanta fisik. Dan karena kesalahan mereka saling independen, dan karena kesalahannya cukup kecil, kedua konstanta yang cukup terkenal ini paling cocok untuk mengekspresikan versi baru dari banyak konstanta fisik yang dioptimalkan (dalam arti kesalahan). Dan, tentu saja, kami mengizinkan ketujuh konstanta yang tepat dari SI baru; karena jumlah yang akurat, keberadaan mereka tidak akan mengubah kesalahan.
Pekerjaan utama pada ekspresi konstanta yang diberikan dalam hal konstanta SI dan
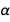
dan
akan diimplementasikan oleh fungsi
GroebnerBasis . Mengatur
MonomialOrder -> parameter ElventionOrder adalah langkah penting yang menghilangkan semua kuantitas fisik "yang tidak perlu", meninggalkan satu persamaan polinomial dengan konstanta yang ditentukan secara tepat dan (jika perlu) struktur halus dan konstanta Rydberg.
Dengan menghilangkan konstanta yang diikat oleh massa elektron, kita memperoleh
.
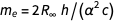
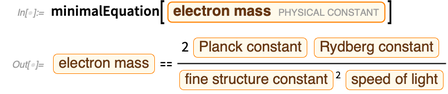
Kesalahan ungkapan ini muncul dari istilah tersebut
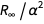
. Kita dapat mendefinisikan fungsi yang menghapus anggota
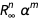
menyebabkan kesalahan.
Untuk representasi yang lebih ringkas, kita bisa mendefinisikan fungsi yang mengembalikan bentuk yang setara, serta kesalahan lama dan baru - dalam bentuk string.
Kami mengakhiri blog dengan menyajikan tabel kesalahan lama dan baru untuk lebih dari selusin konstanta fisik. Daftar ini dipilih sebagai contoh representatif; konstanta lain dapat diproses dengan cara yang sama (ini mungkin memerlukan penambahan konstanta tidak akurat tambahan untuk konservasi, seperti konstanta gravitasi atau parameter dari model standar).
Menggabungkan baris dalam tabel memberikan hasil berikut untuk representasi optimal dari konstanta ini dalam sistem unit SI baru.
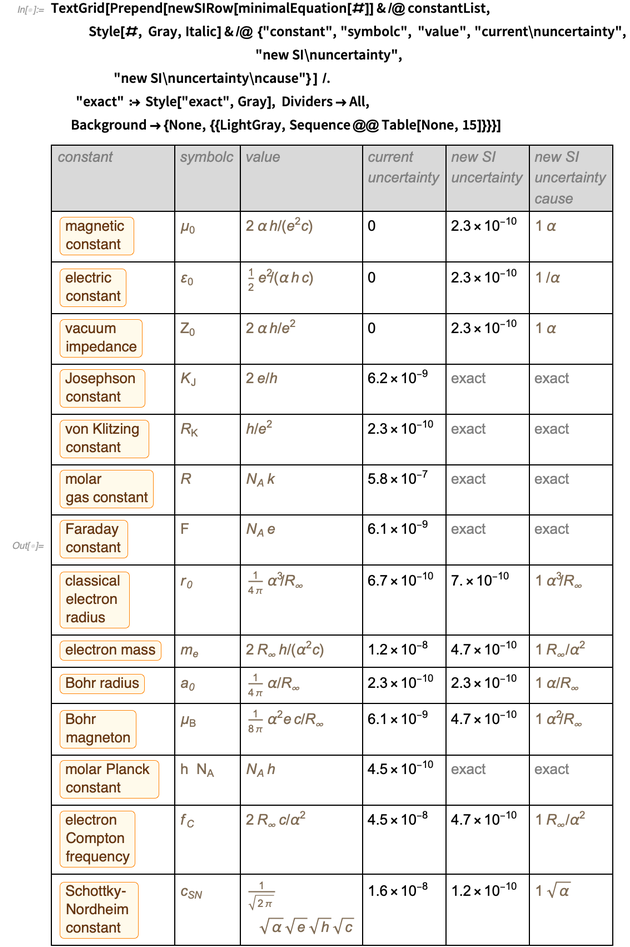
Itu adalah tabel yang ingin kami tampilkan, dan kami berhasil menampilkannya. Perhatikan penampilannya
dalam pembilang dan penyebut
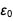
dan
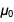
sehingga setelah dikurangi hasilnya
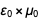
menjadi
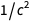
. Daftar serupa dapat ditemukan di bagian bawah halaman Wikipedia tentang
mendefinisikan ulang unit SI .
Sekarang kita dapat dengan tenang mengharapkan
Hari Metrologi Dunia 2019 untuk dunia yang secara fundamental lebih baik, dijelaskan melalui konstanta fundamental.
Unduh Blog
Notebook Wolfram .
Sistem Wolfram Mathematica gratis sementaraPunya pertanyaan? Info kontak-russia@wolfram.com