🛅 🍀 🌠 Analisis wavelet Bagian 1 👌🏻 🚃 ⬇️

Pendahuluan

Pertimbangkan transformasi wavelet diskrit (DWT) diimplementasikan di perpustakaan PyWavelets PyWavelets 1.0.3 . PyWavelets adalah perangkat lunak sumber terbuka gratis yang dirilis di bawah lisensi MIT.

Saat memproses data pada komputer, versi diskrit dari transformasi wavelet kontinu dapat dilakukan, dasar-dasarnya dijelaskan dalam artikel saya sebelumnya. Namun, menentukan nilai diskrit dari parameter (a, b) dari wavelet dengan langkah acak arbita dan Δb membutuhkan sejumlah besar perhitungan.

Selain itu, hasilnya adalah jumlah koefisien yang berlebihan, jauh melebihi jumlah sampel dari sinyal asli, yang tidak diperlukan untuk rekonstruksinya.

Discrete wavelet transform (DWT) yang diimplementasikan di perpustakaan PyWavelets memberikan informasi yang cukup baik untuk analisis sinyal dan untuk sintesisnya, sementara menjadi ekonomis dalam hal jumlah operasi dan memori yang diperlukan.

Kapan harus menggunakan transformasi wavelet alih-alih transformasi Fourier

Transformasi Fourier akan bekerja dengan baik ketika spektrum frekuensi stasioner. Dalam hal ini, frekuensi yang ada dalam sinyal tidak tergantung pada waktu, dan sinyal tersebut mengandung frekuensi xHz yang ada di mana saja dalam sinyal. Semakin goyah sinyalnya, semakin buruk hasilnya. Ini adalah masalah, karena sebagian besar sinyal yang kita lihat dalam kehidupan nyata tidak stabil.

Transformasi Fourier memiliki resolusi tinggi dalam domain frekuensi, tetapi resolusi nol dalam domain waktu. Kami menunjukkan ini dalam dua contoh berikut.

Daftar

import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # 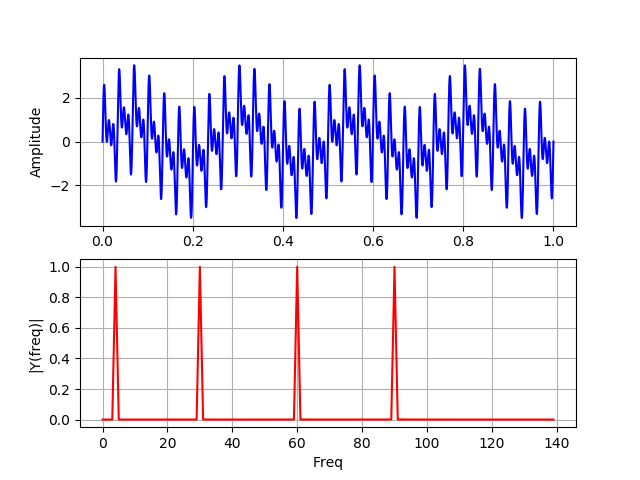sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y= y1a + y2a + y3a + y4a spectrum_wavelet(y) show()

Pada grafik ini, keempat frekuensi hadir dalam sinyal selama seluruh waktu operasinya.

Daftar

 import numpy as np from scipy import fftpack from pylab import* N=100000 dt = 1e-5 xa = np.linspace(0, 1, num=N) xb = np.linspace(0, 1/4, num=N/4) frequencies = [4, 30, 60, 90] y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb) y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb) y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb) y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb) def spectrum_wavelet(y): Fs = 1 / dt # 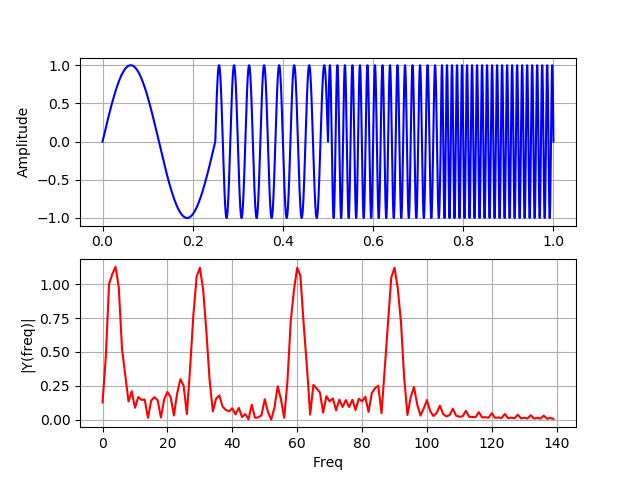sampling rate, Fs = 0,1 MHz n = len(y) # length of the signal k = np.arange(n) T = n / Fs frq = k / T # two sides frequency range frq = frq[range(n // 2)] # one side frequency range Y = fftpack.fft(y) / n # fft computing and normalization Y = Y[range(n // 2)] / max(Y[range(n // 2)]) # plotting the data subplot(2, 1, 1) plot(k/N , y, 'b') ylabel('Amplitude') grid() # plotting the spectrum subplot(2, 1, 2) plot(frq[0:140], abs(Y[0:140]), 'r') xlabel('Freq') plt.ylabel('|Y(freq)|') grid() y = np.concatenate([y1b, y2b, y3b, y4b]) spectrum_wavelet(y) show()

Pada grafik ini, sinyal tidak tumpang tindih dalam waktu, lobus samping disebabkan oleh kesenjangan antara empat frekuensi yang berbeda.

Untuk dua spektrum frekuensi yang mengandung empat puncak yang persis sama, transformasi Fourier tidak dapat menentukan di mana frekuensi ini hadir dalam sinyal. Pendekatan terbaik untuk menganalisis sinyal dengan spektrum frekuensi dinamis adalah transformasi wavelet.

Sifat utama wavelet

Pilihan jenis, dan oleh karena itu sifat-sifat wavelet, tergantung pada tugas analisis, misalnya, untuk menentukan nilai efektif arus dalam industri tenaga listrik, bentuk gelombang urutan yang lebih tinggi dari Ingrid Daubechies memberikan akurasi yang lebih besar. Properti wavelet dapat diperoleh menggunakan fungsi pywt.DiscreteContinuousWavelet () dalam daftar berikut:

Daftar

 import pywt from pylab import * from numpy import * discrete_wavelets = ['db5', 'sym5', 'coif5', 'haar'] print('discrete_wavelets-%s'%discrete_wavelets ) st='db20' wavelet = pywt.DiscreteContinuousWavelet(st) print(wavelet) i=1 phi, psi, x = wavelet.wavefun(level=i) subplot(2, 1, 1) title("   -  -%s"%st) plot(x,psi,linewidth=2, label='level=%s'%i) grid() legend(loc='best') subplot(2, 1, 2) title("  - -%s"%st) plt.plot(x,phi,linewidth=2, label='level=%s'%i) legend(loc='best') grid() show()

Kami mendapatkan:

discrete_wavelets - ['db5', 'sym5', 'coif5', 'haar']

 Wavelet db20 Family name: Daubechies Short name: db Filters length: 40 Orthogonal: True Biorthogonal: True Symmetry: asymmetric DWT: True CWT: False

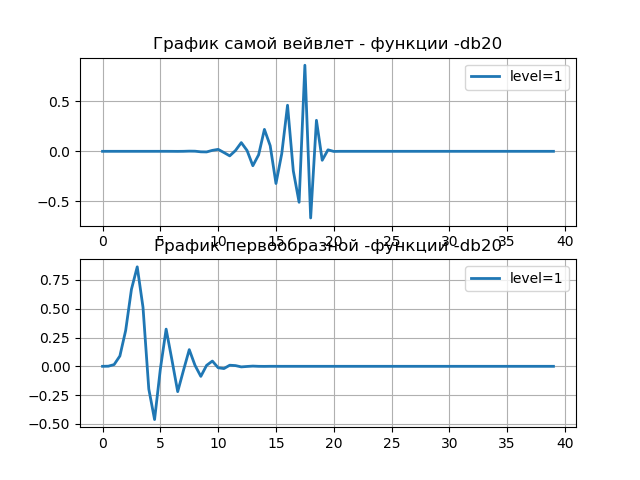
Dalam sejumlah kasus praktis, menjadi perlu untuk memperoleh informasi tentang frekuensi pusat wavelet psi, fungsi yang digunakan, misalnya, dalam analisis wavelet sinyal untuk mendeteksi cacat pada roda gigi:

 import pywt f=pywt.central_frequency('haar', precision=8 ) print(f) #  : scale=1 f1=pywt.scale2frequency('haar',scale) print(f1)

 0.9961089494163424 0.9961089494163424

Menggunakan frekuensi pusat

f_{c}

$f_ {c}$ wavelet ibu dan faktor skala "a" dapat mengubah skala menjadi frekuensi semu

f_{a}

$f_ {a}$ menggunakan persamaan:

f_{a} = f r a c f_{c} a

$f_ {a} = \ frac {f_ {c}} {a}$

Mode Ekstensi Sinyal

Sebelum menghitung transformasi wavelet diskrit menggunakan bank filter , perlu memperpanjang sinyal . Tergantung pada metode ekstrapolasi, artefak yang signifikan dapat terjadi pada batas sinyal, yang menyebabkan ketidakakuratan dalam transformasi DWT.

PyWavelets menyediakan beberapa teknik ekstrapolasi sinyal yang dapat digunakan untuk meminimalkan efek negatif ini. Untuk menunjukkan metode seperti itu, gunakan daftar berikut:

Mendaftar demonstrasi metode ekstensi sinyal

 import numpy as np from matplotlib import pyplot as plt from pywt._doc_utils import boundary_mode_subplot # synthetic test signal x = 5 - np.linspace(-1.9, 1.1, 9)**2 # Create a figure with one subplots per boundary mode fig, axes = plt.subplots(3, 3, figsize=(10, 6)) plt.subplots_adjust(hspace=0.5) axes = axes.ravel() boundary_mode_subplot(x, 'symmetric', axes[0], symw=False) boundary_mode_subplot(x, 'reflect', axes[1], symw=True) boundary_mode_subplot(x, 'periodic', axes[2], symw=False) boundary_mode_subplot(x, 'antisymmetric', axes[3], symw=False) boundary_mode_subplot(x, 'antireflect', axes[4], symw=True) boundary_mode_subplot(x, 'periodization', axes[5], symw=False) boundary_mode_subplot(x, 'smooth', axes[6], symw=False) boundary_mode_subplot(x, 'constant', axes[7], symw=False) boundary_mode_subplot(x, 'zeros', axes[8], symw=False) plt.show()

Grafik menunjukkan bagaimana sinyal pendek (merah) mengembang (hitam) di luar panjang aslinya.

Transformasi Wavelet Diskrit

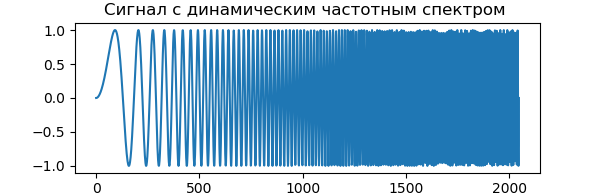
Untuk menunjukkan DWT, kami akan menggunakan sinyal dengan spektrum frekuensi dinamis, yang meningkat seiring waktu. Awal sinyal berisi nilai frekuensi rendah, dan ujung sinyal berisi frekuensi rentang gelombang pendek. Ini memungkinkan kita untuk dengan mudah menentukan bagian mana dari spektrum frekuensi yang disaring dengan hanya melihat sumbu waktu:

Daftar

 from pylab import * from numpy import* x = linspace(0, 1, num=2048) chirp_signal = sin(250 * pi * x**2) fig, ax = subplots(figsize=(6,1)) ax.set_title("     ") ax.plot(chirp_signal) show()

Transformasi wavelet diskrit dalam PyWavelets 1.0.3 adalah fungsi pywt.dwt (), yang menghitung koefisien pendekatan cA dan koefisien detail cD dari transformasi wavelet level pertama dari sinyal yang ditentukan oleh vektor:

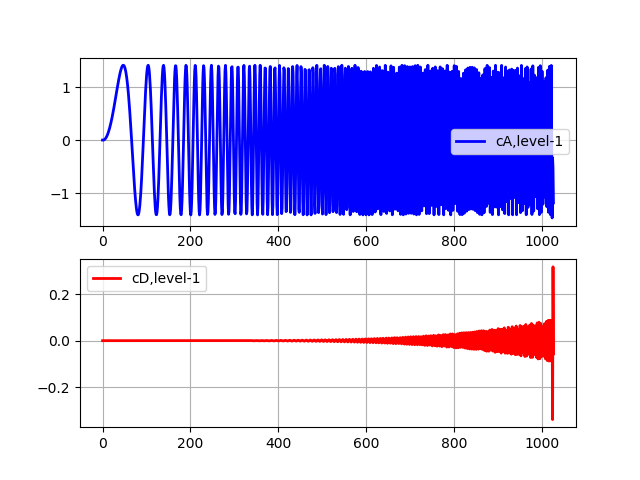
Daftar Tingkat Satu Transformasi

 import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-1') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-1') grid() legend(loc='best') show()

Daftar Level 5 Transformasi

 import pywt from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' (cA, cD) = pywt.dwt(y,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) (cA, cD) = pywt.dwt(cA,st) subplot(2, 1, 1) plot(cA,'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(cD,'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()

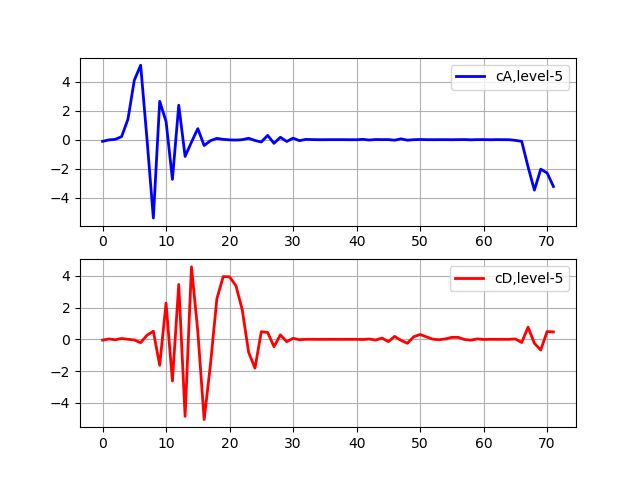
Koefisien aproksimasi (cA) merepresentasikan output dari low-pass filter (rata-rata filter) DWT. Koefisien detail (cD) merepresentasikan output dari filter high-pass (filter diferensial) DWT.

Anda dapat menggunakan fungsi pywt.wavedec () untuk segera menghitung koefisien level yang lebih tinggi. Fungsi ini mengambil sinyal dan level input sebagai input dan mengembalikan satu set koefisien perkiraan (level ke-n) dan n set koefisien detail (dari level 1 ke level ke-ke-1). Berikut ini adalah contoh untuk tingkat kelima:

 from pywt import wavedec from pylab import * from numpy import * x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=5) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-5') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-5') grid() legend(loc='best') show()

Hasilnya, kami mendapatkan grafik yang sama seperti pada contoh sebelumnya. Koefisien cA dan cD dapat diperoleh secara terpisah:

Untuk ca:

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1)

Untuk cD:

 import pywt from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data = sin (250 * pi * x**2) coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1)

Filter bank

Beberapa masalah yang terkait dengan tingkat konversi dibahas di bagian sebelumnya. Namun, DWT selalu diimplementasikan sebagai bank filter dalam bentuk kaskade filter high-pass dan low-pass. Filter bank adalah cara yang sangat efektif untuk membagi sinyal menjadi beberapa sub-band frekuensi.

Pada tahap pertama dengan skala kecil, menganalisis perilaku frekuensi tinggi dari sinyal. Pada tahap kedua, skala meningkat dengan faktor dua (frekuensi berkurang dengan faktor dua), dan kami menganalisis perilaku sekitar setengah frekuensi maksimum. Pada tahap ketiga, faktor skala adalah empat, dan kami menganalisis perilaku frekuensi sekitar seperempat dari frekuensi maksimum. Dan ini berlanjut sampai kita mencapai tingkat dekomposisi maksimum.

Level dekomposisi maksimum dapat dihitung menggunakan fungsi pywt.wavedec (), sedangkan dekomposisi dan detail akan terlihat seperti:

Daftar

 import pywt from pywt import wavedec from pylab import * from numpy import* x = linspace (0, 1, num = 2048) data= sin (250 * pi * x**2) n_level=pywt.dwt_max_level(len(data), 'sym5') print('  : %s'%n_level) x = linspace (0, 1, num = 2048) y = sin (250 * pi * x**2) st='sym5' coeffs = wavedec(y, st, level=7) subplot(2, 1, 1) plot(coeffs[0],'b',linewidth=2, label='cA,level-7') grid() legend(loc='best') subplot(2, 1, 2) plot(coeffs[1],'r',linewidth=2, label='cD,level-7') grid() legend(loc='best') show()

Kami mendapatkan:

Level dekomposisi maksimum: 7

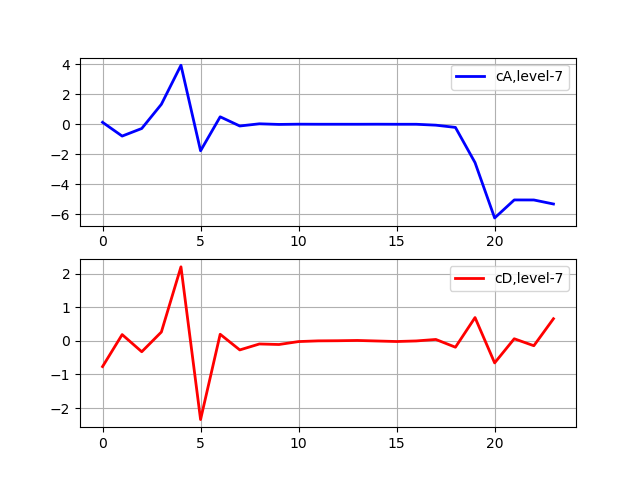
Dekomposisi berhenti ketika sinyal menjadi lebih pendek dari panjang filter untuk wavelet sym5 yang diberikan. Sebagai contoh, misalkan kita memiliki sinyal dengan frekuensi hingga 1000 Hz. Pada tahap pertama, kami memisahkan sinyal kami menjadi bagian frekuensi rendah dan frekuensi tinggi, mis. 0-500 Hz dan 500-1000 Hz. Pada tahap kedua, kami mengambil bagian frekuensi rendah dan membaginya lagi menjadi dua bagian: 0-250 Hz dan 250-500 Hz. Pada tahap ketiga, kami membagi bagian 0-250 Hz menjadi bagian 0-125 Hz dan bagian 125-250 Hz. Ini berlanjut sampai kita mencapai tingkat dekomposisi maksimum.

Analisis file wav menggunakan fft Fourier dan skalog wavelet

Untuk analisis, gunakan file WebSDR . Pertimbangkan analisis sinyal tereduksi menggunakan triang dari scipy.signal dan implementasi transformasi Fourier diskrit dalam python (fft from scipy.fftpack). Jika panjang urutan fft tidak sama dengan 2n, maka alih-alih transformasi Fourier cepat (fft), transformasi Fourier diskrit (dft) akan dilakukan. Beginilah cara tim ini bekerja.

Kami menggunakan buffer transformasi Fourier cepat sesuai dengan skema berikut (data numerik misalnya):

fftbuffer = np.zeros (15); buat buffer yang diisi dengan nol;
fftbuffer [: 8] = x [7:]; pindahkan ujung sinyal ke bagian pertama buffer; fftbuffer [8:] = x [: 7] —kami memindahkan awal sinyal ke bagian terakhir buffer; X = fft (fftbuffer) - kami mempertimbangkan transformasi Fourier dari buffer yang diisi dengan nilai sinyal.

Untuk membuat spektrum fase lebih mudah dibaca, penyebaran fase berlaku. Untuk melakukan ini, ubah baris dengan perhitungan karakteristik fase: pX = np.unwrap (np.angle (X)).

Daftar untuk analisis fragmen sinyal fft

 import numpy as np from pylab import * from scipy import * import scipy.io.wavfile as wavfile M=501 hM1=int(np.floor((1+M)/2)) hM2=int(np.floor(M/2)) (fs,x)=wavfile.read('WebSDR.wav') x1=x[5000:5000+M]*np.hamming(M) N=511 fftbuffer=np.zeros([N]) fftbuffer[:hM1]=x1[hM2:] fftbuffer[N-hM2:]=x1[:hM2] X=fft(fftbuffer) mX=abs(X) pX=np.angle(X) suptitle(" WebSDR") subplot(3, 1, 1) st='  (WebSDR.wav)' plot(x,linewidth=2, label=st) legend(loc='center') subplot(3, 1, 2) st='    ' plot(mX,linewidth=2, label=st) legend(loc='best') subplot(3, 1, 3) st='    ' pX=np.unwrap(np.angle(X)) plot(pX,linewidth=2, label=st) legend(loc='best') show()

Untuk analisis komparatif, kita akan menggunakan skalogram wavelet yang dapat dibangun menggunakan fungsi tree = pywt.wavedec (sinyal, 'coif5') di matplotlib.

Daftar Skalog Wavelet

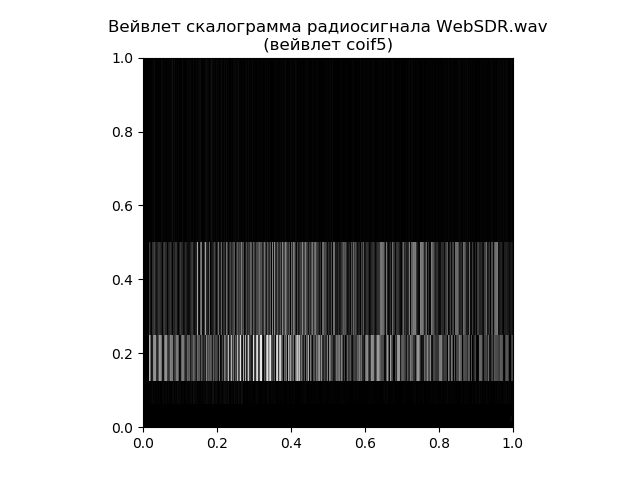
 from pylab import * import pywt import scipy.io.wavfile as wavfile #     ,     . def lepow2(x): return int(2 ** floor(log2(x))) #    MRA. def scalogram(data): bottom = 0 vmin = min(map(lambda x: min(abs(x)), data)) vmax = max(map(lambda x: max(abs(x)), data)) gca().set_autoscale_on(False) for row in range(0, len(data)): scale = 2.0 ** (row - len(data)) imshow( array([abs(data[row])]), interpolation = 'nearest', vmin = vmin, vmax = vmax, extent = [0, 1, bottom, bottom + scale]) bottom += scale #  ,   . rate, signal = wavfile.read('WebSDR.wav') signal = signal[0:lepow2(len(signal))] tree = pywt.wavedec(signal, 'coif5') gray() scalogram(tree) show()

Dengan demikian, skalogram memberikan jawaban yang lebih rinci untuk pertanyaan distribusi frekuensi dari waktu ke waktu, dan transformasi Fourier yang cepat bertanggung jawab atas frekuensi itu sendiri. Itu semua tergantung pada tugas, bahkan untuk contoh sederhana seperti itu.

Kesimpulan

Alasan untuk menggunakan transformasi wavelet diskrit untuk sinyal dinamis diberikan.
Contoh analisis wavelet menggunakan PyWavelets 1.0.3, perangkat lunak open source gratis yang dirilis di bawah lisensi MIT, disediakan.
Perangkat lunak untuk penggunaan praktis perpustakaan PyWavelets dipertimbangkan.

Analisis wavelet Bagian 1

Pendahuluan

Kapan harus menggunakan transformasi wavelet alih-alih transformasi Fourier

Sifat utama wavelet

Mode Ekstensi Sinyal

Transformasi Wavelet Diskrit

Filter bank

Analisis file wav menggunakan fft Fourier dan skalog wavelet

Kesimpulan

More articles: