Geekly articles weekly

Julia dalam labirin


Mengurai satu masalah olimpiade, kita akan menyusuri koridor berkelok-kelok generasi labirin dan bagian mereka, dan kita juga akan melihat bahwa dalam bahasa Julia kesederhanaan implementasi algoritma yang berbatasan dengan kode pseudo mereka.


Tantangan


Labirin adalah kotak kotak 10 dengan 10, di beberapa sel ada hambatan, dan di satu sel ada jalan keluar. Robot berada dalam labirin seperti itu dan dapat melakukan 4 perintah: gerakkan satu sel ke bawah, atas, kanan atau kiri. Jika robot mencoba untuk melampaui batas-batas labirin atau pergi ke kandang dengan penghalang, maka ia tetap di tempatnya. Jika robot memasuki pintu keluar, maka ia keluar dari labirin dan mengabaikan perintah lebih lanjut. Tulis sebuah program untuk robot, yang mengeksekusi robot mana saja yang keluar, terlepas dari sel di mana ia berada di awal. Program harus terdiri dari tidak lebih dari 1000 tim.



Format input


Tidak ada entri. Anda perlu menulis sebuah program untuk satu kondisi spesifik yang ditentukan
labirin.
Versi labirin yang bisa Anda salin. 0 - sel bebas, 1 - hambatan, x -
jalan keluar


0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000

Format output


Satu baris terdiri dari karakter U, D, R, L dengan panjang tidak lebih dari 1000


Persiapan


Mereka yang tidak bekerja dengan grafik di Julia perlu mengunduh paket


 using Pkg Pkg.add("Plots") Pkg.add("Colors") Pkg.add("Images") Pkg.build("Images") #

Paling nyaman bekerja di Jupyter, karena gambar-gambar akan ditampilkan secara langsung selama bekerja. Di sini Anda dapat menemukan tentang instalasi, serta pengantar dan tugas untuk pemula.


Dalam kondisi tugas kami ada versi labirin untuk menyalin


 S0 = "0011010011 0100001000 0110x00000 0010000100 0000111000 0000100100 0000010010 0100101010 0011001010 1000011000"

Untuk menggambar labirin, Anda perlu membuat matriks. Karena kami tidak ingin menempatkan spasi secara manual, kami akan bekerja dengan garis:


 S1 = prod(s-> s*' ', '['*S0*']') # prod(fun, arr)    arr #     fun #  julia  *   "[ 0 0 1 1 0 1 0 0 1 1 \n 0 1 0 0 0 0 1 0 0 0 \n 0 1 1 0 x 0 0 0 0 0 \n 0 0 1 0 0 0 0 1 0 0 \n 0 0 0 0 1 1 1 0 0 0 \n 0 0 0 0 1 0 0 1 0 0 \n 0 0 0 0 0 1 0 0 1 0 \n 0 1 0 0 1 0 1 0 1 0 \n 0 0 1 1 0 0 1 0 1 0 \n 1 0 0 0 0 1 1 0 0 0 ] "

Mengganti huruf canggung x dengan angka dan mengurai string, kita mendapatkan matriks integer yang mendefinisikan labirin kita. Kemudian, untuk kenyamanan yang lebih besar, ubah yang ke nol, dan nol menjadi yang, dan tutup labirin dengan dinding:


 S2 = replace(S1, 'x'=>'9') M0 = S2 |> Meta.parse |> eval m,n = size(M0) M1 = replace(M0, 1=>0, 0=>1) M = zeros(Int64,m+2,n+2) for i in 2:m+1, j in 2:n+1 M[i,j] = M1[i-1,j-1] end M # Maze map matrix 12×12 Array{Int64,2}: 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0

Dalam matriks


 length(M) 144

sel dan dari mereka


 sum(M)-9 70

di mana Anda dapat berjalan, yaitu - posisi awal yang potensial. Anda dapat menampilkan hasilnya dengan membuat histogram dua dimensi


 using Plots heatmap(M, yaxis = :flip) # flip -


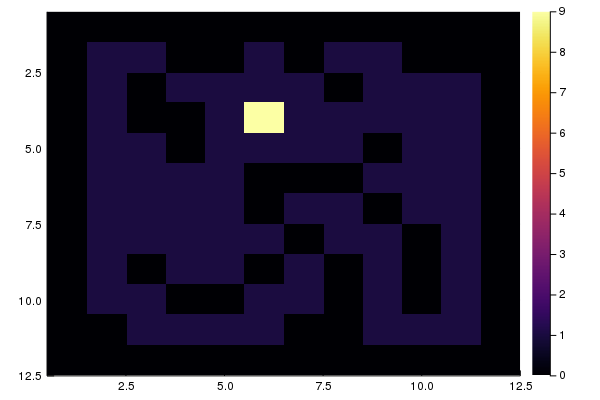
Verifikasi Solusi


Pertama-tama, Anda perlu memikirkan prosedur yang akan memverifikasi kebenaran solusi yang diusulkan. Atur tipe komposit Point untuk menggunakan terminologi titik dan koordinat:


 mutable struct Point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end

Dan sekarang Anda perlu belajar bagaimana menerjemahkan urutan perintah yang dapat dimengerti oleh robot menjadi kode.


Idenya cukup sederhana: ada koordinat awal, sebuah garis muncul dengan algoritma yang memberitahu cara berjalan. Kami mengambil satu huruf dan melihat sel mana yang akan diinjak. Untuk koordinat saat ini kami menambahkan nilai yang disimpan dalam sel ini. Artinya, jika ada nol (dinding), kita belum bergerak ke mana pun, kalau tidak kita telah mengambil langkah kecil ke arah yang diperlukan.


Dengan menggunakan kekuatan metaprogramming, Anda dapat mengganti urutan arah yang masuk dengan kode besar yang seragam dan menjalankannya


 S = "RRLDUURULDDRDDRRRUUU" S1 = replace(S , "R"=>"c.y+=M[cx, c.y+1];") S1 = replace(S1, "L"=>"cy-=M[cx, cy-1];") S1 = replace(S1, "U"=>"c.x+=M[c.x+1, cy];") S1 = replace(S1, "D"=>"cx-=M[cx-1, cy];") #  - start point Sp = eval( Meta.parse(S1) )

Tetapi metode ini memiliki sejumlah ketidaknyamanan, oleh karena itu, kami akan menggunakan operator kondisional klasik. Ngomong-ngomong, fakta bahwa output ditunjukkan oleh angka 9 adalah trik kecil: agar tidak memeriksa setiap sel, dan apakah itu jalan keluar, kami memulai gerakan dengan menambahkan nilai yang disimpan dalam sel tertentu. Ketika robot melangkah ke pintu keluar, sejumlah besar sengaja ditambahkan ke koordinatnya, sehingga robot terbang di luar batas array, yang dapat ditangkap sebagai kesalahan menggunakan blok:


 try #     catch #       end

Jadi, kami mengimplementasikan fungsi yang akan memeriksa apakah robot mencapai jalan keluar mulai dari titik c menjalankan perintah dari string str :


 function isexit(str, c) scatter!([cy],[cx]) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end

Mari kita kumpulkan fungsi yang akan mengulangi semua posisi awal


 function test(Str) k = 0 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end

Periksa perintah:


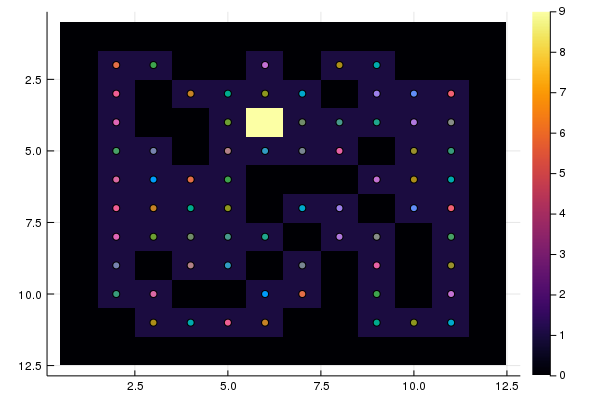
 S = "RRRLDUUURRRUUURRRRLLLRRUULDDDDRRRRDDDRRRUUU" heatmap(M, yaxis = :flip) test(S) # 10 test completed from 70 plot!(legend = false)


Semua titik awal diuji, dan hanya 10 yang mengarah ke pintu keluar. Penting untuk membangun rute dari setiap titik ke pintu keluar.


Sebelum menyelam ke dalam generasi dan perjalanan labirin, kami akan menyimpan hasil kami. Kami akan menggunakan paket Images.jl yang menyediakan banyak kemungkinan di bidang pemrosesan gambar ( contoh yang baik ). Salah satu alat pendukungnya adalah paket Colors.jl , yang memperluas kemampuan Julia untuk bekerja dengan warna.


 using Images clrs(x) = x==9 ? RGB(1.,0.5,0) : RGB(x,x,x) maze = clrs.(M) # maze = Gray.(maze) # save("D:/dat/maze12x12.png", maze)


Pencarian Kedalaman


Menerapkan gagasan dari sebuah artikel tentang Habr .
Idenya sederhana: buat kisi-kisi dinding


 M = 10 N = 10 A = [ i&j&1 for i in 0:N, j in 0:M ] # isodd(i) & isodd(j) & 1 Gray.(A) # from Images.jl


kemudian, melalui perulangan, kami menerobos rute dan cabang. Kami mendefinisikan fungsi yang menemukan daerah tetangga yang belum dikunjungi (kami akan menunjuknya, katakanlah, dengan deuce) dan mengembalikan salah satu tetangga ini (jika tidak ada tetangga yang belum dikunjungi, ia mengembalikan titik bendera):


 function neighbours2(A,p, n, m) nbrs = [Point(px, p.y+2), # up Point(px, py-2), # down Point(px-2, py), # left Point(p.x+2, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==2 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(-1,-1) end

Kami akan memecahkan dinding seperti ini:


 function breakwall(A, newp,oldp) #  : x = (newp.x + oldp.x) >> 1 #   y = (newp.y + oldp.y) >> 1 A[x,y] = 1 end

Algoritma


  1. Jadikan sel awal aktif dan tandai sebagai dikunjungi.
  2. Meskipun ada sel yang belum dikunjungi
    1. Jika sel saat ini memiliki "tetangga" yang belum dikunjungi
    1. Dorong sel saat ini ke tumpukan
    2. Pilih sel acak dari tetangga
    3. Lepaskan dinding antara sel saat ini dan yang dipilih
    4. Jadikan sel yang dipilih saat ini dan tandai sebagai dikunjungi.
    2. Sebaliknya, jika tumpukan tidak kosong
    1. Tarik sangkar keluar dari tumpukan
    2. Jadikan ini terkini
    3. Sebaliknya
    1. Pilih sel yang belum dikunjungi secara acak, buat yang sekarang dan tandai sebagai yang dikunjungi.

Kode program
 function amazeng(n, m) M = [ 2(i&j&1) for i in 0:n, j in 0:m ]; p = Point(2,2) #   lifo = [] #   push!(lifo, p) #i = 0 while length(lifo) != 0 #     M[px,py] = 1 #     np = neighbours2(M, p, n, m) # new point #    -   if np.x == np.y == -1 p = pop!(lifo) else push!(lifo, p) breakwall(M, np, p) p = np #i+=1 #maze = Gray.(M/2) #save("D:/dat/maze$i.png", maze) end end M[1,2] = 1 #  M[n,m+1] = 1 #  Gray.(M) end 

 lbrnt = amazeng(36, 48) # save("D:/dat/maze111.png", lbrnt)



Algoritma pencarian jalur lacak mundur:


  1. Jadikan sel awal aktif dan tandai sebagai dikunjungi.
  2. Sampai suatu solusi ditemukan
    1. Jika sel saat ini memiliki "tetangga" yang belum dikunjungi
    1. Dorong sel saat ini ke tumpukan
    2. Pilih sel acak dari tetangga
    3. Jadikan sel yang dipilih saat ini dan tandai sebagai dikunjungi.
    2. Sebaliknya, jika tumpukan tidak kosong
    1. Tarik sangkar keluar dari tumpukan
    2. Jadikan ini terkini
    3. Kalau tidak, tidak ada jalan keluar.

Kami mencari tetangga sebaliknya dan dalam radius satu sel, dan tidak melalui satu:


 function neighbours1(A, p, n, m) nbrs = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right goal = [] for a in nbrs if 0<ax<=n && 0<ay<=m && A[ax,ay]==1 push!(goal, a) end end length(goal) != 0 ? rand(goal) : Point(0,0) end

Tetapkan algoritma untuk melewati labirin dengan menggambar rute dan upaya yang gagal


 function amazeng(img, start, exit) M = Float64.(channelview(img)) n, m = size(M) p = start M[exit.x,exit.y] = 1 lifo = [] push!(lifo, p) while px != exit.x || py != exit.y M[px,py] = 0.4 np = neighbours1(M, p, n, m) if np.x == np.y == 0 M[px,py] = 0.75 p = pop!(lifo) #  -  ,    #      else push!(lifo, p) p = np end end Gray.(M) end

Seperti yang beberapa orang perhatikan, sebuah fungsi juga disebut, seperti yang dihasilkan oleh algoritma (Penjadwalan Berganda). Ketika Anda menyebutnya dengan dua angka, itu akan berhasil dengan metode membangun labirin, tetapi jika Anda menyebutnya dengan menentukan gambar dan dua titik (koordinat input dan output) sebagai argumen, maka pada output kita mendapatkan gambar dengan labirin melewati


 img0 = load("D:/dat/maze111.png") amazeng(img0)


Mari coba labirin kami:


 img0 = load("D:/dat/maze12x12.png") n, m = size(img0) amazeng(img0, Point(11,9), Point(4,6) )


Bahkan jika Anda memodifikasi fungsi sehingga rute diingat, algoritme masih terbukti tidak efektif karena ruang terbuka. Tapi labirin keluar dengan hebat.


Algoritma acak Prim


Segera setelah Anda mulai menggambar labirin, Anda tidak akan berhenti. Mari kita lakukan algoritma lain yang menarik:


  • Mulai dengan kisi-kisi penuh dinding.
  • Pilih sel, tandai sebagai bagian dari labirin. Tambahkan dinding sel ke daftar dinding.
  • Meskipun ada dinding dalam daftar:
    • Pilih dinding acak dari daftar. Jika hanya satu dari dua sel yang dibagi oleh dinding, maka:
      • Jadikan dinding sebagai bagian dan tandai sel yang belum dikunjungi sebagai bagian dari labirin.
      • Tambahkan dinding sel yang berdekatan ke daftar dinding.
    • Hapus dinding dari daftar.

Kode
 neighbors(p::Point) = [Point(px, p.y+1), # up Point(px, py-1), # down Point(px-1, py), # left Point(p.x+1, py)] # right function newalls!(walls, p, maze, n, m) nbrs = neighbors(p) for a in nbrs if 1<ax<n-1 && 1<ay<m-1 && !maze[ax,ay] push!(walls, a) #       . end end end function breakwall!(p, maze, n, m) nbrs = neighbors(p) #       if sum( a-> maze[ax,ay], nbrs) == 1 for a in nbrs if maze[ax,ay] # true =  px == ax ? nx = px : px>ax ? nx = p.x+1 : nx = px-1 py == ay ? ny = py : py>ay ? ny = p.y+1 : ny = py-1 maze[px,py] = true #   maze[nx,ny] = true px = nx py = ny return true end end else return false end end function prim(n, m) M = falses(n,m); #    p = Point(2, 2) M[px,py] = true walls = [] newalls!(walls, p, M, n, m) while length(walls) != 0 p = splice!( walls, rand(1:length(walls)) ) if breakwall!(p, M, n, m) newalls!(walls, p, M, n, m) end end M end 

 primaze = prim(19,19); Gray.(primaze)


Ternyata lebih bercabang dan tidak kalah mengagumkan, terutama proses perakitannya.


Dan sekarang kami menerapkan algoritma yang paling umum untuk menemukan rute terpendek:


Metode A *


  • 2 daftar simpul dibuat - tertunda dan sudah diulas. Titik awal ditambahkan ke yang tertunda, daftar yang ditinjau sejauh ini kosong.
  • Untuk setiap titik dihitung H- perkiraan jarak dari titik ke target.
  • Dari daftar poin untuk dipertimbangkan, poin dengan yang terkecil H. Biarkan dia X.
  • Jika X- tujuannya, lalu kami menemukan rute.
  • Kami bawa Xdari daftar yang tertunda ke daftar yang sudah ditinjau.
  • Untuk setiap titik yang berdekatan X(menunjukkan titik tetangga ini Y), lakukan hal berikut:
    • Jika Ysudah di tinjau - lewati saja.
    • Jika Ybelum ada dalam daftar tunggu - tambahkan di sana.
  • Jika daftar poin untuk dipertimbangkan kosong, tetapi kami belum mencapai tujuan, maka rute tidak ada.

Untuk memulai, mari kita mendefinisikan kelas "titik" yang akan tahu seberapa jauh dari target:


 mutable struct Point_h x::Int64 # horisont y::Int64 # vertical h::Float64 Point_h(x, y) = new(x, y, 0.) end

Sekarang kita mendefinisikan operasi perbandingan untuk struktur, metode untuk menetapkan keberadaan elemen dalam array, serta fungsi menghapus elemen, menemukan jarak antara titik dan daftar tetangga:


Terselip
 import Base: in, == ==(a::Point_h, b::Point_h) = ax==bx && ay==by function in(p::Point_h, Arr::Array{Point_h,1}) for a in Arr if a == p return true end end return false end function splicemin!(Arr)#::Array{Point_h,1} i = argmin( [ah for a in Arr] ) splice!(Arr, i) end dista(u,v) = hypot(vx-ux, vy-uy) # <=> sqrt( (vx-ux)^2 + (vy-uy)^2 ) neighbors(p::Point_h) = [Point_h(px, p.y+1), # up Point_h(px, py-1), # down Point_h(px-1, py), # left Point_h(p.x+1, py)] # right

Seperti biasa, operator tidak jelas dapat diklarifikasi menggunakan perintah ? mis. ?splice ?argmin .


Dan, sebenarnya, metode A * itu sendiri


Kode
 function astar(M, start, final) #   -       isgood(p) = 1<px<n && 1<py<m && M[px,py] != 0 n, m = size(M) #       start.h = dista(start,final) closed = [] opened = [] push!(opened, start) while length(opened) != 0 X = splicemin!(opened) if X in closed continue end if X == final break end push!(closed, X) nbrs = neighbors(X) ygrex = filter(isgood, nbrs) for Y in ygrex if Y in closed continue else Yh = dista(Y, final) push!(opened, Y) end end end #    closed # return end

Kami memuat gambar dengan labirin dan menyajikannya dalam bentuk matriks:


 img0 = load("D:/dat/maze0.png") mazematrix = Float64.(channelview(img0))

Dan kami membangun rute untuk keluar dari titik arbitrer:


 s = Point_h(11,9) # start f = Point_h(4,6) # finish M = copy(mazematrix) route = astar(M, s, f) i = 1 for c in route #   M[cx,cy] = 0.7 #save("D:/dat/Astar$i.png", M) i+=1 end Gray.(M)


Pencarian dari semua posisi terlihat seperti ini:



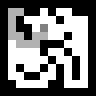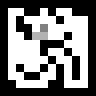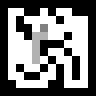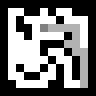
Terlihat agen itu bergegas selalu cenderung ke sisi pintu keluar dan sering berubah menjadi jalan buntu, yang menimbulkan langkah-langkah yang tidak perlu, dan seluruh rute diingat. Ini dihindari oleh versi algoritma A * yang sedikit lebih kompleks.


  • 2 daftar simpul dibuat - tertunda dan sudah diulas. Titik awal ditambahkan ke yang tertunda, daftar yang ditinjau sejauh ini kosong.
  • Untuk setiap titik dihitung F=G+H. G- jarak dari awal ke titik, H- perkiraan jarak dari titik ke target. Setiap titik juga menyimpan tautan ke titik asalnya.
  • Dari daftar poin untuk dipertimbangkan, poin dengan yang terkecil F. Biarkan dia X.
  • Jika X- tujuannya, lalu kami menemukan rute.
  • Kami bawa Xdari daftar yang tertunda ke daftar yang sudah ditinjau.
  • Untuk setiap titik yang berdekatan X(menunjukkan titik tetangga ini Y), lakukan hal berikut:
    • Jika Ysudah di tinjau - lewati saja.
    • Jika Ybelum ada dalam daftar tunggu - tambahkan di sana, mengingat tautan ke Xdan setelah dihitung Y.G(ini X.G+ jarak dari Xsebelumnya Y) dan Y.H.
    • Jika Ydalam daftar untuk dipertimbangkan - periksa apakah X.G+ jarak dari Xsebelumnya Y<Y.Gjadi kami sampai pada intinya Ycara yang lebih pendek, ganti Y.Gpada X.G+ jarak dari Xsebelumnya Y, dan titik dari mana mereka datang Ypada X.
  • Jika daftar poin untuk dipertimbangkan kosong, tetapi kami belum mencapai tujuan, maka rute tidak ada.

Tetapi bahkan dengan langkah-langkah yang tidak perlu, opsi kami berada dalam batasan tugas, jadi memodifikasi program akan menjadi pekerjaan rumah Anda.


Sampai akhir Olimpiade, tidak ada yang tersisa, tetapi kita masih perlu belajar bagaimana menerjemahkan hasil algoritme kita menjadi perintah dari bentuk "RRLUUDL..."


Dan setelah semua ini berjalan melalui labirin, kita dapat mengasumsikan bahwa solusinya jauh lebih sederhana. Sebenarnya, sebuah pilihan sederhana langsung memohon, tetapi saya benar-benar ingin membuat hal-hal yang indah .


Jika kita menempatkan artis kita di area terbuka dan memulai jalan-jalan acak, dia akan ragu di dekat posisi awalnya. Tetapi dengan diperkenalkannya dinding, bagian dari arah akan mulai memudar, derajat kebebasan akan menjadi kurang, dan dengan data input yang sama, agen akan bergerak lebih jauh.


Berikut ini adalah versi tim pengecekan kami untuk kesesuaian menyelamatkan robot dari labirin:


Kode
 M = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1 1 1 0 1 1 1 0 0 1 0 0 1 9 1 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0] mutable struct Point # point x::Int64 # vertical y::Int64 # horisont Point(x, y) = new(x, y) end function isexit(str, c) try for s in str if s == 'R' c.y+=M[cx, c.y+1]; elseif s == 'L' cy-=M[cx, cy-1]; elseif s == 'U' c.x+=M[c.x+1, cy]; elseif s == 'D' cx-=M[cx-1, cy]; else println("Error! Use only R, L, U, D") end end catch return true end return false end function test(Str) k = 0 n, m = 10,10 for i in 2:m+1, j in 2:n+1 if M[i,j] == 1 c = Point(i, j) a = isexit(S,c) if a k +=1 #println(a) end end end println(k, " test completed from ", sum(M)-9) end

Sekarang cukup menghasilkan garis acak hingga Anda mendapatkan satu yang berfungsi untuk semua posisi awal:


 using Random S = randstring("RLUD",200) "RDRRRDLRLUULURUDUUDLLLLLULLUDRRURDLDLULLRLUUUDURUUUULRUDUURUUDLRLLULRLUDRRLRRULLDULRRRRULRLLDULRLDRUDURDRUUDUUDDDDDLURRRRDRDURRRDDLLDUURRRLDRUDLRLLRDDRLRRRDDLLLRUURDRLURDLLUULLLLUURLLULUDULDDLDLLRLDUD" test(S) 41 test completed from 70

Selain itu, dimungkinkan untuk tidak repot dengan tes. Sudah cukup untuk membaca tugas dan menghasilkan string acak dengan kondisi maksimum yang diijinkan:


 for i in 1:20 S = randstring("RLUD",1000) test(S) end 70 test completed from 70 70 test completed from 70 70 test completed from 70 70 test completed from 70 55 test completed from 70# 65 test completed from 70# 70 test completed from 70 70 test completed from 70 38 test completed from 70# 70 test completed from 70 70 test completed from 70 56 test completed from 70# 70 test completed from 70 70 test completed from 70 70 test completed from 70 16 test completed from 70# 70 test completed from 70 24 test completed from 70# 70 test completed from 70 70 test completed from 70

Artinya, dengan probabilitas 70%, garis akan lulus tes.


Itu saja. Saya berharap pembaca sukses secara acak, sabar dan intuisi untuk solusi yang jelas.


Untuk yang penasaran - tautan untuk memperdalam topik:


Source: https://habr.com/ru/post/id451460/

More articles:


All Articles