Komentar ini didorong oleh penulisan artikel. Lebih tepatnya, satu frasa darinya.

... menghabiskan memori atau siklus prosesor pada item dalam miliaran dolar tidak baik ...

Kebetulan baru-baru ini saya harus melakukan hal itu. Dan, meskipun, kasus yang akan saya pertimbangkan dalam artikel ini agak istimewa - kesimpulan dan solusi yang diterapkan dapat bermanfaat bagi seseorang.

Sedikit konteks

Aplikasi iFunny menangani sejumlah besar konten grafis dan video, dan pencarian fuzzy untuk duplikat adalah salah satu tugas yang sangat penting. Ini sendiri merupakan topik besar yang pantas mendapatkan artikel terpisah, tetapi hari ini saya hanya akan berbicara sedikit tentang beberapa pendekatan untuk menghitung jumlah array yang sangat besar dalam kaitannya dengan pencarian ini. Tentu saja, setiap orang memiliki pemahaman yang berbeda tentang "array yang sangat besar", dan itu akan bodoh untuk bersaing dengan Hadron Collider, tetapi tetap saja. :)

Jika algoritma ini sangat singkat, maka untuk setiap gambar tanda tangan digitalnya (tanda tangan) dibuat dari 968 bilangan bulat, dan perbandingannya dibuat dengan menemukan "jarak" antara dua tanda tangan. Menimbang bahwa volume konten dalam dua bulan terakhir saja berjumlah sekitar 10 juta gambar, maka pembaca yang penuh perhatian akan dengan mudah mengetahuinya dalam benaknya - ini adalah persis "elemen dalam miliaran volume." Siapa yang peduli - selamat datang di kucing.

Pada awalnya akan ada cerita yang membosankan tentang menghemat waktu dan memori, dan pada akhirnya akan ada cerita instruktif singkat tentang fakta bahwa kadang-kadang sangat berguna untuk melihat sumbernya. Sebuah gambar untuk menarik perhatian secara langsung berkaitan dengan kisah instruktif ini.

Saya harus mengakui bahwa saya sedikit licik. Dalam analisis awal dari algoritma, dimungkinkan untuk mengurangi jumlah nilai di setiap tanda tangan dari 968 menjadi 420. Ini sudah dua kali lebih baik, tetapi urutan besarnya tetap sama.

Meskipun, jika Anda memikirkannya, saya tidak terlalu menipu, dan ini akan menjadi kesimpulan pertama: sebelum memulai tugas, ada baiknya berpikir - apakah mungkin untuk menyederhanakannya terlebih dahulu?

Algoritma perbandingannya cukup sederhana: akar dari jumlah kuadrat dari perbedaan dari dua tanda tangan dihitung, dibagi dengan jumlah nilai yang dihitung sebelumnya (mis., Dalam setiap iterasi penjumlahan akan tetap dan tidak dapat dianggap sebagai konstanta sama sekali) dan dibandingkan dengan nilai ambang. Perlu dicatat bahwa elemen tanda tangan terbatas pada nilai dari -2 hingga +2, dan, karenanya, nilai absolut dari selisih terbatas pada nilai dari 0 hingga 4.


Tidak ada yang rumit, tetapi kuantitas memutuskan.

Pendekatan pertama, naif

//  const val d = 0.3 // 10.000.000 . //      , //        val collection: MutableList<Signature> = mutableListOf() // signature —   420   Byte class Signature(val signature: Array<Byte>, val norma: Double) fun getSimilar(signature: Signature) = collection .filter { calculateDistance(it, signature) < d } fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> Math.pow((value - second.signature[index]).toDouble(), 2.0) }.sum()) / (first.norma + second.norma) 

Mari kita hitung apa yang kita miliki di sini dengan jumlah operasi:

10M Square Roots Math.sqrt
10M penambahan dan pembagian / (first.norma + second.norma)
4.200M pengurangan dan mengkuadratkan Math.pow((value - second.signature[index]).toDouble(), 2.0)
4.200M penambahan .sum()

Opsi apa yang kami miliki:

1. Dengan volume seperti itu, menghabiskan seluruh Byte (atau, Tuhan melarang, seseorang akan menduga untuk menggunakan Int ) untuk menyimpan tiga bit signifikan adalah pemborosan yang tidak termaafkan.
2. Mungkin, bagaimana cara mengurangi jumlah matematika?
3. Tetapi apakah mungkin untuk melakukan penyaringan awal, yang tidak begitu mahal secara komputasi?

Pendekatan kedua, kami kemas

Ngomong-ngomong, jika seseorang menyarankan bagaimana Anda dapat menyederhanakan perhitungan dengan kemasan seperti itu, Anda akan menerima banyak terima kasih dan plus dalam karma. Meski satu, tapi dengan sepenuh hati :)

One Long adalah 64 bit, yang, dalam kasus kami, akan memungkinkan kami untuk menyimpan 21 nilai di dalamnya (dan 1 bit akan tetap tidak tenang).

 //   20   Long class Signature(val signature: Array<Long>, val norma: Double) fun calculateDistance(first: Signature, second: Signature): Double = Math.sqrt(first.signature.mapIndexed { index, value -> calculatePartial(value, second.signature[index]) }.sum()) / (first.norma + second.norma) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L (0..60 step 3).onEach { val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7) sum += current * current } return sum.toDouble() } 

Lebih baik dari memori ( 4.200M versus 1.600M byte, jika kira-kira), tetapi bagaimana dengan perhitungannya?

Saya pikir sudah jelas bahwa jumlah operasi tetap sama dan 8.400M bergeser dan 8.400M logis telah ditambahkan ke mereka. Mungkin itu dapat dioptimalkan, tetapi trennya masih tidak bahagia - ini bukan yang kita inginkan.

Pendekatan ketiga, kemas ulang dengan sub-subs

Di pagi hari aku bisa mencium baunya, di sini kamu bisa menggunakan bit magic!

Mari kita simpan nilai bukan dalam tiga, tetapi dalam empat bit. Dengan cara ini:

Ya, kami akan kehilangan kepadatan kemasan dibandingkan dengan versi sebelumnya, tetapi kami akan mendapatkan kesempatan untuk menerima Long dengan 16 (tidak cukup) perbedaan dengan satu ohm satu XOR sekaligus. Selain itu, hanya akan ada 11 opsi untuk distribusi bit di setiap nibble akhir, yang akan memungkinkan Anda untuk menggunakan nilai pra-perhitungan dari kotak perbedaan.

 //   27   Long class Signature(val signature: Array<Long>, val norma: Double) // -1    val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16) fun calculatePartial(first: Long, second: Long): Double { var sum = 0L val difference = first xor second (0..60 step 4).onEach { sum += precomputed[(difference.ushr(it) and 0xF).toInt()] } return sum.toDouble() } 

Dari memori menjadi 2.160M dibandingkan 1.600M - tidak menyenangkan, tetapi masih lebih baik dari 4.200M awal.

Mari kita hitung operasi:

Akar, penambahan, dan divisi 10M kuadrat (tidak kemana-mana)
270M XOR
4.320 penambahan, pergeseran, 4.320 logis, dan ekstrak dari array.

Itu sudah terlihat lebih menarik, tetapi, bagaimanapun, ada terlalu banyak perhitungan. Sayangnya, tampaknya kami telah menghabiskan 20% dari upaya memberikan 80% dari hasilnya dan sekarang saatnya untuk memikirkan di mana lagi Anda bisa mendapat untung. Hal pertama yang terlintas dalam pikiran adalah tidak membawanya ke perhitungan sama sekali, menyaring tanda tangan jelas tidak pantas dengan beberapa filter ringan.

Pendekatan keempat, ayakan besar

Jika Anda sedikit mengubah rumus perhitungan, Anda bisa mendapatkan ketimpangan ini (semakin kecil jarak yang dihitung, semakin baik):


Yaitu sekarang kita perlu mencari cara bagaimana menghitung nilai minimum yang mungkin dari sisi kiri ketidaksetaraan berdasarkan informasi yang kita miliki pada jumlah bit yang ditentukan dalam Long 's. Maka cukup buang semua tanda tangan yang tidak memuaskannya.
Biarkan saya mengingatkan Anda bahwa x _saya dapat mengambil nilai dari 0 hingga 4 (tandanya tidak penting, saya pikir itu jelas mengapa). Mengingat bahwa setiap istilah dikuadratkan, mudah untuk mendapatkan pola umum:


Formula terakhirnya terlihat seperti ini (kami tidak akan membutuhkannya, tapi saya menyimpulkannya untuk waktu yang lama dan akan memalukan untuk melupakan dan tidak menunjukkan kepada siapa pun):


Di mana B adalah jumlah bit yang ditetapkan.

Bahkan, dalam satu Long hanya 64 bit, baca 64 hasil yang mungkin. Dan mereka dengan sempurna dihitung sebelumnya dan ditambahkan ke array, dengan analogi dengan bagian sebelumnya.

Selain itu, itu sepenuhnya opsional untuk menghitung semua 27 Panjang - itu sudah cukup untuk melampaui ambang batas pada yang berikutnya dan Anda dapat mengganggu cek dan mengembalikan false. Pendekatan yang sama, omong-omong, dapat digunakan dalam perhitungan utama.

 fun getSimilar(signature: Signature) = collection .asSequence() //     !? .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256) fun estimate(first: Signature, second: Signature):Boolean{ var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong() first.signature.forEachIndexed { index, value -> bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])] if (bitThreshold <= 0) return false } return true } 

Di sini harus dipahami bahwa efektivitas filter ini (hingga negatif) sangat tergantung pada ambang yang dipilih dan, sedikit kurang kuat, pada data input. Untungnya, untuk ambang yang diperlukan d=0.3 sejumlah kecil objek berhasil melewati filter dan kontribusi perhitungannya terhadap total waktu respons sangat sedikit sehingga mereka dapat diabaikan. Dan jika demikian, maka Anda dapat menghemat sedikit lebih banyak.

Pendekatan kelima, menyingkirkan urutan

Ketika bekerja dengan koleksi besar, sequence adalah pertahanan yang baik terhadap kehabisan memori yang sangat tidak menyenangkan. Namun, jika kita jelas tahu bahwa pada filter pertama koleksi akan dikurangi menjadi ukuran yang waras, maka pilihan yang jauh lebih masuk akal adalah menggunakan iterasi biasa dalam satu lingkaran dengan penciptaan koleksi perantara, karena sequence tidak hanya modis dan awet muda, tetapi juga sebuah iterator, yang memiliki sahabat berikutnya yang jauh dari bebas.

 fun getSimilar(signature: Signature) = collection .filter { estimate(it, signature) } .filter { calculateDistance(it, signature) < d } 

Tampaknya ini adalah kebahagiaan, tetapi saya ingin "menjadikannya indah." Di sini kita sampai pada kisah instruktif yang dijanjikan.

Pendekatan keenam, kami menginginkan yang terbaik

Kami menulis di Kotlin, dan di sini beberapa java.lang.Long.bitCount asing! Dan baru-baru ini, tipe yang tidak ditandatangani dimasukkan ke dalam bahasa. Serang!

Tidak lebih cepat dikatakan daripada dilakukan. Semua ULong digantikan oleh ULong , ULong dari sumber Java dan ditulis ulang sebagai fungsi ekstensi untuk ULong

 fun ULong.bitCount(): Int { var i = this i = i - (i.shr(1) and 0x5555555555555555uL) i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL) i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL i = i + i.shr(8) i = i + i.shr(16) i = i + i.shr(32) return i.toInt() and 0x7f } 

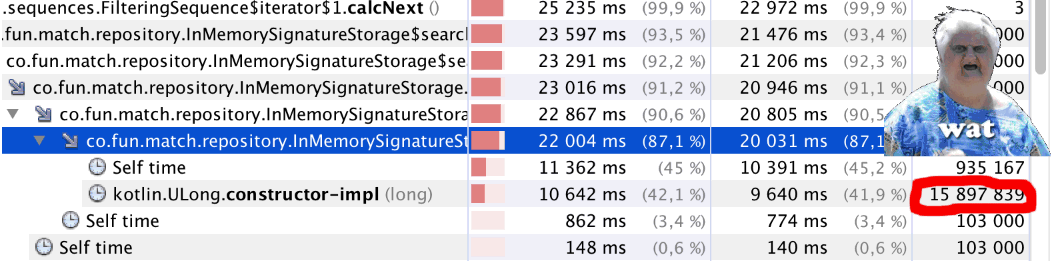
Kita mulai dan ... Ada yang salah. Kode mulai bekerja lebih lambat. Kami memulai profiler dan melihat sesuatu yang aneh (lihat bitCount() artikel): sedikit kurang dari satu juta panggilan ke bitCount() hampir 16 juta panggilan ke Kotlin.ULong.constructor-impl . WAT!?

Teka-teki itu dijelaskan secara sederhana - lihat saja kode kelas ULong

 public inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable<ULong> { @kotlin.internal.InlineOnly public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data)) @kotlin.internal.InlineOnly public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data)) @kotlin.internal.InlineOnly public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount) @kotlin.internal.InlineOnly public inline operator fun inc(): ULong = ULong(data.inc())  .. } 

Tidak, saya mengerti segalanya, ULong masih experimental sekarang, tapi bagaimana itu !?
Secara umum, kami mengakui pendekatan itu gagal, yang sangat disayangkan.

Yah, tapi tetap saja, mungkin sesuatu yang lain bisa diperbaiki?

Sebenarnya kamu bisa. Kode java.lang.Long.bitCount asli bukan yang paling optimal. Ini memberikan hasil yang baik dalam kasus umum, tetapi jika kita tahu sebelumnya tentang prosesor mana aplikasi kita akan bekerja, maka kita dapat memilih cara yang lebih optimal - di sini adalah artikel yang sangat baik tentang hal itu di Habré. Saya sangat merekomendasikan menghitung bit tunggal , saya sangat merekomendasikan membacanya.

Saya menggunakan "Metode Gabungan"

 fun Long.bitCount(): Int { var n = this n -= (n.shr(1)) and 0x5555555555555555L n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L) n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56) return n.toInt() and 0x7F } 

Menghitung burung beo

Semua pengukuran dilakukan secara acak, selama pengembangan pada mesin lokal dan direproduksi dari memori, sehingga sulit untuk berbicara tentang akurasi, tetapi Anda dapat memperkirakan perkiraan kontribusi masing-masing pendekatan.

Kesimpulan

• Ketika berhadapan dengan pemrosesan data dalam jumlah besar, perlu menghabiskan waktu untuk analisis pendahuluan. Mungkin tidak semua data ini perlu diproses.
• Jika Anda dapat menggunakan pra-penyaringan yang kasar, tetapi murah, ini dapat banyak membantu.
• Sihir bit adalah segalanya bagi kami. Nah, jika ada, tentu saja.
• Untuk melihat kode sumber dari kelas dan fungsi standar terkadang sangat berguna.

Terima kasih atas perhatian anda! :)

Dan ya, untuk dilanjutkan.