Untuk mengirimkan pesan dari stasiun pangkalan ke perangkat seluler (dan sebaliknya), gelombang elektromagnetik harus mengatasi sejumlah kendala: refleksi, refraksi, hamburan, bayangan, pergeseran frekuensi Doppler, dan sebagainya. Pertama, semua efek ini disebut multiplicative (dari bahasa Inggris. Multiplication - multiplication) - sesuai dengan model matematika dari efek tersebut. Dan, kedua, dapat dikumpulkan dengan istilah umum fading .

Dari standar ke standar, dari generasi ke generasi, dari teknologi ke teknologi, para ilmuwan dan insinyur telah berjuang dan berjuang dengan masalah leveling ini memudar (mitigasi memudar).

Dan beberapa solusi tersebar luas. Katakan lebih banyak: hampir semuanya, satu atau lain cara, dikaitkan dengan konsep keanekaragaman .

Sumber ilustrasi (tidak, ini bukan iklan, hanya kombinasi sukses dari istilah dan kucing yang diinginkan).

Contoh dari solusi tersebut:

Frekuensi hopping - terhadap frekuensi selektif memudar;
Estimasi dan penyamaan saluran melalui umpan balik - GSM, untuk menekan perubahan dalam domain waktu;
Ekstensi Spectrum (UMTS);
Sinyal pilot (dimulai dengan UMTS) pada downlink (Down-link) dan pelacakan sinyal (signal tracking) pada uplink (Up-link) - untuk menekan perubahan dalam domain waktu;
OFDM - LTE, terhadap fading selektif frekuensi;
Keragaman temporal ( pengkodean koreksi kesalahan );
Keragaman polarisasi (di sisi pemancar) + Adders (kombinator, di sisi penerima);
Keragaman spasial .

Yang terakhir dari teknik ini akan kita pertimbangkan hari ini sebagai bagian dari topik lain di MIMO .

Urutan keragaman ruang dan penguatan larik

Yang pertama.

Ada konsep seperti itu - urutan keragaman ruang: jika informasi yang sama dapat dikumpulkan dari arah yang berbeda , maka harapan untuk memulihkannya akan meningkat dengan benar. Sebagai contoh dari kehidupan, kita dapat membayangkan mengumpulkan informasi tentang peristiwa yang sama dari sumber informan independen. Dalam komunikasi radio, kami dapat meningkatkan pesanan ini, termasuk dengan menggunakan MISO , SIMO atau MIMO .

Batas teoretis keanekaragaman seperti itu M_TM_R dimana M_T - jumlah antena pemancar, dan M_R - jumlah antena penerima. Ingat ini.

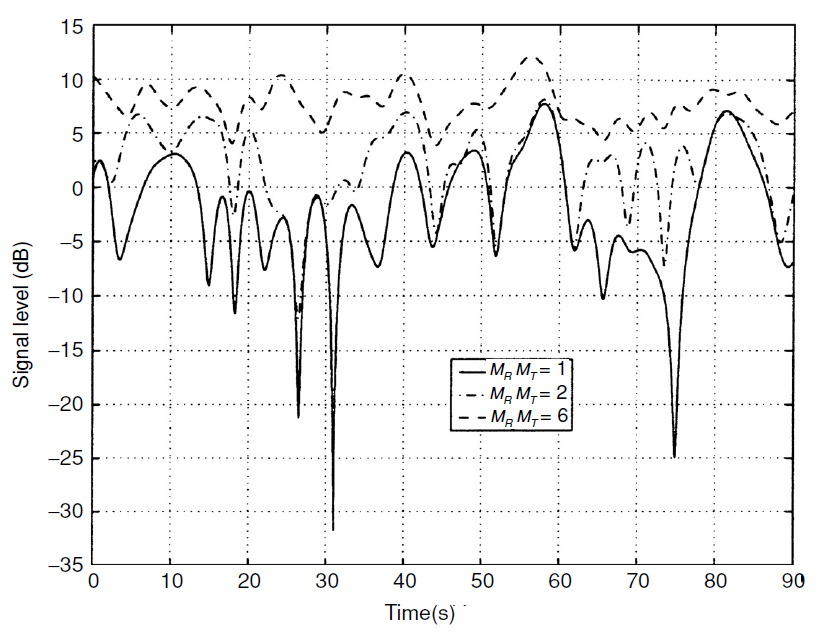
Fig. 1. Stabilitas saluran disebabkan oleh peningkatan tatanan keragaman spasial. Pada nilai $M_TM_R \ hingga \ infty$ saluran sepenuhnya distabilkan dan akan berubah menjadi saluran tanpa fading (AWGN) [1, hlm . 101] .

Yang kedua.

Dengan menggunakan SIMO , MIMO, dan bahkan MISO (dalam hal saluran yang terkenal), orang dapat memperoleh apa yang disebut gain array . Ini berarti bahwa penggunaan beberapa antena penerima dan / atau distribusi energi yang tepat pada sisi transmisi dapat meningkatkan rasio signal-to-noise (SNR) - dan dengan demikian mengurangi jumlah kesalahan.

Urutan keragaman dan penguatan array untuk berbagai konfigurasi dapat diturunkan secara analitis [1, hal. 86 - 100] dan kurangi menjadi satu tabel [1, hlm. 101] baik untuk kasus ketika saluran tidak diketahui (CU - Channel Unknown) dan untuk kasus ketika saluran diketahui (CK - Channel Unown) di sisi pemancar.

Konfigurasi	Urutan keanekaragaman	Keuntungan array
SIMO (CU, Rx-MRC)
SIMO (CK, Rx-MRC)
MISO (CU, OSTBC)		1
MISO (CK, Tx-MRC)
MIMO (CU, OSTBC)
MIMO (CK, DET)

Oke, bahkan dengan pukulan lebar, tapi sekarang kita memiliki setidaknya beberapa pemahaman tentang aspek teoritis dari penekanan fading. Pertanyaan selanjutnya adalah bagaimana cara mencapai batas teoritis ini? Apa teknik untuk mengaktifkan kemenangan yang dianggap?

Solusi No. 1. Kode ruang waktu

Salah satu kelas solusi yang paling populer untuk keragaman spasial adalah, mungkin, kelas kode ruang-waktu (kode ruang-waktu). Sebagai contoh, yang saya kenal, banyak metode Alamouti (contoh kode blok) [2, hlm. 40-46]:

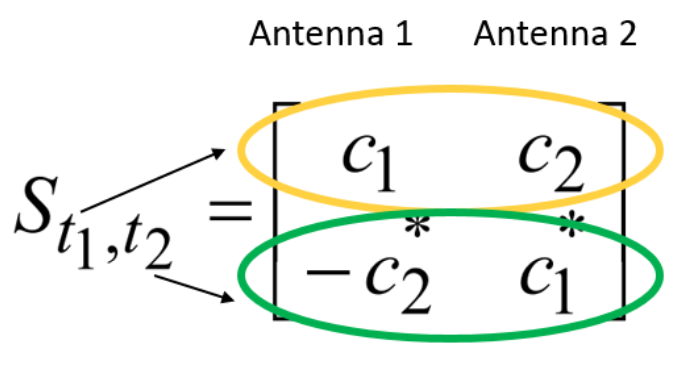
dimana c_i di i = 1,2 Apakah beberapa karakter input t_i di i = 1,2 Apakah slot waktu, dan $\ mathbf {S}$ - ini, sebenarnya, adalah matriks pengkodean.

Skema Alamouti bersifat ortogonal [1, hlm. 93-95, 97-98] dan, yang paling penting, tidak memerlukan Informasi Saluran Negara.

Deskripsi matematis dari transmisi sinyal yang dikodekan oleh skema Alamouti, serta beberapa contoh pemodelan teknik ini di MatLab dapat ditemukan di repositori saya . Tertarik dengan sambutan!

Namun, seperti yang Anda lihat, sirkuit Alamouti adalah kasus di mana kami hanya memiliki dua antena pemancar ( M_T = 2 )
Tapi jangan berkecil hati sebelumnya: tentu saja, opsi lain tersedia, mereka hanya disebut sedikit berbeda. Misalnya, menurut [3], seseorang dapat menerapkan skema pengkodean berikut:

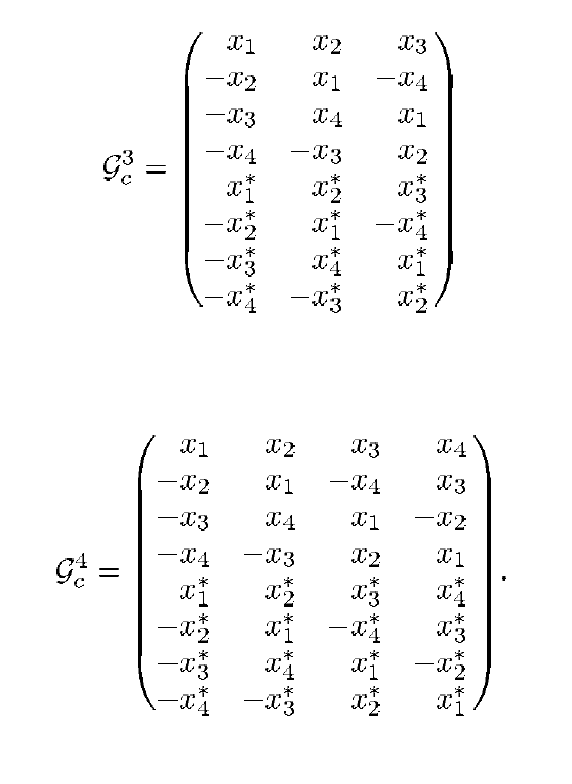
Fig. 2. Skema transfer untuk kasus dan [2].

Dan ada banyak pilihan lain: hanya untuk memenuhi kondisi orthogonality.

Kode semacam itu membutuhkan, pada kenyataannya, prosedur yang sama untuk encoding dan decoding seperti untuk kode Alamouti. Oleh karena itu, mereka biasanya digabungkan dengan istilah umum kode blok ruang-waktu ortogonal (OSTBC - Kode Blok Ruang-Waktu Ortogonal).

Banyak perhatian diberikan pada kelas kode ini dalam materi "Pengantar Sistem MIMO" dari MathWorks. Saya sangat menyarankan semua orang tertarik untuk membacanya!

Berapa harganya?

Seperti dapat dilihat dari skema transmisi, meskipun kami mengirimkan simbol secara paralel, kami menghabiskan beberapa slot waktu untuk hal ini. Oleh karena itu, kami mengorbankan bandwidth (setidaknya, kami mendapatkannya lebih sedikit). Untuk skema Alamouti, kompromi seperti itu simetris: kami menggunakan 2 antena dan 2 slot waktu (seolah-olah menggunakan SISO dalam hal bandwidth). Skema lain mungkin lebih memengaruhi kecepatan transmisi.

Keputusan nomor 2. DET: Transmisi Eigenmode Dominan

Nah, untuk kelas teknik sebelumnya, pengetahuan tentang saluran itu tidak penting bagi kami. Tetapi bagaimana jika kita masih memiliki pengetahuan ini? Apakah ada teknik yang lebih cocok dalam kasus ini?

Dalam salah satu artikel saya sebelumnya, kami membahas bahwa, setelah mengetahui kondisi saluran, kami dapat menerapkan berbagai metode pemrosesan sinyal untuk meningkatkan throughput. Prinsip yang sama berfungsi untuk meningkatkan kekebalan kebisingan.

Mungkin, banyak yang telah mendengar tentang metode MRC dan banyak yang tahu bahwa metode ini sangat cocok untuk kasus SIMO , ketika ada setidaknya satu antena pada transmisi, tetapi masih ada banyak dari mereka, yang berarti ada sesuatu untuk digabungkan.

Tapi, mungkin, sudah lebih sedikit jumlah pembaca yang menemukan MRC di sisi transmisi (Tx-MRC) [1, hal. 95,96], dan bahkan lebih sedikit lagi dengan teknologi DET (Dominant Eigenmode Transmission) [1, hlm. 98-100]. Perbaiki!

Untuk memulai, pertimbangkan kasus umum saluran MIMO dan yang terakhir dari metode ini - DET.

Apa inti dari:

Jika pemancar memiliki matriks $\ mathbf {H}$ maka bisa diproses.
Misalnya, dekomposisikan melalui SVD : $\ mathbf {H} = \ mathbf {U} \ mathbf {\ Sigma} \ mathbf {V} ^ H$ dengan demikian memperoleh beberapa matriks dari properti tertentu.
Properti ini dapat digunakan untuk mengoptimalkan transfer, misalnya, menggunakan pra-coding (pra-coding).

Kami memperkenalkan beberapa vektor pra-pengkodean:

$\ underset {M_T \ times1} {\ mathbf {w}} = \ sqrt {M_T} \ underset {M_T \ times1} {\ mathbf {v} _1}$

dimana $\ mathbf {v} _1$ Merupakan vektor matriks pertama (dominan, bisa dikatakan) $\ mathbf {V}$ .

Selain itu, kami juga dapat menulis vektor pasca pemrosesan:

$\ underset {M_R \ times1} {\ mathbf {g}} = \ underset {M_R \ times1} {\ mathbf {u} _1}$

dimana $\ mathbf {u} _1$ Merupakan vektor pertama dari matriks $\ mathbf {U}$ .

Definisikan kembali model sinyal yang diterima (lihat topik bandwidth ):

${z} = \ underset {1 \ kali M_R} {\ mathbf {g} ^ H} \ underset {M_R \ kali 1} {\ mathbf {y}} = \ mathbf {g} ^ H \ sqrt {\ frac { E_s} {M_T}} \ mathbf {H} \ mathbf {w} s + \ mathbf {g} ^ H \ mathbf {n} = \ sqrt {E_s} \ mathbf {u} _1 ^ H \ mathbf {H} \ mathbf {v} _1 s + \ hat {\ mathbf {n}} = \ sqrt {E_s} \ sigma_ {max} s + \ hat {\ mathbf {n}}$

Voila! Keajaiban aljabar linier dipilih di antara semua jalur distribusi yang paling menguntungkan dan mengarahkan semua energi di sana. Sebenarnya, kita memiliki algoritma linear beamforming sebelum kita.

Dengan biaya pendekatan ini, seperti halnya dalam kasus OSTBC, batasan bandwidth adalah. Benar, ini sekarang terjadi murni dalam domain spasial.

Mengapa metode ini mengandung nilai eigen dalam namanya jika kita hanya berbicara tentang yang tunggal?

Karena nilai eigen (kardinalitas jalur propagasi - fading) dapat langsung diturunkan dari bilangan tunggal (amplitudo fading):

$\ mathbf {R} _ {\ mathbf {HH} ^ H} = \ mathbf {HH} ^ H = \ mathbf {Q} \ mathbf {\ Lambda} \ mathbf {Q} ^ H = \ mathbf {Q} \ begin {bmatrix} \ lambda_ {max} & & & & \\ &. & & & \\ & &. & & \\ & & &. & \\ & & & & lambda_ {min} \\ \ end {bmatrix} \ mathbf {Q} ^ H$

Nah, dengan DET kurang lebih jelas apa dengan Tx-MRC?

Lebih mudah dengannya - ini adalah kasus khusus DET, dan sekarang kami akan membuktikannya.

Untuk Tx-MRC, vektor pra-pengkode berikut ini diusulkan dalam literatur:

$\ mathbf {w} = \ sqrt {M_T} \ frac {\ mathbf {h} ^ H} {\ sqrt {|| \ mathbf {h} || ^ 2_F}}$

Kami ingat bahwa kuadrat dari norma Frobenius sama dengan nilai eigen dan, karenanya, kuadrat dari bilangan tunggal $|| \ mathbf {h} || ^ 2_F = \ lambda_ {max} = \ sigma ^ 2_ {max}$ (dalam hal SIMO dan MISO).

Kemudian kami mendefinisikan kembali model sinyal yang diterima, hanya untuk kasus MISO:

$y = \ sqrt {\ frac {E_s} {M_T}} \ mathbf {h} \ mathbf {w} s + \ mathbf {n} = \ sqrt {\ frac {E_s} {M_T}} \ mathbf {h} \ sqrt {M_T} \ frac {\ mathbf {h} ^ H} {\ sqrt {|| \ mathbf {h} || ^ 2_F}} s + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} \ mathbf {h} \ mathbf {h} ^ Hs + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} || \ mathbf {h } || _F ^ 2 s + \ mathbf {n}} = \ frac {\ sqrt {E_s}} {\ sigma_ {max}} \ lambda_ {max} s + \ mathbf {n}} = \ sqrt {E_s} \ sigma_ {maks} s + \ mathbf {n}}$

Yang harus dibuktikan.

Perhatikan, sekarang kita berbicara tidak hanya tentang pemisahan sinyal di sisi transmisi dan menggabungkannya di sisi penerima, seperti halnya dengan OSTBC. Sekarang kita berbicara tentang distribusi energi yang optimal. Ini berarti bahwa nilai-nilai gain array dalam kasus ini lebih tinggi daripada OSTBC.

Sekarang semua kata telah diucapkan, kami akan mencoba untuk mensimulasikan teknik kami.

Pemodelan

Hari ini saya menghitung sedikit: untuk pemodelan OSTBC , objek siap pakai dari Communication Toolbox digunakan (MatLab R2014a - yang mana itu):

comm.OSTBCEncoder - Ortogonal Space-Time Block Codes Encoder;
comm.OSTBCCombiner - Ortogonal Space-Time Block Codes Combiner.

Untuk modulasi dan demodulasi (dan perhitungan kesalahan bit - BER), fungsi tidak lagi digunakan, tetapi fungsi . Analoginya ada dalam paket Octave komunikasi .

Kode sumber dapat ditemukan di sini.

clear all; close all; clc snapshots = 100000; EbNo = 0:15; M = 2; % modulation order (BPSK) Mt = 2; % num. of Tx antennas Mr = [1; 2]; % num. of Rx antennas ostbcEnc = comm.OSTBCEncoder('NumTransmitAntennas', Mt); % for Alamouti ric_ber = zeros(length(EbNo), length(M), length(Mr)); sum_BER_alam = zeros(length(EbNo), length(M), length(Mr)); sum_BER_det = zeros(length(EbNo), length(M), length(Mr)); for mr = 1:length(Mr) ostbcComb = comm.OSTBCCombiner('NumTransmitAntennas', Mt, 'NumReceiveAntennas', Mr(mr)); H = zeros(Mr(mr), Mt, snapshots); alam_fad_msg = zeros(snapshots, Mr(mr)); for m = 1:length(M) ric_ber(:,m,mr) = berfading(EbNo, 'psk', M(m), Mr(mr)*Mt, 0); snr = EbNo+10*log10(log2(M(m))); % Signal-to-Noise Ratio message = randi([0, M(m)-1],100000,1); mod_msg = pskmod(message, M(m), 0, 'gray'); Es = mean(abs(mod_msg).^2); % symbol energy alam_msg = step(ostbcEnc, mod_msg); % OSTBC encoding % Channel h = (1/sqrt(2))*(randn(Mr(mr),Mt,snapshots/Mt)... + 1j*randn(Mr(mr),Mt, snapshots/Mt)); % Rayleigh flat fading % Channel is stable during to time-slots: H(:,:,1:2:end-1) = h; H(:,:,2:2:end) = h; pathGainself = permute(H,[3,2,1]); % Transmit through the channel (Alamouti): for q = 1:snapshots; alam_fad_msg(q,:) = (sqrt(Es/Mt)*H(:,:,q)*alam_msg(q,:).').'; end % DET: sigmas = zeros(length(mod_msg), 1); for hi = 1:length(mod_msg) [U, Sigma, Vh] = svd(H(:, :, hi)); sigmas(hi) = Sigma(1, 1); end det_fad_msg = mod_msg.*sigmas; No = Es./((10.^(EbNo./10))*log2(M(m))); % Noise spectrum density for c = 1:500 for jj = 1:length(EbNo) alam_noisy_msg = alam_fad_msg + ... sqrt(No(jj)/2)*(randn(size(alam_fad_msg)) + ... 1j*randn(size(alam_fad_msg))); % AWGN alam_decodeData = step(ostbcComb,alam_noisy_msg,pathGainself); %OSTBC combining alam_demod_msg = pskdemod(alam_decodeData, M(m), 0, 'gray'); % demodulation [number,alam_BER(c,jj)] = biterr(message, alam_demod_msg); % BER det_noisy_msg = det_fad_msg+ ... sqrt(No(jj)/2)*(randn(size(mod_msg)) + ... 1j*randn(size(mod_msg))); %AWGN det_decodeData = det_noisy_msg./sigmas; % Zero-Forcing equalization det_demod_msg = pskdemod(det_decodeData, M(m), 0, 'gray'); % demodulation [number,det_BER(c,jj)] = biterr(message, det_demod_msg); % BER end end sum_BER_alam(:,m, mr) = sum(alam_BER)./c; sum_BER_det(:,m, mr) = sum(det_BER)./c; end end figure(1) semilogy(EbNo, sum_BER_alam(:, 1, 1), 'b-o', ... EbNo, sum_BER_det(:,1,1), 'b->',... EbNo, ric_ber(:,1,1), 'b-',... EbNo, sum_BER_alam(:, 1, 2), 'r-o', ... EbNo, sum_BER_det(:,1,2), 'r->',... EbNo, ric_ber(:,1,2), 'r-',... 'LineWidth', 1.5) title('BPSK (Rayleigh flat fading)') legend('Alamouti (2x1)','Tx-MRC (2x1)','2-nd order diversity', ... 'Alamouti (2x2)','DET (2x2)','4-th order diversity') xlabel('EbNo (dB)') ylabel('BER') grid on

Seharusnya menghasilkan sesuatu seperti ini:

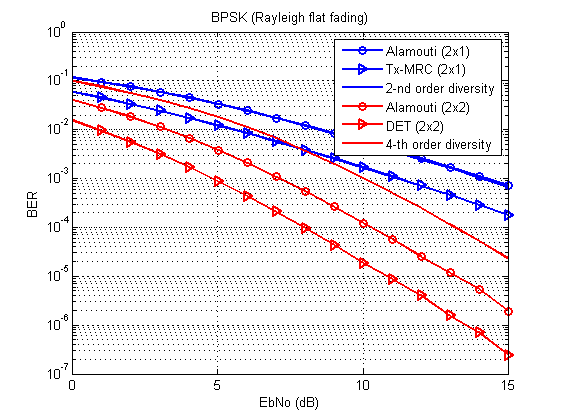
Fig. 3. Kurva kesalahan bit / simbol untuk teknik transmisi yang berbeda (BPSK, saluran Rayleigh dengan flat fading). Bandingkan dengan [1, hlm. 96, 100].

Dan sekarang pertanyaannya adalah: di mana kurva batas teoretis keanekaragaman urutan kedua?

Jawabannya

Semuanya sesuai dengan tabel: kurva ini sepenuhnya bertepatan dengan Alamouti 2x1. Dalam kasus MIMO, penguatan array juga ikut berperan, sehingga kurva dipisahkan.

Dengan satu atau lain cara, dan DET (atau Tx-MRC) diharapkan untuk mengungguli Alamouti dalam kualitas.

Seperti ini: pengetahuan adalah kekuatan!

Sastra

Paulraj, Arogyaswami, Rohit Nabar, dan Dhananjay Gore. Pengantar komunikasi nirkabel ruang-waktu. Cambridge University Press, 2003.
Bakulin M. G., Varukina L. A., Kreindelin V. B. Teknologi MIMO: prinsip-prinsip dan algoritme // M.: Hot line - Telecom. - 2014 .-- T. 244.
Tarokh, V., Jafarkhani, H., & Calderbank, AR (1999). Kode blok ruang-waktu dari desain ortogonal. Transaksi IEEE pada teori Informasi, 45 (5), 1456-1467.

Kepada staf pengajar dan persaudaraan mahasiswa dari profesi asli saya, saya menyapa!

Keragaman spasial MIMO: Alamouti, DET, dan keragaman spasial lainnya

Urutan keragaman ruang dan penguatan larik

Solusi No. 1. Kode ruang waktu

Keputusan nomor 2. DET: Transmisi Eigenmode Dominan

Pemodelan

Sastra

More articles: