Diketahui bahwa sebagian besar rangkaian waktu yang harus dihadapi oleh peneliti adalah tidak stasioner, dan analisisnya secara signifikan lebih rumit daripada studi tentang proses stasioner. Karena minat terhadap gelombang tampaknya telah mereda, maka akan bermanfaat untuk membahas beberapa instrumen "non-stasioner" lainnya yang berguna terutama untuk memperkirakan frekuensi sesaat, serta untuk mengevaluasi spektrum sesaat.
Pertama-tama, masuk akal untuk mengingat "sinyal analitik". Di bawah, "An-model" mengacu pada impedansi dan kekuatan sesaat dari sinyal uji setelah selesainya bagian imajinernya (digeser dalam fase dengan π / 2).
Tetapi tidak selalu mungkin untuk mengotak-atik transformasi Gilbert. Sebelumnya, metode estimasi spektral autoregresif yang cocok untuk bekerja dengan sekuens pendek telah
disebutkan . Di sini, "AR-model" akan dipahami sebagai studi fragmen pendek (dari 5 sampel) yang tumpang tindih dari sinyal asli untuk menentukan koefisien autoregresi orde dua, menemukan "kutub" model dari mereka, dll.

Kedua metode yang dijelaskan di sini didasarkan pada satu prinsip - asumsi bahwa dalam lingkungan kecil dari momen waktu yang dipilih proses yang diteliti dapat didekati dengan urutan "eksponensial" - satu kompleks (An) atau jumlah dari dua eksponensial konjugat kompleks (AR).
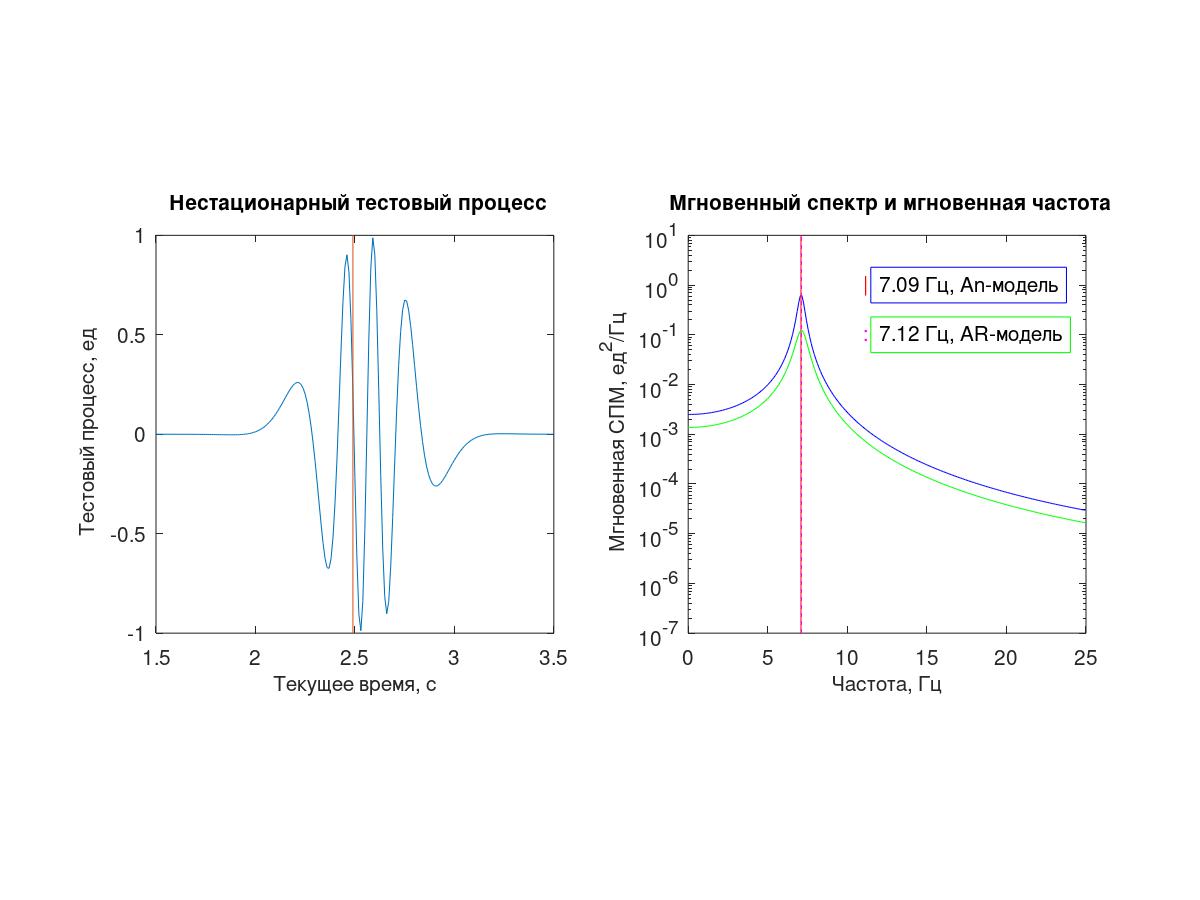
Sebagai proses pengujian, urutan 512 sampel dengan interval pengambilan sampel bersyarat Δt = 0,01 diperoleh dari proses deterministik kontinu (1) digunakan.
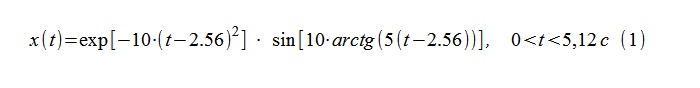
Dengan "logaritma" dan diferensiasi selanjutnya dari pengisian frekuensi tinggi dan amplop, masing-masing, dari (1), ekspresi teoritis untuk frekuensi (sesaat) dan pengurangan (2) diperoleh

Untuk pemodelan-An dengan metode periodogram (transformasi Fourier langsung dan terbalik), sinyal analitik y [i] dihasilkan dari urutan awal x [i].
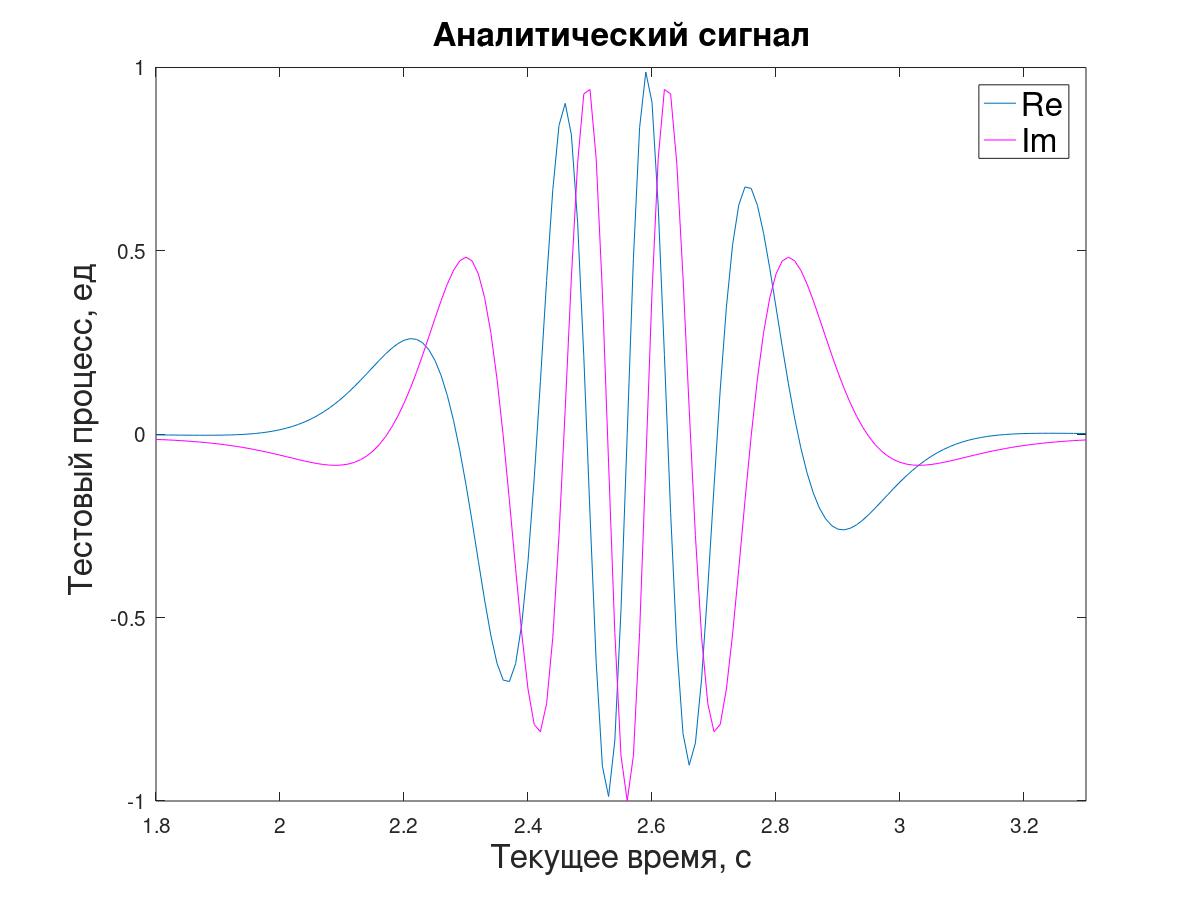
Rasio dua sampel berturut-turut dari sinyal seperti itu, pada prinsipnya, memungkinkan Anda untuk menentukan impedansi instan λ, tetapi untuk menyederhanakan tugas demonstrasi ini - agar tidak repot dengan membuat sampel perantara atau menjelaskan pergeseran estimasi dengan Δt / 2 - diputuskan untuk bekerja dengan sampel "melalui satu", menghitung λ
i sehubungan dengan nilai sinyal y [i + 1] berikutnya ke y [i-1] sebelumnya (3).

Untuk pemodelan AR (model orde kedua), prosedur standar untuk menghitung koefisien autokorelasi 1, a
1i , a
2i menggunakan persamaan Yule-Walker digunakan, dan urutan 5 sampel x [i-2], x [i -1], ... x [i + 2] (4).
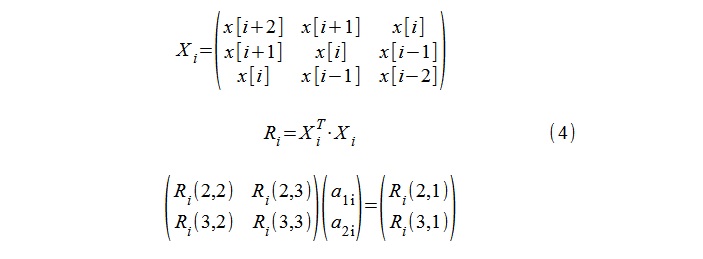
"Kutub" model λ
i kemudian dengan mudah dihitung dengan logaritma akar persamaan kuadratik (5).
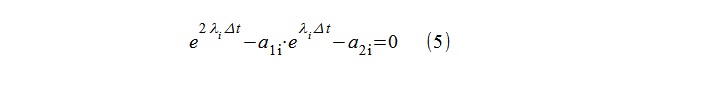

Konstruksi estimasi spektral dari "kutub" yang diketahui hingga faktor skala
tidak sulit . Selanjutnya "Kekuatan sesaat" untuk model-An jelas didefinisikan sebagai | y [i] |
2 , dan pertanyaan tentang penskalaan perkiraan ini tampaknya diselesaikan. Untuk model AR, teknik biasa yang terkait dengan menentukan kekuatan white noise konvensional, dalam kasus sinyal tidak stabil, "tidak bekerja". Karena kurangnya ide terbaik, penskalaan diterapkan berdasarkan rata-rata kuadrat dari 5 sampel yang sesuai. Tampaknya tidak ada lagi yang bisa dilakukan dengan menganalisis hanya urutan 5 sampel. Animasi ini menunjukkan bagaimana grafik AR-SPM terkadang terlihat “gagal” relatif terhadap skor-An. Harus dipahami bahwa momen-momen transisi “hingga nol” untuk model AR bisa menjadi sulit tidak hanya dalam hal kesalahan dengan frekuensi sesaat, tetapi juga dengan amplitudo seketika, terutama di wilayah frekuensi rendah.
Beberapa komentar pada akhirnya.
- Dari pengalaman, kedua metode biasanya memberikan hasil yang baik untuk memperkirakan frekuensi sesaat, setidaknya dalam rentang frekuensi rata-rata (berdasarkan frekuensi sampling).
- Kualitas relatif tinggi dari hasil metode-An, kesederhanaan dan kemudahan pemahaman dan implementasi lebih dari "dikompensasi" oleh kemungkinan kesulitan dengan mengubah proses menurut Gilbert. Filter digital Gilbert dengan kualitas baik, terutama dalam rentang frekuensi yang luas, dapat memiliki urutan yang sangat tinggi. Ketika menerapkan metode periodogram alternatif dari transformasi ini, harus diperhitungkan bahwa transformasi Fourier secara implisit menyiratkan penyelesaian proses menjadi periodik. Akibatnya, penyelesaian signifikan yang signifikan dari proses dengan nol mungkin diperlukan. Kualitas tinggi dari hasil An-metode dijelaskan oleh penggunaan informasi pada lingkungan yang sangat luas dari instan waktu yang dipilih (secara tegas - pada seluruh implementasi sementara dari proses), dan properti yang sama ini membuatnya sulit untuk menerapkan metode (misalnya, ketika bekerja dalam waktu nyata).
- Jika perlu, langkah-langkah berikut dapat direkomendasikan untuk meningkatkan hasil metode AR:
- Penipisan data (pada tingkat pengambilan sampel yang sangat tinggi)
- Peningkatan jumlah rata-rata - perluasan "momen waktu" yang terlibat dalam lingkungan model - pembangunan matriks trek X dengan sejumlah besar baris.
- Meningkatkan urutan model AR.