Dalam ilmu asinkron, tempat utama ditempati oleh properti sirkuit, yang disebut kemerdekaan bebas, dalam bahasa Inggris kecepatan independen (selanjutnya SI). Dipercayai bahwa properti ini adalah analog dari independensi sirkuit asinkron dari penundaan elemen-elemen logika. Tidak mengherankan, istilah SI disebutkan di hampir setiap pekerjaan di asynchrony. Namun secara berkala beberapa keraguan samar muncul mengenai istilah ini. Bukan kebetulan bahwa istilah ini semakin digantikan oleh istilah lain yang disebut sinkronisasi diri. Seruan kepada sumber akan membantu memperjelas situasi ini. Kita berbicara tentang
volume kedua dari buku R. Miller Teori tentang Switching Circuits, atau lebih tepatnya, Bab 10, disebut Theory of Switching Circuits, Independen dari Kecepatan.
Jadi, inilah definisi sirkuit independen kecepatan.

Kelas (ekivalen) adalah satu set lengkap keadaan yang dapat diterima dari suatu rangkaian sedemikian rupa sehingga untuk setiap keadaan dari himpunan ini terdapat urutan keadaan yang dapat diterima dimulai dari keadaan tertentu dan berisi semua keadaan dari himpunan yang diberikan. Dengan kata lain, dari keadaan kelas mana pun Anda bisa masuk ke kelas mana pun dari kelas yang sama.
Kelas (ekuivalensi) adalah final jika tidak mungkin untuk lulus dari kondisi kelas tertentu ke status milik kelas lain.
Misalnya, semua pola hidup (perilaku) tidak tergantung pada kecepatan. Juga, mereka tidak bergantung pada kecepatan sirkuit, yang akhirnya berhenti, dan dalam satu keadaan.
Selanjutnya, penulis membuat koneksi antara skema SI di satu sisi, dan dengan skema distribusi semi-modular, sekuensial, di sisi lain. Dan sebagai kesimpulan, ia mengutip daftar sifat sirkuit yang luar biasa yang tidak tergantung pada kecepatan.

Poin pertama sangat menarik. Itu hanya mengatakan bahwa sirkuit independen kecepatan tidak bergantung pada keterlambatan elemen logika. Sayangnya, teks tidak secara eksplisit menyatakan alasan untuk kesimpulan ini. Mungkin inilah alasan kesalahpahaman selanjutnya tentang istilah SI. Pada kenyataannya, kesimpulan ini sepenuhnya benar. Pada awal bab 10, penulis memberikan aturan untuk menghitung keadaan selanjutnya.

Transisi rangkaian ke keadaan berikutnya adalah hasil dari pengalihan output dari beberapa elemen logika (atau output dari beberapa elemen). Yaitu, interval waktu antara penciptaan kondisi untuk beralih elemen logika (eksitasi) dan switching itu sendiri tidak dibatasi oleh apa pun. Dan periode waktu seperti itu adalah penundaan elemen logis. Artinya, sejak awal, penulis melanjutkan dari asumsi bahwa keterlambatan elemen logika dapat menjadi besar secara sewenang-wenang. Memang, berikut ini ditulis sedikit lebih jauh.

Nah, untuk menghilangkan semua keraguan, kutipan dari halaman pertama bab 10.

Dengan demikian, fakta yang tak terbantahkan didirikan: kemandirian dari keterlambatan elemen logika bukanlah properti dari sirkuit, tetapi properti dari model di mana sirkuit ini diselidiki. Artinya, sirkuit apa pun, SI atau bukan SI, diselidiki dengan cara yang sama seperti yang dijelaskan oleh R. Miller, tidak tergantung pada keterlambatan elemen logika. Pada saat yang sama, sirkuit apa pun dapat diselidiki dalam model dengan penundaan terbatas. Dalam model seperti itu, himpunan keadaan yang dapat diterima adalah himpunan bagian dari himpunan keadaan yang dapat diterima ketika mempertimbangkan skema yang sama dalam model dengan penundaan elemen tak terbatas. Saat memeriksa sirkuit dalam model dengan penundaan elemen terbatas, sirkuit mungkin independen kecepatan dan pada saat yang sama tergantung pada penundaan elemen.
Dengan demikian, ternyata independensi rangkaian dari keterlambatan elemen logika sama sekali tidak terhubung dengan properti SI. Kemudian muncul pertanyaan: apa gunanya memperkenalkan definisi kemerdekaan dari kecepatan? Memang, perhatikan dua pola dan perilakunya.
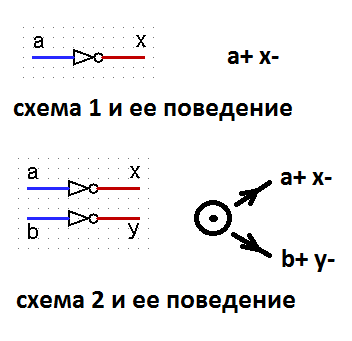
Sinyal a, b untuk kedua sirkuit adalah input, sinyal x, y adalah output. Kedua skema menerapkan perilaku yang sangat masuk akal. Tetapi pada saat yang sama, sirkuit 1 tidak tergantung pada kecepatan, dan sirkuit 2 tidak memiliki sifat seperti itu. Ya, kita dapat mengatakan bahwa definisi SI diperkenalkan tanpa membagi sinyal menjadi input dan output. Tetapi pemisahan sinyal oleh penulis seperti itu tersirat, dan ada komentar dalam teks tentang ini.
Makna dan kewajaran pengenalan definisi properti SI diungkapkan hanya sehubungan dengan properti semi-modularitas. Untuk sirkuit dengan sifat semi-modularitas, setiap sinyal dapat menghilangkan eksitasi hanya melalui switching-nya. Skema non-semi-modular selama implementasi fisik penuh dengan gangguan dan kondisi metastabil. Hanya skema semi-modular yang dapat dianggap stabil.
Tetapi hubungan antara sifat semi-modularitas dan independensi dari kecepatan adalah satu sisi. Artinya, skema semi-modular tidak tergantung pada kecepatan, tetapi sebaliknya tidak benar. Sirkuit SI mungkin tidak semi-modular. Artinya, properti yang benar-benar penting membagi sirkuit berdasarkan stabilitas adalah semi-modularitas. Penting untuk dipahami bahwa sirkuit semi-modular juga dapat bergantung pada keterlambatan elemen logika, jika kita mempertimbangkannya dalam model dengan waktu tunda yang terbatas.
Tapi itu belum semuanya. Properti semi-modularitas juga didefinisikan untuk sirkuit otonom, yaitu, tanpa membagi sinyal menjadi input dan output. Karena itu, skema pilihan bebas (perilaku) tidak memenuhi kriteria semi-modularitas. Sementara itu, skema ini dapat menjadi stabil seperti semi-modular. Misalnya, skema 2 di atas bukan semi-modular, tetapi dalam hal stabilitas, sama sekali tidak kalah dengan skema 1, yang semi-modular.
Ada jalan keluar dari kebuntuan ini. Buku J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno, A. Yakovlev "Sintesis Logika untuk Pengendali dan Antarmuka Asinkron" mendefinisikan definisi properti persistensi keluaran (OP).

Ini adalah properti OP yang merupakan properti aktual yang memisahkan skema (perilaku) menjadi stabil dan tidak stabil. Ini adalah properti OP yang harus menggantikan properti SI. Tidak boleh dilupakan bahwa independensi dari keterlambatan elemen logika adalah properti dari model di mana sirkuit (perilaku) dipelajari. Dan sirkuit OP juga dapat bergantung pada penundaan elemen jika dipertimbangkan dalam model penundaan terbatas.
Terlepas dari semua kritik sebelumnya, tidak ada keluhan terhadap R. Miller. Tidak ada kesalahan logis dalam karyanya. Kesalahan lebih dari setengah abad kesalahan lebih terletak pada pembaca yang salah mengartikan karya R. Miller.
Dan akhirnya, kesimpulan yang menyenangkan dari hal tersebut di atas. STG Behavioral Model menyediakan waktu tak terbatas untuk elemen-elemen logika. Aturan untuk mengubah tanda, mengekstraksi tabel kebenaran dirumuskan dari asumsi elemen penundaan tanpa batas. Oleh karena itu, setiap sirkuit yang diperoleh dengan menghitung fungsi logis menggunakan STG (baik menggunakan tabel kebenaran atau langsung menggunakan grafik) jelas tidak tergantung pada keterlambatan elemen logis. Benar, harus dipahami bahwa manipulasi lebih lanjut dengan skema yang dihasilkan dapat menyebabkan hilangnya kualitas yang berharga ini.