Bukti yang ditemukan bahwa semua perubahan adalah campuran urutan dan peluang

Semua deskripsi perubahan adalah campuran unik dari peluang dan determinisme, menurut bukti radikal dari "hipotesis lemah" Pinsker

Bayangkan sebuah taman di mana semua bunga dunia tumbuh - anggrek halus, bunga matahari yang menjulang tinggi, bunga lilin kaktus Carnegie dan perbungaan bau amorphophallus titanic . Sekarang bayangkan bahwa semua keanekaragaman tanaman ini telah turun menjadi hanya dua pilihan, dan dengan menyilangkannya, Anda dapat menghasilkan yang lainnya.

Ini adalah sifat dari salah satu bukti paling radikal yang diperoleh dalam beberapa tahun terakhir. Itu dibuat oleh Tim Austin , seorang ahli matematika dari University of California di Los Angeles. Tetapi alih-alih bunga, karya Austin dikaitkan dengan salah satu objek yang paling banyak dipelajari dalam matematika: deskripsi matematis tentang perubahan.

Deskripsi ini, yang dikenal sebagai sistem dinamis , berlaku untuk segala sesuatu mulai dari pergerakan planet hingga fluktuasi pasar saham. Di mana pun sistem dinamis muncul, matematikawan ingin memahami dasarnya. Dan salah satu fakta dasar adalah bahwa sistem dinamik kompleks yang arbitrer dapat dibagi menjadi elemen acak dan deterministik.

Pertanyaan ini adalah subjek dari “hipotesis lemah” Pinsker, yang pertama kali dirumuskan pada tahun 1970-an. Bukti hipotesis yang diajukan oleh Austin memberikan metode pemikiran intuitif yang elegan tentang segala macam fenomena yang tidak jelas. Dia menunjukkan bahwa, pada dasarnya, masing-masing sistem dinamis ini adalah campuran antara kebetulan dan determinisme.

Nasib dan peluang

Sistem dinamis dimulai dengan beberapa data input, misalnya, dengan posisi bandul, menerapkan aturan tertentu, misalnya, hukum gerak Newton, dan menghasilkan hasil tertentu, misalnya, posisi bandul dalam satu detik. Yang penting, sistem dinamis memungkinkan Anda mengulangi proses ini: Anda dapat mengambil posisi pendulum baru, menerapkan aturan yang sama, dan mendapatkan posisinya di detik lain.

Sistem dinamis juga murni matematis. Anda dapat memilih nomor awal, menerapkan aturan "kalikan jumlahnya dengan dua" dan dapatkan yang baru. Sistem ini juga memungkinkan Anda untuk memasukkan jumlah total kembali ke penangan aturan dan mendapatkan lebih banyak nomor.

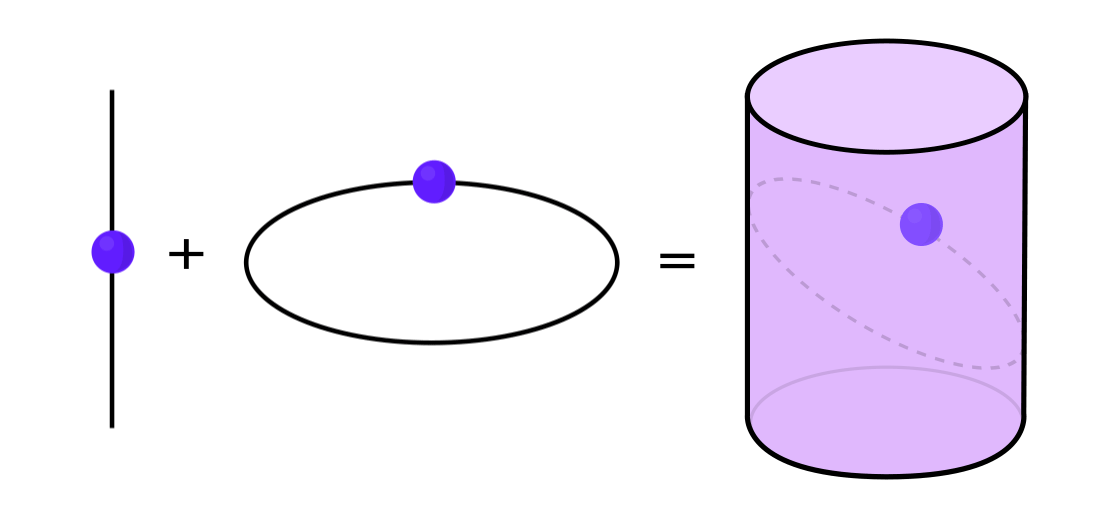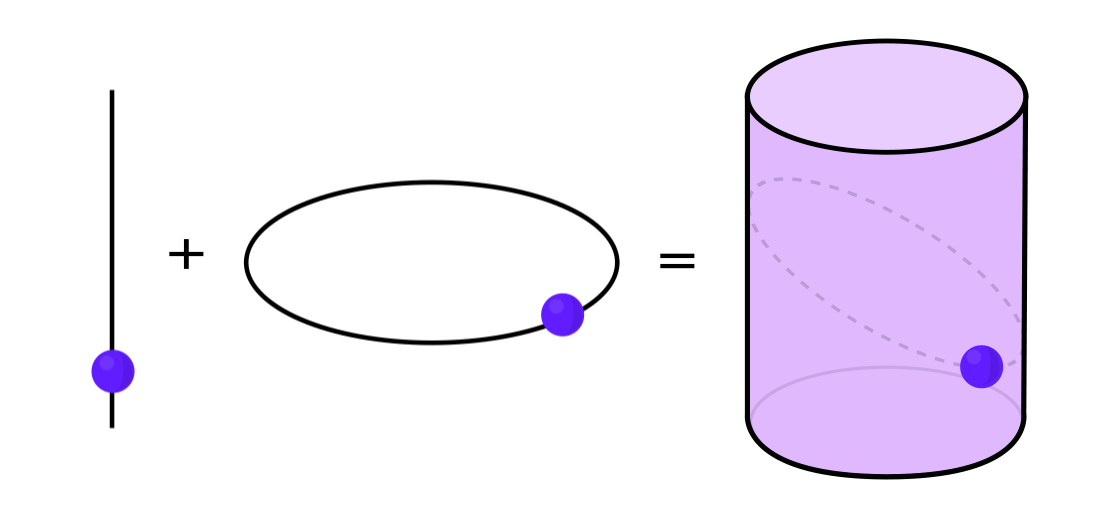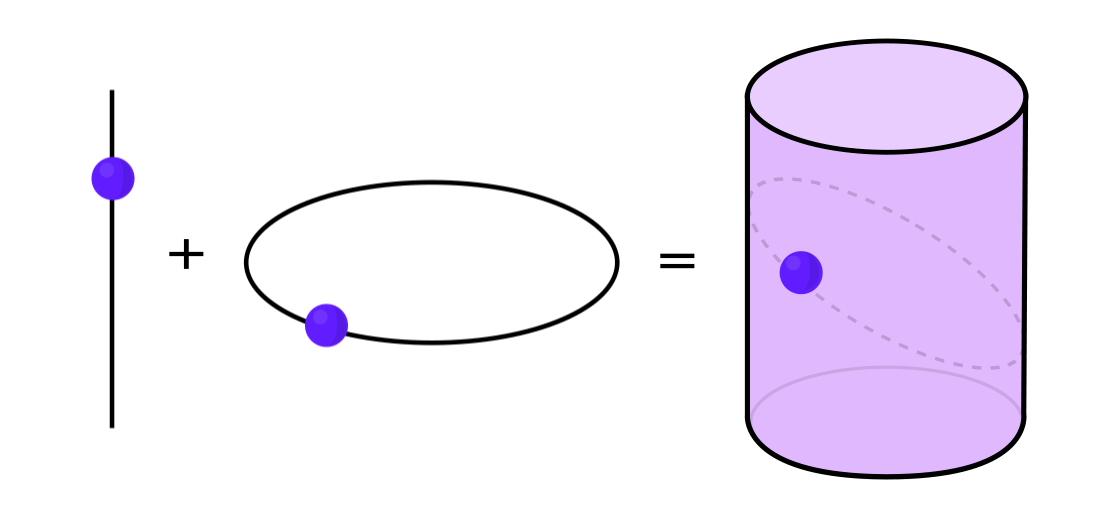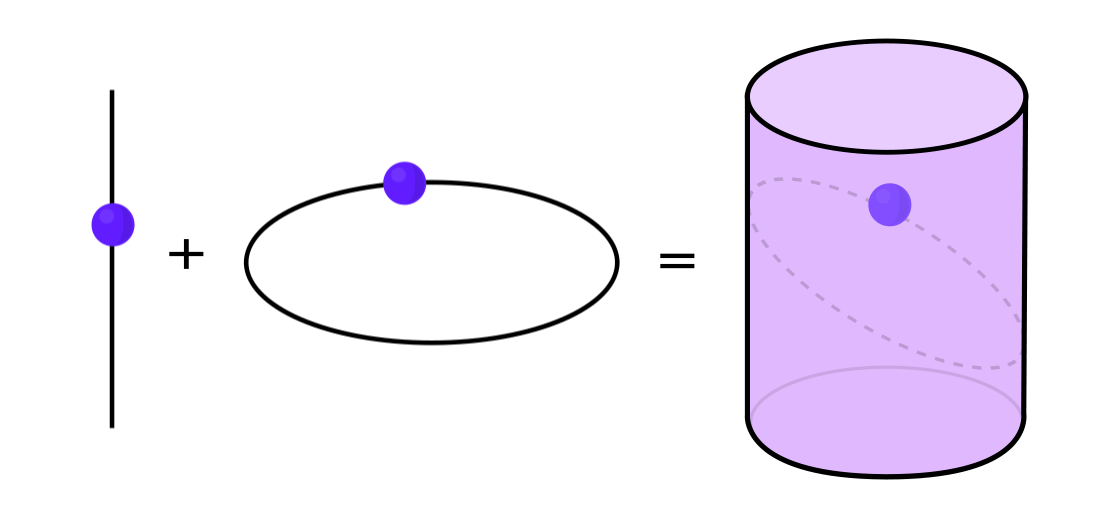
Beberapa jenis sistem dinamis dapat dinyatakan sebagai kombinasi dari dua sistem dinamis yang lebih sederhana. Kedua sistem ini bekerja secara independen satu sama lain, tetapi mereka dapat digabungkan untuk membentuk yang lebih kompleks. Misalnya, bayangkan sistem dinamis yang memindahkan titik di sepanjang permukaan silinder. Anda memasukkan posisi titik, menerapkan aturan, dan mendapatkan titik lain.

Sistem ini dapat dibongkar menjadi dua yang sederhana. Yang pertama adalah sistem dinamis yang memindahkan titik di sekitar lingkaran. Yang kedua adalah sistem yang memindahkan titik naik dan turun secara vertikal. Dengan menggabungkan dua sistem - gerakan melingkar dan gerakan lurus - kami memperoleh gerakan titik yang lebih kompleks di sepanjang silinder.



"Daripada mempelajari keseluruhan sistem dinamis secara keseluruhan, Anda perlu memecahnya menjadi beberapa bagian, bagian kecil yang masuk akal untuk dipelajari," kata Catherine Lindsay , seorang ahli matematika di Boston College.

Ada dua kandidat alami untuk peran blok bangunan ini. Yang pertama adalah sistem dinamik sepenuhnya deterministik, seperti contoh pendulum kami. Jika Anda mengetahui posisi bandul di beberapa titik waktu, Anda dapat memperkirakannya kapan saja di masa mendatang.


Jean-Paul Tuveno pada tahun 1975, dua tahun sebelum perumusan hipotesis lemah Pinsker

Tipe kedua dari sistem dinamis sepenuhnya acak. Misalnya, bayangkan sistem dinamis dengan aturan ini: lempar koin. Jika ada elang, ambil langkah ke kiri; jika berekor, benar. Jalur terakhir akan sepenuhnya acak, yaitu, bahkan jika Anda tahu segalanya tentang jalur sebelumnya, informasi ini tidak akan membantu Anda memprediksi langkah selanjutnya.

Beberapa sistem dinamis benar-benar acak, yang lain sepenuhnya deterministik, dan sebagian besar berada di antara keduanya - mereka adalah hibrida dari keduanya. Misalnya, bayangkan versi jalan acak kami yang sedikit dimodifikasi. Kami berjalan di sepanjang jalan di sepanjang tepi bunga yang ditanam, dan warnanya juga acak. Aturannya tetap sama: jika elang jatuh, ke kiri; jika berekor, benar. Apa yang akan menjadi urutan warna bunga?

Pertama, Anda mengatakan secara acak. Lagi pula, warna itu sendiri dipilih secara acak, dan gerakan Anda juga acak. Namun, setelah Anda melewati satu bunga, kemungkinan bahwa Anda akan melewatinya di masa depan meningkat, hanya karena Anda tidak jauh dari itu. Urutan warna bunga tidak akan sepenuhnya acak.

"Jika Anda berdiri di sebelah merah, itu meningkatkan kemungkinan bahwa dalam dua langkah Anda akan bertemu merah lagi, karena mungkin Anda melangkah ke kiri, lalu ke kanan, dan kembali ke tempat yang sama," kata Austin.

Seperti "jalan acak melalui lanskap acak" menghasilkan output - urutan warna - sebagian acak dan sebagian tidak. Pada tahun 1960, ahli matematika Mark Pinsker menyarankan bahwa kelas besar tertentu dari sistem dinamis memiliki sifat berikut: mereka adalah campuran dari sistem dinamika acak dengan yang deterministik.

Dugaan Pinsker berlaku untuk kelas sistem dinamis yang memiliki sifat bersama yang penting. Poin-poin di dalamnya tidak beranjak jauh dari satu sama lain dan tidak menyusut selama pengembangan sistem. Lebih tepatnya, jika Anda menggambar lingkaran di sekitar satu set titik di ruang Anda (ruang tersebut mungkin seperti permukaan silinder), mulailah pengembangan sistem dinamis untuk periode waktu yang lama, dan kemudian buat lingkaran di sekitar set poin yang dihasilkan, kemudian area tempat titik-titik tersebut berada. akhirnya, bertepatan dengan area yang mereka tempati di awal. Sistem semacam itu disebut "pengawetan takaran"

"Jika hipotesis asli Pinsker benar, itu akan menjadi deskripsi yang menakjubkan tentang dunia," kata Assaf Naor , seorang ahli matematika di Universitas Princeton. Tapi Pinsker salah. Pada tahun 1973, Donald Ornstein menyangkal hipotesisnya. "Kata-katanya terlalu ambisius," kata Brina Kra , seorang ahli matematika di Universitas Northwestern.

Dalam matematika, sering terjadi bahwa setelah hipotesis umum dibantah, matematikawan mencoba merumuskan versi yang lebih sederhana. Pada 1977, ahli matematika Jean-Paul Tuveno mengusulkan hipotesis Pinsker yang lemah. Dia melunakkan formulasi asli, menunjukkan bahwa sistem dinamis yang ada di pikiran Pinker adalah hasil dari menggabungkan sistem acak murni dengan sistem yang hampir sepenuhnya deterministik.

Penyempurnaan "hampir" membedakan hipotesis Tuveno dari hipotesis Pinsker. Dia bermaksud bahwa sistem deterministik sederhana harus memiliki sedikit jejak peluang. Jejak ini mungkin menghilang kecil, tetapi harus ada di sana. Dan sementara dia, kata Tuveno, ide Pinsker akan berhasil.

"Itu dekat dengan hipotesis asli, dan Tuveno menunjukkan bahwa jika demikian, maka hipotesis akan memiliki sejumlah besar aplikasi luar biasa," kata Naor.

Pada dekade-dekade berikutnya, matematikawan tidak mencapai banyak keberhasilan dalam membuktikan hipotesis lemah Pinsker. Kurangnya kemajuan membuat Tuveno berpikir bahwa kata-katanya yang lemah pun ternyata salah. "Pada satu titik, saya berpikir bahwa semuanya akan menjadi kebalikannya, bahwa itu tidak akan bersifat universal," katanya.

Dan kemudian Tim Austin muncul.

Solusi langkah

Untuk membuktikan hipotesis lemah Pinsker, perlu untuk menemukan cara yang tepat untuk menyaring sistem yang dinamis - yang akan memungkinkannya untuk memisahkan bagian acak dan hampir deterministik. Pekerjaan sebelumnya telah menetapkan bahwa akan paling sulit untuk mengisolasi elemen dengan sedikit keacakan.

"Faktor acak kecil jauh lebih sulit untuk ditangkap, dan bagian utama dari bukti menemukan cara untuk mendeteksi struktur acak kecil," kata Tuveno.


Tim Austin, ahli matematika di University of California, Los Angeles

Austin berhasil berurusan dengan elemen acak kecil dari sistem dinamis dengan mengubah perspektif. Sistem dinamis beroperasi pada ruang kontinu, seperti titik yang bergerak di sepanjang permukaan silinder, atau pendulum yang berayun di ruang. Dalam ruang-ruang ini, titik bergerak sepanjang busur kontinu sesuai dengan aturan sistem dinamik. Juga, sistem ini bekerja pada jumlah langkah yang tak terbatas - mereka dapat bertindak selamanya.

Tetapi dalam buktinya, Austin meninggalkan ruang halus terus menerus dan lupa tentang pekerjaan abadi sistem dinamik. Sebagai gantinya, ia mulai menganalisis apa yang akan terjadi jika mereka diizinkan untuk bekerja pada waktu yang berbeda, seperti sejuta langkah. Karena itu ia menerapkan metode yang ditemukan oleh Tuveno.

"Kontribusi utama Tuveno adalah dia menyadari bahwa jika Anda melakukan langkah-langkah matematika yang benar dengan garis akhir yang panjang," Anda dapat membuktikan sifat-sifat sistem dinamis, kata Austin. "Kontribusi utama saya adalah bahwa saya membuktikan apa yang dibutuhkan untuk garis panjang."

Austin membayangkan sistem dinamis yang mengeluarkan urutan satu dan nol. Jika sistem dinamis melempar koin, maka mudah dibayangkan: ekor akan menjadi 1, dan elang akan menjadi 0. Tetapi sistem dinamis apa pun dapat digunakan untuk menghasilkan urutan biner dengan hanya membagi ruang di mana ia bekerja menjadi dua (tidak harus sama) bagian.



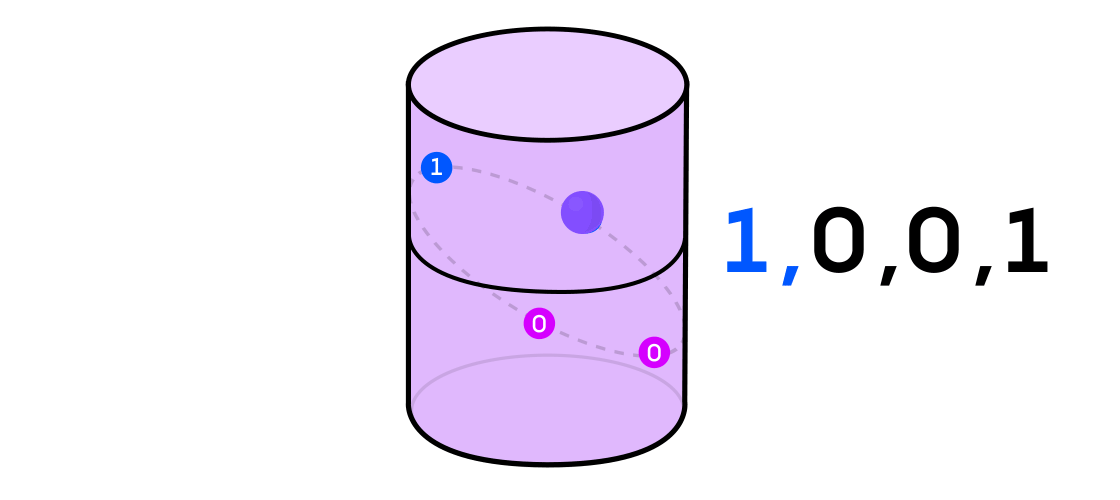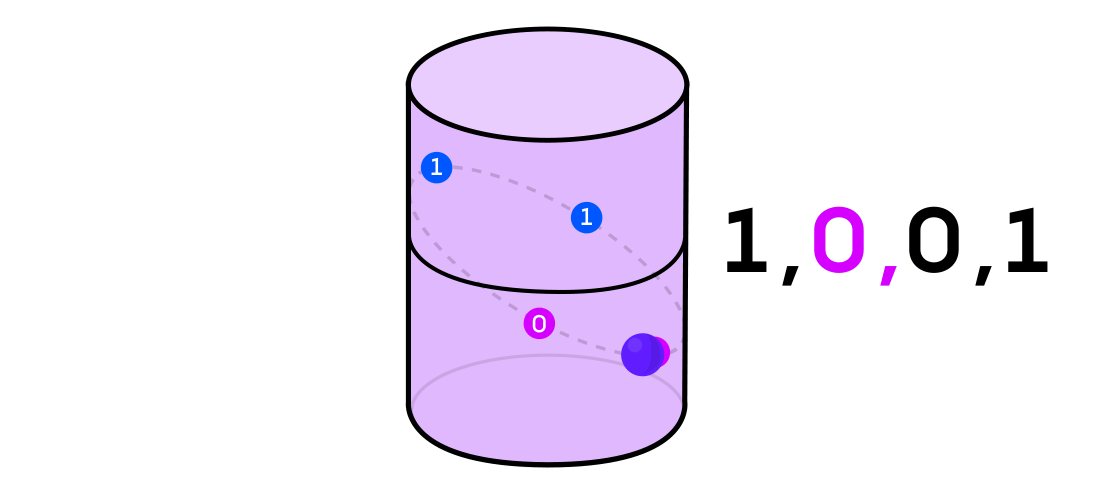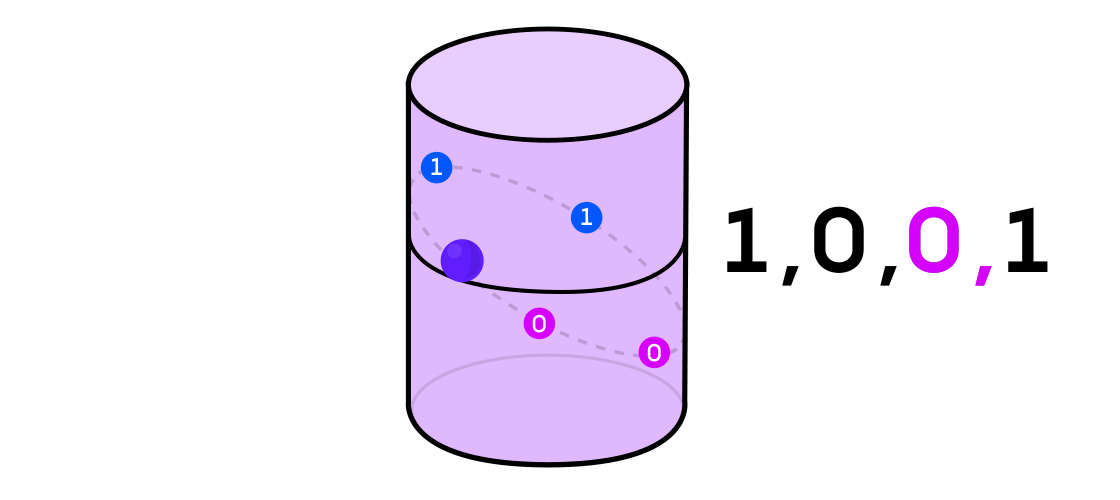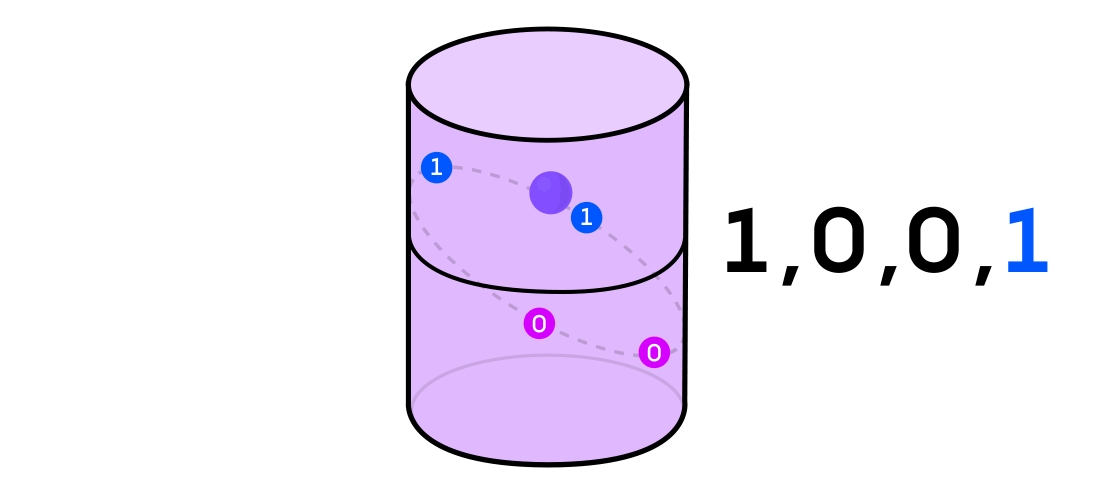
Kembali ke contoh sistem dinamis pada silinder, jika titiknya ada di satu bagian silinder, Anda menyatakan nilai output sistem 1, dan jika di sisi lain, maka 0.

Austin menganalisis urutan biner ini menggunakan alat teori informasi yang disebut Hamming Cubes . Bayangkan sebuah kubus simpul yang dihubungkan oleh tepian. Angka-angka biner ditugaskan untuk setiap titik - katakanlah, 001 atau 101. Setiap kali, ketika beralih dari satu titik ke titik lain, salah satu dari tiga digit berubah.

Hamming kubus bisa jauh lebih rumit daripada kita, mereka dapat memiliki lebih banyak tepi dan simpul dalam dimensi lebih dari tiga - tetapi mereka semua memiliki properti, karena jarak antara dua simpul - atau jumlah tepi yang harus Anda tuju pergi dari satu titik ke titik yang lain sama dengan jumlah tempat di mana garis-garis informasi yang sesuai dengan titik-titik ini dibedakan. Oleh karena itu, 000 terletak pada jarak satu sisi dari 001, dua sisi dari 011 dan tiga dari 111.



Untuk mengisolasi elemen acak dan deterministik yang membentuk sistem dinamis yang kompleks, Austin berpikir tentang seberapa sering sistem dinamis dapat menghasilkan urutan nol tertentu dan yang diwakili pada kubus Hamming. Dia membuktikan bahwa urutan ini didistribusikan dalam sebuah kubus dengan cara tertentu. Mereka terakumulasi dalam sejumlah kecil subkelompok kubus - dan kluster ini mencerminkan determinisme sistem - namun, mereka terdistribusi secara acak di antara urutan dalam kelompok ini, yang mencerminkan keacakan sistem.

Bundaran seperti itu diperlukan untuk menyelesaikan masalah yang tidak menyerah pada serangan langsung.

"Apa yang mengejutkan saya bukanlah kebenaran atau kepalsuan dari hipotesis lemah Pinsker, tetapi bagaimana ternyata terbukti, karena tugas ini tampak begitu berbahaya," kata Lewis Bowen, seorang ahli matematika di University of Texas di Austin. "Sebelum bukti muncul, kita, pada umumnya, tidak tahu apakah ini bisa dilakukan sama sekali."

Hasil Austin memberikan struktur dasar untuk berbagai sistem dinamis. Untuk ahli matematika, yang sering berputar di antara benda-benda yang tampaknya saling berhubungan, tidak jelas bagaimana buktinya memberikan geografi yang tepat. Sekarang mereka memiliki panduan untuk sistem yang dinamis ini, meskipun masih belum diketahui penemuan seperti apa yang akan terjadi.

"Matematikawan selalu tertarik pada blok bangunan yang membentuk apa pun," kata Lindsay. "Bukti Austin adalah hasil yang sangat baik, yang kemungkinan memiliki banyak aplikasi dalam matematika murni, tetapi saya tidak bisa mengatakan apa yang akan terjadi."