Geekly articles weekly

Analisis wavelet. Bagian 3

Pendahuluan


Saat melakukan analisis CWT menggunakan pustaka PyWavelets (perangkat lunak open source gratis yang dirilis di bawah lisensi MIT), ada masalah dengan memvisualisasikan hasilnya. Program uji visualisasi yang diusulkan oleh pengembang ditunjukkan dalam daftar berikut:

Daftar
import pywt import numpy as np import matplotlib.pyplot as plt t = np.linspace(-1, 1, 200, endpoint=False) sig = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4))) widths = np.arange(1, 31) cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5') plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto', vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max()) # doctest: +SKIP plt.show() # doctest: +SKIP

Saat bekerja dengan wavelet yang kompleks, misalnya dengan 'cmor1-1.5', program menghasilkan kesalahan:

 File"C:\Users\User\AppData\Local\Programs\Python\Python36\lib\site-packages\matplotlib\image.py", line 642, in set_data raise TypeError("Image data cannot be converted to float") TypeError: Image data cannot be converted to float

Kesalahan ini, serta kesulitan dalam memilih skala (lebar) untuk memberikan resolusi temporal yang diperlukan, menyulitkan, terutama bagi pengguna pemula, untuk mempelajari analisis CWT, yang mendorong saya untuk menulis artikel pendidikan ini.

Tujuan dari publikasi ini adalah untuk mempertimbangkan penggunaan modul visualisasi scaleogram baru untuk analisis sinyal sederhana dan khusus, serta ketika menggunakan metode normalisasi, penskalaan dan sintesis logaritmik, yang memberikan informasi tambahan dalam analisis deret waktu.

Artikel ini menggunakan informasi dari publikasi "Pengantar wavelet untuk analisis data" . Dalam daftar contoh yang diberikan dalam publikasi, kesalahan diperbaiki, dan setiap daftar contoh dibawa ke formulir selesai, yang memungkinkan untuk digunakan tanpa pengenalan dengan yang sebelumnya. Untuk analisis wavelet sinyal khusus, data dari database sampel PyWavelets digunakan.

Skalogram wavelet adalah representasi dua dimensi dari data satu dimensi. Waktu diplot pada sumbu X, dan skala pada sumbu Y adalah hasil dari transformasi wavelet dari sinyal yang sesuai dengan amplitudo sinyal pada waktu X. Nilai analitik dari tampilan grafik sinyal adalah bahwa resolusi waktu ditampilkan pada sumbu Y, yang memberikan informasi tambahan tentang sifat dinamis dari sinyal.

Wavelet - Skalogram Sinyal Sederhana


1. Gelombang kosinus dengan amplop Gaussian (Mengganti wavelet. Anda dapat mempelajari ketergantungan resolusi waktu pada skala):

Daftar
 from numpy import* from pylab import* import scaleogram as scg import pywt #  ,        #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) p1=10; periodic1 = cos(2*pi/p1*time) * exp(-((time-ns/2)/200)**2) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(periodic1); ax1.set_xlim(0, len(time)) ax1.set_title("   ") fig1.tight_layout() ax2 = scg.cws(periodic1, scales=scales, figsize=(6.9,2.9)); txt = ax2.annotate("p1=%s"%p1, xy=(100, 10), bbox=dict(boxstyle="round4", fc="w")) tight_layout() print("    :", scg.get_default_wavelet(), "(", pywt.ContinuousWavelet(scg.get_default_wavelet()).family_name, ")") show()


Fungsi wavelet untuk konversi sinyal: cmor1-1.5 (wavelet Morlet Kompleks)





Sinyal periodik sekarang muncul dalam bentuk strip kontinu horisontal pada titik Y = p1, intensitasnya bervariasi tergantung pada amplitudo sinyal periodik.

Ada beberapa ketidakjelasan dalam pendeteksian, karena bandwidth tidak sama dengan nol, ini disebabkan oleh fakta bahwa wavelet tidak mendeteksi satu frekuensi, melainkan sebuah band. Efek ini dikaitkan dengan bandwidth wavelet.

2. Tiga pulsa ditambahkan secara berurutan dengan periode yang meningkat (Untuk mempertimbangkan variasi periodik pada skala yang berbeda: analisis multi-resolusi):

Daftar
 from numpy import* import pandas as pd from pylab import* import scaleogram as scg #          #       'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) pulses = zeros(ns, dtype=float32) steps = linspace(0, ns, 8) periods = [10, 20, 40] for i in range(0,3): step_mask = (time > steps[i*2+1]) & (time < steps[i*2+2]) pulses += cos(2*pi/periods[i]*time) * step_mask fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(pulses); ax1.set_xlim(0, len(time)); ax1.set_title("     "); ax1.set_xlabel("Time") fig1.tight_layout() ax2 = scg.cws(pulses, scales=scales, figsize=(7,3)) for i in range(0, 3): txt = ax2.annotate("p%d=%ds"%(i+1,periods[i]), xy=(steps[i*2]+20, periods[i]), bbox=dict(boxstyle="round4", fc="w")) ax2.plot(steps[i*2+1]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) ax2.plot(steps[i*2+2]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5) tight_layout() show()






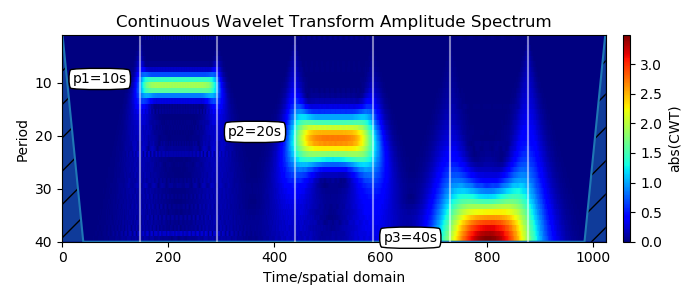
Impuls muncul di tempat yang diharapkan Y, sesuai dengan periodisitasnya, mereka dilokalisasi dalam frekuensi dan waktu. Awal strip dan ujung sesuai dengan denyut nadi.
Bandwidth berskala dengan panjang periode. Ini adalah properti transformasi wavelet yang terkenal: ketika skala meningkat, resolusi waktu berkurang. Ini juga dikenal sebagai pertukaran antara waktu dan frekuensi. Ketika Anda melihat spektrogram jenis ini, Anda melakukan banyak analisis resolusi.

3. Tiga osilasi periodik dari frekuensi yang berbeda secara bersamaan (Wavelet - analisis dapat membedakan komponen sinyal dengan frekuensi, jika perbedaannya signifikan):

Daftar
 from numpy import* import pandas as pd from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) allwaves = np.zeros(ns, dtype=np.float32) periods = [10, 20, 40] for i in range(0,3): allwaves += cos(2*np.pi/periods[i]*time) fig1, ax1 = subplots(1, 1, figsize=(6.5,2)); lines = ax1.plot(allwaves); ax1.set_title("  ") ax1.set_xlim(0, len(time)); ax1.set_xlabel("") fig1.tight_layout() ax2 = scg.cws(allwaves, scales=scales, figsize=(7,2)) tight_layout() show()






4. Sinyal periodik non-sinusoidal (Perbedaan dalam transformasi wavelet dari sinyal gelombang segitiga dengan periode 30 detik dari yang sebelumnya dianggap dipertimbangkan):

Daftar
 from numpy import* from pylab import* import scipy.signal import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) ptri = 30.0 # period in samples raising = 0.8 # fraction of the period raising triangle = scipy.signal.sawtooth(time/ptri*2*pi, raising) # plot the signal fig1, ax1 = subplots(1, 1, figsize=(7,3)); lines = ax1.plot(triangle); ax1.set_xlim(0, len(time)) ax1.set_title("triangle wave increasing 80% of the time with a 30s period") fig1.tight_layout() # and the scaleogram ax2 = scg.cws(triangle, scales=scales, figsize=(7,3)); txt = ax2.annotate("first harmonic", xy=(100, 30), bbox=dict(boxstyle="round4", fc="w")) txt = ax2.annotate("second harmonic", xy=(100, 15), bbox=dict(boxstyle="round4", fc="w")) tight_layout() show()






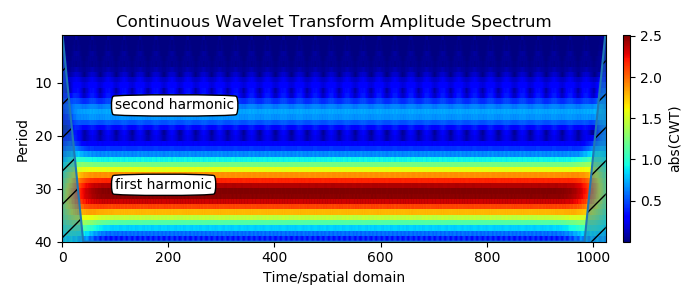
Sebuah band besar adalah harmonik pertama. Harmoni kedua terlihat persis pada setengah nilai periode harmonik pertama. Ini adalah hasil yang diharapkan untuk sinyal non-sinusoidal berkala. Elemen vertikal fuzzy muncul di sekitar harmonik kedua, yang lebih lemah dan memiliki amplitudo 1/4 dari yang pertama untuk bentuk gelombang segitiga.

5. Impuls halus (Gaussians) mirip dengan struktur data nyata. (Contoh ini menunjukkan cara menggunakan analisis wavelet untuk mendeteksi perubahan sinyal yang dilokalkan dari waktu ke waktu):

Serangkaian pulsa halus dengan nilai sigma yang berbeda:

  • 2 cdot sigma1=2
  • 2 cdot sigma2=10
  • 2 cdot sigma3=$2

Lebar pulsa:

  •  omega1=2
  •  omega2=$2
  •  omega3=$10

Daftar
 from numpy import* from pylab import* import scaleogram as scg scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') ##    1  /  ns = 1024 time = arange(ns) scales = scg.periods2scales(arange(1, 40)) #       s1=1; s2=5; s3=10 events = [ns*0.1, ns*0.3, ns*0.7] bumps = exp(-((time-events[0])/s1)**2) + exp(-((time-events[1])/s2)**2) + \ exp(-((time-events[2])/s3)**2) #      w1=1; w2=5; w3= 50 steps = ((time > events[0]-w1) & (time < events[0]+w1)) + \ ((time > events[1]-w2) & (time < events[1]+w2)) + \ ((time > events[2]-w3) & (time < events[2]+w3)) #   fig1, (ax1, ax2) = subplots(1, 2, figsize=(11, 2)); ax1.set_title("Bumps"); ax2.set_title("Steps") lines = ax1.plot(bumps); ax1.set_xlim(0, len(time)) lines = ax2.plot(steps); ax2.set_xlim(0, len(time)) fig1.tight_layout() #   scales_bumps = scg.periods2scales(arange(1, 120, 2) ) fig2, (ax3, ax4) = subplots(1, 2, figsize=(14,3)); ax3 = scg.cws(bumps, scales=scales_bumps, ax=ax3) ax4 = scg.cws(steps, scales=scales_bumps, ax=ax4) for bmpw, stepw in [(2*s1, 2*w1), (2*s2,2*w2), (2*s3, 2*w3)]: ax3.plot(ax3.get_xlim(), bmpw*ones(2), 'w-', alpha=0.5) ax4.plot(ax4.get_xlim(), stepw*ones(2), 'w-', alpha=0.5) fig2.tight_layout() show()






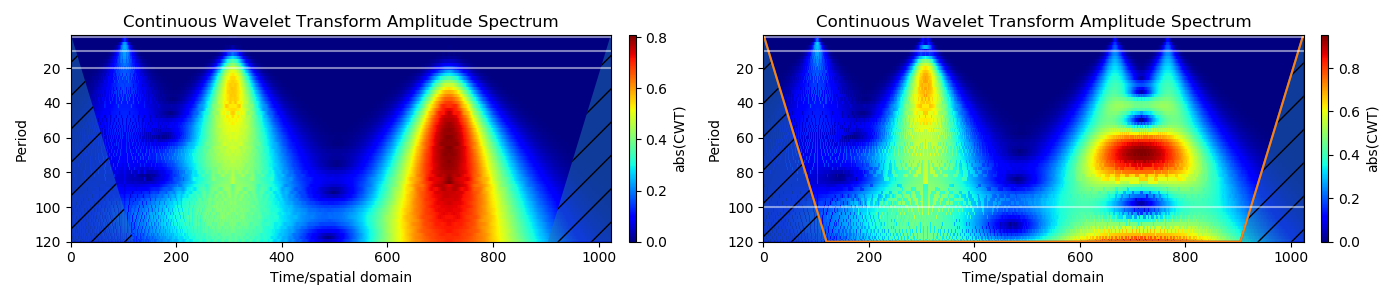
Pulsa diskrit menciptakan struktur kerucut pada sialogram, yang juga dikenal sebagai pengaruh kerucut. Impuls halus (Gaussians) mirip dengan struktur data nyata dan membuat kerucut meluas ke skala besar. Garis panduan horizontal berhubungan kira-kira dengan periode waktu (2 detik, 10 detik, 20 detik). Oleh karena itu, pulsa ini mirip dengan sinyal periodik dengan satu periode.

6. Kebisingan (Menampilkan kebisingan pada sialogram):

Daftar
 from numpy import* from pylab import* import scaleogram as scg import random scg.set_default_wavelet('cmor1-1.5') #          #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #    1  /  ns = 1024 time =arange(ns) scales = scg.periods2scales( arange(1, 40) ) noise =random.sample(range(ns), ns) fig1, ax1 = plt.subplots(1, 1, figsize=(6.2,2)); ax1.set_title("  ") lines = ax1.plot(time, noise) ax1.set_xlim(0, ns) fig1.tight_layout() ax2 = scg.cws(noise, scales=scales, figsize=(7,2)) tight_layout() show()






Noise biasanya ditampilkan sebagai satu set elemen, dan beberapa penyimpangan mungkin terlihat seperti objek data nyata, jadi ketika menggunakan data nyata, Anda harus berhati-hati dan, jika perlu, periksa tingkat kebisingan. Jadwal atas akan berbeda setiap kali program dimulai.

Skalogram Wavelet dari Sinyal Khusus


Database PyWavelets berisi dua puluh sinyal transformasi wavelet khusus yang akan berguna untuk studi dan pengembangan. Oleh karena itu, saya akan memberikan daftar yang memungkinkan Anda untuk melakukan analisis wavelet dari semua dua puluh sinyal:

Daftar
 #!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np from pylab import* import scaleogram as scg import pywt signals = pywt.data.demo_signal('list') signal_length=1024 for signal in signals: if signal in ['Gabor', 'sineoneoverx']: x = pywt.data.demo_signal(signal) else: x = pywt.data.demo_signal(signal, signal_length) times=[] signals=[] for time, sig in enumerate(x.real): times.append(time) signals.append(sig) scg.set_default_wavelet('cmor1-1.5') scales = scg.periods2scales( arange(1, 40) ) fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9)); lines = ax1.plot(signals); ax1.set_xlim(0, len(times)) ax1.set_title("%s"%signal) fig1.tight_layout() ax2 = scg.cws(signals, scales=scales, figsize=(6.9,2.9)); tight_layout() show()


Saya hanya akan memberikan satu hasil dari transformasi wavelet dari sinyal Doppler:





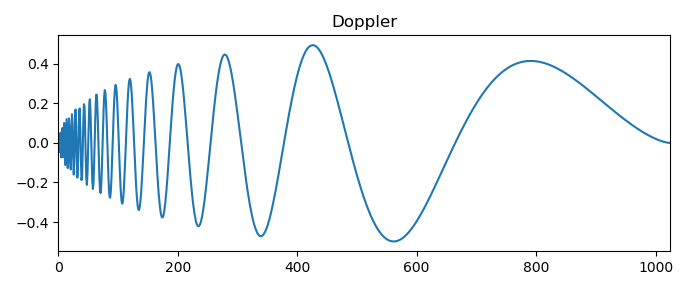
Varietas yang paling umum dari sinyal sederhana dan khusus dipertimbangkan, yang memungkinkan kita untuk beralih menggunakan skalogram untuk menyelesaikan beberapa masalah analisis deret waktu.

Skalog garis waktu wavelet


1. Data kesuburan CDC di AS 1969-2008 (data kesuburan berisi fitur periodik, baik dalam skala tahunan dan yang lebih kecil):

Daftar
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) fig = figure(figsize=(12,2)) lines = plot(births.index, births.values/1000, '-') xlim(datetime_lim) ylabel("Nb of birthes [k]"); title("Total births per day in the US (CDC)"); xlim = xlim() ax = scg.cws(births, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()






Garis horizontal muncul dengan frekuensi sekitar 7 hari. Nilai-nilai tinggi muncul di dekat batas skala, yang merupakan perilaku normal pemrosesan wavelet. Efek-efek ini dikenal sebagai kerucut pengaruh, itulah sebabnya masker (opsional) menutupi area ini.

2. Normalisasi (Menghapus mean - births_normed = births-births.mean () adalah wajib, jika tidak, batas data dianggap sebagai tahap yang membuat banyak deteksi berbentuk kerucut palsu):

Daftar
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() ax = scg.cws(births_normed, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day") set_x_yearly(ax, len(births)) show()




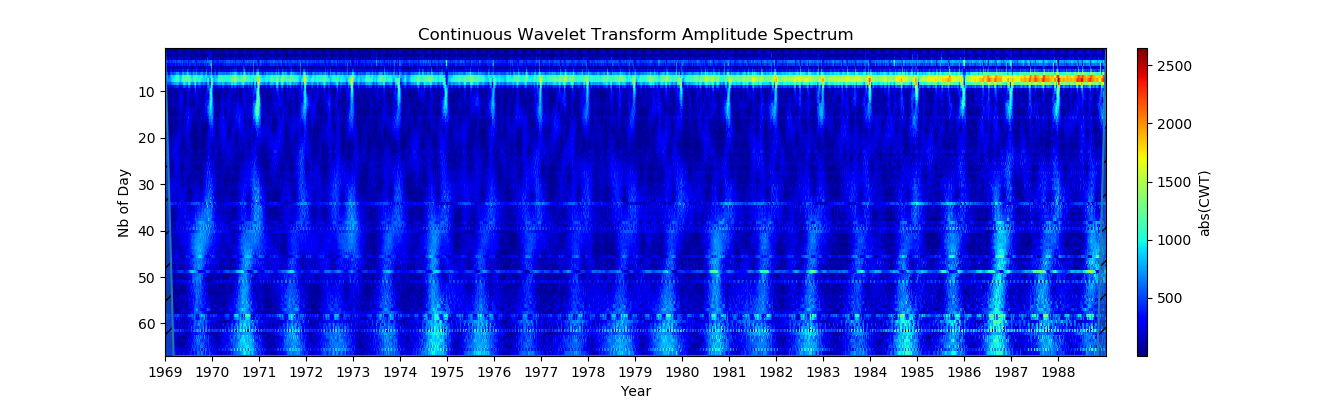
3. Perubahan skala dalam amplitudo (Untuk melihat objek tahunan, gunakan period2scales () skala di sepanjang sumbu Y ditentukan).

Daftar
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 5), xlabel="Year", ylabel="Nb of Day", clim=(0, 2500)) set_x_yearly(ax, len(births)) show()




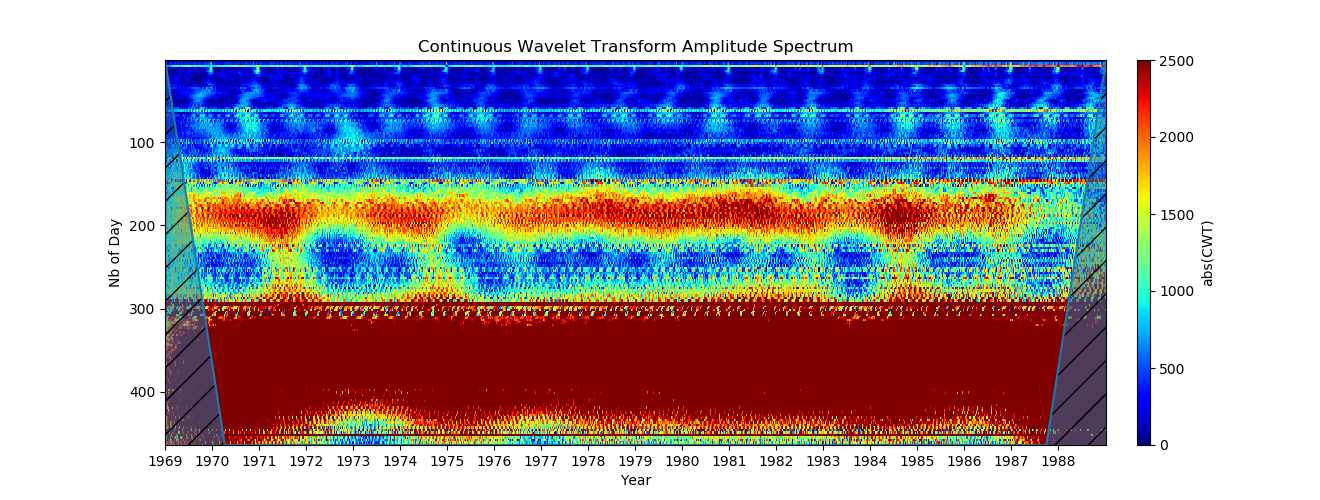
Kisaran amplitudo dari peta warna (sumbu Y) sekarang ditetapkan oleh clim = (0,2500). Nilai tepat untuk amplitudo osilasi tergantung pada wavelet, tetapi akan tetap dekat dengan urutan nilai aktual. Ini jauh lebih baik, sekarang kita melihat variasi tahunan dengan sangat baik, juga sekitar 6 bulan!

4. Menggunakan skala logaritmik (Untuk melihat periode kecil dan besar pada saat yang sama, lebih baik menggunakan skala logaritmik pada sumbu Y. Ini dicapai dengan menggunakan opsi xscale = log.)

Daftar
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() scales = scg.periods2scales(np.arange(1, 365+100, 3)) ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) print("Number of available days:", len(births_normed)) show()




Hasilnya jauh lebih baik, tetapi sekarang piksel pada nilai periode rendah memanjang di sepanjang sumbu Y.

5. Distribusi seragam pada skala logaritmik (Untuk mendapatkan distribusi seragam pada skala, nilai periode harus didistribusikan secara merata dan kemudian dikonversi ke nilai skala, seperti yang ditunjukkan di bawah ini :):

Daftar
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #  CWT  ,       cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bboxf = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowpropsf = dict(facecolor='yellow', shrink=0.05) text = ax.annotate("unusual\nfeature", xy=(365*6, 15), xytext=(365*3, 50), bbox=bboxf, arrowprops=arrowpropsf) show()




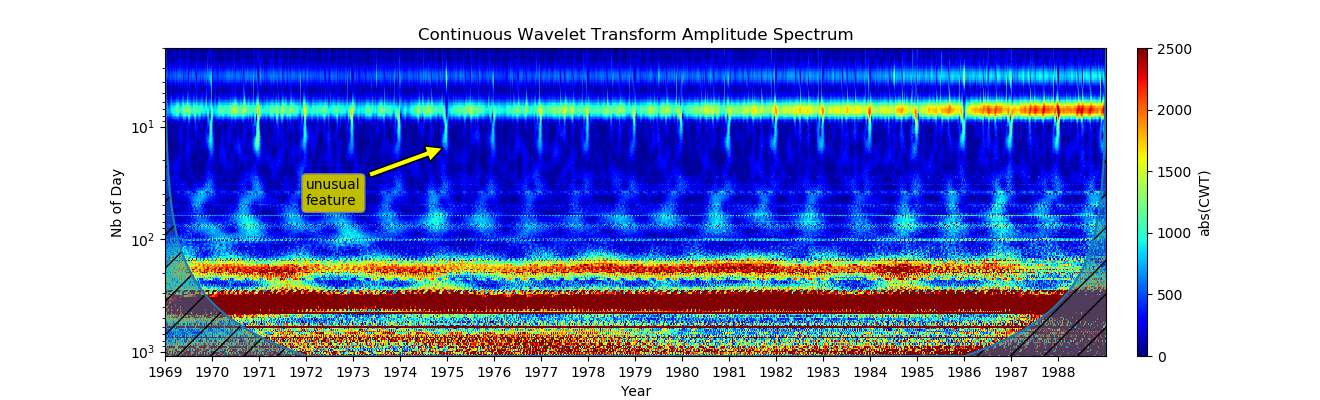
Kita bisa melihat perubahan sinyal di semua skala. Sialogram ditampilkan setiap tahun dalam periode yang sama.

6. Sorot bagian dari garis waktu (Memeriksa data perantara antara tanda garis waktu untuk mencari artefak atau data yang hilang.):

Daftar
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) #    : 1974-1976 fig = figure(figsize=(12,4)) lines =plot(births.index, births.values/1000, '-') xlim(pd.to_datetime("1974-01-01"), pd.to_datetime("1976-01-01")) ylabel("Nb of birthes [k]"); title("Total births per day bw 1974 and 1976"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1974-1969)*365, (1976-1969)*365 ) show()





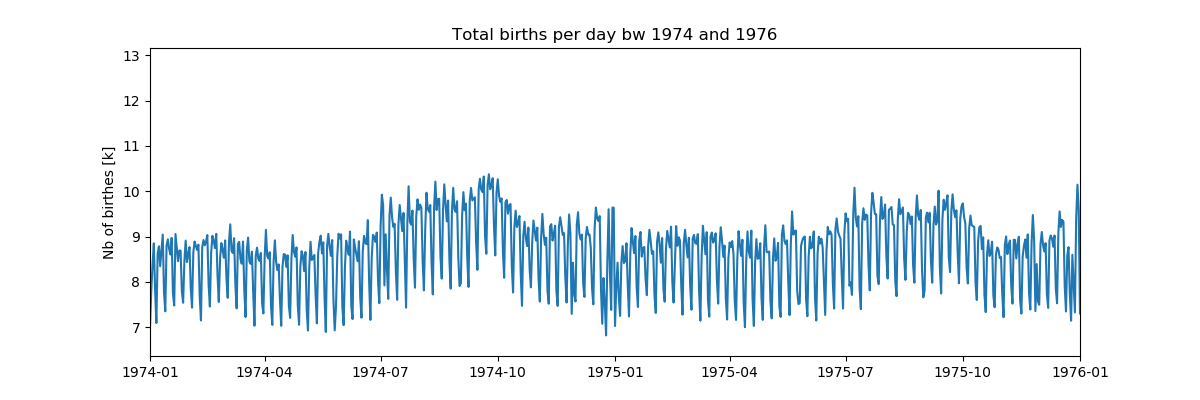
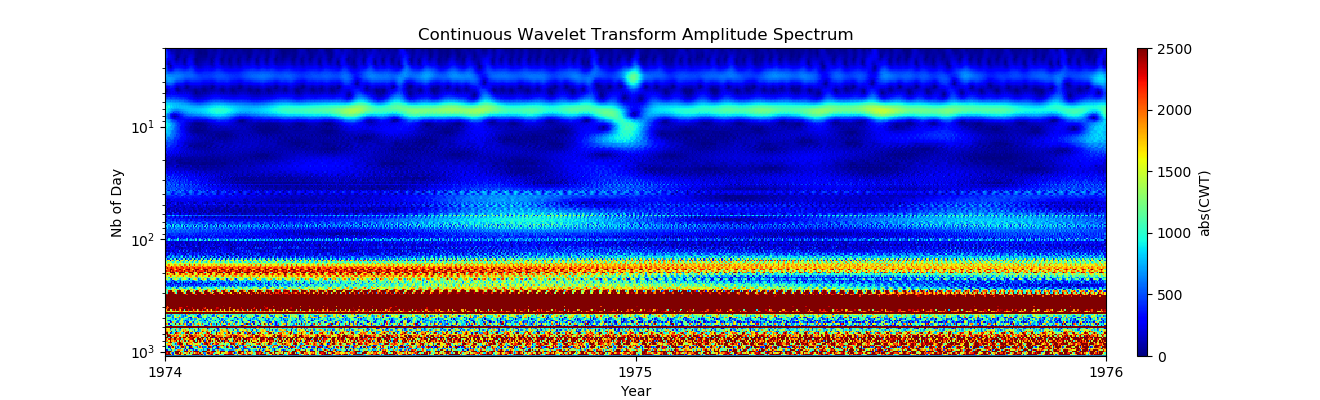Pada pandangan pertama, pola mingguan terlihat sangat merata, tetapi sesuatu terjadi pada Hari Natal, mari kita lihat periode ini lagi:

Daftar
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) # :  1975    1976  fig = figure(figsize=(12,4)) lines = plot(births.index, births.values/1000, '.-') xlim(pd.to_datetime("1974-12-01"), pd.to_datetime("1975-02-01")) ylabel("Nb of birthes [k]"); title("Total births per day : 2 monthes zoom"); #      ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) xlim = ax.set_xlim( (1975-1969)*365-30, (1975-1969)*365+30 ) show()






Sekarang sudah jelas bahwa ini adalah efek akhir tahun:

  • Natal: 23/24 Desember 2525 menunjukkan jumlah kelahiran yang rendah secara abnormal, dan hari-hari ini menyimpang dari jadwal mingguan;
  • Ada data untuk bulan Desember, yang konsisten dengan keberadaan beberapa nilai untuk tanggal yang terpengaruh pada tanggal 1 dan 2 Januari, tanggal-tanggal ini biasanya kurang dari kejadian pribadi

7. Sintesis (Sialogram dibangun dari data yang dinormalisasi, dengan keterbacaan yang lebih baik untuk semua skala):

Daftar
 import pandas as pd import numpy as np from pylab import* import scaleogram as scg import pywt from pandas.plotting import register_matplotlib_converters register_matplotlib_converters() #          #    'cmor1-1.5' #scg.set_default_wavelet('cmor1-1.5') #scg.set_default_wavelet('cgau5') #scg.set_default_wavelet('cgau1') #scg.set_default_wavelet('shan0.5-2') #scg.set_default_wavelet('mexh') df = pd.read_csv("births.csv") #   df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)] #   datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce') df.insert(0, 'datetime', datetime) datetime_lim = [ df.datetime.min(), df.datetime.max() ] years_lim = [ df.datetime.min().year, df.datetime.max().year ] births = df[['datetime', 'births']].groupby('datetime').sum().squeeze() def set_x_yearly(ax, days, start_year=1969): xlim = (np.round([0, days]) / 365).astype(np.int32) ticks = np.arange(xlim[0], xlim[1]) ax.set_xticks(ticks*365) ax.set_xticklabels(start_year + ticks) births_normed = births-births.mean() #        log-Y-axis :-) scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200)) #        log-Y-axis :-) cwt = scg.CWT(births_normed, scales=scales) ax = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", clim=(0,2500), yscale='log') set_x_yearly(ax, len(births)) bbox = dict(boxstyle="round", facecolor="w", edgecolor="0.5") bbox2 = dict(boxstyle="round", facecolor="y", edgecolor="0.5") arrowprops = dict(facecolor='white', shrink=0.05) arrowprops2 = dict(facecolor='yellow', shrink=0.05) for period, label in [ (3.5, "half a week"), (7, "one week"), (365/2, "half a year"), (365, "one year"), (365*2.8, "long trends")]: text = ax.annotate(label, xy=(365*5.5, period), xytext=(365*2, period), bbox=bbox, arrowprops=arrowprops) text = ax.annotate("end of year\neffect", xy=(365*6, 15), xytext=(365*3, 50), bbox=bbox2, arrowprops=arrowprops2) text = ax.annotate("increase in\nvariations *amplitude*", xy=(365*18.5, 7), xytext=(365*14, 50), bbox=bbox2, arrowprops=arrowprops2) show()




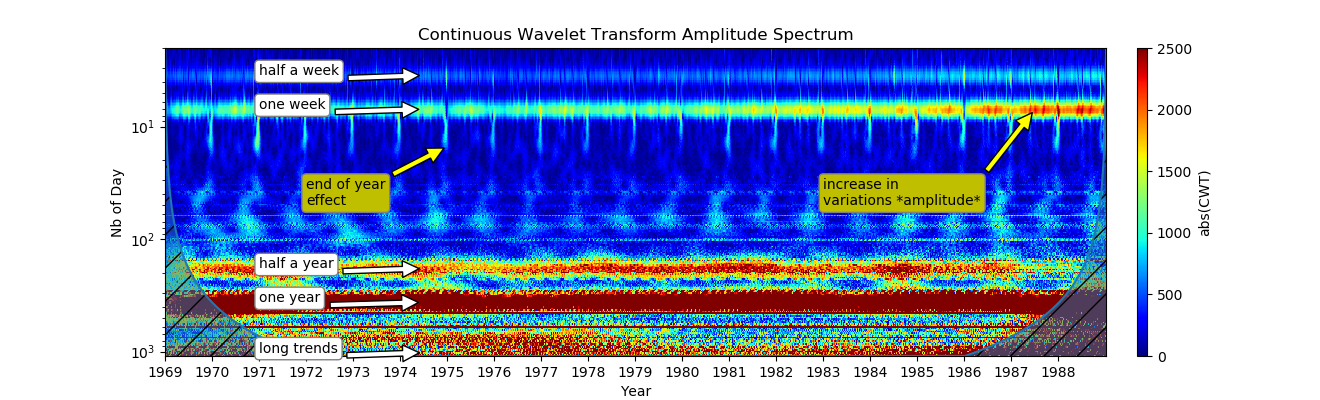CWT mengungkapkan banyak informasi dalam waktu singkat:

Variasi mingguan yang menunjukkan kebiasaan rumah sakit telah ada selama beberapa dekade;

Pada tahun 80-an ada peningkatan dalam indikator mingguan, yang mungkin disebabkan oleh perubahan dalam kebiasaan kerja rumah sakit, perubahan kesuburan, atau perubahan sederhana dalam populasi;

Band setengah tahun kedua jelas harmonik kedua. Pola kabur muncul di zona dari 3 hingga 1 bulan, yang mungkin karena harmonik ketiga, karena fluktuasi tahunan sangat kuat. Mungkin juga disebabkan oleh efek liburan pada kesuburan dan mungkin memerlukan studi lebih lanjut;

Efek akhir tahun tercatat pada Natal dan 1 Januari. Yang ini mungkin tetap tidak terlihat dengan metode frekuensi lain.

Kesimpulan:


Dalam publikasi ini, kami melihat bagaimana bentuk dasar dari variasi sinyal diterjemahkan menjadi skalogram. Contoh dataset yang dipesan waktu kemudian digunakan untuk menunjukkan langkah demi langkah bagaimana CWT diterapkan pada data standar.

Teknik di atas dapat diperluas untuk menganalisis lalu lintas jaringan dan untuk mendeteksi perilaku objek yang tidak biasa. CWT adalah alat yang ampuh yang semakin banyak digunakan sebagai input ke jaringan saraf dan dapat digunakan untuk membuat fungsi baru untuk mengklasifikasikan atau mendeteksi anomali.

Setiap contoh diimplementasikan sebagai program independen, yang memungkinkan Anda untuk memilih contoh untuk tugas Anda, tanpa mempelajari contoh sebelumnya dan selanjutnya. Pengguna dapat mencoba fungsi wavelet apa saja dari daftar yang diberikan di awal setiap program, misalnya, seperti mexh atau gaus5. Misalnya masing-masing 1:





PS Untuk penggunaan praktis daftar, saya akan memberikan versi modul yang digunakan di dalamnya:

 >>> import scaleogram; print(scaleogram .__version__) 0.9.5 >>> import pandas; print(pandas .__version__) 0.24.1 >>> import numpy; print(numpy .__version__) 1.16.1 >>> import matplotlib; print(matplotlib .__version__) 3.0.2

Untuk kumpulan data independen dalam file * .csv, saya berikan struktur data (dalam satu kolom):
tahun, bulan, hari, jenis kelamin, kelahiran
1969,1,1, F, 4046
1969,1,1, M, 4440
1969,1,2 , F,
4454 1969.1.2, M, 4548
...
Untuk panda versi 0.24.1, Anda harus mendaftarkan konverter matplotlib secara eksplisit.

Untuk mendaftarkan konverter:

 from pandas.plotting import register_matplotlib_converters register_matplotlib_converters()

Source: https://habr.com/ru/post/id454240/

More articles:


All Articles