ARA: algoritma untuk menemukan jumlah maksimum poin pada garis lurus

Baru-baru ini, saya menemukan masalah klasik untuk wawancara: mencari jumlah maksimum poin berdiri di garis lurus (di pesawat, bilangan bulat koordinat). Gagasan pencarian lengkap segera muncul di benak saya, yang memiliki kompleksitas waktu yang jelas dalam O (n ^ 2), tetapi bagi saya tampaknya ada sesuatu yang lain, setidaknya beberapa alternatif dalam O (n * log (n)) . Setelah setengah jam, bahkan sesuatu yang lebih baik ditemukan!



_{Pernyataan masalah yang lebih terperinci dengan contoh input-output ada di GeeksForGeeks dan LeetCode}

Pada awalnya saya perhatikan bahwa Anda dapat dengan mudah menyelesaikan masalah hanya untuk garis horizontal atau vertikal, menambahkan X / Y dari setiap titik dalam kamus. Dan bagaimana perbedaan jalur lainnya? Hanya lereng? .. Tapi ini bisa diperbaiki!

Jadi, saya memutuskan bahwa mungkin untuk memeriksa seluruh daftar poin beberapa kali dengan memutarnya. Dan solusi dalam O (n) diperoleh! Meskipun dengan koefisien yang besar. Saya sangat berharap bahwa saya tidak menciptakan sepeda :)

# ***  *** #   #    = 180/ROT_COUNT  # #      12, #  180*4    (6% ), #  180*20   (0% ). # ó    . #     - . ROT_COUNT = 180*10 #  #        , #       1 / MULT_COEF. #    4  . #   MULT_COEF   ROT_COUNT. # ó    - . #     - . MULT_COEF = 2 ** 3 angles = list(map(lambda x: x*180.0/ROT_COUNT, range(ROT_COUNT))) def mnp_rotated(points, angle): """Returns Maximum Number of Points on the same line with given rotation""" #   rad = math.radians(angle) co = math.cos(rad) si = math.sin(rad) #      counts = {} for pair in points: #    nx = pair[0]*co - pair[1]*si #       , #      #       #      nx = int(nx * MULT_COEF) #   if nx in counts: counts[nx] += 1 else: counts[nx] = 1 #    return max(counts.values()) def mnp(points): """Returns Maximum Number of Points on the same line""" res = 0 best_angle = 0 #      for i in angles: current = mnp_rotated(points, i) #  ,     if current > res: res = current best_angle = i return res 

Divisualisasikan, tampilannya seperti ini:
_{GIF buatan saya yang pertama, jangan dimarahi :)}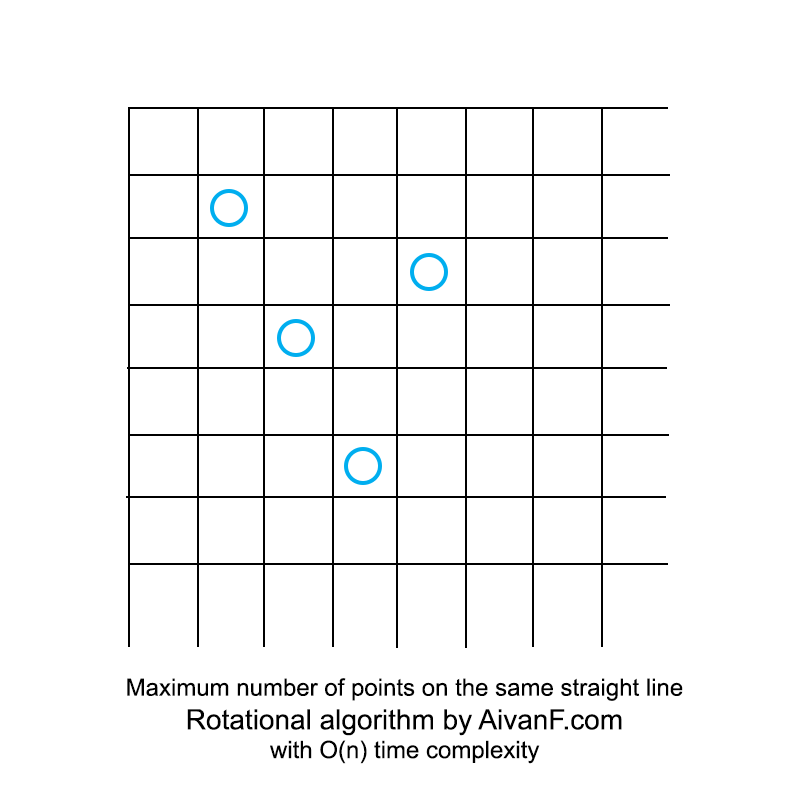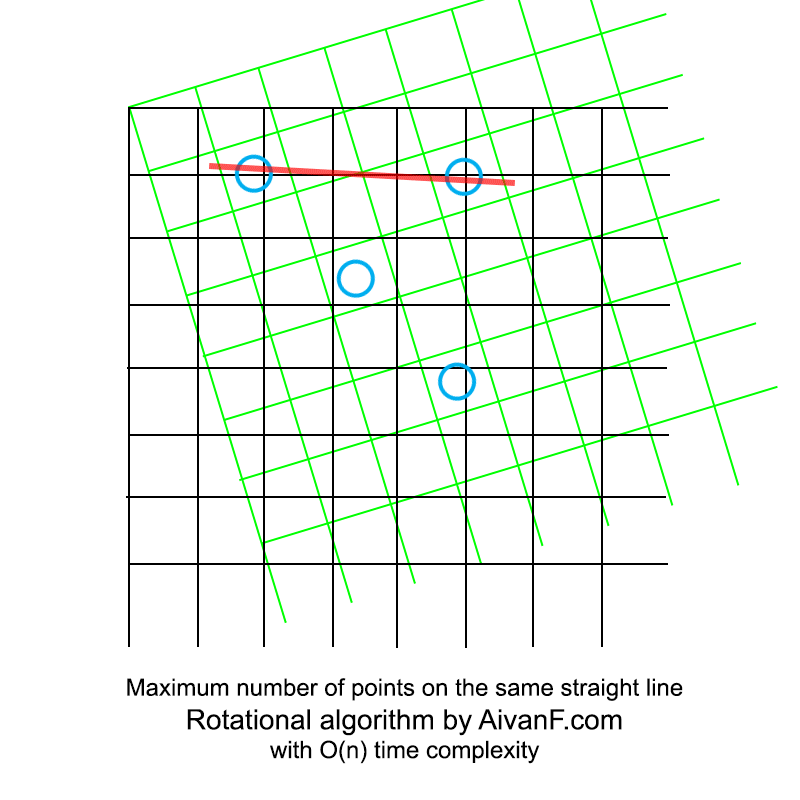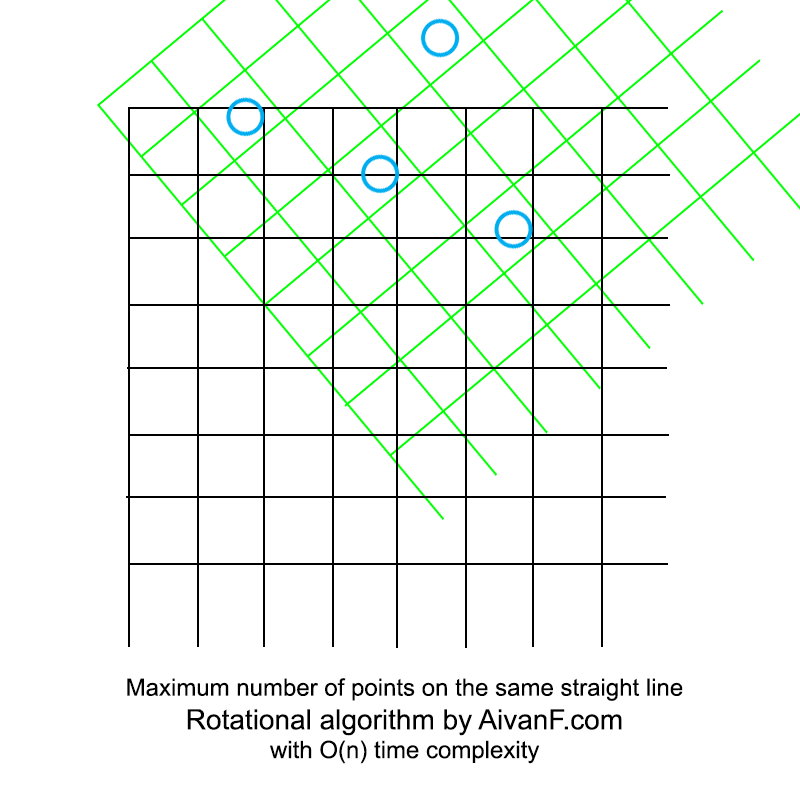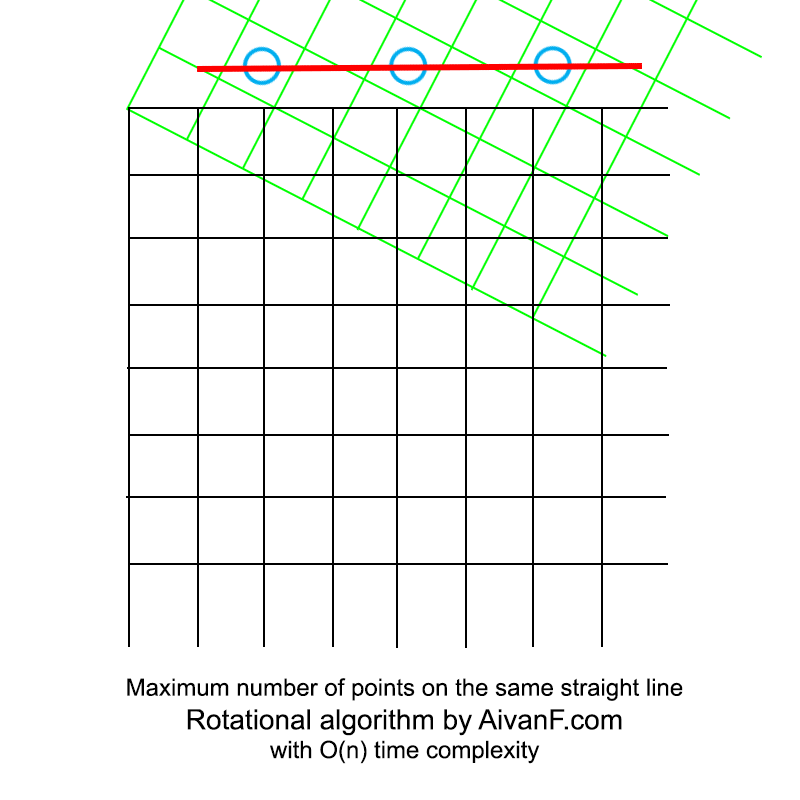



Sangat menarik untuk dicatat bahwa implementasi selanjutnya dari pencarian lengkap mengambil lebih banyak baris kode.

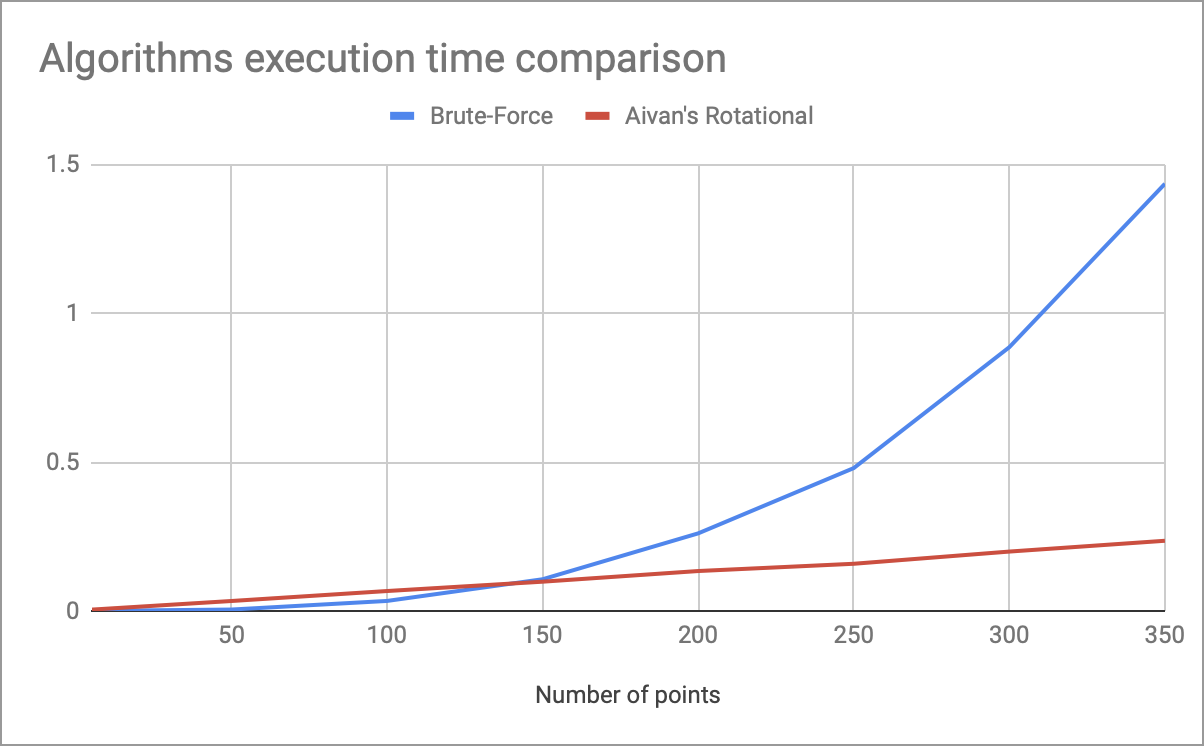
Grafik dengan pengukuran runtime dari algoritma rotasi saya dan penghitungan lengkap tergantung pada jumlah poin di header.


Sekitar 150 poin menunjukkan keunggulan kompleksitas linier dalam waktu (dengan koefisien yang digunakan dalam kode di atas). Alhasil, algoritma ini memiliki kelemahan sebagai berikut:

• Akurasinya tidak absolut.
• Runtime pada set poin kecil itu panjang.
  _{Secara umum, ini mudah dikoreksi dengan pemilihan koefisien yang kompeten: untuk set sederhana, ROT_COUNT = 36 daripada 2000 sudah cukup, yang mempercepat kode 50+ kali.}

Dan keuntungan seperti itu:

• Ini bekerja dengan tenang dengan koordinat fraksional.
• Kompleksitas waktu linear, yang terlihat pada set data besar.

Tabel dengan pengukuran tersedia di sini . Seluruh kode sumber proyek dengan algoritma dan berbagai pemeriksaan ada di GitHub .

Perbarui Saya ingin sekali lagi mencatat bahwa algoritma ini memiliki kelebihan dan kekurangan, saya tidak menganjurkannya sebagai pengganti yang ideal untuk brute force, saya hanya menggambarkan alternatif yang mungkin menarik, yang dalam beberapa kasus mungkin lebih tepat.