Memecahkan Teka-Teki Silang Jepang dengan P̶y̶t̶h̶o̶̶n̶ Rust dan WebAssembly

Cara membuat pemecah nonogram untuk Python, tulis ulang ke Rust untuk menjalankannya langsung di peramban melalui WebAssembly.

TL; DR

Mulai

Tentang teka-teki silang Jepang (nonogram) di Habré sudah ada beberapa pos. Contoh
dan satu lagi .

Gambar dienkripsi dengan angka yang terletak di sebelah kiri baris, serta di atas kolom. Jumlah angka menunjukkan berapa banyak kelompok sel hitam (atau warnanya, untuk teka-teki silang warna) dalam baris atau kolom yang sesuai, dan angka itu sendiri - berapa banyak sel yang digabungkan yang berisi masing-masing grup ini (misalnya, kumpulan tiga angka - 4, 1, dan 3) berarti bahwa dalam baris ini ada tiga kelompok: yang pertama - dari empat, yang kedua - dari satu, yang ketiga - dari tiga sel hitam). Dalam teka-teki silang hitam dan putih, grup harus dipisahkan oleh setidaknya satu sel kosong, dalam warna aturan ini hanya berlaku untuk grup satu warna, dan grup multi-warna dapat diberi jarak yang dekat (sel kosong juga dapat berada di sepanjang tepi baris). Penting untuk menentukan lokasi kelompok sel.

Salah satu sudut pandang yang paling umum diterima adalah bahwa teka-teki silang yang "benar" hanya dapat disebut dengan teka-teki yang diselesaikan dengan cara yang "logis". Ini biasanya disebut metode solusi, di mana ketergantungan antara baris dan / atau kolom yang berbeda tidak diperhitungkan. Dengan kata lain, solusi adalah urutan keputusan independen dari baris atau kolom individu sampai semua sel terisi (lebih lanjut tentang algoritma di bawah). Misalnya, hanya nonograms yang dapat ditemukan di situs web http://nonograms.org/ ( http://nonograms.ru/ ). Nonogram dari situs ini telah dikutip sebagai contoh dalam artikel Memecahkan Teka-Teki Warna Jepang dengan Kecepatan Cahaya . Untuk tujuan perbandingan dan verifikasi, pemecah masalah saya juga menambahkan dukungan untuk mengunduh dan mengurai teka-teki silang dari situs ini (terima kasih kepada KyberPrizrak untuk izin menggunakan bahan dari situsnya).

Namun, konsep nonograms dapat diperluas ke masalah yang lebih umum, ketika metode "logis" yang biasa mengarah pada jalan buntu. Dalam kasus seperti itu, kita harus membuat asumsi tentang warna sel dan, setelah membuktikan bahwa warna ini mengarah ke kontradiksi, tandai warna yang berlawanan untuk sel ini. Urutan langkah-langkah tersebut dapat (jika Anda memiliki kesabaran) memberi kami semua solusi. Artikel ini terutama membahas penyelesaian kasus teka-teki silang yang lebih umum.

Python

Sekitar satu setengah tahun yang lalu, saya tidak sengaja menemukan sebuah artikel yang menggambarkan metode untuk menyelesaikan satu baris (ternyata kemudian, metode ini agak lambat).

Ketika saya menerapkan metode ini dalam Python (bahasa kerja utama saya) dan menambahkan pembaruan berurutan dari semua baris, saya melihat bahwa semua ini tidak diselesaikan dengan sangat cepat. Setelah mempelajari materiil, ternyata pada topik ini ada banyak pekerjaan dan implementasi yang menawarkan pendekatan berbeda untuk tugas ini.

Tampak bagi saya bahwa pekerjaan yang paling ambisius pada analisis berbagai implementasi solver dilakukan oleh Jan Wolter, menerbitkan di situsnya (yang, sejauh yang saya tahu, tetap menjadi repositori publik terbesar nonograms di Internet), sebuah studi terperinci yang berisi banyak informasi dan tautan yang dapat membantu dalam membuat solver Anda sendiri.

Mempelajari banyak sumber (akan ada di akhir artikel), saya secara bertahap meningkatkan kecepatan dan fungsionalitas pemecah saya. Sebagai hasilnya, saya kecanduan dan saya terlibat dalam implementasi, refactoring, debugging algoritma selama sekitar 10 bulan di waktu luang dari pekerjaan.

Algoritma inti

Pemecah yang dihasilkan dapat diwakili dalam bentuk empat tingkat keputusan:

• ( line ) linear solver: pada input, garis sel dan garis deskripsi (petunjuk), pada output, garis yang diselesaikan sebagian. Dalam solusi python, saya menerapkan 4 algoritma yang berbeda (3 di antaranya diadaptasi untuk teka-teki warna). Yang tercepat ternyata adalah algoritma BguSolver, dinamai dari sumber aslinya . Ini adalah metode yang sangat efektif dan hampir standar untuk menyelesaikan string nonogram menggunakan pemrograman dinamis. Pseudocode metode ini dapat ditemukan, misalnya, dalam artikel ini .

  
  

• ( propagasi ) kami menempatkan semua baris dan kolom dalam antrian, melewatinya dengan pemecah linear, ketika kami menerima informasi baru ketika memecahkan baris (kolom), kami memperbarui antrian, masing-masing, dengan kolom baru (baris). Lanjutkan sampai saluran kosong.

  
  
  Contoh dan kode

  Kami mengambil tugas selanjutnya untuk menyelesaikan dari antrian. Biarkan itu menjadi string kosong (tidak terselesaikan) dengan panjang 7 (kami menyatakan sebagai ??????? ) dengan deskripsi dari blok [2, 3] . Pemecah linear akan menghasilkan string yang sebagian diselesaikan ?X??XX? di mana X adalah sel yang diisi. Saat memperbarui baris, kita melihat bahwa kolom dengan angka 1, 4, 5 telah berubah (pengindeksan dimulai pada 0). Ini berarti bahwa informasi baru telah muncul di kolom yang ditunjukkan dan mereka dapat dikembalikan ke pemecah "linear". Kami menempatkan kolom-kolom ini dalam antrian tugas-tugas dengan prioritas lebih tinggi (untuk memberikannya kepada pemecah linear berikutnya).

  
  

   def propagation(board): line_jobs = PriorityDict() for row_index in range(board.height): new_job = (False, row_index) line_jobs[new_job] = 0 for column_index in range(board.width): new_job = (True, column_index) line_jobs[new_job] = 0 for (is_column, index), priority in line_jobs.sorted_iter(): new_jobs = solve_and_update(board, index, is_column) for new_job in new_jobs: # upgrade priority new_priority = priority - 1 line_jobs[new_job] = new_priority def solve_and_update(board, index, is_column): if is_column: row_desc = board.columns_descriptions[index] row = tuple(board.get_column(index)) else: row_desc = board.rows_descriptions[index] row = tuple(board.get_row(index)) updated = line_solver(row_desc, row) if row != updated: for i, (pre, post) in enumerate(zip(row, updated)): if _is_pixel_updated(pre, post): yield (not is_column, i) if is_column: board.set_column(index, updated) else: board.set_row(index, updated) 

  
  
  
  

• ( menyelidiki ) untuk setiap sel yang belum terselesaikan, kami memilah-milah semua pilihan warna dan mencoba menyebarkan dengan informasi baru ini. Jika kita mendapat kontradiksi, kita membuang warna ini dari opsi warna untuk sel dan mencoba mengambil manfaat darinya lagi menggunakan propagasi. Jika diselesaikan hingga akhir, kami menambahkan solusi ke daftar solusi, tetapi terus bereksperimen dengan warna lain (mungkin ada beberapa solusi). Jika kita sampai pada situasi di mana tidak mungkin untuk diselesaikan lebih lanjut, kita cukup mengabaikan dan mengulangi prosedur dengan warna / sel yang berbeda.

  
  
  Kode

  Pengembalian Benar jika kontradiksi diterima sebagai hasil dari sampel.

  
  

   def probe(self, cell_state): board = self.board pos, assumption = cell_state.position, cell_state.color # already solved if board.is_cell_solved(pos): return False if assumption not in board.cell_colors(pos): LOG.warning("The probe is useless: color '%s' already unset", assumption) return False save = board.make_snapshot() try: board.set_color(cell_state) propagation( board, row_indexes=(cell_state.row_index,), column_indexes=(cell_state.column_index,)) except NonogramError: LOG.debug('Contradiction', exc_info=True) # rollback solved cells board.restore(save) else: if board.is_solved_full: self._add_solution() board.restore(save) return False LOG.info('Found contradiction at (%i, %i)', *pos) try: board.unset_color(cell_state) except ValueError as ex: raise NonogramError(str(ex)) propagation( board, row_indexes=(pos.row_index,), column_indexes=(pos.column_index,)) return True 

  
  
  
  

• ( mundur ) jika selama penyelidikan Anda tidak mengabaikan teka-teki yang sebagian terpecahkan, tetapi terus menggunakan prosedur yang sama secara rekursif, kami mendapatkan pengulangan (dengan kata lain, berjalan lengkap ke kedalaman pohon keputusan potensial). Di sini, peran besar mulai dimainkan, sel mana yang akan dipilih sebagai perpanjangan selanjutnya dari solusi potensial. Penelitian yang baik tentang topik ini ada di publikasi ini .

  
  
  Kode

  Mundur dengan saya cukup berantakan, tetapi dua fungsi ini menggambarkan kira-kira apa yang terjadi selama pencarian rekursif

  
  

   def search(self, search_directions, path=()): """ Return False if the given path is a dead end (no solutions can be found) """ board = self.board depth = len(path) save = board.make_snapshot() try: while search_directions: state = search_directions.popleft() assumption, pos = state.color, state.position cell_colors = board.cell_colors(pos) if assumption not in cell_colors: LOG.warning("The assumption '%s' is already expired. " "Possible colors for %s are %s", assumption, pos, cell_colors) continue if len(cell_colors) == 1: LOG.warning('Only one color for cell %r left: %s. Solve it unconditionally', pos, assumption) try: self._solve_without_search() except NonogramError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The path %s is invalid", assumption, pos, path) return False if board.is_solved_full: self._add_solution() LOG.warning( "The only color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True continue rate = board.solution_rate guess_save = board.make_snapshot() try: LOG.warning('Trying state: %s (depth=%d, rate=%.4f, previous=%s)', state, depth, rate, path) success = self._try_state(state, path) finally: board.restore(guess_save) if not success: try: LOG.warning( "Unset the color %s for cell '%s'. Solve it unconditionally", assumption, pos) board.unset_color(state) self._solve_without_search() except ValueError: LOG.warning( "The last possible color '%s' for the cell '%s' " "lead to the contradiction. " "The whole branch (depth=%d) is invalid. ", assumption, pos, depth) return False if board.is_solved_full: self._add_solution() LOG.warning( "The negation of color '%s' for the cell '%s' lead to full solution. " "No need to traverse the path %s anymore", assumption, pos, path) return True finally: # do not restore the solved cells on a root path - they are really solved! if path: board.restore(save) return True def _try_state(self, state, path): board = self.board full_path = path + (state,) probe_jobs = self._get_all_unsolved_jobs(board) try: # update with more prioritized cells for new_job, priority in self._set_guess(state): probe_jobs[new_job] = priority __, best_candidates = self._solve_jobs(probe_jobs) except NonogramError as ex: LOG.warning('Dead end found (%s): %s', full_path[-1], str(ex)) return False rate = board.solution_rate LOG.info('Reached rate %.4f on %s path', rate, full_path) if rate == 1: return True cells_left = round((1 - rate) * board.width * board.height) LOG.info('Unsolved cells left: %d', cells_left) if best_candidates: return self.search(best_candidates, path=full_path) return True 

  
  
  
  

Jadi, kami mulai memecahkan teka-teki silang kami dari tingkat kedua (yang pertama hanya cocok untuk kasus degenerasi, ketika di seluruh teka-teki silang hanya ada satu baris atau kolom) dan secara bertahap naik ke atas tingkat. Seperti yang Anda tebak, setiap level menyebabkan level yang mendasari beberapa kali, jadi untuk solusi yang efektif sangat penting untuk memiliki level pertama dan kedua yang cepat, yang dapat dipanggil jutaan kali untuk teka-teki kompleks.

Pada tahap ini, ternyata (agak diharapkan) bahwa python sama sekali bukan alat yang cocok untuk kinerja maksimum dalam tugas intensif CPU: semua perhitungan di dalamnya sangat tidak efisien dibandingkan dengan bahasa tingkat rendah. Sebagai contoh, pemecah BGU yang paling algoritmik (di Jawa), menurut hasil pengukuran, ternyata 7-17 (kadang-kadang hingga 27) kali lebih cepat pada berbagai tugas.

         pynogram_my BGU_my speedup
 Dancer 0,976 0,141 6,921986      
 Cat 1.064 0.110 9.672727      
 Skid 1.084 0.101 10.732673     
 Bucks 1,116 0,118 9,457627      
 Edge 1,208 0,094 12,851064     
 Asap 1.464 0.120 12.200000     
 Simpul 1,332 0,140 9,514286      
 Ayunkan 1,784 0,138 12,927536     
 Ibu 2.108 0,147 14,340136     
 DiCap 2.076 0.176 11.795455     
 Tragis 2,368 0,265 8,935849      
 Merka 2.084 0.196 10.632653     
 Petro 2.948 0.219 13.461187     
 M&M 3.588 0,375 9,568000      
 Ditandatangani 4.068 0,242 16,809917     
 Cahaya 3,848 0,488 7,885246      
 Selamanya 111.000 13.570 8.179808  
 Center 5.700 0.327 17.431193     
 Panas 3.150 0.278 11.330935     
 Karate 2.500 0,219 11,415525     
 9-Dom 510.000 70.416 7.242672      
 Bendera 149.000 5.628 26.474769     
 Singa 71.000 2.895 24.525043     
 Marley 12.108 4.405 2.748695      
 Hal 321.000 46.166 6.953169      
 Inf alam 433.138 inf     
 Tambah inf NaN      
 Gettys inf inf NaN      

Dan ini sudah setelah saya mulai menggunakan PyPy, dan pada CPython standar waktu perhitungan lebih lama dari pada PyPy 4-5 kali! Kita dapat mengatakan bahwa kinerja pemecah Java yang serupa ternyata 28-85 kali lebih tinggi daripada kode CPython.

Upaya untuk meningkatkan kinerja solver saya menggunakan profil (cProfile, SnakeViz, line_profiler) menyebabkan beberapa percepatan, tetapi tentu saja mereka tidak memberikan hasil yang luar biasa.

Ringkasan :

+ pemecah dapat menyelesaikan semua teka-teki dari situs https://webpbn.com , http://nonograms.org dan formatnya sendiri (berbasis-berbasis)

+ memecahkan nonograms hitam-putih dan warna dengan jumlah warna apa pun (jumlah warna maksimum yang dipenuhi adalah 10)

+ memecahkan teka-teki dengan ukuran blok yang hilang (blotted). Contoh dari teka-teki seperti itu .

+ dapat membuat teka-teki ke konsol / ke kutukan / jendela di browser (saat memasang opsi pynogram-web tambahan). Untuk semua mode, melihat progres solusi secara real time didukung.

- perhitungan lambat (dibandingkan dengan implementasi yang dijelaskan dalam artikel-perbandingan pemecah, lihat tabel ).

- backtracking yang tidak efisien: beberapa puzzle dapat dipecahkan berjam-jam (ketika pohon keputusan sangat besar).

Karat

Pada awal tahun, saya mulai belajar Rust. Saya mulai, seperti biasa, dengan The Book , belajar tentang WASM, mempelajari tutorial yang diajukan . Namun, saya menginginkan beberapa tugas nyata di mana Anda dapat terlibat dalam kekuatan bahasa (terutama kinerja supernya), dan bukan beberapa contoh yang ditemukan oleh seseorang. Jadi saya kembali ke nonogram. Tapi sekarang saya sudah memiliki versi yang berfungsi dari semua algoritma di Python, diserahkan kepada "hanya" menulis ulang.

Berita baik itu menantikan saya dari awal: ternyata Rust, dengan sistem tipenya, dengan sempurna menggambarkan struktur data untuk tugas saya. Misalnya, salah satu korespondensi dasar BinaryColor + BinaryBlock / MultiColor + ColoredBlock memungkinkan Anda untuk memisahkan non -hitam-putih dan warna secara permanen. Jika di suatu tempat dalam kode kami mencoba untuk menyelesaikan string berwarna menggunakan blok deskripsi biner biasa, kami mendapatkan kesalahan kompilasi tentang tipe mismatch.

 pub trait Color { fn blank() -> Self; fn is_solved(&self) -> bool; fn solution_rate(&self) -> f64; fn is_updated_with(&self, new: &Self) -> Result<bool, String>; fn variants(&self) -> Vec<Self>; fn as_color_id(&self) -> Option<ColorId>; fn from_color_ids(ids: &[ColorId]) -> Self; } pub trait Block { type Color: Color; fn from_str_and_color(s: &str, color: Option<ColorId>) -> Self { let size = s.parse::<usize>().expect("Non-integer block size given"); Self::from_size_and_color(size, color) } fn from_size_and_color(size: usize, color: Option<ColorId>) -> Self; fn size(&self) -> usize; fn color(&self) -> Self::Color; } #[derive(Debug, PartialEq, Eq, Hash, Clone)] pub struct Description<T: Block> where T: Block, { pub vec: Vec<T>, } // for black-and-white puzzles #[derive(Debug, PartialEq, Eq, Hash, Copy, Clone, PartialOrd)] pub enum BinaryColor { Undefined, White, Black, BlackOrWhite, } impl Color for BinaryColor { // omitted } #[derive(Debug, PartialEq, Eq, Hash, Default, Clone)] pub struct BinaryBlock(pub usize); impl Block for BinaryBlock { type Color = BinaryColor; // omitted } // for multicolor puzzles #[derive(Debug, PartialEq, Eq, Hash, Default, Copy, Clone, PartialOrd, Ord)] pub struct MultiColor(pub ColorId); impl Color for MultiColor { // omitted } #[derive(Debug, PartialEq, Eq, Hash, Default, Clone)] pub struct ColoredBlock { size: usize, color: ColorId, } impl Block for ColoredBlock { type Color = MultiColor; // omitted } 

Saat porting kode, beberapa titik dengan jelas menunjukkan bahwa bahasa yang diketik secara statis seperti Rust (well, atau, misalnya, C ++) lebih cocok untuk tugas ini. Lebih tepatnya, generik dan sifat menggambarkan domain lebih baik daripada hierarki kelas. Jadi dalam kode Python, saya punya dua kelas untuk BguSolver linear, BguSolver dan BguColoredSolver yang masing-masing memecahkan garis hitam-putih dan garis warna. Dalam kode Rust, saya masih memiliki satu-satunya struct DynamicSolver<B: Block, S = <B as Block>::Color> generik struct DynamicSolver<B: Block, S = <B as Block>::Color> struktur, yang dapat menyelesaikan kedua jenis tugas, tergantung pada jenis yang diteruskan selama pembuatan ( DynamicSolver<BinaryBlock>, DynamicSolver<ColoredBlock> ). Ini, tentu saja, tidak berarti bahwa sesuatu yang serupa tidak dapat dilakukan dengan Python, hanya dalam sistem tipe Rust jelas menunjukkan kepada saya bahwa jika Anda tidak pergi dengan cara ini, Anda harus menulis satu ton kode berulang.

Selain itu, siapa pun yang mencoba menulis di Rust, tidak diragukan lagi memperhatikan efek "kepercayaan" pada kompiler, ketika proses penulisan kode turun ke algoritma pseudo-meta berikut:

 write_initial_code
 while (compiler_hints = $ (cek kargo))! = 0;  lakukan
     fix_errors (compiler_hints)
 akhir

Ketika kompiler berhenti mengeluarkan kesalahan dan peringatan, kode Anda akan konsisten dengan sistem tipe dan pemeriksa pinjaman dan Anda akan memberi peringatan sebelumnya tentang adanya bug potensial (tentu saja, tergantung pada desain tipe data yang cermat).

Saya akan memberikan beberapa contoh fungsi yang menunjukkan betapa ringkasnya kode Rust (dibandingkan dengan rekan-rekan Python).

 def unsolved_neighbours(self, position): for pos in self.neighbours(position): if not self.is_cell_solved(*pos): yield pos 

 fn unsolved_neighbours(&self, point: &Point) -> impl Iterator<Item = Point> + '_ { self.neighbours(&point) .into_iter() .filter(move |n| !self.cell(n).is_solved()) } 

             1 2 3 4 5 6 7 8 9 
             _ _ _ _ _ _ _ _ _ _
      2 3 1 | _ | _ | _ | _ | _ | _ | _ | _ | 
               ^ ^ ^
               |  |  |
 akhir 1 blok |  |  | 
 akhir blok 2 -------- |
 akhir blok 3 ------------

 @expand_generator def partial_sums(blocks): if not blocks: return sum_so_far = blocks[0] yield sum_so_far for block in blocks[1:]: sum_so_far += block + 1 yield sum_so_far 

 fn partial_sums(desc: &[Self]) -> Vec<usize> { desc.iter() .scan(None, |prev, block| { let current = if let Some(ref prev_size) = prev { prev_size + block.0 + 1 } else { block.0 }; *prev = Some(current); *prev }) .collect() } 

Saat porting, saya membuat beberapa perubahan

• core solver (algoritma) mengalami perubahan kecil (terutama untuk mendukung tipe generik untuk sel dan blok)
• meninggalkan satu-satunya algoritma (tercepat) untuk pemecah linear
• alih-alih format ini, memperkenalkan format TOML yang sedikit dimodifikasi
• tidak menambahkan dukungan untuk teka-teki silang blotted, karena, sebenarnya, ini adalah kelas tugas yang berbeda

• meninggalkan satu-satunya cara untuk output - hanya untuk konsol, tetapi sekarang sel-sel berwarna di konsol ditarik benar-benar berwarna (berkat peti ini )

  
  
  seperti itu

  

  
  
  
  

Alat yang berguna

• Clippy adalah penganalisa statis standar yang kadang-kadang bahkan dapat memberikan tips sedikit meningkatkan kinerja kode.
• valgrind adalah alat untuk analisis aplikasi dinamis. Saya menggunakannya sebagai profiler untuk mencari botneks ( valrgind --tool=callgrind ) dan khususnya bagian kode yang valrgind --tool=massif memori ( valrgind --tool=massif ). Kiat: atur [profile.release] debug = true ke Cargo.toml sebelum memulai profiler. Ini akan meninggalkan karakter debug di executable.
• kcachegrind untuk melihat file callgrind. Alat yang sangat berguna untuk menemukan tempat yang paling bermasalah dalam hal kinerja.

Performa

Itu untuk apa penulisan ulang pada Rust dimulai. Kami mengambil teka-teki silang dari tabel perbandingan yang telah disebutkan dan menjalankannya melalui pemecah terbaik yang dijelaskan dalam artikel asli. Hasil dan deskripsi jalan di sini . Kami mengambil file yang dihasilkan dan membangun beberapa grafik di atasnya. Karena waktu solusi bervariasi dari milidetik hingga puluhan menit, grafik dibuat dengan skala logaritmik.

 import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline # strip the spaces df = pd.read_csv('perf.csv', skipinitialspace=True) df.columns = df.columns.str.strip() df['name'] = df['name'].str.strip() # convert to numeric df = df.replace('\+\ *', np.inf, regex=True) ALL_SOLVERS = list(df.columns[3:]) df.loc[:,ALL_SOLVERS] = df.loc[:,ALL_SOLVERS].apply(pd.to_numeric) # it cannot be a total zero df = df.replace(0, 0.001) #df.set_index('name', inplace=True) SURVEY_SOLVERS = [s for s in ALL_SOLVERS if not s.endswith('_my')] MY_MACHINE_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] in SURVEY_SOLVERS] MY_SOLVERS = [s for s in ALL_SOLVERS if s.endswith('_my') and s[:-3] not in SURVEY_SOLVERS] bar_width = 0.17 df_compare = df.replace(np.inf, 10000, regex=True) plt.rcParams.update({'font.size': 20}) def compare(first, others): bars = [first] + list(others) index = np.arange(len(df)) fig, ax = plt.subplots(figsize=(30,10)) df_compare.sort_values(first, inplace=True) for i, column in enumerate(bars): ax.bar(index + bar_width*i, df_compare[column], bar_width, label=column[:-3]) ax.set_xlabel("puzzles") ax.set_ylabel("Time, s (log)") ax.set_title("Compare '{}' with others (lower is better)".format(first[:-3])) ax.set_xticks(index + bar_width / 2) ax.set_xticklabels("#" + df_compare['ID'].astype(str) + ": " + df_compare['name'].astype(str)) ax.legend() plt.yscale('log') plt.xticks(rotation=90) plt.show() fig.savefig(first[:-3] + '.png', bbox_inches='tight') for my in MY_SOLVERS: compare(my, MY_MACHINE_SOLVERS) compare(MY_SOLVERS[0], MY_SOLVERS[1:]) 

pemecah python

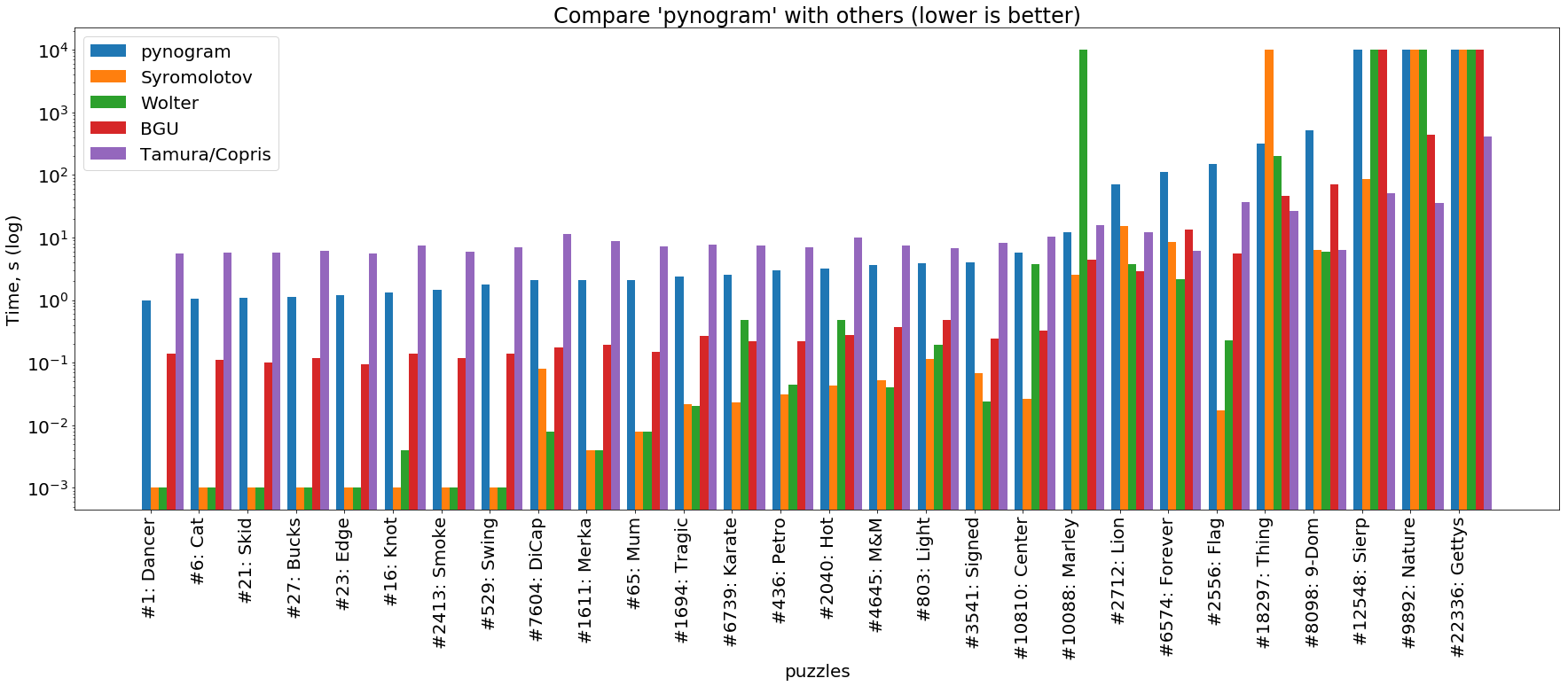
( gambar dapat diklik )

Kita melihat bahwa pynogram di sini lebih lambat dari semua pemecah yang disajikan. Satu-satunya pengecualian untuk aturan ini adalah pemecah Tamura / Copris berdasarkan SAT, yang memecahkan teka-teki paling sederhana (bagian kiri grafik) lebih lama dari kita. Namun, ini adalah fitur SAT-solver: mereka dirancang untuk teka-teki silang super kompleks di mana solver biasa terjebak dalam backtracking untuk waktu yang lama. Ini terlihat jelas di sisi kanan grafik, di mana Tamura / Copris memecahkan teka-teki paling sulit puluhan dan ratusan kali lebih cepat daripada yang lainnya.

pemecah karat

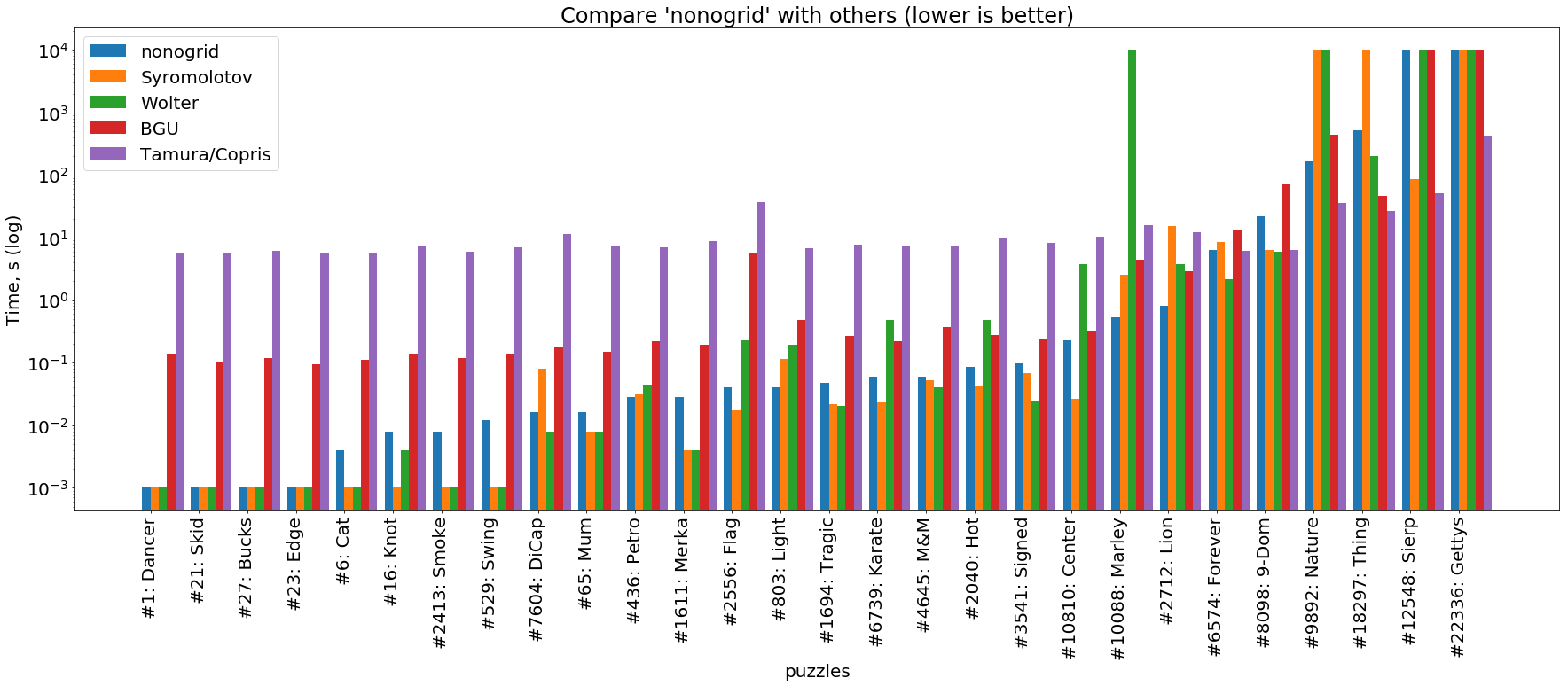
( gambar dapat diklik )

Grafik ini menunjukkan bahwa nonogrid pada tugas-tugas sederhana juga mengatasi atau sedikit lebih buruk daripada pemecah kinerja tinggi yang ditulis dalam C dan C ++ ( Wolter dan Syromolotov ). Dengan kerumitan tugas, pemecah kami kira-kira mengulangi lintasan pemecah BGU (Jawa), tetapi hampir selalu di depannya dengan sekitar urutan besarnya. Pada tugas yang paling sulit, Tamura / Copris selalu di depan semua orang.

karat vs python

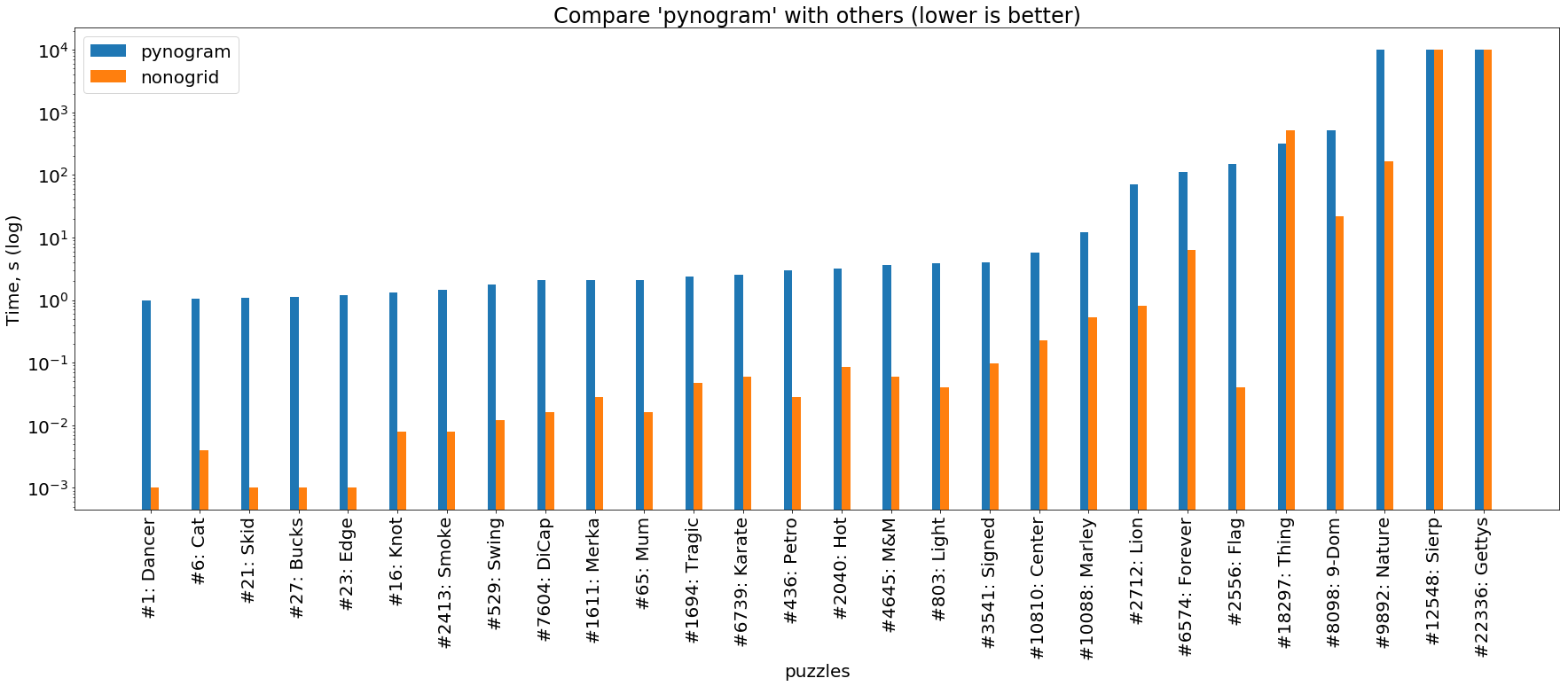
( gambar dapat diklik )

Dan akhirnya, perbandingan dua pemecah kami yang dijelaskan di sini. Dapat dilihat bahwa solver Rust hampir selalu adalah 1-3 urutan besarnya di depan solver python.

Ringkasan :

+ solver dapat menyelesaikan semua teka-teki dari situs https://webpbn.com (kecuali blotted - dengan ukuran blok yang sebagian tersembunyi), http://nonograms.org dan formatnya sendiri (berbasis TOML)

+ Memecahkan nonograms hitam dan putih dan warna dengan sejumlah warna

+ dapat membuat teka-teki ke konsol (warna c webpbn.com menarik warna asli)

+ bekerja cepat (dibandingkan dengan implementasi yang dijelaskan dalam artikel-perbandingan pemecah, lihat tabel).

- Mundur tetap tidak efektif, seperti dalam solusi Python: beberapa teka-teki (misalnya , 20x20 tidak berbahaya ) dapat diselesaikan selama berjam-jam (ketika pohon keputusan sangat besar). Mungkin alih-alih mundur, ada baiknya menggunakan pemecah SAT yang telah disebutkan pada hub Benar, satu-satunya pemecah SAT yang saya temukan di Rust pada pandangan pertama tampaknya belum selesai dan ditinggalkan.

Perakitan web

Jadi, menulis ulang kode di Rust telah terbayar: pemecah masalah menjadi jauh lebih cepat. Namun, Rust menawarkan kepada kami fitur keren lainnya: kompilasi di WebAssembly dan kemampuan untuk menjalankan kode Anda langsung di browser.

Untuk mengimplementasikan fitur ini, ada alat khusus untuk Rust yang menyediakan pengikat yang diperlukan dan menghasilkan pelat ketel untuk Anda tanpa kesulitan menjalankan fungsi Rust dalam kode JS - paket wasm ini (+ wasm-bindgen ). Sebagian besar pekerjaan dengan itu dan alat penting lainnya sudah dijelaskan dalam tutorial Karat dan WebAssembly . Namun, ada beberapa poin yang harus saya pikirkan sendiri:

• saat membaca, itu menciptakan perasaan bahwa tutorial ini terutama ditulis untuk pengembang JS yang ingin mempercepat kodenya dengan Rust. Ya, atau setidaknya untuk seseorang yang terbiasa dengan npm . Bagi saya, sebagai orang yang jauh dari ujung depan, itu mengejutkan untuk menemukan bahwa bahkan contoh standar dari buku tidak ingin bekerja dengan server web pihak ketiga yang berbeda dari npm run start .

  
  

  Untungnya, wasm-pack memiliki mode yang memungkinkan Anda untuk menghasilkan kode JS biasa (yang bukan modul npm). wasm-pack build --target no-modules --no-typescript pada output hanya akan menghasilkan dua file: project-name.wasm - biner dari kode Rust yang dikompilasi ke dalam WebAssembly dan project-name.js . File terakhir dapat ditambahkan ke halaman HTML apa saja <script src="project-name.js"></script> dan gunakan fungsi WASM tanpa mengganggu npm, webpack, ES6, modul, dan kesenangan lain dari pengembang JS modern. Mode no-modules ideal untuk pengembang non-front-end selama pengembangan aplikasi WASM, serta untuk contoh dan demo, karena tidak memerlukan infrastruktur front-end tambahan.

  
  

• WebAssembly baik untuk tugas-tugas yang terlalu berat untuk JavaScript. Pertama-tama, ini adalah tugas yang melakukan banyak perhitungan. Dan jika demikian, tugas seperti itu dapat dilakukan untuk waktu yang lama bahkan dengan WebAssembly dan dengan demikian melanggar prinsip asinkron dari web modern. Saya berbicara tentang semua jenis Peringatan: Skrip tidak responsif yang kebetulan saya amati ketika pemecah saya bekerja. Untuk mengatasi masalah ini, Anda dapat menggunakan mekanisme pekerja Web . Dalam kasus ini, skema untuk bekerja dengan fungsi WASM "berat" mungkin terlihat seperti ini:

  
  
  1. dari skrip utama untuk suatu acara (misalnya, mengklik tombol) mengirim pesan ke pekerja dengan tugas meluncurkan fungsi yang berat.
  2. , .
  3. - ()
  
  

WASM- JS, WASM . - ( ), HashMap , . ( JS) , / .

, Mutex , thread-safe. smart- . thread-safe Rc Arc RefCell RwLock . : 30%. --features=threaded thread-safe , WASM-.

6574 8098 ( 10 ):

, - 40..70% , , (32..37%) thread-safe ( cargo build --release --features=threaded ).

Firefox 67.0 Chromium 74.0.

WASM- ( ). https://webpbn.com/ http://www.nonograms.org/

TODO

• "" /, / .

  
  

• , . "" , , . .

  
  

• ( , 3600 ). WASM , ( , (!) , , WASM). , , - , nonogrid .

  
  

• . : , , WASM . , ( ) , JS , .

  
  

• JS. backtrace, .

  
  

• ( TOML- )

  
  

Ringkasan

• , (, , etc).

  
  

• Rust 1-3 PyPy 1.5-2 ( ).

  
  

• Python Rust , Python (, , comprehensions), Rust-.

  
  

• Rust WebAssembly . Rust , WASM, ( 1.5 ).

  
  

1. The 'pbnsolve' Paint-by-Number Puzzle Solver by Jan Wolter and the survey
2. The BGU Nonograms Project
3. Solving Nonograms by combining relaxations
4. An Efficient Approach to Solving Nonograms
6. Color and black and white Japanese crosswords on-line
8. 'Nonolib' library by Dr. Steven Simpson
9. Rust and WebAssembly