Mainkan Tetris in AR

Terpikir oleh saya suatu gagasan aneh bahwa rumah itu bisa menjadi platform yang baik untuk bermain Tetris. Tidak jauh dari saya hanya ada satu bangunan yang cocok untuk ini. Hasilnya bisa dilihat di video:


Proyek ini dilaksanakan pada tingkat yang cukup rendah, tanpa menggunakan solusi yang sudah jadi.

Kode sumber

Paling sering mereka menggunakan 2 opsi untuk mengimplementasikan augmented reality:

• tanpa penanda, mis. posisi kamera ditentukan oleh pergerakan titik-titik utama dari aliran videonya;
• gambar sebagai penanda relatif terhadap posisi kamera.

Implementasi ini tidak memerlukan persiapan khusus atau kondisi khusus.

Ada opsi implementasi lain - untuk mengenali objek tertentu dan menggunakannya sebagai penanda. Ini membutuhkan setidaknya kehadirannya, tetapi memungkinkan untuk mengontrolnya secara visual. Salah satu metode pengenalan tersebut adalah deteksi objek dengan tepi. Ini memiliki keterbatasan - objek penanda harus memiliki tepi yang jelas, mis. objek kemungkinan besar harus padat.

Atau ujung-ujungnya harus digambarkan dengan jelas, seperti penerangan gedung ini:



Dapat dilihat bahwa lampu latar dapat dengan mudah dipisahkan dalam gambar dan digunakan untuk deteksi.

Implementasi

Pada Qt. Kerangka kerja ini memungkinkan Anda untuk bekerja pada platform yang berbeda dan pada saat yang sama dalam C ++. Karena kinerja penting bagi kami, pro sepertinya pilihan yang jelas.

Meskipun Qt tidak bekerja dengan baik dengan android (peluncuran panjang, debugging dinonaktifkan), tetapi ini semua diratakan oleh kemampuan untuk debug algoritma pada desktop.

Grafik tiga dimensi divisualisasikan pada OpenGL mentah yang disematkan pada Qt.

Bekerja dengan kamera dilakukan melalui Qt. Video direkam untuk debugging, dan cukup nyaman untuk mengganti aliran video kamera dengan aliran video dari file.

Output dilakukan melalui alat qml. Untuk berteman qml dan OpenGL bukan tanpa masalah, tapi kami tidak akan memikirkan hal ini.

Untuk pemrosesan gambar, pustaka OpenCV terhubung.

Algoritma Pelacakan

Sekarang mari kita beralih ke bagian yang paling menarik - algoritma untuk melacak objek di sepanjang tepinya.
Dan mulailah dengan menyorot bagian tepi pada gambar. Semua tepi dalam kasus kami memiliki bentuk garis lurus, jadi pikiran pertama yang terlintas dalam pikiran adalah menggunakan detektor garis. Transformasi Hough dapat digunakan sebagai detektor garis. Namun, cara ini menurut saya tidak terlalu benar, karena transformasi Hough cukup mahal, dan detektor ini sangat tidak dapat diandalkan (ini subjektif, mungkin semuanya tergantung pada tugas).
Sebagai gantinya, mari kita pergi dengan cara yang berbeda, lebih umum. Kami tidak akan mempertimbangkan bahwa garis kami lurus, tetapi kami akan bekerja hanya pada gambar biner. Kehadiran tepi akan dikodekan ke dalam gambar biner. Yaitu piksel dengan nilai nol berarti ada tepi di tempat ini, nilai piksel lebih besar dari nol - tidak ada tepi. Gambar seperti itu dapat diperoleh dengan menggunakan detektor batas Canny atau menggunakan transformasi ambang batas sederhana. Algoritma ini dapat ditemukan di OpenCV.

OpenCV juga memiliki fungsi lain yang berguna bagi kita sekarang - distanceTransform , yang mengambil gambar biner pada input dan memberikan gambar pada output, dalam piksel yang jaraknya ke nol piksel terdekat dikodekan.

Sekarang anggaplah kita sudah memiliki perkiraan baik pertama tentang di mana model kita seharusnya berada. Selanjutnya, kami menggambarkan fungsi kesalahan, yang menggambarkan seberapa jauh tepi perkiraan kami tidak sesuai dengan tepi pada gambar yang dihasilkan. Menggunakan gambar dari distanceTransform kita sudah dapat melakukan ini. Dan kemudian kita menjalankan algoritma optimasi fungsi, hanya mengubah perkiraan posisi objek di ruang angkasa. Akibatnya, perkiraan kami harus cukup akurat menggambarkan posisi sebenarnya dari objek.
Hasilnya, algoritme dapat dibagi menjadi dua tahap:

1. Preprocessing gambar - binarisasi, pemfilteran, dan penggunaan fungsi distanceTransfrom.
2. Pelacakan - optimalisasi fungsi kesalahan.

Pra-pemrosesan gambar

Pada titik ini, Anda perlu menyorot tepi pada gambar. Anda dapat menggunakan detektor batas Canny, tetapi dalam kasus kami, konversi ambang biasa atau versi adaptifnya bekerja lebih baik (di OpenCV, ini adalah fungsi ambang batas atau fungsi adaptif). Jelas bahwa akan ada noise pada gambar seperti itu, sehingga penyaringan diperlukan. Mari kita lakukan sebagai berikut - pilih kontur menggunakan fungsi OpenCV findCountour dan hapus segmen yang terlalu kecil atau tidak cukup seperti garis.

Hasil pemrosesan dapat dilihat pada gambar:



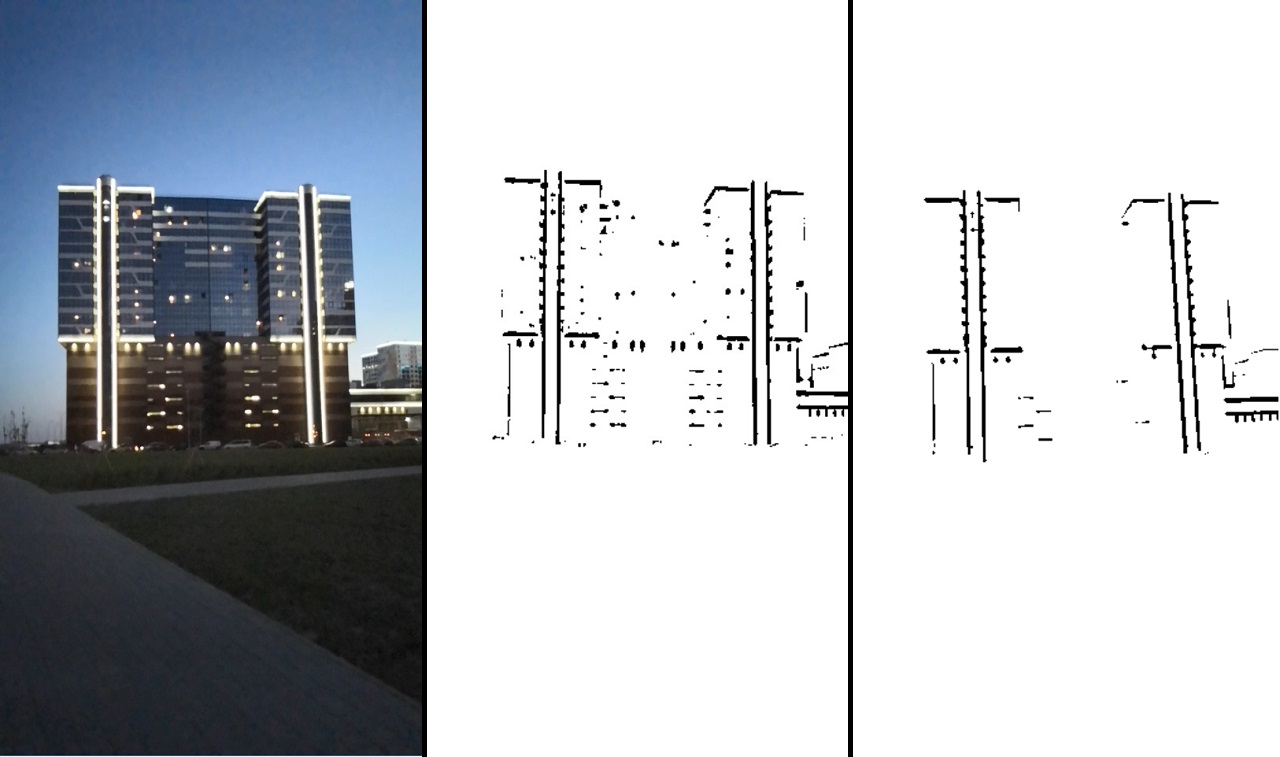
Secara konsisten: gambar asli -> setelah transformasi ambang -> setelah pemfilteran.

Gambar ini sudah cukup jelas memberi tahu kita di mana ada tepi kanan dan di mana tidak. Setelah itu, kami menggunakan fungsi distanceTransform, dan sebagai hasilnya, kami akan memiliki informasi tentang seberapa jauh setiap titik dari tepi. Gambar yang dihasilkan dilambangkan sebagai .

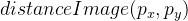
Ini adalah tampilannya jika dinormalisasi dan divisualisasikan:



Selanjutnya, kita akan membutuhkan beberapa alat matematika.

Algoritma Pengoptimalan Fungsi

Optimalisasi fungsi adalah tugas menemukan minimum suatu fungsi.

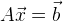
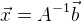
Jika kita berurusan dengan sistem persamaan linear, maka menemukan minimum adalah cukup sederhana. Bayangkan sistem persamaan dalam bentuk matriks: , maka solusi kami: . Jika kita memiliki sistem persamaan yang terlalu ditentukan, maka kita dapat menggunakan metode kuadrat terkecil : .

Jika fungsi kita non-linear, maka tugasnya menjadi lebih rumit. Untuk menemukan minimum, Anda dapat menggunakan algoritma Gauss-Newton . Algoritma bekerja sebagai berikut:

1. Diasumsikan bahwa kita sudah memiliki beberapa perkiraan awal dari solusi yang kita akan memperbaiki berulang.
2. Dengan menggunakan ekspansi Taylor, kita dapat memperkirakan fungsi nonlinear linear pada titik perkiraan saat ini. Kami memecahkan sistem persamaan linear yang dihasilkan dengan metode kuadrat terkecil, memperoleh 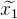. Akibatnya, solusi yang dihasilkan tidak akan menjadi solusi, tetapi akan lebih dekat daripada perkiraan saat ini.
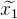3. Ganti perkiraan saat ini menerima keputusan dan lanjutkan ke langkah 2. Jadi ulangi sampai selisihnya dan tidak akan kurang dari nilai tertentu.

Mari kita menganalisis algoritma lebih terinci.

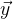
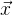
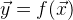
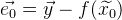
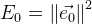
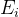
Biarkan - fungsi kerja, - vektor nilai fungsi yang sebelumnya diketahui. Dengan solusi sempurna untuk persamaan pernyataan berikut ini benar . Tapi kami hanya memiliki perkiraannya saja . Kemudian vektor kesalahan dari pendekatan ini dilambangkan sebagai: . Kesalahan umum dari fungsi ini adalah: . Sekarang menemukan itu dimana akan mencapai minimum, kita akan mendapatkan perkiraan solusi yang lebih baik .
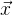
Mulai dari pendekatan kami akan memperkirakannya secara iteratif, mencapai setiap iterasi . Untuk melakukan ini, kita perlu setiap iterasi untuk menghitung matriks Jacobi untuk fungsi untuk perkiraan saat ini, terdiri dari turunan dari fungsi kami:

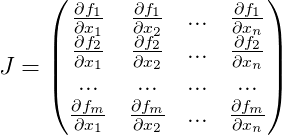
Dan perkiraan berikut diberikan sebagai: .
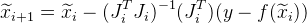
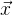
Seringkali tugas dibangun sedemikian rupa sehingga kita memiliki sejumlah besar data yang tidak saling tergantung (hanya dari nilai-nilai saja ) Akibatnya, matriks Jacobi umum sangat jarang. Ada cara untuk mengoptimalkan perhitungan.
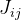
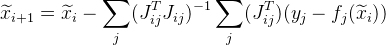
Misalkan fungsi umum dihitung dari seperangkat poin. Dari titik jth kita dapatkan . Alih-alih menghitung matriks Jacobi untuk keseluruhan fungsi, kami menghitung matriks Jacobi khusus untuk dan menyatakannya sebagai: . Maka perkiraan berikut akan diberikan sebagai berikut: . Selain itu, perubahan ini memungkinkan Anda untuk memparalelkan perhitungan.
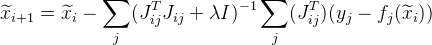
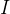
Mungkin saja terjadi nilai berikut akan memberikan kesalahan lebih besar dari . Untuk mengatasi masalah ini, Anda dapat menggunakan modifikasi algoritma - algoritma Levenberg-Marquardt . Nilai tambah ke dalam formula kami: dimana Merupakan matriks satuan. Nilai dipilih sebagai berikut:

• pertama, ia memiliki beberapa nilai yang agak kecil (sedemikian rupa sehingga konvergensi algoritma);
• lalu jika ada kesalahan untuk lebih dari , lalu tambah nilainya dan coba hitung kesalahan untuk lagi.

Semakin non-linear fungsinya semakin besar nilainya . Namun semakin besar nilainya , semakin lambat konvergensi algoritma.

Kami menyelesaikan algoritme kapan berbeda dari cukup kecil dan ambil sebagai solusi.

Algoritma ini cukup universal dan dapat digunakan untuk berbagai tugas.

Model Pelacakan Matematika

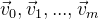
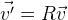
Karena kita berhadapan dengan koordinat dalam ruang, jelas bahwa kita harus dapat memanipulasi koordinat ini. Misalkan kita memiliki beberapa set poin . Dan kita perlu memutarnya di titik dengan nol koordinat. Mungkin cara termudah adalah dengan menggunakan matriks rotasi R , yang menggambarkan rotasi yang diperlukan: . Jika kita perlu menggeser titik, maka tambahkan saja vektor yang diinginkan t : .
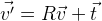
Dengan demikian, Anda dapat mengubah posisi suatu objek dalam ruang secara sewenang-wenang. Ternyata koordinat objek ditentukan oleh matriks tiga dimensi R dan vektor tiga dimensi t , mis. 12 parameter. Selain itu, parameter-parameter ini tidak independen satu sama lain, komponen-komponen dari matriks rotasi saling berhubungan oleh kondisi tertentu. Oleh karena itu, dari sudut pandang penggunaan fungsi-fungsi ini dalam optimasi, parameter ini bukan solusi terbaik. Ada lebih banyak parameter daripada derajat kebebasan, ada hubungan di antara mereka. Ada bentuk rotasi lain - rumus rotasi Rodrigue . Rotasi ini ditentukan oleh tiga parameter, membentuk vektor tiga dimensi.

Vektor yang dinormalisasi adalah sumbu rotasi, dan panjang vektor ini adalah sudut rotasi di sekitar sumbu ini.

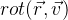
Kami mengatur fungsi rotasi vektor v : menggunakan parameter r dari rumus Rodrigue. Kami mendapatkan formula berikut dari ini: .
Dan pada akhirnya, kita dapat mengatur koordinat posisi objek dengan vektor 6 dimensi:
Kami mendapatkan formula berikut: .

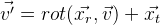
Model kamera lubang jarum

Sekarang kami menggambarkan model matematika sederhana dari kamera yang digunakan dalam proyek:

$$

$$\ vec {p} = \ begin {pmatrix} p_x & p_y \ end {pmatrix} ^ T = cam (\ vec {v}) = \ begin {pmatrix} f_x \ frac {v_x} {v_z} + c_x & f_y \ frac {v_y} {v_z} + c_y \ end {pmatrix} ^ T$$

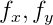
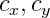
dimana - jarak fokus dalam piksel; - Pusat optik juga dalam piksel. Ini adalah parameter kamera individu, yang disebut parameter intrinsik kamera. Biasanya, parameter ini diketahui sebelumnya. Dalam proyek ini, parameter ini dipilih oleh mata.

Model ini tidak memperhitungkan distorsi lensa kamera ( distorsi ). Misalkan tidak.

Dengan model ini, kami mendapatkan proyeksi pusat, semua titik yang cenderung mengarah ke pusat optik, semakin jauh dari kamera mereka. Dengan demikian kami memperoleh efek dari kereta api penyempitan:



Di ruang angkasa, kamera sejajar dengan sumbu z , bidang gambar sejajar dengan bidang xy . Kami melengkapi model kami dengan kemampuan untuk bergerak di ruang angkasa:

$$

$$\ vec {p} _j = cam (membusuk (\ vec {x} _r, \ vec {v} _j) + \ vec {x} _t)$$

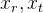
Dengan demikian, kami memperoleh model yang kami dapat dalam bentuk aljabar mensimulasikan proyeksi titik-titik dari dunia luar ke gambar kamera (dari koordinat dunia ke layar). Bagi kami, parameter posisi relatif kamera di ruang angkasa tetap tidak diketahui dalam model ini. . Parameter ini disebut parameter ekstrinsik kamera.

Pelacakan

Sudah diterapkan tanpa alat OpenCV. Pertama, kita perlu mendapatkan fungsi kesalahan untuk solusi perkiraan kami, yang telah dijelaskan di atas. Dan kami akan menulis perhitungannya secara bertahap:

1. Kami memilih tepi model pelacakan yang terlihat berdasarkan parameter perkiraan saat ini.
2. Kami mengubah kumpulan tepi yang dipilih menjadi kumpulan poin yang tetap, untuk menyederhanakan perhitungan. Sebagai contoh, dimungkinkan untuk mengambil jumlah poin ke-n dari setiap sisi, atau (pilihan yang lebih tepat) untuk memilih kuantitas sedemikian sehingga ada jarak tetap dalam piksel di antara titik-titik tersebut. Kami akan menyebutnya titik kontrol (dalam proyek: controlPoint - titik kontrol dan controlPixelDistance - jarak tetap yang sama dalam piksel).
3. Kami memproyeksikan titik kontrol pada gambar. Berkat distanceImage, kita bisa mendapatkan jarak proyeksi titik kontrol ke tepi pada gambar. Dalam kasus yang ideal, semua titik kontrol harus benar-benar terletak di tepi gambar, mis. jarak ke tulang rusuk harus nol. Berdasarkan ini, kami mendapatkan kesalahan untuk titik kontrol tertentu: .
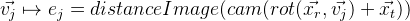4. Kami mendapatkan fungsi kesalahan berikut:

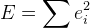
Sekarang tinggal mencari minimum E. Untuk melakukan ini, kami menggunakan algoritma Levenberg-Marquardt yang dijelaskan di atas. Seperti yang telah kita ketahui, algoritme membutuhkan perhitungan matriks Jacobi, yaitu fungsi turunan. Anda dapat menggunakan temuan numerik turunan. Anda juga dapat menggunakan beberapa solusi yang sudah jadi untuk algoritma ini. Namun, dalam proyek ini semuanya ditulis secara manual, jadi saya akan menjelaskan kesimpulan lengkap dari seluruh solusi.

Untuk setiap titik kontrol, kami memperoleh persamaan yang tidak bergantung pada titik lainnya. Telah dijelaskan di atas bahwa dalam hal ini dimungkinkan untuk mempertimbangkan persamaan-persamaan ini secara independen satu sama lain, menghitung matriks Jacobi secara khusus untuk masing-masingnya. Kami akan menganalisisnya secara berurutan, menggunakan aturan diferensiasi fungsi kompleks:



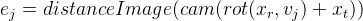
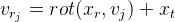
Kami menunjukkan lalu



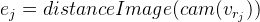
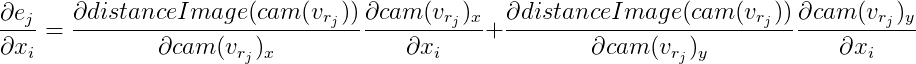
Dari sini:



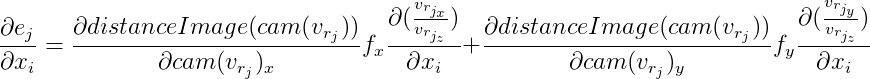
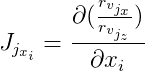
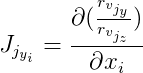
Selanjutnya kami tunjukkan dan lalu:


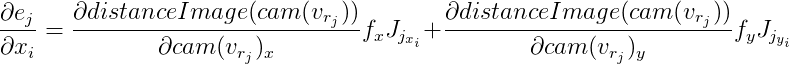
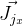
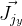
Turunan dari distanceImage adalah angka. Dan untuk menghitung vektor dan Anda perlu menemukan turunannya sesuai dengan rumus rotasi Rodrigue. Saya menemukan Jacobian dengan rumus ini di publikasi “Formula ringkas untuk turunan rotasi 3-D di
koordinat eksponensial »Guillermo Gallego, Anthony Yezzi :

,
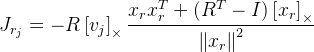
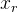
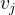
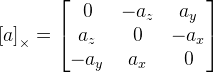
di mana R adalah matriks rotasi yang diperoleh dengan rumus Rodrigue dari vektor rotasi ; - titik kita berputar; Saya adalah matriks identitas; . Seperti yang kita lihat di sini, kita memiliki pembagian dengan panjang vektor rotasi, dan jika vektornya nol, maka rumusnya tidak lagi berfungsi. Ini mungkin disebabkan oleh fakta bahwa pada vektor nol sumbu rotasi tidak ditentukan. Jika vektor rotasi sangat dekat dengan nol, maka kami menggunakan rumus ini: .
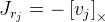
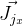
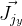
Masih melukis dan (di sini indeks j dihilangkan):


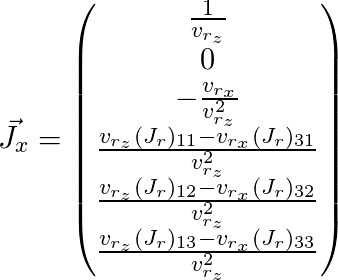
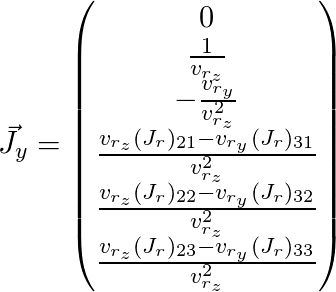
Dengan demikian, kami memperoleh matriks Jacobi untuk titik yang kami butuhkan dan dapat menggunakannya untuk algoritma optimasi yang dijelaskan di atas.

Ada beberapa masalah dengan algoritma ini. Pertama, akurasi. Hasilnya, posisi global kamera sedikit melonjak dari bingkai ke bingkai. Anda bisa memperbaikinya sedikit. Kami memiliki informasi apriori bahwa posisi kamera tidak dapat berubah secara dramatis dari bingkai ke bingkai. Dan kita bisa mengurangi jitter ini dengan menambahkan persamaan tambahan ke fungsi.

Harus diingat bahwa vektor perpindahan t tidak dalam kasus kami mengoordinasikan posisi global kamera. Posisi global adalah titik lokal dengan nol koordinat, sehingga dapat diturunkan sebagai berikut:



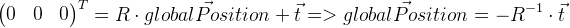
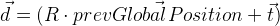
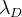
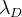
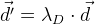
Kami ingat posisi frame sebelumnya di prevGlobalPosition . Sekarang posisi sebelumnya harus mendekati nol, yaitu panjang vektor harus cukup kecil. Yaitu selain nilai-nilai perbedaan lainnya, vektor d juga harus diminimalkan. Untuk menentukan tingkat pengaruh modifikasi ini, kami memperkenalkan nilainya dan kalikan vektor d dengan menambahkan dengan : . Yaitu dalam algoritme pengoptimalan, kami juga meminimalkan vektor d ' . Tentu saja, untuk ini akan perlu untuk menghitung matriks Jacobi untuknya, yang diturunkan dengan cara yang sama seperti yang telah kita peroleh di atas untuk fungsi kesalahan umum.

Masalah kedua dari algoritma adalah bahwa ia bisa macet di minimum lokal. Dalam karya lain, masalah ini diselesaikan menggunakan filter partikel. Dalam kasus kami, opsi ini ternyata, pada prinsipnya, cukup.

Bonus dari pelacakan objek

Mengetahui posisi dan bentuk objek, Anda dapat memanipulasi mereka secara visual, yang saya coba tunjukkan di video. Objek itu terdistorsi menggunakan shader OpenGL. Dengan bantuan model kami, saya memproyeksikan titik objek ke gambar, dan dengan demikian menerima warna titik ini. Kemudian Anda dapat memindahkan titik ini, mendapatkan efek yang menarik - misalnya, morphing. Namun, kita harus ingat bahwa dengan menggeser titik, perlu ada sesuatu yang tetap di tempatnya, jika tidak, inkonsistensi akan menjadi nyata. Selain itu, tergantung pada kualitas pelacakan kami dan bentuk objek, kami akan menerima berbagai efek yang tidak diinginkan karena akumulasi kesalahan, yang masih akan terjadi. Itu hanya perlu diperhitungkan entah bagaimana. Dalam video yang disajikan di atas, saya ingin menunjukkan bahwa augmented reality dapat digunakan sedikit lebih luas dari sekadar memaksakan objek virtual pada gambar.

Ngomong-ngomong, Vuforia SDK mengimplementasikan pelacakan suatu objek berdasarkan bentuknya, meskipun saya tidak berpikir bahwa mungkin untuk mengimplementasikan proyek ini dengannya, karena tidak mungkin untuk menggunakan tepi yang ditentukan secara ketat dan tidak dapat dikaitkan dengan penerangan bangunan.