Sebuah artikel dari tim Stitch Fix menyarankan menggunakan pendekatan penelitian klinis uji coba non-inferioritas dalam pemasaran dan tes A / B produk. Pendekatan ini benar-benar berlaku ketika kami menguji solusi baru yang memiliki kelebihan yang tidak dapat diukur dengan tes.
Contoh paling sederhana adalah keropos tulang. Misalnya, kami mengotomatiskan proses penugasan pelajaran pertama, tetapi kami tidak ingin terlalu sering menjatuhkan konversi. Atau kami menguji perubahan yang difokuskan pada satu segmen pengguna, sambil memastikan bahwa konversi di segmen lain tidak banyak tenggelam (ketika menguji beberapa hipotesis, jangan lupa tentang koreksi).
Memilih batas yang tepat dari efisiensi yang tidak kalah menambah kesulitan tambahan pada tahap desain pengujian. Pertanyaan tentang bagaimana memilih Δ dalam artikel tidak diungkapkan dengan baik. Tampaknya pilihan ini tidak sepenuhnya transparan dalam uji klinis.
Tinjauan publikasi medis tentang non-inferioritas melaporkan bahwa hanya dalam setengah dari publikasi pilihan perbatasan dibenarkan dan seringkali pembenaran ini ambigu atau tidak terperinci.
Bagaimanapun, pendekatan ini tampaknya menarik, karena dengan mengurangi ukuran sampel yang dibutuhkan, dapat meningkatkan kecepatan pengujian, dan, karenanya, kecepatan pengambilan keputusan. -
Daria Mukhina, analis produk untuk aplikasi seluler Skyeng.Tim Stitch Fix senang menguji berbagai hal. Seluruh komunitas teknologi, pada prinsipnya, suka melakukan tes. Versi situs mana yang menarik lebih banyak pengguna - A atau B? Apakah versi A dari model rekomendasi menghasilkan lebih banyak uang daripada versi B? Hampir selalu, untuk menguji hipotesis, kami menggunakan pendekatan paling sederhana dari kursus statistik dasar:
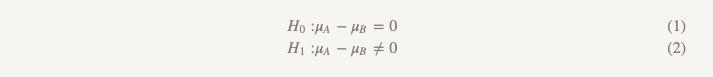
Meskipun kami jarang menggunakan istilah ini, bentuk pengujian ini disebut "hipotesis uji keunggulan". Dengan pendekatan ini, kami mengasumsikan bahwa tidak ada perbedaan antara dua opsi. Kami mematuhi ide ini dan menolaknya hanya jika data yang diperoleh cukup meyakinkan untuk ini - yaitu, mereka menunjukkan bahwa salah satu opsi (A atau B) lebih baik daripada yang lain.
Menguji hipotesis superioritas cocok untuk memecahkan banyak masalah. Kami merilis versi B dari model rekomendasi hanya jika itu jelas lebih baik daripada versi A. yang sudah digunakan. Tetapi dalam beberapa kasus pendekatan ini tidak bekerja dengan baik. Mari kita lihat beberapa contoh.
1) Kami menggunakan layanan pihak ketiga yang membantu mengidentifikasi kartu bank palsu. Kami menemukan layanan lain yang harganya jauh lebih murah. Jika layanan yang lebih murah berfungsi sebaik layanan yang kami gunakan sekarang, kami akan memilihnya. Itu tidak harus lebih baik dari layanan yang digunakan.
2) Kami ingin meninggalkan sumber data A dan menggantinya dengan sumber data B. Kami dapat menunda meninggalkan A jika B menghasilkan hasil yang sangat buruk, tetapi tidak mungkin untuk terus menggunakan A.
3) Kami ingin beralih dari pendekatan ke pemodelan A ke pendekatan B bukan karena kami mengharapkan hasil yang lebih baik dari B, tetapi karena itu memberi kami fleksibilitas operasional yang besar. Kami tidak punya alasan untuk percaya bahwa B akan lebih buruk, tetapi kami tidak akan memulai transisi jika ini masalahnya.
4) Kami membuat beberapa perubahan kualitatif pada desain situs web (versi B) dan kami percaya bahwa versi ini lebih unggul daripada versi A. Kami tidak mengharapkan perubahan dalam konversi atau indikator kinerja utama apa pun yang biasanya kami gunakan untuk mengevaluasi situs web. Tetapi kami percaya bahwa ada keuntungan dalam parameter yang beragam, atau teknologi kami tidak cukup untuk mengukur.
Dalam semua kasus ini, meneliti keunggulan bukanlah solusi terbaik. Tetapi kebanyakan ahli dalam situasi ini menggunakannya secara default. Kami dengan hati-hati melakukan percobaan untuk menentukan besarnya efek dengan benar. Jika benar bahwa versi A dan B bekerja sangat mirip, ada kemungkinan bahwa kita tidak akan dapat menolak hipotesis nol. Apakah kita menyimpulkan bahwa A dan B umumnya bekerja sama? Tidak! Ketidakmampuan untuk menolak hipotesis nol dan adopsi hipotesis nol bukanlah hal yang sama.
Perhitungan ukuran sampel (yang Anda, tentu saja dilakukan) biasanya dilakukan dengan batas yang lebih ketat untuk kesalahan jenis pertama (probabilitas penolakan salah hipotesis nol, sering disebut alpha) daripada kesalahan jenis kedua (probabilitas kegagalan untuk menolak hipotesis nol, ketika dengan asumsi bahwa hipotesis nol salah, sering disebut beta). Nilai khas untuk alpha adalah 0,05, sedangkan nilai khas untuk beta adalah 0,20, yang sesuai dengan kekuatan statistik 0,80. Ini berarti bahwa dengan kami, kami tidak dapat mendeteksi pengaruh sebenarnya dari nilai yang kami tunjukkan dalam perhitungan daya kami dengan probabilitas 20% dan ini adalah kesenjangan informasi yang cukup serius. Sebagai contoh, mari kita pertimbangkan hipotesis berikut:
H0: ransel saya TIDAK ada di kamar saya (3)
H1: ransel saya ada di kamar saya (4)Jika saya mencari di kamar saya dan menemukan ransel saya - baik, saya bisa menolak hipotesis nol. Tetapi jika saya melihat sekeliling ruangan dan tidak dapat menemukan ransel saya (Gambar 1), kesimpulan apa yang harus saya ambil? Apa aku yakin dia tidak ada di sana? Sudahkah saya cukup mencari? Bagaimana jika saya mencari hanya 80% ruangan? Untuk menyimpulkan bahwa ransel pasti tidak di dalam ruangan akan menjadi keputusan yang terburu-buru. Tidak mengherankan, kita tidak dapat "menerima hipotesis nol."
Area yang kami cari
Kami tidak menemukan ransel - haruskah kami menerima hipotesis nol?Gambar 1. Mencari 80% ruangan hampir sama dengan melakukan studi dengan kapasitas 80%. Jika Anda tidak menemukan tas punggung, setelah memeriksa 80% ruangan, apakah mungkin menyimpulkan bahwa tas itu tidak ada di sana?Jadi apa yang dilakukan spesialis data dalam situasi ini? Anda dapat sangat meningkatkan kekuatan penelitian, tetapi kemudian Anda akan membutuhkan sampel yang jauh lebih besar, dan hasilnya akan tetap tidak memuaskan.
Untungnya, masalah seperti itu telah lama dipelajari dalam dunia penelitian klinis. Obat B lebih murah daripada obat A; obat B diperkirakan menyebabkan efek samping yang lebih sedikit daripada obat A; obat B lebih mudah diangkut karena tidak perlu disimpan di lemari es, dan obat A diperlukan. Kami menguji hipotesis efisiensi tidak kurang. Hal ini diperlukan untuk menunjukkan bahwa versi B sama baiknya dengan versi A - setidaknya dalam batas tertentu “efisiensi yang tidak kalah”, Δ. Beberapa saat kemudian kita akan berbicara lebih banyak tentang cara menetapkan batas ini. Tetapi sekarang anggaplah ini adalah perbedaan terkecil yang secara praktis signifikan (dalam konteks uji klinis, ini biasanya disebut relevansi klinis).
Hipotesis efisiensi yang tidak kalah membuat segalanya terbalik:
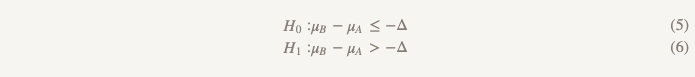
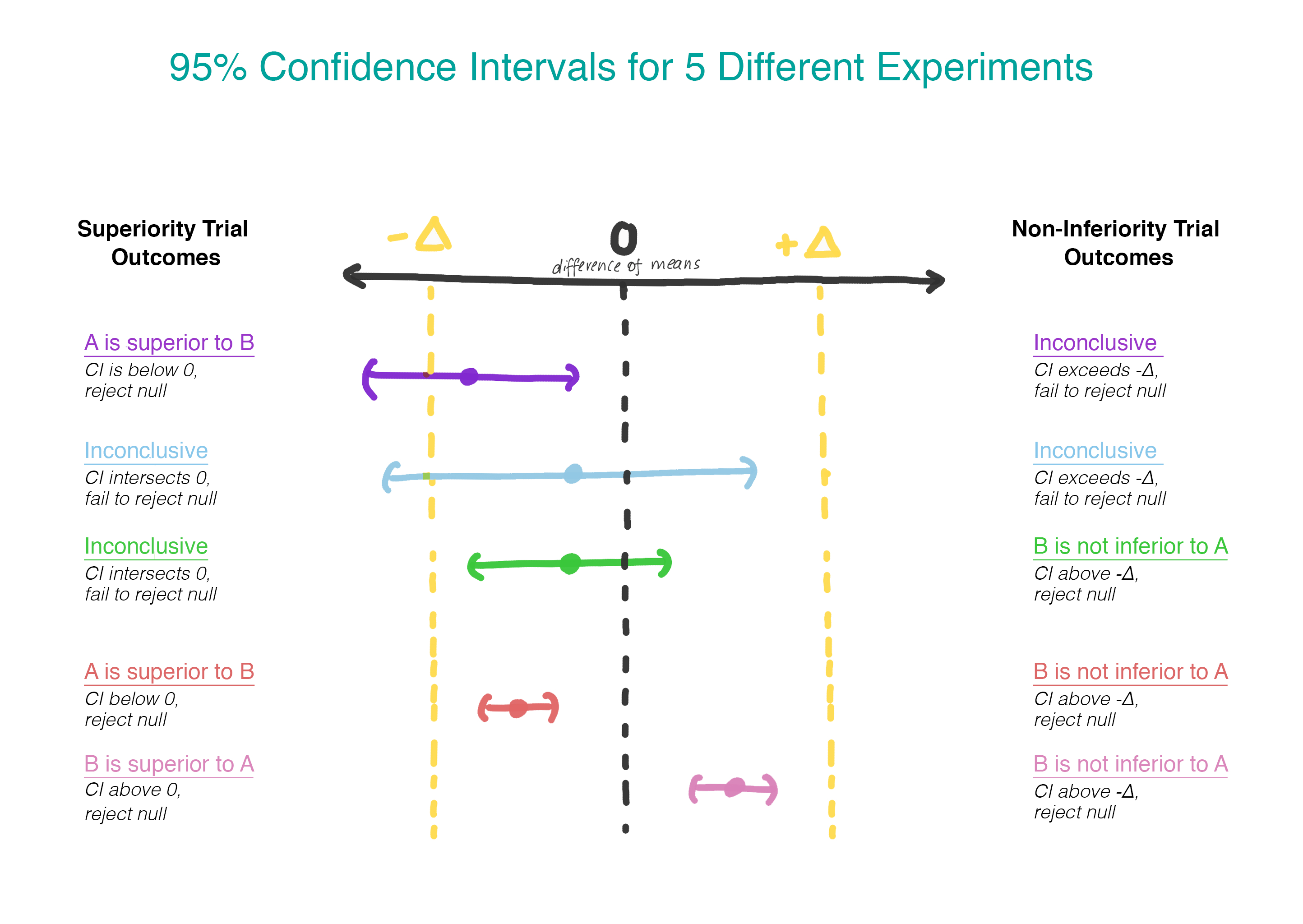
Sekarang, alih-alih mengasumsikan bahwa tidak ada perbedaan, kami menganggap bahwa versi B lebih buruk daripada versi A, dan kami akan tetap berpegang pada asumsi ini sampai kami menunjukkan bahwa itu tidak benar. Inilah saat ketika masuk akal untuk menggunakan pengujian hipotesis satu sisi! Dalam praktiknya, ini dapat dilakukan dengan membangun interval kepercayaan dan menentukan apakah intervalnya benar-benar lebih besar dari Δ (Gambar 2).
Δ pemilihan
Bagaimana cara memilih Δ? Proses seleksi Δ termasuk pembenaran statistik dan evaluasi subjek. Ada rekomendasi normatif dalam dunia uji klinis, yang darinya delta tersebut harus menjadi perbedaan terkecil yang signifikan secara klinis - yang akan relevan dalam praktiknya. Berikut ini adalah kutipan dari kepemimpinan Eropa, yang dapat Anda periksa sendiri: “Jika perbedaannya dipilih dengan benar, interval kepercayaan yang sepenuhnya terletak antara –∆ dan 0 ... masih cukup untuk menunjukkan efisiensi yang tidak kalah. Jika hasil ini tampaknya tidak dapat diterima, itu berarti ∆ tidak dipilih dengan tepat. "
Delta harus benar-benar tidak melebihi besarnya pengaruh versi A dalam kaitannya dengan kontrol yang benar (plasebo / kurangnya perawatan), karena ini membuat kita percaya bahwa versi B lebih buruk daripada kontrol yang benar dan pada saat yang sama menunjukkan “tidak kurang efisiensi”. Misalkan ketika versi A diperkenalkan, versi 0 ada di tempatnya atau fungsinya tidak ada sama sekali (lihat Gambar 3).
Berdasarkan hasil pengujian hipotesis superioritas, besarnya efek E terungkap (yaitu, mungkin μ ^ A - μ ^ 0 = E). Sekarang A adalah standar baru kami, dan kami ingin memastikan bahwa B tidak kalah dengan A. Cara lain untuk menulis μB - μA≤ - Δ (hipotesis nol) adalah μB≤μA - Δ. Jika kita menganggap bahwa melakukan sama dengan atau lebih besar dari E, maka μB ≤ μA - E ≤ plasebo. Sekarang kita melihat bahwa perkiraan kami untuk μB sepenuhnya melebihi μA - E, yang dengan demikian sepenuhnya menolak hipotesis nol dan memungkinkan kita untuk menyimpulkan bahwa B tidak kalah dengan A, tetapi pada saat yang sama, μB mungkin ≤ μ plasebo, tetapi ini bukan apa yang kita butuhkan (gambar 3).
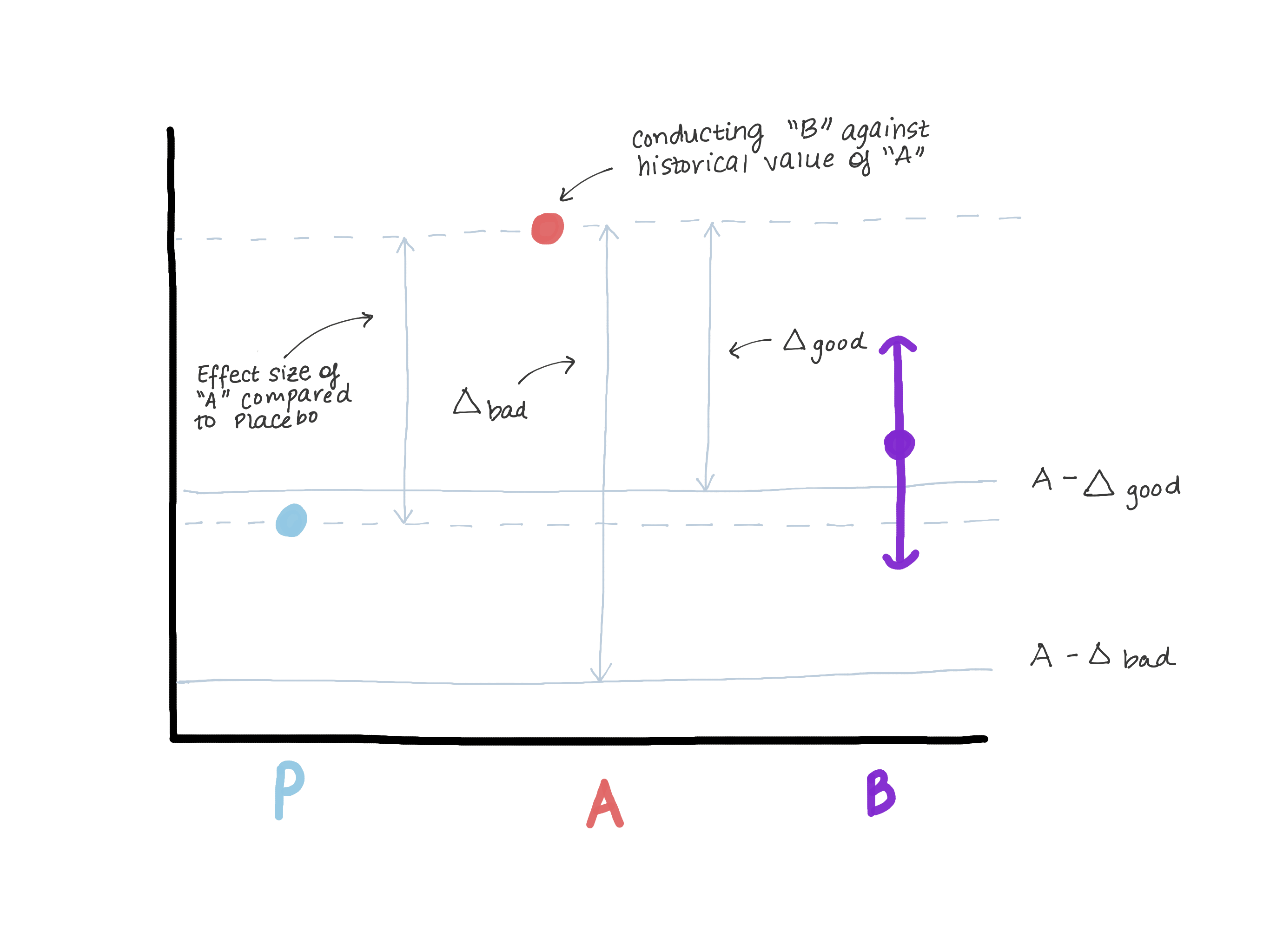Gambar 3. Demonstrasi risiko memilih batas efisiensi yang tidak kalah. Jika batasnya terlalu besar, kita dapat menyimpulkan bahwa B tidak kalah dengan A, tetapi pada saat yang sama tidak dapat dibedakan dari plasebo. Kami tidak akan mengubah obat, yang jelas lebih efektif daripada plasebo (A), pada obat, yang memiliki efektivitas yang sama dengan plasebo.Memilih α
Kami lolos ke pilihan α. Anda dapat menggunakan nilai standar α = 0,05, tetapi ini tidak sepenuhnya jujur. Seperti, misalnya, ketika Anda membeli sesuatu di Internet dan menggunakan beberapa kode diskon sekaligus, meskipun tidak harus diringkas, pengembang hanya membuat kesalahan dan Anda lolos begitu saja. Menurut aturan, nilai α harus sama dengan setengah nilai α, yang digunakan untuk menguji hipotesis superioritas, yaitu 0,05 / 2 = 0,025.
Ukuran sampel
Bagaimana cara memperkirakan ukuran sampel? Jika Anda percaya bahwa perbedaan rata-rata sebenarnya antara A dan B adalah 0, maka perhitungan ukuran sampel akan sama seperti ketika menguji hipotesis superioritas, kecuali bahwa Anda mengganti ukuran efek dengan batas efisiensi yang tidak kalah, asalkan Anda gunakan
α tidak kurang efisiensi = 1/2 superioritas (αnon-inferiority = 1/2 superior). Jika Anda memiliki alasan untuk percaya bahwa opsi B mungkin sedikit lebih buruk daripada opsi A, tetapi Anda ingin membuktikan bahwa itu lebih buruk dengan tidak lebih dari Δ, maka Anda beruntung! Faktanya, ini mengurangi ukuran sampel Anda, karena lebih mudah untuk menunjukkan bahwa B lebih buruk daripada A jika Anda benar-benar berpikir bahwa itu sedikit lebih buruk dan tidak setara.
Contoh Solusi
Misalkan Anda ingin beralih ke versi B, asalkan lebih buruk daripada versi A dengan tidak lebih dari 0,1 poin pada skala kepuasan pelanggan 5 poin ... Kami akan mendekati tugas ini menggunakan hipotesis superioritas.
Untuk menguji hipotesis superioritas, kami akan menghitung ukuran sampel sebagai berikut:
Artinya, jika Anda memiliki 2.103 pengamatan di grup Anda, Anda dapat 90% yakin bahwa Anda akan menemukan efek 0,10 atau lebih. Tetapi jika nilai 0,10 terlalu besar untuk Anda, mungkin Anda tidak boleh menguji hipotesis superioritas untuk itu. Mungkin, untuk keandalan, Anda memutuskan untuk melakukan studi untuk ukuran efek yang lebih kecil, misalnya, 0,05. Dalam hal ini, Anda akan memerlukan 8407 pengamatan, yaitu, sampel akan meningkat hampir 4 kali lipat. Tetapi bagaimana jika kita tetap pada ukuran sampel asli kita, tetapi meningkatkan kekuatan ke 0,99 sehingga kita tidak ragu apakah kita mendapatkan hasil yang positif? Dalam hal ini, n untuk satu kelompok akan menjadi 3676, yang lebih baik, tetapi meningkatkan ukuran sampel lebih dari 50%. Dan sebagai hasilnya, kita semua sama saja tidak dapat menyangkal hipotesis nol, dan tidak mendapatkan jawaban atas pertanyaan kita.
Bagaimana jika, sebaliknya, kami menguji hipotesis yang tidak kalah efektifnya?
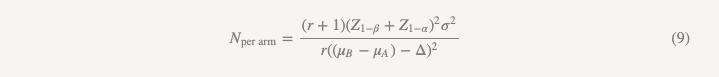
Ukuran sampel akan dihitung menggunakan rumus yang sama dengan pengecualian penyebut.
Perbedaan dari rumus yang digunakan untuk menguji hipotesis superioritas adalah sebagai berikut:
- Z1 - α / 2 digantikan oleh Z1 - α, tetapi jika Anda melakukan semuanya sesuai aturan, Anda mengganti α = 0,05 dengan α = 0,025, artinya, ini adalah angka yang sama (1,96)
- muncul di penyebut (μB - μA)
- θ (besarnya efek) diganti oleh Δ (batas efisiensi tidak kurang)
Jika kita mengasumsikan bahwa μB = µA, maka (µB - µA) = 0 dan menghitung ukuran sampel untuk batas efisiensi yang tidak kalah persis dengan apa yang akan kita dapatkan ketika menghitung keunggulan untuk nilai efek 0,1, hebat! Kita dapat melakukan penelitian dengan skala yang sama dengan hipotesis berbeda dan pendekatan kesimpulan yang berbeda, dan kita akan mendapatkan jawaban untuk pertanyaan yang benar-benar ingin kita jawab.
Sekarang anggaplah kita tidak benar-benar berpikir bahwa μB = µA dan
kami berpikir bahwa μB sedikit lebih buruk, mungkin 0,01 unit. Ini meningkatkan penyebut kami, mengurangi ukuran sampel per kelompok menjadi 1737.
Apa yang terjadi jika versi B sebenarnya lebih baik daripada versi A? Kami membantah hipotesis nol bahwa B lebih buruk daripada A lebih dari Δ dan menerima hipotesis alternatif bahwa B, jika lebih buruk, tidak lebih buruk daripada Δ, dan bisa lebih baik. Coba letakkan kesimpulan ini dalam presentasi lintas-fungsional dan lihat apa yang datang darinya (serius, cobalah). Dalam situasi di mana Anda perlu fokus pada masa depan, tidak ada yang mau setuju untuk "lebih buruk dengan tidak lebih dari Δ dan, mungkin, lebih baik."
Dalam hal ini, kita dapat melakukan penelitian, yang disebut sangat singkat "menguji hipotesis bahwa salah satu opsi lebih unggul daripada yang lain atau lebih rendah daripada itu." Ini menggunakan dua set hipotesis:
Set pertama (sama seperti saat menguji hipotesis efisiensi tidak kurang):
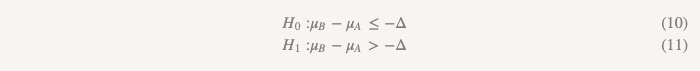
Set kedua (sama seperti saat menguji hipotesis superioritas):
Kami menguji hipotesis kedua hanya jika yang pertama ditolak. Dalam pengujian berurutan, kami mempertahankan tingkat kesalahan keseluruhan dari jenis pertama (α). Dalam praktiknya, ini dapat dicapai dengan membuat interval kepercayaan 95% untuk perbedaan antara rata-rata dan memeriksa untuk menentukan apakah seluruh interval melebihi -Δ. Jika intervalnya tidak melebihi -Δ, kita tidak bisa menolak nilai nol dan berhenti. Jika seluruh interval benar-benar melebihi −Δ, kami melanjutkan dan melihat apakah interval tersebut berisi 0.
Ada jenis penelitian lain yang belum kita diskusikan - studi kesetaraan.
Studi jenis ini dapat diganti dengan studi untuk menguji hipotesis yang tidak kalah efektifnya dan sebaliknya, tetapi pada kenyataannya mereka memiliki perbedaan penting. Pengujian untuk menguji hipotesis efisiensi yang tidak kalah bertujuan untuk menunjukkan bahwa opsi B setidaknya sama bagusnya dengan A. Dan studi kesetaraan bertujuan menunjukkan bahwa opsi B setidaknya sebaik A, dan opsi A sama baiknya dengan B, yang lebih rumit. Pada dasarnya, kami mencoba menentukan apakah seluruh interval kepercayaan terletak pada perbedaan rata-rata antara −Δ dan Δ. Studi semacam itu membutuhkan ukuran sampel yang lebih besar dan lebih jarang. Oleh karena itu, lain kali Anda melakukan studi di mana tugas utama Anda adalah memastikan bahwa versi yang baru tidak lebih buruk, jangan puas dengan "ketidakmampuan untuk menyangkal hipotesis nol." Jika Anda ingin menguji hipotesis yang sangat penting., Pertimbangkan berbagai opsi.