
Hai, habrozhiteli! Marcos Lopez de Prado membagikan apa yang biasanya mereka sembunyikan - algoritma pembelajaran mesin paling menguntungkan yang telah ia gunakan selama dua dekade untuk mengelola kumpulan dana besar dari para investor yang paling menuntut.
Pembelajaran mesin mengubah hampir setiap aspek kehidupan kita; Algoritma MO melakukan tugas yang, sampai saat ini, hanya dipercaya oleh para ahli tepercaya. Dalam waktu dekat, pembelajaran mesin akan mendominasi keuangan, peramalan nasib akan menjadi bagian dari masa lalu, dan investasi tidak lagi identik dengan perjudian.
Ambil kesempatan untuk berpartisipasi dalam "revolusi mesin", untuk ini cukup berkenalan dengan buku pertama, yang menyediakan analisis lengkap dan sistematis metode pembelajaran mesin dalam kaitannya dengan keuangan: mulai dengan struktur data keuangan, penandaan seri keuangan, penimbangan sampel, pembeda seri waktu ... dan diakhiri dengan seluruh bagian didedikasikan untuk pengujian strategi investasi yang benar.
Kutipan. Memahami Strategi Risiko
15.1. Relevansi
Strategi investasi sering diterapkan dalam hal posisi yang dipegang sampai salah satu dari dua kondisi terpenuhi: 1) kondisi untuk meninggalkan posisi dengan keuntungan (mengambil keuntungan) atau 2) kondisi untuk meninggalkan posisi dengan kerugian (menghentikan kerugian). Bahkan ketika strategi tidak secara eksplisit menyatakan stop loss, selalu ada batas stop loss implisit di mana investor tidak dapat lagi membiayai posisinya (margin call) atau menimbulkan kerusakan yang disebabkan oleh peningkatan kerugian yang belum direalisasi. Karena sebagian besar strategi memiliki (secara eksplisit atau implisit) kedua kondisi keluar ini, masuk akal untuk memodelkan distribusi hasil melalui proses binomial. Ini, pada gilirannya, akan membantu kami memahami kombinasi dari nilai taruhan, risiko, dan pembayaran yang tidak ekonomis. Tujuan bab ini adalah untuk membantu Anda mengevaluasi ketika strategi rentan terhadap perubahan kecil dalam jumlah ini.
Pertimbangkan strategi yang menghasilkan n taruhan yang terdistribusi secara identik dan saling independen per tahun, di mana hasil Xi dari taruhan i ∈ [1, n] adalah laba π> 0 dengan probabilitas P [Xi = π] = p dan kerugian –π dengan probabilitas P [Xi = –Π] = 1 - hal. Anda dapat membayangkan p sebagai keakuratan classifier biner, di mana hasil afirmatif berarti bertaruh atas peluang, dan hasil negatif berarti kehilangan peluang: pernyataan benar dihargai, pernyataan palsu dihukum, dan hasil negatif (apakah benar atau salah) tidak memiliki imbalan. Karena hasil dari taruhan {Xi} i = 1, ..., n adalah independen, kami akan menghitung momen yang diharapkan per taruhan. Keuntungan yang diharapkan dari satu taruhan adalah E [Xi] = πp + (–π) (1 - p) = π (2p - 1). Perbedaannya adalah
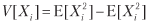
dimana
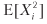
= π2p + (–π) 2 (1 - p) = π2, oleh karena itu, V [Xi] = π2 - π2 (2p - 1) 2 = π2 [1– (2p - 1) 2] = 4π2p (1 - p ) Untuk n yang terdistribusi secara identik, tingkat yang saling independen per tahun, rasio Sharpe tahunan rata-rata (θ) adalah
Perhatikan bagaimana π menyeimbangkan persamaan di atas karena pembayarannya simetris. Seperti dalam kasus Gaussian, θ [p, n] dapat dipahami sebagai nilai-t skala ulang1. Ini menggambarkan fakta bahwa bahkan untuk kecil
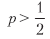
rasio Sharpe dapat dibuat tinggi untuk n yang cukup besar. Ini berfungsi sebagai basis ekonomi untuk perdagangan frekuensi tinggi, di mana p bisa sedikit lebih tinggi dari 0,5, dan kunci untuk aktivitas pertukaran yang sukses adalah peningkatan n. Rasio Sharpe adalah fungsi akurasi, dan bukan kebenaran, karena melewatkan kesempatan (pernyataan negatif) tidak dihargai atau dihukum secara langsung (meskipun terlalu banyak pernyataan negatif dapat mengarah ke n kecil, yang akan mengurangi koefisien Sharpe menjadi nol).
Misalnya, untuk
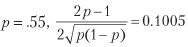
dan untuk mencapai rasio Sharpe tahunan rata-rata 2, 396 taruhan per tahun diperlukan. Listing 15.1 memverifikasi hasil ini secara eksperimental. Gambar 15.1 menunjukkan rasio Sharpe sebagai fungsi akurasi untuk frekuensi taruhan yang berbeda.
Listing 15.1. Rasio Sharpe sebagai fungsi dari jumlah taruhan
out,p=[],.55 for i in xrange(1000000): rnd=np.random.binomial(n=1,p=p) x=(1 if rnd==1 else -1) out.append(x) print np.mean(out),np.std(out),np.mean(out)/np.std(out)
Persamaan ini menyatakan dengan jelas trade-off antara akurasi (p) dan frekuensi (n) untuk koefisien Sharpe yang diberikan (θ). Misalnya, untuk memberikan rasio Sharpe tahunan rata-rata 2 untuk strategi yang hanya menghasilkan tarif mingguan (n = 52), diperlukan akurasi yang cukup tinggi p = 0,6336.
15.3. Pembayaran Asimetris
Pertimbangkan strategi yang menghasilkan n taruhan yang saling independen berdistribusi identik per tahun, di mana hasil Xi dari taruhan i ∈ [1, n] adalah π + dengan probabilitas P [Xi = π +] = p, dan hasilnya π– (π– <π + ) terjadi dengan probabilitas P [Xi = π_] = 1 - p. Keuntungan yang diharapkan dari satu taruhan adalah E [Xi] = pπ + + (1 - p) π– = (π + - π–) p + π–. Dispersi adalah V [Xi] =, di mana
Akhirnya, kita bisa menyelesaikan persamaan sebelumnya untuk 0 ≤ p ≤ 1 dan dapatkan
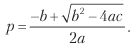
dimana:
a = (n + θ2) (π + - π–) 2;
b = [2nπ - θ2 (π + - π -)] (π + - π–);

Catatan: Listing 15.2 memverifikasi operasi simbolik ini menggunakan shell Live Python SymPy yang berjalan di layanan cloud Google App Engine:
live.sympy.org .
Listing 15.2. Menggunakan Perpustakaan SymPy untuk Operasi Simbolik
>>> from sympy import * >>> init_printing(use_unicode=False,wrap_line=False,no_global=True) >>> p,u,d=symbols('pu d') >>> m2=p*u**2+(1-p)*d**2 >>> m1=p*u+(1-p)*d >>> v=m2-m1**2 >>> factor(v)
Persamaan di atas menjawab pertanyaan berikut: untuk aturan perdagangan tertentu yang ditandai oleh parameter {π–, π +, n}, berapakah tingkat akurasi p yang diperlukan untuk mencapai rasio Sharpe sama dengan θ *? Misalnya, untuk mendapatkan θ = 2 untuk n = 260, π– = –.01, π + = .005, kita perlu p = .72. Karena banyaknya taruhan, perubahan yang sangat kecil pada p (dari p = .7 ke p = .72) mempromosikan rasio Sharpe dari θ = 1.173 ke θ = 2. Di sisi lain, ini juga memberi tahu kita bahwa strategi ini rentan terhadap kecil perubahan pada hal. Listing 15.3 mengimplementasikan derivasi dari akurasi yang diharapkan. Dalam gbr. 15.2 menunjukkan akurasi yang seharusnya sebagai fungsi dari n dan π–, di mana π + = 0,1, dan θ * = 1,5. Karena ambang π– menjadi lebih negatif untuk n yang diberikan, derajat p yang lebih tinggi diperlukan untuk mencapai θ * untuk ambang yang diberikan π +. Karena angka n menjadi lebih kecil untuk ambang tertentu π–, tingkat p yang lebih tinggi diperlukan untuk mencapai θ * untuk π + yang diberikan.
Listing 15.3. Perhitungan Taksiran Akurasi
def binHR(sl,pt,freq,tSR): ´´´
Untuk aturan perdagangan tertentu yang dicirikan oleh parameter {sl, pt, freq}, berapakah akurasi minimum yang diperlukan untuk mencapai rasio Sharpe sama dengan tSR?
1) Input
sl: ambang batas stop loss
pt: ambang batas laba
freq: jumlah taruhan per tahun
tSR: target rasio Sharpe rata-rata tahunan
2) Keluar
p: presisi minimum p diperlukan untuk mencapai tSR
´´´
a = (freq + tSR ** 2) * (pt-sl) ** 2
b = (2 * freq * sl-tSR ** 2 * (pt-sl)) * (pt-sl)
c = freq * sl ** 2
p = (- b + (b ** 2-4 * a * c) **. 5) / (2. * a)
return p
Listing 15.4 memecahkan θ [p, n, π–, π +] untuk perkiraan frekuensi taruhan n. Dalam gbr. 15.3 menunjukkan perkiraan frekuensi tergantung pada p dan π–, di mana π + = 0,1, dan θ * = 1,5. Ketika ambang π– menjadi lebih negatif untuk tingkat p yang diberikan, angka yang lebih tinggi n diperlukan untuk mencapai θ * untuk ambang yang diberikan π +. Ketika derajat p menjadi lebih kecil untuk ambang tertentu π–, angka yang lebih tinggi n diperlukan untuk mencapai θ * untuk ambang tertentu π +.
Listing 15.4. Menghitung Frekuensi Taruhan Estimasi
def binFreq(sl,pt,p,tSR): ´´´
Dengan aturan perdagangan yang ditandai dengan parameter {sl, pt, freq}, berapa banyak taruhan per tahun yang diperlukan untuk mencapai koefisien Sharp tSR dengan tingkat akurasi p?
Catatan: persamaan dengan radikal, periksa solusi asing.
1) Input
sl: ambang batas stop loss
pt: ambang batas laba
p: tingkat akurasi p
tSR: target rasio Sharpe rata-rata tahunan
2) Keluar
freq: jumlah taruhan yang dibutuhkan per tahun
´´´
freq = (tSR * (pt-sl)) ** 2 * p * (1-p) / ((pt-sl) * p + sl) ** 2 # mungkin asing
jika tidak np.isclose (binSR (sl, pt, freq, p), tSR): return
mengembalikan freq
»Informasi lebih lanjut tentang buku ini dapat ditemukan di
situs web penerbit»
Isi»
KutipanKupon diskon 25% untuk penjaja -
Pembelajaran MesinSetelah pembayaran versi kertas buku, versi elektronik buku dikirim melalui email.