
Sejak dirilis pada Agustus 2018, Julia telah secara aktif mendapatkan popularitas dengan memasukkan 10 bahasa teratas di Github dan 20 keterampilan profesional paling populer menurut Upwork . Untuk pemula, kursus mulai dan buku diterbitkan . Julia digunakan untuk perencanaan misi ruang angkasa , farmakometri, dan pemodelan iklim .
Sebelum melanjutkan ke komputasi terdistribusi di Julia, mari kita beralih ke pengalaman mereka yang telah mencoba kesempatan PL baru ini untuk masalah yang diterapkan - dari persamaan difusi pada dua inti, ke peta astronomi pada superkomputer.
Komputasi Paralel dan Faktor-Faktor yang Mempengaruhi Kinerja Komputasi Paralel
Sebagian besar komputer modern memiliki lebih dari satu prosesor, dan beberapa komputer dapat digabungkan menjadi sebuah cluster. Menggunakan kekuatan beberapa prosesor memungkinkan Anda untuk melakukan banyak perhitungan lebih cepat. Kinerja dipengaruhi oleh dua faktor utama: kecepatan prosesor itu sendiri dan kecepatan akses memori mereka. Dalam sebuah cluster, CPU ini akan memiliki akses tercepat ke RAM yang terletak di komputer atau host yang sama. Yang lebih mengejutkan, masalah seperti itu relevan pada laptop multi-core khas karena perbedaan kecepatan memori utama dan cache. Oleh karena itu, lingkungan multiprosesor yang baik harus memungkinkan Anda untuk mengontrol penggunaan bagian memori oleh prosesor tertentu.
Komputasi Paralel di Julia
Julia memiliki beberapa primitif bawaan untuk komputasi paralel di setiap tingkat: vektorisasi (SIMD), multithreading, dan komputasi terdistribusi.
Multithreading milik Julia sendiri memungkinkan pengguna untuk menggunakan kemampuan laptop multi-core, sedangkan panggilan jarak jauh dan primitif akses jarak jauh memungkinkan Anda untuk mendistribusikan pekerjaan di antara banyak proses dalam cluster. Selain primitif bawaan ini, sejumlah paket di ekosistem Julia menyediakan pemrosesan paralel yang efisien.
Vektorisasi otomatis di Julia
Chip Intel modern menyediakan sejumlah ekstensi set perintah. Diantaranya adalah berbagai versi Streaming SIMD Extension (SSE) dan beberapa generasi ekstensi vektor (tersedia dalam keluarga prosesor terbaru). Ekstensi ini menyediakan pemrograman dengan gaya Single Instruction Multiple Data (SIMD) , memberikan akselerasi yang signifikan untuk kode yang cocok dengan gaya pemrograman seperti itu. Kompiler Julia LLia yang tangguh dapat secara otomatis menghasilkan kode mesin yang sangat efisien untuk fungsi-fungsi dasar dan yang ditentukan pengguna pada arsitektur apa pun, seperti SIMD Hardware (didukung oleh LLVM ), yang memungkinkan pengguna untuk lebih sedikit khawatir tentang penulisan kode khusus untuk masing-masing arsitektur ini. Keuntungan lain dari menggunakan kompiler untuk meningkatkan kinerja, daripada secara manual mengkodekan "hot loop" dalam suatu perakitan, adalah bahwa itu jauh lebih baik untuk masa depan. Setiap kali arsitektur kumpulan instruksi generasi berikutnya keluar, kode khusus Julia secara otomatis menjadi lebih cepat.
Multithreading
Multithreading di Julia biasanya berbentuk loop paralel. Ada juga primitif untuk kunci dan atom yang memungkinkan pengguna untuk menyinkronkan kode mereka. Primitif paralel Julia sederhana namun kuat. Terlihat bahwa mereka menskalakan hingga ribuan node dan memproses terabyte data .
Komputasi terdistribusi
Meskipun primitif bawaan Julia cukup untuk penyebaran paralel berskala besar, ada sejumlah paket untuk pekerjaan yang lebih khusus. ClusterManagers.jl menyediakan antarmuka untuk sejumlah sistem antrian pekerjaan yang biasa digunakan dalam komputasi cluster, seperti Sun Grid Engine dan Slurm . DistributedArrays.jl menyediakan antarmuka yang nyaman untuk array data yang didistribusikan di seluruh cluster. Ini menggabungkan sumber daya memori dari beberapa mesin, yang memungkinkan untuk menggunakan array yang terlalu besar untuk muat pada satu mesin. Setiap proses berjalan pada bagian array yang dimilikinya, memberikan jawaban yang siap pakai untuk pertanyaan tentang bagaimana program harus dibagi antara mesin.
Dalam beberapa aplikasi lama, pengguna memilih untuk tidak memikirkan kembali model paralel mereka dan ingin terus menggunakan konkurensi gaya MPI . Bagi mereka, MPI.jl menyediakan pembungkus tipis di sekitar MPI yang memungkinkan pengguna untuk menggunakan prosedur penyampaian pesan gaya MPI.
Julia dalam pertempuran
Proyek Celeste adalah kolaborasi antara Julia Computing, Intel Labs, JuliaLabs @ MIT, Lawrence Berkeley National Labs dan University of California di Berkeley.
Celeste adalah model hierarkis yang sepenuhnya generatif yang menggunakan inferensi statistik untuk menentukan secara matematis lokasi dan karakteristik sumber cahaya di langit. Model ini memungkinkan para astronom mengidentifikasi galaksi yang menjanjikan untuk menargetkan spektograf dan membantu memahami peran energi gelap, materi gelap, dan geometri alam semesta.

Contoh dari Sloan Digital Sky Survey (SDSS)
Menggunakan kemampuan komputasi paralel Julia sendiri, tim peneliti Celeste memproses 55 terabyte data visual dan mengklasifikasikan 188 juta objek astronomi hanya dalam 15 menit, menghasilkan katalog lengkap pertama dari semua objek yang terlihat dari Sloan Digital Sky Survey . Ini adalah salah satu masalah optimisasi matematika terbesar yang pernah dipecahkan oleh umat manusia.

Proyek Celeste menggunakan 9.300 Knights Landing (KNL) node pada superkomputer NERSC Cori Phase II untuk mengeksekusi 1,3 juta thread pada 650.000 KNL core, yang menggabungkan daftar aplikasi dengan kecepatan melebihi 1 petaflops per detik , menjadikan Julia satu-satunya yang dinamis bahasa tingkat tinggi yang pernah mencapai prestasi seperti itu. ?? Tetapi apakah sinkronisasi teleskop dan pemrosesan data untuk gambar lubang hitam pada 10.04.19 memecahkan rekor ini? Sepertinya Python banyak digunakan di sana.
Pemrograman paralel dengan Julia menggunakan MPI
Terjemahan bahan dari blog fisika plasma Claudio 2018-09-30
Julia telah ada sejak 2012, dan setelah lebih dari enam tahun pengembangan, versi 1.0 akhirnya dirilis. Ini adalah tahap penting yang menginspirasi saya untuk membuat posting baru (setelah beberapa bulan hening). Kali ini kita akan melihat bagaimana melakukan pemrograman paralel di Julia menggunakan paradigma message passing interface (MPI) melalui perpustakaan open source MPI Terbuka. Kami akan melakukan ini dengan memecahkan masalah fisik nyata: difusi panas melalui wilayah dua dimensi.

Gambar 1. Superkomputer Sequoia di LLNL dengan hampir 1,6 juta prosesor tersedia untuk simulasi numerik senjata nuklir. hpc.llnl.gov
Ini akan menjadi aplikasi MPI yang cukup canggih, yang ditujukan bagi mereka yang sudah memiliki pemahaman tentang komputasi paralel. Karena itu, saya tidak akan pergi selangkah demi selangkah, tetapi lebih fokus pada aspek-aspek spesifik yang, menurut pendapat saya, menarik (khususnya, penggunaan sel hantu dan transmisi pesan dalam kisi dua dimensi). Mengikuti tradisi postingan terbarunya, kode yang dibahas di sini hanya akan ditata sebagian. Ini disertai dengan solusi berfitur lengkap yang dapat Anda temukan di Github - Diffusion.jl .
Komputasi paralel telah memasuki "dunia komersial" selama beberapa tahun terakhir. Ini adalah solusi standar untuk aplikasi ETL (Extract-Transform-Load), di mana masalah yang dipertimbangkan paralel paralelnya memalukan: setiap proses dilakukan secara independen dari yang lain, dan tidak ada koneksi jaringan yang diperlukan (sampai langkah "reduksi" akhir terjadi, di mana setiap solusi lokal berkumpul di solusi global).
Dalam banyak aplikasi ilmiah, perlu untuk mengirimkan informasi melalui jaringan cluster. Masalah "pemerasan paralel" ini sering merupakan simulasi numerik: masalah astrofisika, pemodelan cuaca, biologi, sistem kuantum, dll. Dalam beberapa kasus, simulasi ini dilakukan pada puluhan dan bahkan jutaan prosesor (Gbr. 1), dan memori didistribusikan di antara prosesor yang berbeda. Biasanya, prosesor ini berinteraksi dalam superkomputer melalui paradigma message passing interface (MPI).
Siapa pun yang bekerja dalam komputasi kinerja tinggi harus terbiasa dengan MPI. Ini memungkinkan penggunaan arsitektur cluster pada tingkat yang sangat rendah. Secara teoritis, seorang peneliti dapat menetapkan masing-masing CPU beban komputasi sendiri. Ia dapat memutuskan kapan dan informasi apa yang harus ditransfer antara prosesor, dan apakah ini harus terjadi secara sinkron atau tidak sinkron.
Dan sekarang mari kita kembali ke isi posting ini, di mana kita akan melihat bagaimana menulis solusi untuk persamaan tipe difusi menggunakan MPI. Kami telah membahas skema eksplisit untuk persamaan satu dimensi dari tipe ini ( Omong-omong, kami juga membahas ini ). Namun, dalam posting ini kami akan mempertimbangkan solusi dua dimensi.
Kode Julia yang disajikan di sini pada dasarnya adalah terjemahan dari kode C / Fortran yang dijelaskan dalam pos luar biasa oleh Fabien Durnak.
Dalam posting ini saya tidak akan menganalisis secara rinci kecepatan penskalaan dan jumlah prosesor. Terutama karena saya hanya memiliki dua prosesor yang dapat saya mainkan di rumah (prosesor Intel Core i7 pada MacBook Pro saya) ... Namun, saya masih dapat dengan bangga mengatakan bahwa kode Julia disajikan dalam posting ini, menunjukkan akselerasi yang signifikan ketika menggunakan dua prosesor melawan satu. Pokoknya: lebih cepat dari kode Fortran dan C yang setara! (lebih lanjut tentang ini nanti)
Berikut adalah topik yang akan kita bahas dalam posting ini:
- Julia: Kesan pertamaku
- Cara menginstal Open MPI di komputer Anda
- Masalah: propagasi melalui domain dua dimensi
- Komunikasi antar-prosesor: kebutuhan sel hantu
- Menggunakan MPI
- Visualisasi solusi
- Performa
- Kesimpulan
1. Kesan pertama Julia
Bahkan, saya bertemu Julia baru-baru ini, jadi saya memutuskan untuk fokus pada beberapa "kesan pertama" di sini.
Alasan utama saya menjadi tertarik pada Julia adalah bahwa ia berjanji untuk menjadi kerangka kerja tujuan umum dengan kinerja yang sebanding dengan C dan Fortran , sambil menjaga fleksibilitas dan kemudahan penggunaan bahasa scripting seperti Matlab atau Python . Bahkan, Julia harus dapat menulis Data Science / aplikasi High-Performance-Computing yang berjalan di komputer lokal, di cloud, atau di superkomputer perusahaan.
Salah satu aspek yang saya tidak suka adalah alur kerja, yang tampaknya kurang optimal bagi mereka yang, seperti saya, menggunakan IntelliJ dan PyCharm setiap hari (plugin IntelliJ Julia sangat buruk). Saya juga mencoba Juno IDE , yang mungkin merupakan solusi terbaik saat ini, tetapi saya masih harus terbiasa dengannya.
Salah satu aspek yang menunjukkan bagaimana Julia belum mencapai "kedewasaannya" adalah seberapa bervariasi dan ketinggalan jaman dokumentasi banyak paket ( untuk paket yang telah disimpan, semuanya telah disekop sejak tahun lalu ). Saya masih belum menemukan cara untuk menulis matriks angka floating-point ke disk dalam bentuk yang diformat ( sekarang mudah ditemukan ). Tentu saja, Anda dapat menulis ke disk setiap elemen matriks dalam loop ganda, tetapi solusi yang lebih baik harus tersedia. Hanya saja informasi ini sulit ditemukan, dan dokumentasinya harus lengkap.
Aspek lain yang menonjol saat pertama kali Julia digunakan adalah pilihan menggunakan pengindeksan dari satu untuk array. Meskipun saya menemukan ini agak menjengkelkan dari sudut pandang praktis, itu tentu saja tidak melanggar perjanjian, mengingat itu tidak unik untuk Julia (Matlab dan Fortran juga menggunakan pengindeksan dimulai dengan satu).
Sekarang, untuk aspek yang baik dan paling penting: Julia bisa sangat cepat. Saya terkesan melihat bagaimana kode Julia yang saya tulis untuk posting ini dapat bekerja lebih baik daripada kode Fortran dan C yang setara, meskipun pada dasarnya saya hanya menerjemahkannya ke Julia. Lihatlah bagian kinerja jika Anda tertarik.
2. Instalasi Open MPI
Open MPI adalah pustaka antarmuka perpesanan sumber terbuka. Perpustakaan terkenal lainnya termasuk MPICH dan MVAPICH. Dikembangkan oleh Ohio State University, MVAPICH saat ini adalah perpustakaan yang paling canggih karena juga dapat mendukung cluster GPU - yang sangat berguna untuk aplikasi Deep Learning (memang, ada kolaborasi erat antara NVIDIA dan tim MVAPICH).
Semua pustaka ini dibangun di atas antarmuka yang umum: MPI API. Oleh karena itu, tidak masalah jika Anda menggunakan satu atau perpustakaan lain: kode yang Anda tulis mungkin tetap sama.
Proyek MPI.jl di Github adalah pembungkus untuk MPI. Di bawah tenda, ia menggunakan instalasi MPI C dan Fortran. Ini berfungsi dengan baik, meskipun tidak memiliki beberapa fitur yang tersedia dalam bahasa lain ini.
Untuk menjalankan MPI di Julia, Anda harus menginstal Open MPI secara terpisah di komputer Anda. Jika Anda memiliki Mac, saya menemukan panduan ini sangat berguna. Penting untuk dicatat bahwa Anda juga perlu menginstal gcc (kompiler GNU), karena Open MPI memerlukan kompiler Fortran dan C. Saya menginstal versi Open MPI 3.1.1, yang juga dikonfirmasi oleh mpiexec --version di terminal saya.
Setelah Open MPI diinstal pada komputer Anda, Anda harus menginstal cmake . Sekali lagi, jika Anda memiliki Mac, mengetik semudah brew install cmake di terminal Anda.
Saat ini, Anda siap untuk menginstal paket MPI di Julia. Buka Julia REPL dan ketik using Pkg Pkg.add («MPI») . Biasanya pada titik ini Anda harus dapat mengimpor paket menggunakan MPI untuk mengimpor. Namun, saya juga harus membangun paket melalui Pkg.build («MPI») sebelum berfungsi.
3. Masalah: persamaan difusi dua dimensi
Persamaan difusi adalah contoh persamaan diferensial parsial parabola. Dia menggambarkan fenomena seperti difusi panas atau difusi konsentrasi (hukum kedua Fick). Dalam dua dimensi spasial, persamaan difusi ditulis
Solusi menunjukkan bagaimana suhu / konsentrasi berubah (tergantung pada apakah kita mempelajari distribusi panas atau difusi zat) dalam ruang dan waktu. Memang, variabel x dan y mewakili koordinat spasial, dan komponen waktu diwakili oleh variabel t . Kuantitas D adalah "koefisien difusi" dan menentukan seberapa cepat, misalnya, panas akan merambat melalui wilayah fisik. Mirip dengan apa yang dibahas (lebih terinci) dalam posting blog sebelumnya, persamaan di atas dapat didiskritisasi menggunakan apa yang disebut "skema eksplisit" dari solusi. Saya tidak akan membahas rincian yang dapat Anda temukan di blog, cukup tulis solusi numerik dalam bentuk berikut:
di mana i dan k indeks yang berjalan di sepanjang grid spasial, j dalam waktu. Lapisan pertama kali diisi dari kondisi awal, dan masing-masing berikutnya dihitung menggunakan nilai-nilai dari lapisan sebelumnya. Dalam gambar, simpul merah menunjukkan simpul lapisan yang diperlukan untuk menghitung nilai pada titik tersebut

Persamaan (1) adalah benar-benar semua yang diperlukan untuk menemukan solusi atas seluruh area pada setiap langkah waktu berikutnya. Sangat sederhana untuk mengimplementasikan kode yang melakukan ini secara berurutan dengan satu proses pada CPU. Namun, di sini kami ingin membahas implementasi paralel yang menggunakan beberapa proses.
Setiap proses akan bertanggung jawab untuk menemukan solusi di bagian dari seluruh domain spasial. Masalah seperti difusi panas, yang tidak jelas kandidat untuk komputasi terdistribusi, memerlukan pertukaran informasi antar proses. Untuk memperjelas hal ini, mari kita lihat gambarnya
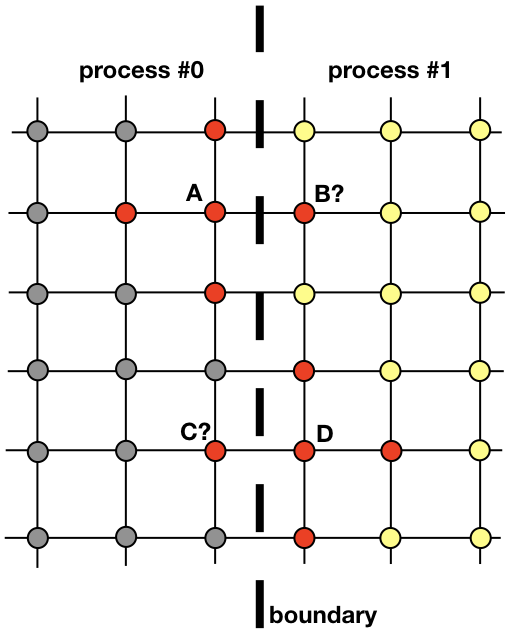
Dua proses tetangga harus berinteraksi untuk menemukan solusi di dekat perbatasan. Proses 0 harus mengetahui nilai solusi dalam B untuk menghitung solusi pada titik grid A. Demikian pula, proses 1 harus mengetahui nilai pada titik C untuk menghitung solusi pada titik grid D. Nilai-nilai ini tidak diketahui oleh proses sampai ada hubungan antara proses 0 dan 1 .
Ini menunjukkan bagaimana proses 0 dan 1 perlu berinteraksi untuk mengevaluasi solusi di dekat batas. Di sinilah MPI memasuki lokasi. Di bagian selanjutnya, kita akan melihat cara pengiriman pesan yang efektif.
4. Komunikasi antar proses: sel hantu
Konsep penting dalam dinamika fluida komputasi adalah konsep sel hantu. Konsep ini berguna setiap kali domain spasial didekomposisi menjadi beberapa subdomain, yang masing-masing diselesaikan dengan satu proses tunggal.
Untuk memahami apa itu sel hantu, mari kita lihat dua area tetangga di gambar sebelumnya lagi. Proses 0 bertanggung jawab untuk menemukan solusi di sisi kiri, sedangkan proses 1 menemukannya di sisi kanan domain spasial. Namun, karena bentuk stensil (Gbr. 2) di dekat perbatasan, kedua proses harus saling bertukar data. Inilah masalahnya: sangat tidak efisien bahwa proses 0 dan proses 1 berkomunikasi setiap kali mereka memerlukan simpul dari proses tetangga: ini akan menyebabkan biaya komunikasi yang tidak dapat diterima.
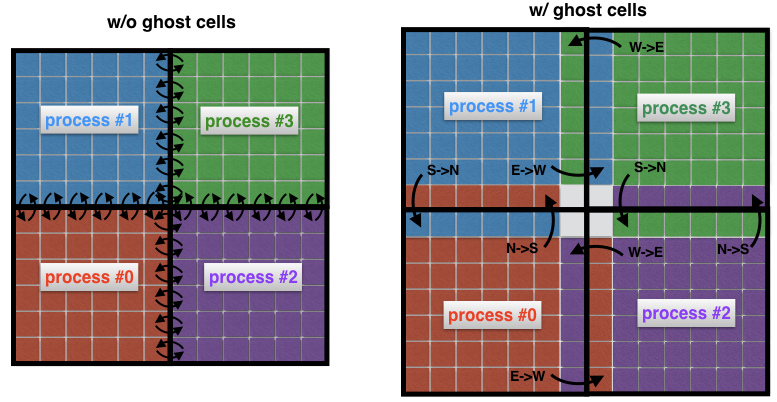
Gbr. 4 Koneksi antara proses tanpa (kiri) dan dengan sel hantu (kanan). Tanpa sel perantara, setiap sel di perbatasan subdomain harus mengirimkan pesannya sendiri ke proses tetangga. Menggunakan sel hantu memungkinkan Anda untuk meminimalkan jumlah pesan yang dikirimkan, karena banyak sel milik batas proses bertukar satu pesan sekaligus. Di sini, misalnya, proses 0 mentransfer seluruh batas utara ke proses 1, dan seluruh batas timur untuk memproses 2.
Sebagai gantinya, itu adalah praktik umum untuk mengelilingi subdomain "nyata" dengan sel tambahan yang disebut sel hantu, seperti yang ditunjukkan pada Gambar 4 (kanan). Sel-sel hantu ini adalah salinan dari solusi di perbatasan subdomain tetangga. Pada setiap langkah waktu, batas lama setiap subdomain diteruskan ke tetangga. Ini memungkinkan Anda untuk menghitung solusi baru di perbatasan subdomain dengan overhead komunikasi yang berkurang secara signifikan. Efek bersihnya adalah akselerasi kode.
5. Menggunakan MPI
Ada banyak tutorial MPI. Di sini saya hanya ingin menggambarkan perintah yang diekspresikan dalam bahasa shell MPI.jl untuk Julia yang saya gunakan untuk memecahkan masalah difusi dua dimensi. Ini adalah beberapa perintah dasar yang digunakan di hampir setiap implementasi MPI.
Perintah MPIMPI.init () - menginisialisasi runtime
MPI.COMM_WORLD - mewakili komunikator, mis., Semua proses yang tersedia melalui aplikasi MPI (setiap pesan harus dikaitkan dengan komunikator)
MPI.Comm_rank (MPI. COMM_WORLD) - menentukan peringkat internal (id) dari proses
MPI.Barrier (MPI.COMM_WORLD) - memblokir eksekusi hingga semua proses mencapai prosedur ini
MPI.Bcast! (Buf, n_buf, rank_root, MPI.COMM_WORLD) MPI.Bcast! (Buf, n_buf, rank_root, MPI.COMM_WORLD) - menyiarkan buf pesan penyangga dengan ukuran n_buf dari proses dengan peringkat rank_root ke semua proses lain di komunikator MPI.COMM_WORLD
MPI.Waitall! (reqs) MPI.Waitall! (reqs) - mengharapkan penyelesaian semua permintaan MPI (permintaan tersebut adalah descriptor, dengan kata lain, tautan, untuk transfer pesan asinkron)
MPI.REQUEST_NULL - menunjukkan bahwa permintaan tidak dikaitkan dengan koneksi yang sedang berlangsung
MPI.Gather (buf, rank_root, MPI.COMM_WORLD) - mengurangi variabel buf ke proses mendapatkan rank_root
MPI.Isend (buf, rank_dest, tag, MPI.COMM_WORL D) - pesan buf dikirim secara tidak sinkron dari proses saat ini ke proses rank_dest, dan pesan ditandai dengan parameter
MPI.Irecv! (Buf, rank_src, tag, MPI.COMM_WORLD) MPI.Irecv! (Buf, rank_src, tag, MPI.COMM_WORLD) - menerima pesan dengan tag tag dari proses sumber peringkat rank_src ke buffer buffer lokal
MPI.Finalize () - mengakhiri runtime MPI
5.1 Menemukan proses tetangga
Untuk tugas kami, kami akan menguraikan wilayah dua dimensi kami menjadi banyak subdomain persegi panjang, seperti yang ditunjukkan pada gambar di bawah ini.

Gambar 5. Dekomposisi kartesius dari wilayah dua dimensi dibagi menjadi 12 subdomain. Perhatikan bahwa peringkat MPI (pengidentifikasi proses) mulai dari nol.
Perhatikan bahwa sumbu x dan y terbalik relatif terhadap penggunaan normal untuk mengasosiasikan sumbu x dengan baris dan sumbu y dengan kolom dari matriks solusi.
Untuk berkomunikasi antara proses yang berbeda, setiap proses harus mengetahui tetangganya. Ada perintah MPI yang sangat berguna yang melakukan ini secara otomatis dan disebut MPI_Cart_create . Sayangnya, shell Julia MPI tidak menyertakan perintah tingkat lanjut ini (dan menambahkannya sepertinya tidak sepele), jadi saya memutuskan untuk membuat fungsi yang melakukan tugas yang sama. Untuk membuatnya lebih ringkas, saya sering menggunakan operator ternary . Anda dapat menemukan fungsi ini di bawah.
Kode function neighbors(my_id::Int, nproc::Int, nx_domains::Int, ny_domains::Int) id_pos = Array{Int,2}(undef, nx_domains, ny_domains) for id = 0:nproc-1 n_row = (id+1) % nx_domains > 0 ? (id+1) % nx_domains : nx_domains n_col = ceil(Int, (id + 1) / nx_domains) if (id == my_id) global my_row = n_row global my_col = n_col end id_pos[n_row, n_col] = id end neighbor_N = my_row + 1 <= nx_domains ? my_row + 1 : -1 neighbor_S = my_row - 1 > 0 ? my_row - 1 : -1 neighbor_E = my_col + 1 <= ny_domains ? my_col + 1 : -1 neighbor_W = my_col - 1 > 0 ? my_col - 1 : -1 neighbors = Dict{String,Int}() neighbors["N"] = neighbor_N >= 0 ? id_pos[neighbor_N, my_col] : -1 neighbors["S"] = neighbor_S >= 0 ? id_pos[neighbor_S, my_col] : -1 neighbors["E"] = neighbor_E >= 0 ? id_pos[my_row, neighbor_E] : -1 neighbors["W"] = neighbor_W >= 0 ? id_pos[my_row, neighbor_W] : -1 return neighbors end
Kami melakukan hal yang sama ketika kami membangun labirin
Input ke fungsi ini adalah my_id , yang merupakan peringkat (atau pengidentifikasi) dari proses, jumlah proses nproc , jumlah divisi dalam arah x nx_domains dan jumlah divisi dalam arah y ny_domains .
Mari kita periksa fitur ini sekarang. Sebagai contoh, sekali lagi melihat ara. 5, kita dapat memeriksa output untuk proses peringkat 4 dan proses peringkat 11. Mari kita masuk ke REPL:
julia> neighbors(4, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 3 "W" => 1 "N" => 5 "E" => 7
dan
julia> neighbors(11, 12, 3, 4) Dict{String,Int64} with 4 entries: "S" => 10 "W" => 8 "N" => -1 "E" => -1
Seperti yang Anda lihat, saya menggunakan arah mata angin "N", "S", "E", "W" untuk menunjukkan lokasi tetangga. Misalnya, proses 4 memiliki proses 3 sebagai tetangga yang terletak di selatan posisinya. Anda dapat memverifikasi bahwa semua hasil di atas benar, mengingat bahwa "-1" dalam contoh kedua berarti bahwa tidak ada tetangga yang ditemukan di sisi "utara" dan "timur" proses 11.
5.2 Pesan
Seperti yang kita lihat sebelumnya, pada setiap iterasi, setiap proses mengirimkan perbatasannya ke proses tetangga. Pada saat yang sama, setiap proses menerima data dari tetangganya. Data ini disimpan oleh setiap proses dalam bentuk "sel hantu" dan digunakan untuk menghitung solusi di dekat batas setiap subdomain.
MPI memiliki perintah MPI_Sendrecv sangat berguna yang memungkinkan Anda untuk mengirim dan menerima pesan secara bersamaan antara dua proses. Sayangnya, MPI.jl tidak menyediakan fungsionalitas ini, namun masih mungkin untuk mencapai hasil yang sama menggunakan fungsi MPI_Send dan MPI_Receive secara terpisah.
Inilah yang telah dilakukan dalam fungsi updateBound! berikutnya updateBound! , yang memperbarui sel hantu di setiap iterasi. Input untuk fungsi ini adalah solusi 2D global u, yang mencakup sel hantu, serta semua informasi yang terkait dengan proses spesifik yang melakukan fungsi (berapa peringkatnya, apa koordinat subdomainnya, apa tetangganya). Fungsi pertama mengirim perbatasannya ke tetangga, dan kemudian menerima perbatasan mereka. Bagian penerima sedang diselesaikan melalui tim MPI.Waitall! , yang memastikan bahwa semua pesan yang diharapkan diterima sebelum memperbarui sel-sel samping untuk subdomain tertentu yang menarik.
Kode function updateBound!(u::Array{Float64,2}, size_total_x, size_total_y, neighbors, comm, me, xs, ys, xe, ye, xcell, ycell, nproc) mep1 = me + 1
5. Visualisasi solusi
Domain diinisialisasi dengan nilai konstan u = +10 sekitar batas, yang dapat diartikan sebagai keberadaan sumber suhu konstan pada batas. Kondisi awal u = −10 di dalam wilayah (Gbr. 6 di sebelah kiri). Seiring waktu, nilai u = 10 pada batas berdifusi ke pusat wilayah. Misalnya, pada langkah j = 15203 solusinya terlihat seperti yang ditunjukkan pada Gambar. 6 di sebelah kanan.
Dengan meningkatnya waktu t, solusinya menjadi lebih dan lebih homogen, sementara secara teoritis untuk itu tidak akan menjadi u = +10 seluruh domain.

Fig. 6. Kondisi awal (kiri) dan solusinya pada langkah 15203 dalam waktu (kanan). Batas-batas wilayah selalu disimpan di u = +10. Seiring waktu, solusinya menjadi semakin seragam dan cenderung menjadi semakin dekat dengan nilai u = +10 di seluruh wilayah.
6. Kinerja
Saya sangat terkesan ketika saya menguji kinerja implementasi Julia dibandingkan dengan Fortran dan C: Saya menemukan bahwa implementasi Julia adalah yang tercepat!
Sebelum mempelajari perbandingan, mari kita lihat kinerja MPI dari kode Julia itu sendiri. Gambar 7 menunjukkan rasio runtime ketika bekerja dengan proses 1 ke 2 (CPU). Idealnya, Anda ingin nomor ini mendekati 2, yaitu bekerja dengan dua prosesor harus dua kali lebih cepat dibandingkan dengan prosesor tunggal. Sebaliknya, diamati bahwa untuk ukuran tugas kecil (grid 128x128 sel), waktu kompilasi dan overhead komunikasi memiliki dampak negatif pada keseluruhan waktu eksekusi: akselerasi kurang dari satu. Keuntungan menggunakan banyak proses menjadi jelas hanya untuk tugas yang lebih besar.
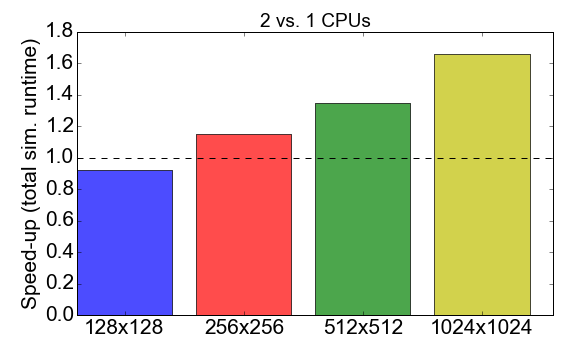
Gambar 7. Mempercepat implementasi Julia MPI dengan dua proses versus satu proses, tergantung pada kompleksitas tugas (ukuran kotak). "Akselerasi" mengacu pada rasio total waktu eksekusi menggunakan 1 proses untuk 2 proses.
Dan sekarang giliran yang tidak terduga: dalam gambar. Gambar 8 menunjukkan bahwa implementasi Julia lebih cepat dari Fortran dan C untuk tugas berukuran 256x256 dan 512x512 (hanya yang saya uji). Di sini saya hanya mengukur waktu yang diperlukan untuk menyelesaikan loop iterasi utama. Saya pikir ini adalah perbandingan yang adil, karena untuk simulasi yang panjang ini akan menjadi kontribusi terbesar untuk keseluruhan runtime.
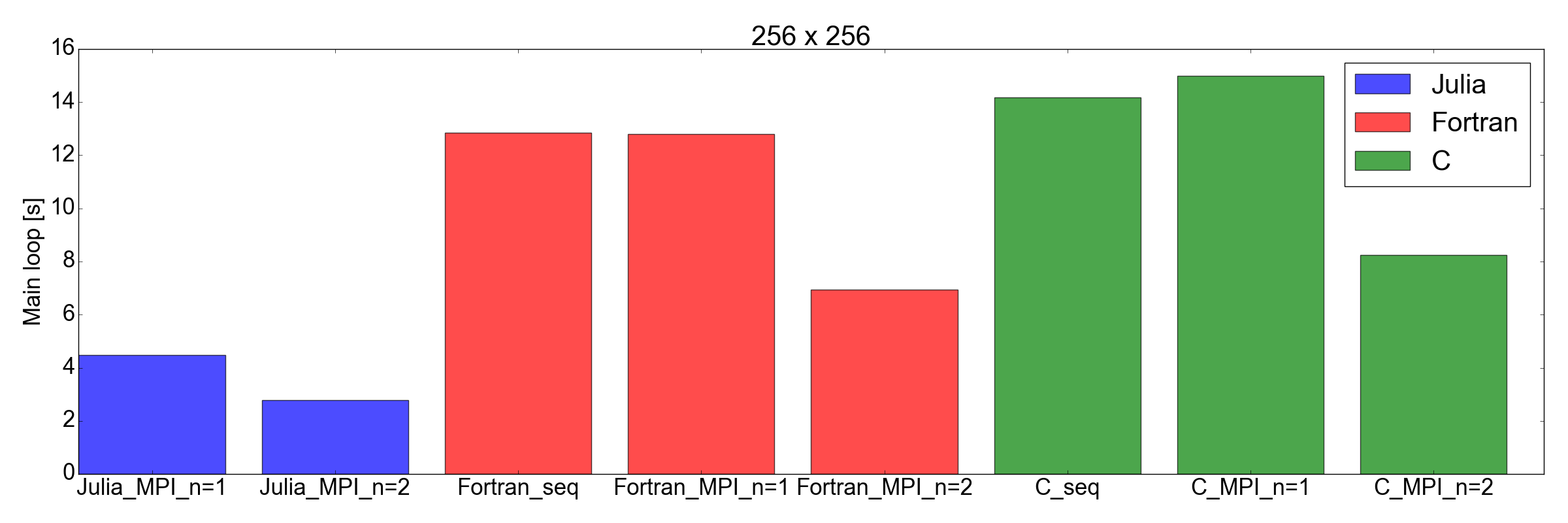

Gambar 8. Performa Julia vs Fortran vs C untuk dua ukuran kisi: 256x256 (atas) dan 512x512 (bawah). Ini menunjukkan bahwa Julia adalah bahasa dengan kinerja terbaik. Performa diukur sebagai waktu yang diperlukan untuk melakukan sejumlah iterasi pada loop kode utama.
Kesimpulan
Sebelum memulai posting ini, saya ragu Julia dapat bersaing dengan kecepatan Fortran dan C untuk aplikasi ilmiah. Alasan utamanya adalah karena saya sebelumnya telah menerjemahkan kode akademik yang berisi sekitar 2.000 baris dari Fortran ke Julia 0.6, dan saya melihat penurunan kinerja sekitar 3 kali.
Tapi kali ini ... Saya sangat terkesan. Saya sebenarnya baru menerjemahkan implementasi MPI yang ada ditulis dalam Fortran dan C ke Julia 1.0. Hasil ditunjukkan dalam gambar. 8, berbicara sendiri: Julia tampaknya yang tercepat sampai saat ini. Harap dicatat bahwa saya tidak memperhitungkan waktu kompilasi yang panjang yang dikonsumsi oleh kompiler Julia, karena ini akan menjadi faktor yang tidak signifikan untuk aplikasi "nyata" yang membutuhkan waktu berjam-jam untuk menyelesaikannya.
Saya juga harus menambahkan bahwa tes saya, tentu saja, tidak selengkap yang seharusnya untuk perbandingan menyeluruh. Bahkan, saya akan penasaran untuk melihat bagaimana kode bekerja dengan lebih dari dua prosesor (saya terbatas pada laptop pribadi di rumah saya) dan dengan peralatan lain (lihat Diffusion.jl ).
Bagaimanapun, latihan ini meyakinkan saya bahwa akan bernilai menghabiskan lebih banyak waktu mempelajari dan menggunakan Julia untuk Ilmu Data dan aplikasi ilmiah. Pergi ke prestasi baru!
Referensi