Geekly articles weekly

Bakat vs. Keberuntungan: Peran Kesempatan dalam Kesuksesan dan Kegagalan



Baru-baru ini, saya menemukan sebuah karya yang menarik oleh para ilmuwan Italia tentang peran keberuntungan dan peluang yang sangat diremehkan dalam kehidupan kita. Sayangnya, saya tidak menemukan versi lengkap dalam bahasa Rusia (mungkin saya terlihat buruk?), Tapi saya benar-benar ingin berbagi apa yang saya baca dengan teman-teman bahasa Inggris saya yang tidak lancar. Karena itu, sambil menyingsingkan lengan bajunya, ia mengatur terjemahan artisanalnya. Para penulis, Alessandro, Alessio dan Andrea, berbaik hati menerbitkannya di domain publik, jadi jika Anda tertarik, selamat datang di kucing.

Penulis


  • A. Pluchino - Departemen Fisika dan Astronomi, Universitas Catania dan Cabang Catania dari Institut Nasional Fisika Nuklir, Italia; alessandro.pluchino@ct.infn.it
  • A. E. Biondo - Departemen Ekonomi dan Bisnis, Universitas Catania, Italia; ae.biondo@unict.it
  • A. Rapisard - Departemen Fisika dan Astronomi, Universitas Catania dan Cabang Catania dari Institut Nasional Fisika Nuklir, Italia; Pusat Studi Sistem Kompleks, Wina; andrea.rapisarda@ct.infn.it


Anotasi


Untuk sebagian besar, posisi meritokratis yang dominan ( meritokrasi adalah prinsip tata kelola, di mana posisi orang-orang yang paling cakap, terlepas dari asal sosial dan kekayaan finansial mereka ) , model budaya Barat yang sangat kompetitif berasal dari kepercayaan bahwa kesuksesan terutama, jika tidak sepenuhnya, tergantung pada kualitas pribadi seperti bakat, kecerdasan, keterampilan, sumber daya, kerja keras, ketekunan, kerja keras atau pengambilan risiko. Terkadang kita siap mengakui bahwa sebagian keberuntungan juga dapat berperan dalam mencapai kesuksesan materi yang signifikan. Tetapi, sebenarnya, pentingnya kekuatan eksternal dalam kisah sukses individu sering diremehkan. Diketahui bahwa kecerdasan (atau, secara umum, bakat dan kualitas pribadi) dalam suatu populasi memiliki distribusi Gaussian, sedangkan distribusi nilai - sering dilihat sebagai ukuran keberhasilan - biasanya mengikuti hukum kekuasaan (hukum Pareto) ketika mayoritas miskin dan ada jumlah miliarder yang bisa diabaikan. Perbedaan antara input terdistribusi normal yang memiliki tingkat normal (rata-rata bakat atau kecerdasan) dan distribusi konstan pada output menunjukkan bahwa di suatu tempat di belakang layar ada komponen yang tidak terlihat. Dalam makalah ini, berdasarkan simulasi yang sangat sederhana dan berbasis agen mainan, kami membuat asumsi bahwa komponen seperti itu adalah kecelakaan biasa. Secara khusus, kami menunjukkan bahwa, meskipun kesuksesan hidup benar-benar membutuhkan sejumlah bakat, orang-orang paling berbakat hampir tidak pernah mencapai puncak kekayaan tertinggi, dikalahkan oleh orang-orang biasa-biasa saja, tetapi jauh lebih sukses. Sejauh yang kita tahu, hasil akal sehat yang bertentangan ini - meskipun secara implisit diasumsikan di antara banyak baris dalam literatur - adalah yang pertama memberikan penilaian kuantitatif. Hal ini memungkinkan Anda untuk melihat secara segar keefektifan mengevaluasi jasa berdasarkan tingkat keberhasilan yang telah dicapai dan menekankan risiko penyebaran penghargaan atau sumber daya yang berlebihan kepada orang-orang yang, dalam jangka panjang, mungkin lebih sukses daripada yang lain. Dengan menggunakan model ini, kami juga mempertimbangkan dan membandingkan beberapa hipotesis perilaku untuk menunjukkan strategi yang paling efektif untuk pendanaan penelitian publik, dengan tujuan meningkatkan meritokrasi, keanekaragaman dan inovasi.

1. Pendahuluan


Di mana-mana ketergantungan kekuasaan-hukum dalam banyak sistem kompleks fisik, biologis, atau sosial-ekonomi dapat dianggap sebagai sesuatu seperti fitur matematika yang khas dari hubungan dekat karakteristik dinamis mereka dengan struktur topologi yang tidak berubah [1, 2, 3, 4]. Dalam konteks sosial-ekonomi, menurut karya Pareto [5, 6, 7, 8, 9], diketahui bahwa distribusi kekayaan memiliki karakter hukum-kekuatan, yang bentuk memanjangnya yang khas mencerminkan kedalaman jurang yang ada antara orang kaya dan miskin di masyarakat kita.

Sebuah laporan baru-baru ini [10] menunjukkan bahwa saat ini kesenjangan ini jauh lebih besar daripada yang kita takutkan: delapan orang memiliki kekayaan yang sama dengan 3,6 miliar orang, yang merupakan bagian termiskin dari umat manusia. Selama 20 tahun terakhir, beberapa model teoritis telah dikembangkan yang menghitung distribusi nilai-nilai dalam konteks teori probabilitas dan statistik fisik, sering mengambil bentuk pemodelan multi-agen dengan dinamika internal yang sederhana [11, 12, 13, 14, 15, 16, 17].

Bergerak lebih jauh ke arah ini, jika kita menganggap kekayaan pribadi sebagai ukuran keberhasilan, dapat dikatakan bahwa distribusi yang sangat asimetris dan tidak setara di antara orang-orang adalah konsekuensi dari perbedaan alami mereka dalam bakat, keterampilan, kompetensi, kecerdasan, kemampuan atau ukuran dari ketekunan, kerja keras, atau tujuan. Asumsi semacam itu, dalam bentuk tersirat, adalah dasar dari apa yang disebut paradigma meritokratis: ia mempengaruhi tidak hanya bagaimana masyarakat kita menyediakan kesempatan kerja, kehormatan dan ketenaran, tetapi juga strategi yang diadopsi oleh pemerintah untuk mengalokasikan sumber daya dan keuangan kepada mereka yang dianggap paling kepribadian terhormat.

Namun, kesimpulan sebelumnya tampaknya sangat berbeda dari data yang dikonfirmasi bahwa properti dan kualitas orang yang disebutkan di atas biasanya didistribusikan ke seluruh populasi, yaitu, sesuai dengan distribusi Gaussian simetris relatif terhadap rata-rata ini. Misalnya, kecerdasan, yang diukur dengan tes IQ, sesuai dengan pola berikut: IQ rata-rata adalah 100, tetapi tidak ada yang memiliki IQ 1000 atau 10000. Hal yang sama berlaku untuk pekerjaan yang dihitung dalam jam kerja: seseorang bekerja lebih dari rata-rata, yang lain lebih sedikit, tetapi tidak ada orang yang bekerja satu miliar kali lebih banyak jam daripada yang lain.

Tetapi di zaman kita sekarang ini semakin banyak bukti mengenai peran mendasar dari kesempatan, keberuntungan, atau, secara umum, faktor-faktor acak, dalam menentukan keberhasilan atau kegagalan dalam urusan pribadi dan profesional kita. Secara khusus, ditunjukkan bahwa semua ilmuwan memiliki kesempatan yang sama untuk menerbitkan karya terobosan selama karir mereka [18]; bahwa mereka yang memiliki huruf pertama dari nama keluarga yang lebih dekat dengan awal alfabet jauh lebih mungkin untuk menerima posisi kepala departemen [19]; bahwa distribusi indikator bibliometrik yang dikumpulkan oleh para ilmuwan dapat berubah menjadi acak dan tidak berarti karena fenomena yang berkembang terkait dengan mekanisme inflasi "publikasikan atau matikan" [20]; bahwa posisi seseorang dalam daftar yang diurutkan berdasarkan abjad mungkin penting dalam menentukan akses ke layanan publik yang dibatasi oleh jumlah tempat [21]; bahwa huruf awal dari nama tengah meningkatkan penilaian kemampuan intelektual [22]; bahwa orang-orang dengan nama yang mudah diucapkan dinilai lebih positif daripada mereka yang namanya kompleks [23]; bahwa mereka yang namanya terdengar lebih aristokrat lebih sering daripada yang lain bekerja sebagai pemimpin dan bukan bawahan [24]; bahwa wanita dengan nama panggilan pria lebih sukses dalam profesi hukum [25]; bahwa sekitar setengah dari perbedaan pendapatan di antara orang-orang di seluruh dunia dijelaskan semata-mata oleh negara tempat tinggal mereka dan distribusi gaji di masing-masing negara [26]; bahwa kemungkinan menjadi direktur sangat dipengaruhi oleh nama dan bulan kelahiran Anda [27, 28, 29]; bahwa ide-ide inovatif adalah hasil dari reaksi acak dalam sel-sel otak kita [30]; dan bahkan kemungkinan mengembangkan kanker, sangat mungkin menghancurkan karier yang sangat baik, sebagian besar tergantung pada kegagalan [31, 32]. Karya terbaru tentang topik keberhasilan reproduksi sepanjang hidup berkontribusi pada konfirmasi pernyataan tersebut, menunjukkan bahwa jika penyimpangan sifat dapat mempengaruhi nasib populasi secara keseluruhan, maka kehidupan individu tertentu sering ditentukan oleh keberuntungan.

Dalam beberapa tahun terakhir, banyak penulis, termasuk ahli statistik dan analis risiko Nassim Taleb [35, 36], ahli strategi investasi Michael Mobussin [37] dan ekonom Robert Frank [38], telah menyelidiki dalam sejumlah buku populer hubungan antara keberuntungan dan keterampilan dalam transaksi keuangan. bisnis, olahraga, seni, musik, sastra, sains, dan banyak bidang lainnya. Mereka menyimpulkan bahwa peristiwa acak memainkan peran yang jauh lebih besar dalam kehidupan daripada yang dibayangkan banyak orang. Kenyataannya, mereka tidak berasumsi bahwa kesuksesan tidak bergantung pada talenta dan upaya, karena dalam bidang atau pasar yang sangat kompetitif seperti "pemenang mengambil segalanya", di mana kita hidup dan bekerja saat ini, orang yang paling produktif hampir selalu luar biasa berbakat dan pekerja keras. Mereka hanya menyimpulkan bahwa bakat dan usaha tidak cukup: Anda juga harus berada di tempat yang tepat pada waktu yang tepat. Singkatnya, keberuntungan juga mempengaruhi, meskipun perannya hampir selalu diremehkan oleh orang-orang sukses. Hal ini disebabkan oleh fakta bahwa keacakan sering bekerja dengan cara yang tidak jelas, sehingga mudah untuk membandingkan peristiwa yang menunjukkan keberhasilan sebagai sesuatu yang tidak bisa dihindari. Taleb menyebut kecenderungan semacam itu "kekeliruan yang fantastis" [36], dan sosiolog Paul Lazarsfeld mengusulkan istilah "bias retrospektif". Dalam buku terakhirnya, "Semuanya Jelas: Ketika Anda Tahu Jawabannya" [39], sosiolog dan perintis ilmu jaringan Duncan Watts menunjukkan bahwa baik khayalan luar biasa dan bias retrospektif bias terhadap fenomena khusus di mana orang-orang yang melihat hasil yang luar biasa sukses, menganggap mereka sebagai produk kerja keras dan bakat yang tidak diragukan. Namun, kesuksesan terutama muncul melalui langkah-langkah yang rumit dan saling terkait, yang masing-masing tergantung pada yang sebelumnya: jika ada di antara mereka yang berbeda, seluruh karier atau jalan hidup hampir pasti juga akan berbeda. Argumen ini juga didasarkan pada hasil penelitian eksperimental yang inovatif yang dilakukan beberapa tahun sebelumnya oleh Watts sendiri dalam kolaborasi dengan penulis lain [40], di mana keberhasilan lagu-lagu yang sebelumnya tidak dikenal di pasar musik buatan tidak terbukti berkorelasi dengan kualitas karya itu sendiri. Dan ini, tentu saja, sangat menyulitkan prediksi apa pun, seperti yang ditunjukkan dalam penelitian lain yang lebih baru [41].

Dalam tulisan ini, menggunakan pendekatan statistik berbasis agen, kami akan mencoba untuk secara praktis menentukan peran keberuntungan dan bakat dalam karier yang sukses. Dalam Bagian 2, berdasarkan jumlah minimum asumsi, yaitu, sifat Gaussian dari distribusi bakat [42] dan dinamika multiplikasi dari keberhasilan dan kegagalan [43], kami menyajikan model sederhana, yang kami sebut model "Talent vs. Luck" (TPU), di yang meniru pengembangan karir profesional sekelompok orang selama 40 tahun masa kerja mereka. Model ini menunjukkan bahwa dalam kenyataannya, keacakan memainkan peran mendasar dalam menentukan individu yang paling sukses. Yang benar adalah bahwa, seperti yang diduga, orang-orang berbakat lebih cenderung menjadi kaya, terkenal atau signifikan dalam kehidupan mereka sendiri, dalam kaitannya dengan orang-orang yang kurang siap. Tetapi, dan penjelasan yang kurang intuitif ini, orang-orang biasa dengan tingkat bakat yang biasa secara statistik ditakdirkan untuk menjadi sukses (mis., Untuk ditempatkan di akhir distribusi kekuatan yang sukses) jauh lebih sering daripada yang paling berbakat, asalkan mereka menjadi favorit bagi keberuntungan. hidupmu. Fakta ini sering ditemui, seperti yang ditunjukkan dalam referensi [35, 36, 38], tetapi, sejauh yang kami tahu, ini pertama kali dimodelkan dan diukur dalam karya ini.

Keberhasilan orang-orang dengan bakat biasa mempertanyakan paradigma "meritokratis" dan semua strategi dan mekanisme yang memberi lebih banyak penghargaan, peluang, kehormatan, ketenaran, dan sumber daya bagi orang-orang yang dianggap terbaik di bidangnya [44, 45]. Faktanya adalah bahwa, dalam sebagian besar kasus, semua penilaian bakat seseorang diberikan setelah fakta, semata-mata dengan melihat aktivitasnya, atau hasil yang dicapai, di area spesifik masyarakat kita, seperti olahraga, bisnis, keuangan, seni , sains, dll. Jenis penilaian menyesatkan mengarah pada substitusi sebab dan akibat, mengevaluasi sebagai orang yang paling berbakat, mereka yang, paling sederhana, yang paling sukses [46, 47]. Sesuai dengan pandangan ini, karya-karya sebelumnya memperingatkan jenis serupa "meritokrasi dekat" dan menunjukkan efektivitas strategi lain berdasarkan sampel acak di banyak lingkungan yang berbeda, seperti manajemen, politik dan keuangan [48, 49, 50, 51, 52, 53, 54, 55]. Pada Bagian 3, kami menerapkan pendekatan dan garis besar bagaimana distribusi dana publik dimungkinkan dalam konteks penelitian ilmiah. Kami mempelajari konsekuensi dari berbagai strategi distribusi, di antaranya ada strategi meritokratik "dekat", dengan tujuan mengeksplorasi cara-cara baru untuk meningkatkan, pada saat yang sama, tingkat keberhasilan minimum orang-orang paling berbakat di masyarakat dan efektivitas total pengeluaran pemerintah. Kami juga akan memeriksa, secara umum, bagaimana peluang yang ditawarkan oleh lingkungan, disajikan dalam bentuk tingkat pendidikan dan pendapatan (mis., Faktor eksternal tergantung pada negara dan lapisan sosial dari mana orang berasal), penting dalam meningkatkan kemungkinan keberhasilan. Komentar akhir menyelesaikan pekerjaan.

2. Model


Selanjutnya, kami mengusulkan model agen yang disebut "Talent versus Good Luck" (TPU), berdasarkan sejumlah kecil asumsi, dan bertujuan untuk menggambarkan evolusi karier sekelompok orang di bawah pengaruh peristiwa sukses dan tidak berhasil yang terjadi secara acak.


Gambar 1: Contoh parameter awal untuk simulasi kami. Semua simulasi yang disajikan dalam makalah ini dilakukan dalam lingkungan simulasi agen NetLogo [56]. N = 1000 orang (agen), dengan berbagai tingkat bakat (kecerdasan, keterampilan, dll.) Didistribusikan secara acak pada posisi tetap dalam dunia persegi bagian 201 × 201 dengan kondisi batas siklik. Selama setiap simulasi, yang berlangsung selama beberapa dekade, mereka terpapar pada sejumlah N N sukses (lingkaran hijau) dan tidak berhasil (lingkaran merah) yang bergerak di seluruh dunia sepanjang lintasan acak (random walk). Dalam contoh ini, N E = 500.

Kami menganggap N individu dengan talenta (intelek, keterampilan, kemampuan, dll.) Memiliki distribusi normal dalam interval [0; 1] sekitar rata-rata m T dengan deviasi standar σ T ditempatkan secara acak pada posisi tetap dalam dunia kuadrat (lihat Gambar 1) dengan kondisi batas siklik (yaitu, dengan topologi toroidal) dan dikelilingi oleh sejumlah N E "bergerak" peristiwa (ditandai dengan titik-titik), beberapa di antaranya berhasil, tidak ada yang lain (peristiwa netral dalam model ini tidak diperhitungkan, karena tidak memiliki konsekuensi signifikan pada kehidupan individu). Dalam Gambar 1, kami menunjukkan peristiwa ini dalam bentuk titik-titik berwarna: berhasil dalam warna hijau dan dengan persentase relatif pL, dan tidak berhasil dalam warna merah dan dengan persentase ( 100 - pL ). Jumlah total titik acara N E terdistribusi secara merata, tetapi, tentu saja, distribusi seperti itu idealnya hanya seragam untuk N E → ∞ . Dalam simulasi kami, biasanya akan ada N E ≈ N / 2 , oleh karena itu, pada awal setiap simulasi, ada konsentrasi acak yang signifikan dari poin acara yang berhasil atau tidak berhasil di berbagai wilayah di dunia, sementara wilayah lain akan lebih netral. Pergerakan titik-titik acak berikutnya di dalam matriks kuadrat, yaitu, dunia, tidak mengubah fitur mendasar dari model ini, yang menunjukkan sejumlah peristiwa keberhasilan atau kegagalan yang berbeda untuk orang yang berbeda sepanjang hidup mereka, terlepas dari bakat pribadi mereka.


Gambar 2: distribusi talenta normal di antara populasi (dengan median m T = 0,6 ditunjukkan oleh garis vertikal putus-putus dan standar deviasi σ T = 0,1 - nilai-nilai m T ± σ T ditampilkan sebagai dua garis vertikal bertitik). Distribusi ini dialokasikan dalam interval [0; 1] dan tidak berubah selama simulasi.

Satu simulasi menjalankan menguji masa kerja P 40 tahun (usia dua puluh hingga enam puluh tahun), dengan langkah waktu enam bulan. Pada awal simulasi, semua agen diberi modal yang sama C i = C (0) Ɐ i = 1, ..., N , mewakili tingkat awal kesuksesan / kesejahteraan mereka. Pilihan ini memiliki tujuan yang jelas untuk tidak memberi siapa pun keuntungan awal. Sementara talenta agen tidak tergantung waktu, modal mereka berubah. Selama pengembangan model ini, mis., Selama periode yang diharapkan dari kehidupan agen, semua titik peristiwa bergerak secara acak di seluruh dunia dan, pada saat yang sama, dapat bersinggungan dengan lokasi beberapa agen. Jika Anda masuk ke detail, setiap kali setiap titik acara mencakup, dalam arah acak, jarak 2 bagian. Kami percaya bahwa ada persimpangan dengan individu jika titik peristiwa yang diwakili di dalam lingkaran dengan jari-jari satu segmen berpusat pada agen (titik acara tidak hilang setelah persimpangan).Bergantung pada insiden seperti itu, pada langkah ini t (yaitu, setiap enam bulan), dengan agen tertentu A k , tiga opsi berikut ini dimungkinkan:

  1. Tidak ada titik peristiwa yang melintasi posisi agen A k - ini berarti bahwa selama enam bulan terakhir tidak ada peristiwa seperti itu terjadi, agen A k tidak melakukan tindakan apa pun.
  2. A k – , ( , [30], , ); , A k / , T k . C k (t) = 2C k (t − 1) , rand[0; 1] < T k , .., , .
  3. A k – , ; , A k / , .. C k (t) = C k (t − 1) / 2 .


Aturan untuk agen di atas (termasuk pilihan untuk membagi modal awal menjadi setengah dalam hal peristiwa yang tidak berhasil dan menggandakan dalam kasus yang sukses, sebanding dengan bakat agen) sengaja sederhana dan dapat dianggap luas, karena mereka didasarkan pada fakta yang jelas bahwa kesuksesan dalam kehidupan sehari-hari adalah milik keduanya tumbuh dan menurun dengan cepat. Selain itu, aturan-aturan ini memberikan keuntungan yang signifikan bagi orang-orang yang sangat berbakat, karena mereka dapat memperoleh manfaat lebih dari peluang yang disajikan oleh keberuntungan (termasuk kemampuan untuk menggunakan ide bagus yang berasal dari otak mereka). Di sisi lain, misalnya, kecelakaan mobil atau sakit mendadak, selalu merupakan peristiwa yang tidak berhasil di mana bakat tidak menjadi masalah. Dalam hal ini, kita dapat memperoleh definisi "bakat" yang lebih akurat,mendefinisikannya sebagai "kualitas pribadi apa pun yang meningkatkan peluang untuk meraih peluang." Dengan kata lain, dengan istilah "talenta" kita, dalam arti luas, berarti kecerdasan, keterampilan, sumber daya, keuletan, tekad, kerja keras, pengambilan risiko, dan sebagainya. Lebih jauh kita akan melihat bahwa keuntungan dari memiliki talenta hebat adalah syarat yang diperlukan tetapi tidak cukup untuk mencapai puncak kesuksesan yang sangat tinggi.

2.1. Hasil sekali jalan


Dalam subbab ini kami menyajikan hasil dari satu simulasi yang khas. Secara umum, hasil ini cukup stabil, oleh karena itu, seperti yang kami tunjukkan di bawah, hasilnya dapat secara substansial mewakili kerangka umum yang meninggalkan model kami.

Mari kita bayangkan N = 1000 agen dengan jumlah modal benih yang sama C (0) = 10 (dalam satuan abstrak) dan dengan talenta tetap T i ϵ [0; 1], distribusi normal berikut dengan median m T = 0,6 dan standar deviasi σ T = 0,1 (lihat Gambar 2). Seperti disebutkan sebelumnya, simulasi mencakup rentang waktu realistis P= 40 tahun, berkembang dalam langkah yang sama, masing-masing enam bulan, total dari I = 80 iterasi. Dalam simulasi ini, kami mengambil N E = 500 poin acara, dengan probabilitas kejadian yang berhasil p L = 50%.

Pada akhir simulasi, seperti yang dapat dilihat dari skema (a) pada Gambar 3, kami menemukan bahwa aturan model dinamis sederhana dapat menghasilkan distribusi modal / keberhasilan yang tidak merata, dengan sejumlah besar agen yang miskin (tidak berhasil) dan sejumlah kecil agen yang sangat kaya (sukses). Setelah membangun distribusi yang sama pada skala bilogaritmik, dalam skema (b) dari gambar yang sama kita melihat distribusi sesuai dengan fungsi daya dalam gaya Pareto, kemiringan yang sesuai dengan fungsi y © ≈ C −1.27 .

Dengan demikian, terlepas dari distribusi talenta yang normal, model TPU tampaknya mampu menangkap fitur penting pertama yang diamati bila dibandingkan dengan data nyata: kesenjangan terdalam antara kaya dan miskin dan sifat skalanya yang berubah-ubah. Secara khusus, dalam simulasi kami hanya 4 orang yang menerima lebih dari 500 unit modal, dan 20 orang paling sukses memiliki 44% dari semua nilai, sementara hampir setengah dari populasi memiliki kurang dari 10 unit. Secara umum, aturan Pareto "80/20" diamati, karena 80% dari populasi hanya memiliki 20% dari total modal, sementara 20% individu yang tersisa memiliki 80% kekayaan. Meskipun ketidaksetaraan ini nampaknya tidak adil, itu akan agak dapat diterima jika sebagian besar orang-orang sukses adalah di antara yang paling berbakat,dengan demikian menghasilkan lebih banyak akumulasi modal / sukses daripada yang lain. Tetapi apakah ini benar-benar terjadi?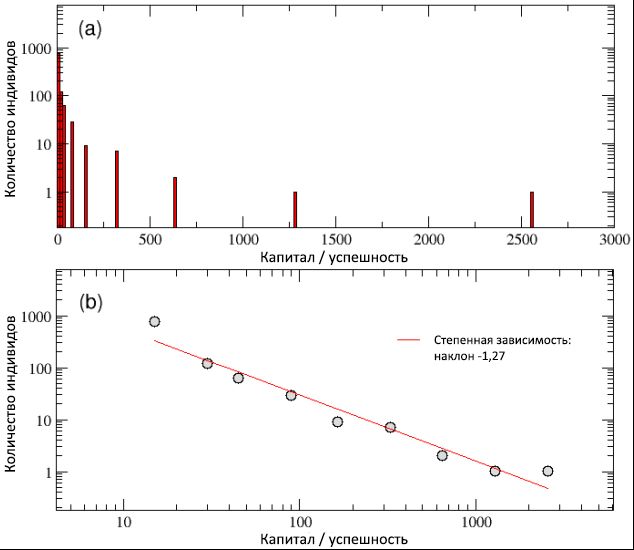


Gambar 3: Distribusi akhir kekayaan / kesuksesan di antara populasi, pada skala linier logaritmik (a) dan bilogaritmik (b). Meskipun distribusi bakat normal, ekor dari distribusi keberhasilan, seperti yang dapat dilihat dari skema (b), dapat digambarkan sebagai kurva daya dengan kemiringan .21,27. Kami juga telah mengkonfirmasi bahwa distribusi modal / sukses mengikuti undang-undang Pareto "80/20", karena 20% populasi memiliki 80% dari nilai dan sebaliknya.

Pada Gambar. 4, skema (a) dan (b), masing-masing, bakat ditampilkan sebagai fungsi dari total modal / keberhasilan, dan sebaliknya (perhatikan bahwa dalam skema (a) modal / sukses hanya memiliki nilai diskrit - ini terkait dengan keputusan gunakan modal awal yang sama untuk semua agen). Pandangan kedua skema menunjukkan bahwa, di satu sisi, individu yang paling sukses bukanlah yang paling berbakat dan, sebaliknya, individu yang paling berbakat bukanlah yang paling sukses. Secara khusus, paling individu yang sukses, dengan C max = 2560, memiliki bakat T * = 0,61, yang hanya sedikit di atas nilai median m T = 0,6, sementara sebagian besar berbakat ( T max= 0,89) memiliki modal / tingkat keberhasilan kurang dari 1 unit ( C = 0,625).

Seperti yang kita pelajari secara lebih rinci dari subbagian berikutnya, hasil seperti itu bukan kasus khusus, melainkan aturan untuk sistem jenis ini: keberhasilan maksimum tidak pernah menyatu dengan bakat maksimum, dan sebaliknya. Selain itu, perbedaan antara kesuksesan dan bakat ini tidak proporsional dan sangat tidak linier. Bahkan, modal rata-rata semua orang dengan bakat T> T * adalah C≈ 20; dengan kata lain, modal / kesuksesan orang paling sukses dengan bakat sedang adalah 128 kali lebih tinggi daripada modal rata-rata / kesuksesan orang yang jauh lebih berbakat daripada yang pertama. Kita dapat menyimpulkan bahwa jika bakat luar biasa tidak tersembunyi di balik alasan kesuksesan luar biasa dari beberapa orang, maka, mungkin, ada faktor lain. Simulasi kami dengan jelas menunjukkan bahwa keberuntungan murni adalah faktor semacam itu.


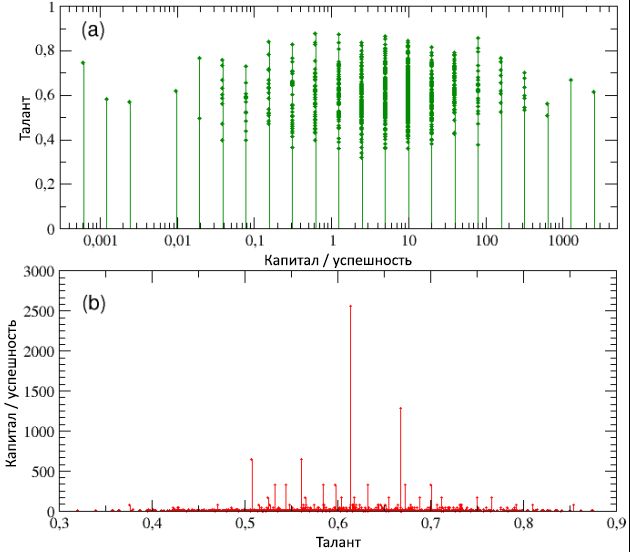Gambar 4: dalam diagram (a), bakat ditampilkan sebagai fungsi modal / sukses (pada skala logaritmik, untuk visualisasi yang lebih baik) - ini menunjukkan bahwa individu yang paling sukses bukanlah, pada saat yang sama, yang paling berbakat. Dalam diagram (b), sebaliknya, ibukota / keberhasilan ditampilkan sebagai fungsi dari bakat - maka Anda lebih baik dapat menghargai fakta bahwa agen sukses yang paling dengan C max= 2560, memiliki bakat yang hanya sedikit melebihi nilai median m T = 0,6, sedangkan yang paling berbakat memiliki modal / sukses lebih rendah dari C = 1 unit, jauh lebih sedikit dari modal awal C (0). Baca terus untuk detail lebih lanjut.

Pada Gambar 5, jumlah peristiwa sukses dan tidak berhasil yang terjadi dengan semua orang selama periode kehidupan kerja mereka ditampilkan sebagai fungsi dari total modal / kesuksesan mereka. Ketika mempertimbangkan skema (a), menjadi jelas bahwa individu yang paling sukses pada saat yang sama adalah yang paling sukses (perhatikan bahwa diagram ini menunjukkan semua peristiwa sukses yang terjadi pada agen, dan bukan hanya dari mana mereka dapat memperoleh manfaat, sesuai dengan dengan bakatmu). Sebaliknya, ketika melihat skema (b), kita melihat bahwa yang paling gagal pada saat yang sama adalah yang paling tidak berhasil. Dengan kata lain, meskipun tidak ada korelasi antara kesuksesan dan bakat, berdasarkan simulasi, ada ketergantungan yang kuat terhadap keberuntungan. Menganalisis detail distribusi frekuensi dari jumlah peristiwa yang berhasil dan tidak berhasil yang terjadi dengan individu, kami temukanseperti yang ditunjukkan dalam diagram © dan (d) bahwa kedua nilai ini adalah eksponensial, dengan derajat 0,64 dan 0,48, dan median masing-masing 1,35 dan 1,66, dan bahwa jumlah maksimum peristiwa sukses dan tidak berhasil terjadi, masing-masing, 10 dan 15. Selain itu, sekitar 16% memiliki kehidupan "netral", umumnya tanpa peristiwa yang berhasil dan tidak berhasil, sementara 40% individu hanya mengalami satu jenis peristiwa (sukses atau tidak berhasil).sementara 40% individu hanya mengalami satu jenis acara (sukses atau tidak berhasil).sementara 40% individu hanya mengalami satu jenis acara (sukses atau tidak berhasil).

Menarik juga untuk melihat periode perkembangan kesuksesan / modal baik untuk individu yang paling sukses maupun yang tidak berhasil, dibandingkan dengan urutan yang sesuai dari peristiwa yang berhasil dan tidak berhasil yang terjadi selama 40 tahun (80 interval, 6 bulan masing-masing) dari kehidupan kerja mereka. Hasilnya dapat dilihat, masing-masing, di bagian kiri dan kanan dari Gambar 6. Tidak seperti skema (a) dari gambar 5, skema yang lebih rendah dari gambar ini hanya berisi peristiwa-peristiwa yang berhasil di mana agen, berkat bakat mereka, dapat memperoleh manfaat.


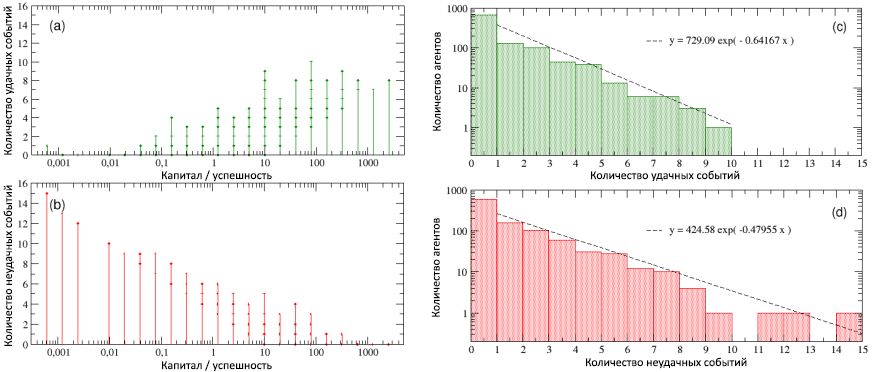Gambar 5: jumlah total peristiwa yang berhasil (a) dan tidak berhasil (b), sebagai fungsi dari modal / keberhasilan agen. Grafik menunjukkan korelasi yang kuat antara kesuksesan dan kesuksesan: individu yang paling sukses juga yang paling sukses, dan sebaliknya. Sekali lagi, karena penggunaan modal awal yang sama untuk semua agen, ternyata sejumlah peristiwa dikelompokkan ke dalam nilai-nilai diskrit modal / kesuksesan. Dalam diagram © dan (d), frekuensi distribusi, masing-masing, dari jumlah peristiwa yang berhasil dan tidak berhasil ditampilkan pada skala log-linear. Seperti yang dapat dilihat, kedua distribusi dapat ditulis dalam bentuk ketergantungan eksponensial dengan kekuatan negatif yang sama).

Dalam diagram (atas dan bawah) (a) pada Gambar 6, mengenai individu yang cukup berbakat tetapi paling sukses, terlihat jelas bahwa setelah sekitar setengah dari kehidupan kerjanya, disertai dengan manifestasi langka dari peristiwa sukses (diagram bawah), dan tingkat modal yang rendah (atas skema), konsentrasi tiba-tiba peristiwa menguntungkan yang terjadi antara 30 dan 40 langkah waktu (mis., tepat sebelum ulang tahun ke-40 agen) menyebabkan peningkatan pesat dalam modal, yang dalam 10 langkah terakhir (mis., dalam 5 tahun terakhir karier agen) ) menjadi eksponensial dengan pergi dari C = 320 hingga C maks = 2560.

Di sisi lain, dengan melihat diagram (atas dan bawah) (b) dari gambar yang sama mengenai individu yang paling tidak berhasil, menjadi jelas bahwa paruh kedua kehidupan kerjanya yang tidak berhasil, disertai dengan selusin peristiwa buruk, terus berkurang modal / sukses, mengarah ke final nilai C = 0,00061. Sangat menarik untuk dicatat bahwa bakat agen yang malang ini adalah T= 0,74, yang lebih tinggi dari sebagian besar yang paling sukses. Jelas, menciptakan perbedaan dipengaruhi oleh keberuntungan. Dan jika memang benar bahwa agen yang paling sukses layak mendapatkan keuntungan dari semua peluang yang diberikan kepadanya (terlepas dari bakatnya yang biasa-biasa saja), juga benar bahwa jika hidup Anda penuh dengan kemalangan dan tidak memberikan peluang, seperti agen kedua ini, maka bahkan talenta terhebat menjadi tidak berdaya melawan kegagalan kekerasan.


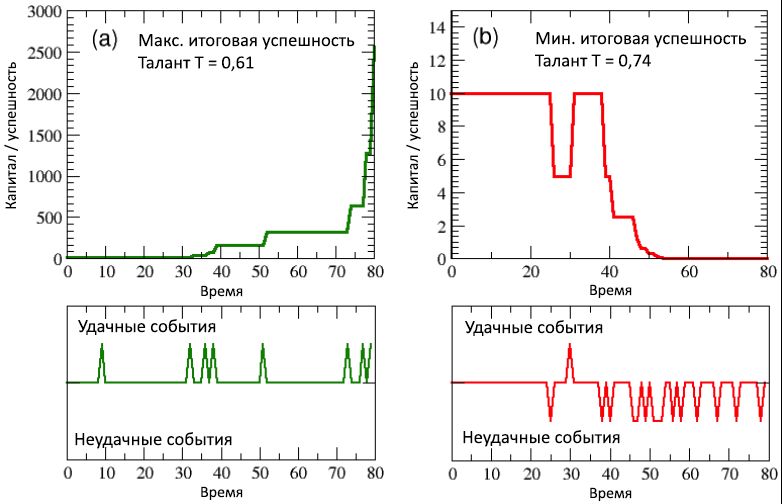Gambar 6: (a) periode pengembangan keberhasilan / modal individu paling sukses dan (b) paling disayangkan, dibandingkan menurut urutan yang sesuai dari peristiwa sukses dan tidak berhasil yang terjadi selama kehidupan kerja mereka (dari 80 setengah tahun, yaitu, 40 tahun). Waktu terjadinya peristiwa tersebut dicatat dalam diagram yang lebih rendah dalam bentuk puncak naik dan turun.

Semua hasil dari satu putaran (versi demo dari kode NetLogo dari model TPU yang digunakan untuk simulasi ini dapat ditemukan dalam repositori Open ABM) yang disajikan dalam subbagian ini sangat stabil dan, seperti yang akan kita lihat dari subbab berikutnya, mereka diselamatkan, dengan sedikit perbedaan, dengan banyak pengulangan simulasi dimulai dengan distribusi bakat yang sama, tetapi dengan posisi acak individu yang berbeda.

2.2. Hasil Jalankan Berganda


Dalam ayat ini, kami menyajikan hasil simulasi umum dari rata-rata lebih dari 100 kali, masing-masing dimulai dengan kondisi awal yang berbeda, dipilih secara acak. Nilai-nilai parameter kontrol adalah sama seperti pada ayat sebelumnya: N = 1000 individu, m T = 0,6 dan σ T = 0,1 untuk distribusi talenta yang normal, I = 80 iterasi (masing-masing mewakili δ t = 6 bulan masa kerja ), C (0) = 10 unit modal awal, N E = 500 poin acara dan persentase kejadian yang berhasil p L = 50%.

Dalam diagram (a) dari Gambar 7, distribusi total modal total / keberhasilan di antara semua agen yang dikumpulkan sebagai hasil dari 100 run ditunjukkan pada skala logaritmik dan dijelaskan dengan baik oleh kurva hukum-kekuatan dengan koefisien sudut −1,33. Properti dari keteguhan modal yang diamati dalam satu putaran terlepas dari skala dan menghasilkan ketidaksetaraan yang tinggi di antara individu, serta aturan Pareto “80/20”, dengan demikian dipertahankan dalam kasus beberapa putaran. Bahkan, kesenjangan antara agen kaya (sukses) dan miskin (tidak berhasil) bahkan melebar, karena modal orang terkaya kini telah melampaui 40.000 unit.

Hasil ini dapat diperkirakan dengan melihat skema (b) dari Gambar 7, di mana total modal Cmax hanya individu yang paling sukses ditampilkan sebagai fungsi bakat menunjukkan hasil terbaik di masing-masing 100 berjalan. Agen dengan talenta T terbaik = 0,6048, hampir bertepatan dengan median distribusi talenta ( m T = 0,6), yang mencapai puncak modal C terbaik = 40960, menerima poin terbanyak. Di sisi lain, individu yang paling berbakat dari individu paling sukses, dengan talent Tmax = 0,91, mendapatkan modal Cmax = 2560, yang hanya 6% dari C terbaik .


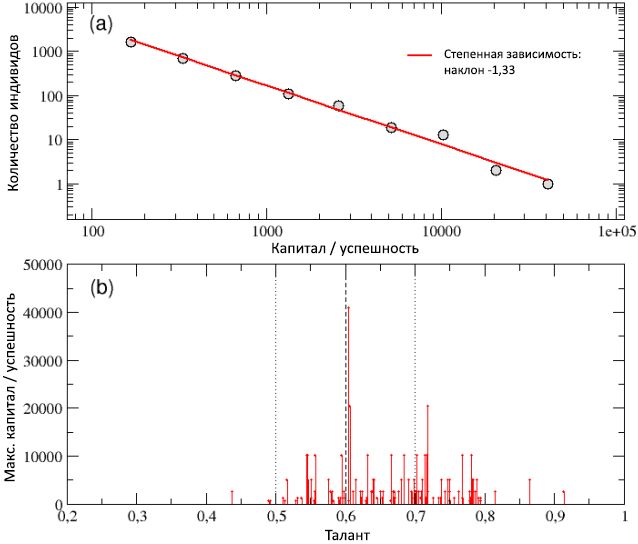
Gambar 7: Skema (a) - distribusi total modal / keberhasilan yang dihitung lebih dari 100 berjalan untuk populasi dengan kondisi awal yang ditentukan secara acak berbeda. Distribusi dapat digambarkan oleh kurva daya dengan kemiringan −1.33. Skema (b) - total modal Cmax dari individu paling sukses dalam masing-masing 100 berjalan, ditampilkan sebagai fungsi dari bakat mereka. Rata-rata orang yang memiliki bakat cukup tinggi lebih berhasil daripada mereka yang memiliki bakat rendah atau sedang, dan paling sering individu yang paling sukses adalah agen yang cukup berbakat, dan hanya kadang-kadang yang paling berbakat. Nilai mT , serta nilai mT ± σ T , masing-masing ditunjukkan dalam bentuk garis putus-putus vertikal dan garis putus-putus.

Untuk mempertimbangkan sudut pandang ini secara lebih rinci, pada Gambar 8 (a) kami merencanakan distribusi talenta dengan kinerja terbaik, yang dihitung untuk 100 run. Distribusi, jelas, bergeser ke kanan di sepanjang poros bakat, dengan nilai rata-rata Tv = 0,66> m T - ini menegaskan, di satu sisi, bahwa untuk mencapai kesuksesan yang signifikan, bakat yang cukup tinggi sering diperlukan; namun, di sisi lain, ini juga menunjukkan bahwa kondisi ini hampir tidak pernah cukup, karena agen dengan talenta tertinggi (mis., dengan T > m T = 2σ T , atau T > 0.8) adalah di antara yang berkinerja terbaik saja. dalam 3% kasus, dan modal / keberhasilan mereka tidak pernah melebihi 13% dari C terbaik .


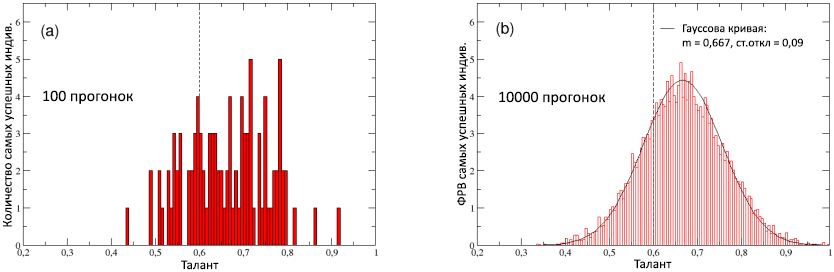
Gambar 8: (a) Distribusi talenta dari kepribadian paling sukses (berkinerja terbaik) di masing-masing 100 run. (B) Fungsi distribusi probabilitas (RFF) dari bakat individu yang paling sukses, dihitung dalam 10.000 berjalan: dijelaskan dengan baik oleh distribusi normal dengan median 0,667 dan standar deviasi 0,09 (kurva padat). Sebagai perbandingan, median m T = 0,6 dari distribusi bakat normal awal dalam populasi ditampilkan, ditunjukkan dalam kedua skema dengan garis vertikal putus-putus.

Dalam diagram (b) dari Gambar 8, distribusi yang sama (dikurangi menjadi total area untuk mendapatkan FRF) dihitung untuk 10.000 run untuk memahami bentuk aslinya: sepertinya cocok dengan kurva Gaussian G (T) dengan rata-rata T av = 0,667 dan standar deviasi 0,09 (garis solid). Ini, tentu saja, menegaskan bahwa distribusi talenta berkinerja terbaik digeser ke kanan relatif terhadap poros talenta, dibandingkan dengan distribusi awal. Untuk lebih tepatnya, ini berarti bahwa probabilitas bersyarat P ( Cmax | T ) = G (T) dT untuk menemukan di antara yang berkinerja terbaik memiliki kepribadian dengan bakat dalam interval [ T ; T + dT ] tumbuh dengan talenta T , memuncak dekat talenta sedang-sedang Tv = 0,66, dan kemudian turun tajam dengan nilai talenta besar. Dengan kata lain, probabilitas menemukan individu yang cukup berbakat di atas kesuksesan lebih tinggi daripada menemukan individu yang sangat berbakat di sana. Perhatikan bahwa dalam dunia ideal di mana bakat adalah alasan utama untuk sukses, diharapkan bahwa P ( Cmax | T ) akan menjadi fungsi yang berkembang dari T. Dengan demikian, kita dapat menyimpulkan bahwa bentuk Gaussian yang diamati P ( Cmax | T ) adalah bukti dari pentingnya keberuntungan yang lebih besar daripada bakat dalam mencapai tingkat kesuksesan yang sangat tinggi.


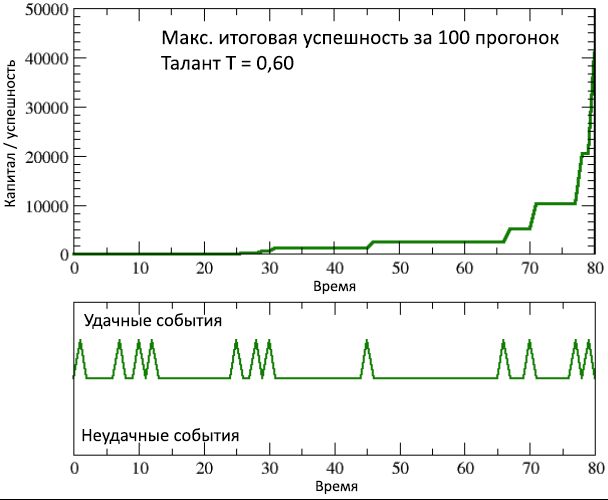
Gambar 9: perubahan waktu keberhasilan / modal orang paling sukses (tetapi pada saat yang sama, cukup berbakat), dari 100 simulasi berjalan, dibandingkan dengan urutan yang tidak biasa terkait peristiwa sukses yang terjadi dalam hidupnya.

Menarik juga untuk membandingkan, dari 100 kali berjalan, rata-rata modal / tingkat keberhasilan C mt ≈ 63 dari orang paling berbakat dengan rata-rata C yang sesuai pada ≈ 33 dari mereka yang bakatnya dekat dengan median m T. Dalam kedua kasus, kami menemukan indikator yang agak rendah (bahkan jika lebih dari modal awal C (0) = 10), tetapi fakta bahwa C mt > C at menunjukkan bahwa meskipun kemungkinan menemukan individu yang cukup berbakat di puncak kesuksesan lebih tinggi, daripada orang yang sangat berbakat, individu-individu paling berbakat dari setiap lari, rata-rata, lebih sukses daripada orang-orang yang berbakat. Di sisi lain, melihat rata-rata lebih dari 100 berjalan, proporsi individu dengan bakat T > 0,7 (yaitu lebih tinggi daripada dengan standar deviasi dari median) dan keberhasilan akhir / modal C > 10, dihitung dengan mempertimbangkan semua agen dengan talenta T > 0,7 (yang, rata-rata untuk setiap putaran, ≈ 160), kami menemukan bahwa bagian ini adalah 32% - ini berarti bahwa kinerja gabungan dari orang-orang paling berbakat dalam populasi kami, rata-rata, relatif kecil, karena hanya sepertiga dari mereka mencapai total modal yang melebihi yang asli.

Bagaimanapun, fakta bahwa pemain terbaik di antara 100 simulasi berjalan adalah agen dengan bakat T terbaik = 0,6, yang sangat cocok dengan median, dan dengan keberhasilan akhir C terbaik = 40960, yang 650 kali lebih banyak dari C mt , tidak dapat dibantah . dan lebih dari 4.000 kali lebih tinggi daripada keberhasilan C <10 pada 2/3 orang paling berbakat. Ini terjadi, pada akhirnya, hanya karena dia lebih beruntung daripada yang lain. Keberuntungan tanpa syarat, seperti yang dapat dilihat pada Gambar 9, yang menunjukkan pertumbuhan modal / keberhasilannya sepanjang kehidupan kerjanya, bersama dengan serangkaian acara sukses (dan hanya sukses) yang mengesankan, di mana, terlepas dari kurangnya bakat luar biasa, ia dapat mengambil untung selama karier.

Kesimpulannya, pada titik ini ditemukan bahwa, meskipun kesederhanaannya, model TPU tampaknya dapat memperhitungkan banyak fitur yang menjadi ciri, sebagaimana disebutkan dalam pendahuluan, ketidaksetaraan tinggi dalam distribusi kekayaan dan kesuksesan dalam masyarakat kita, yang jelas kontras dengan distribusi bakat Gaussian di antara orang. Juga, model dalam bentuk kuantitatif menunjukkan bahwa talenta hebat tidak cukup untuk karier yang dijamin sukses dan, sebaliknya, orang yang kurang berbakat sering mencapai puncak kesuksesan - ini adalah "fakta kondisional" yang sering diamati dalam kehidupan nyata [35, 36, 38].

Aspek kunci yang secara intuitif menjelaskan bagaimana hal itu bisa terjadi bahwa individu yang berbakat sedang mencapai (begitu sering) kehormatan dan kesuksesan yang jauh lebih besar, dibandingkan dengan yang lebih berbakat, adalah bahwa ada peran keberuntungan yang tersembunyi dan sering diremehkan, seperti yang jelas terlihat. dilihat dari simulasi kami. Tetapi untuk memahami arti sebenarnya dari hasil penelitian kami, penting untuk membedakan antara sudut pandang makro dan mikro.

Faktanya, pada level mikro, mengikuti aturan dinamis dari model TPU, individu yang berbakat adalah apriori lebih mungkin untuk mencapai tingkat kesuksesan yang tinggi daripada yang berbakat, karena ia memiliki kemampuan yang lebih tinggi untuk memanfaatkan peluang. Dengan demikian, dari sudut pandang seorang individu, kita harus menyimpulkan bahwa, tidak dapat (menurut definisi) untuk mempengaruhi penampilan peristiwa sukses, strategi terbaik untuk meningkatkan kemungkinan sukses (di semua tingkat bakat) adalah memperluas aktivitas pribadi, menghasilkan ide, berkomunikasi dengan orang lain, pencarian keragaman dan saling memperkaya. Dengan kata lain, menjadi orang yang berpikiran luas yang siap untuk menghubungi orang lain memberikan kemungkinan tertinggi dari acara yang sukses (yang akan diwujudkan sejauh bakat individu).

Di sisi lain, pada tingkat makro, dari sudut pandang seluruh masyarakat, kemungkinan bertemu orang-orang berbakat di puncak kesuksesan jauh lebih tinggi daripada menemukan orang-orang yang sangat berbakat di sana, karena yang pertama jauh lebih besar dan, berkat keberuntungan, mereka memiliki, secara umum, statistik keuntungan mencapai kesuksesan luar biasa, meskipun kemungkinan priori mereka lebih rendah.

Pada bagian selanjutnya, kami akan mempertimbangkan sudut pandang tingkat makro ini, mengeksplorasi peluang yang ditawarkan oleh model kami untuk mempelajari strategi dan kebijakan yang lebih detail dan lebih rinci untuk meningkatkan tingkat kinerja rata-rata orang paling berbakat dalam populasi, menerapkan cara yang lebih produktif dalam mendistribusikan hadiah dan sumber daya. Bahkan, kami berharap bahwa kebijakan apa pun yang dapat meningkatkan level individu paling berbakat yang merupakan mesin kemajuan dan inovasi di masyarakat kita akan memiliki efek menguntungkan kumulatif.

3. Strategi penyeimbang keberuntungan yang efektif


Hasil yang diberikan pada bagian sebelumnya jelas konsisten dengan bukti empiris yang didokumentasikan dalam pendahuluan, yang mempertanyakan asumsi hampir meritokratis bahwa perbedaan alami dalam bakat, keterampilan, kemampuan, kecerdasan, kerja keras, atau ketekunan adalah satu-satunya alasan untuk sukses. Seperti yang telah kami tunjukkan, keberuntungan juga memiliki dampak dan dapat memainkan peran penting. Inti dari diskusi adalah bahwa, karena sulit diukurnya (dalam banyak kasus, sulit untuk menentukan secara tepat) kualitas pribadi, strategi meritokratis sering digunakan untuk mendistribusikan penghormatan, pembiayaan atau penghargaan, sering berdasarkan hasil pribadi, diukur dalam hal kekayaan pribadi atau kesuksesan. Akibatnya, strategi tersebut mempengaruhi tindakan penguatan lebih lanjut dan memompa kekayaan / keberhasilan individu yang paling sukses karena mekanisme umpan balik positif, yang mirip dengan proses "kaya menjadi kaya" (juga dikenal sebagai "efek Matius" [57, 58, 59]) , dengan hasil yang tidak adil.

Mari kita bayangkan, misalnya, dewan penelitian dan pengembangan yang didanai pemerintah dengan jumlah uang tetap yang dapat digunakan. Apa yang akan jauh lebih efektif untuk meningkatkan keefektifan penelitian rata-rata: memberikan hibah besar hanya untuk beberapa ilmuwan yang unggul atau hibah kecil untuk banyak ilmuwan yang jelas lebih biasa? Sebuah studi baru-baru ini [44], berdasarkan analisis empat indeks signifikansi ilmiah dari publikasi terkait, menemukan bahwa signifikansi hanya memiliki hubungan positif yang lemah dengan pendanaan. Secara khusus, signifikansi dolar lebih rendah bagi pemegang hibah besar, dan signifikansi ilmuwan yang menerima peningkatan pendanaan tidak meningkat ke tingkat yang sesuai. Para penulis penelitian menyimpulkan bahwa signifikansi ilmiah (sebagaimana tercermin dalam publikasi) hanya berbatasan lemah pada pembiayaan, dan menyarankan bahwa strategi pembiayaan yang bertujuan diversifikasi ide daripada "keunggulan" cenderung lebih produktif. Kontribusi kemudian [60] menunjukkan bahwa, baik dalam jumlah dokumen yang dihasilkan dan dalam kepentingan ilmiahnya, dana penelitian terkonsentrasi biasanya mengarah pada penurunan pengembalian marjinal, dan juga bahwa para peneliti yang paling banyak didanai tidak menonjol dalam hal efektivitas dan signifikansi ilmiah. Secara umum, kesimpulan seperti itu seharusnya tidak mengejutkan mengingat penemuan baru-baru ini [18], yang menyatakan bahwa signifikansi, sebagaimana diukur oleh publikasi berpengaruh, didistribusikan secara acak di sejumlah publikasi ilmuwan. Dengan kata lain, keberuntungan itu penting, dan jika itu memengaruhi lebih dari yang ingin kita akui, tidak mengherankan bahwa strategi meritokratis kurang efektif daripada yang diharapkan, terutama jika kita berusaha menghargai jasa posteriori. Dalam studi sebelumnya [48, 49, 50, 51, 52, 53, 54, 55] sudah ada peringatan terhadap "meritokrasi" semacam ini, yang menunjukkan efektivitas strategi alternatif berdasarkan pemilihan acak di bidang manajemen, politik dan keuangan. Menurut sudut pandang ini, model TPU menunjukkan bagaimana tingkat keberhasilan minimum dapat ditingkatkan untuk sebagian besar orang berbakat di dunia di mana keberuntungan penting, dan penemuan tidak disengaja sering mengarah pada pencapaian penting.

3.1. Penemuan tak disengaja, inovasi dan strategi pembiayaan yang efektif


Istilah "penemuan tak disengaja" secara luas digunakan dalam referensi sastra untuk fakta sejarah, menunjukkan bahwa peneliti cukup sering membuat penemuan tak terduga dan berguna secara kebetulan, ketika mereka mencari sesuatu yang lain [61, 62]. Ada daftar panjang kisah-kisah penemuan yang dibuat secara eksklusif oleh kebetulan: dari penisilin oleh Alexander Fleming ke radioaktivitas oleh Marie Curie, dari radiasi latar gelombang mikro kosmik oleh astronom radio Arno Penzias dan Robert Woodrow Wilson ke graphene Andrei Geim dan Konstantin Novosyolov. Berikut adalah contoh yang lebih baru: jaringan saluran yang diisi dengan cairan dalam tubuh manusia, organ yang sebelumnya tidak diketahui yang tampaknya mempromosikan penyebaran sel kanker, ditemukan secara kebetulan, selama endoskopi sederhana [63]. Oleh karena itu, banyak orang berpikir bahwa penelitian yang didorong oleh rasa ingin tahu harus selalu didanai, karena tidak ada yang benar-benar tahu sebelumnya atau memprediksi apa yang mereka tuju [64].

Apakah mungkin untuk mengukur pentingnya penemuan acak? Apa cara paling efektif untuk mensimulasikan penemuan acak? Ini dapat mengambil berbagai bentuk, dan sulit untuk membatasi dan mengukur. Itulah sebabnya, sampai sekarang, studi akademis telah mempertimbangkan penemuan ilmiah yang tidak disengaja, sebagian besar, sebagai konsep filosofis. Tetapi waktu berubah. Dewan Penelitian Eropa baru-baru ini mengalokasikan hibah $ 1,7 juta kepada ahli biokimia Ohid Yakubu untuk menghitung pentingnya penemuan yang tidak disengaja dalam sains [65]. Yakub menemukan bahwa penemuan acak dapat diklasifikasikan ke dalam empat tipe dasar [66] dan bahwa mungkin ada faktor-faktor penting yang mempengaruhi penampilannya. Temuannya tampaknya bertepatan dengan ide-ide dari penelitian sebelumnya [67, 68, 69, 70, 71, 72], yang berpendapat bahwa strategi yang diterima secara umum, jelas meritokratis, yang mengejar keunggulan dan menggantikan keragaman tampaknya ditakdirkan untuk kehilangan dan tidak efektif. Alasannya adalah bahwa mereka secara apriori menolak penelitian yang pada awalnya tampak kurang menjanjikan, tetapi yang, khususnya, berkat penemuan acak, dapat membuat posteriori menjadi sangat inovatif.

Dari sudut pandang ini, kami ingin menerapkan model TPU, yang secara alami menyatakan keberuntungan (dan, akibatnya, penemuan acak) sebagai parameter kuantitatif strategi, untuk mempelajari efektivitas berbagai skenario pembiayaan dalam subbagian ini. Secara khusus, dalam situasi di mana, sebagaimana disebutkan di atas, orang yang cukup berbakat tetapi beruntung sering lebih sukses daripada individu yang lebih berbakat tetapi tidak beruntung, penting untuk mengevaluasi efektivitas strategi pembiayaan untuk kemampuan mempertahankan tingkat keberhasilan minimum, termasuk untuk orang-orang paling berbakat yang diharapkan membawa ide-ide paling inovatif dan progresif.

Dimulai dengan parameter awal yang sama yang digunakan dalam ayat 2.2, yaitu N = 1000, m T = 0,6, σ T = 0,1, I = 80, δ t = 6, C (0) = 10, NE = 500, p L = 50% dan 100 simulasi berjalan, mari bayangkan bahwa total modal pendanaan yang tersedia F T didistribusikan secara berkala di antara individu sesuai dengan berbagai kriteria. Misalnya, keuangan dapat dikeluarkan:
  1. Dibagi bersama (kriteria egaliter) untuk mendorong keragaman penelitian;
  2. Hanya persentase tertentu dari individu yang paling sukses ("terbaik") (kriteria elitis), yang sebelumnya disebut meritokrasi "dekat", untuk distribusi keuangan di antara orang-orang berdasarkan kinerja masa lalu.
  3. Distribusi "premium" di antara proporsi tertentu dari individu yang paling sukses, dan sisanya, dalam bagian kecil yang sama, selama sisanya (kriteria campuran);
  4. Hanya persentase tertentu dari individu yang dipilih secara acak (kriteria acak acak).

Kami realistis berharap bahwa modal total F T akan didistribusikan setiap 5 tahun, untuk jangka waktu 40 tahun, masing-masing simulasi menyapu, sehingga dari waktu ke waktu akan didistribusikan F T unit = 8 modal. Melalui suntikan berkala atas keuangan ini, kami bermaksud untuk mempertahankan tingkat minimum sumber daya dari agen yang paling berbakat. Dengan demikian, indikator yang baik dari efektivitas strategi pembiayaan yang dipilih mungkin persentase P T , rata-rata untuk 100 simulasi berjalan, untuk individu dengan talenta T > m T + σ T , yang total keberhasilan / modalnya melebihi level awal, mis., C end> C (0).

Persentase ini telah dihitung selama simulasi berjalan yang disajikan dalam ayat 2.2. Ini menunjukkan bahwa tanpa adanya dana, kinerja terbaik dicapai oleh agen paling sukses dengan bakat hampir rata-rata, sedangkan modal / kesuksesan orang paling berbakat selalu tetap sangat rendah. Secara khusus, hanya sebagian dari P T0 ≈ 32% dari total jumlah agen dengan talenta T > 0,7 yang dapat dicapai, berdasarkan hasil simulasi, modal / keberhasilan melebihi nilai awal. Oleh karena itu, untuk membandingkan efektivitas berbagai strategi pembiayaan, pertumbuhan persentase rata-rata P T relatif terhadap P T0 harus dihitungorang-orang berbakat yang telah meningkatkan modal awal mereka selama karier mereka. Mari kita mendefinisikan pertumbuhan ini sebagai P * T = P T - P T0 . Nilai ini adalah indikator yang cukup stabil: kami memeriksanya dengan mengulang dari 100 simulasi, penyebaran nilai P * T tetap di bawah 2%. Akhirnya, jika kita menghitung rasio P * T terhadap total modal yang didistribusikan di antara semua agen selama 40 tahun, kita bisa mendapatkan indeks efisiensi E , yang mengukur pertumbuhan jumlah orang-orang berbakat yang cukup sukses per unit modal yang diinvestasikan, yang didefinisikan sebagai E = P * T/ F T .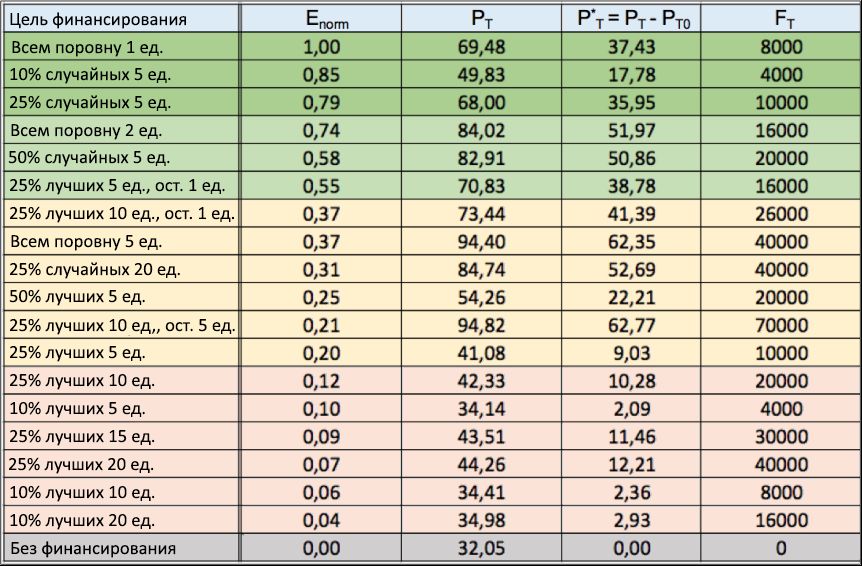


Gambar 10: Tabel strategi pembiayaan. Beberapa strategi untuk mendistribusikan keuangan untuk berbagai keperluan (1 kolom) disajikan, dengan hasil indeks efisiensi normalisasi E norma (2 kolom), dalam urutan menurun. Juga, di kolom ketiga dan keempat, masing-masing, nilai-nilai bagian P T dari orang-orang berbakat yang sukses dan peningkatan bersih dalam jumlah mereka P * T ditunjukkan , sehubungan dengan skenario "tanpa pembiayaan", rata-rata untuk 100 simulasi berjalan. Akhirnya, kolom terakhir menunjukkan total modal F T , diinvestasikan di setiap menguji mereka.

Dalam tabel ditunjukkan pada Gambar 10, kita telah menunjukkan indeks efektivitas (kolom 2) diperoleh selama beberapa strategi alokasi dana, masing-masing dengan tujuannya sendiri keuangan (1 kolom) dan nilai-nilai yang sesuai P T (kolom 3) dan P * T (kolom ke-4). Di kolom yang sama, di kolom terakhir, total modal yang diinvestasikan F T untuk setiap proses diberikan . Indeks efisiensi E dinormalisasi relatif terhadap nilai maksimumnya E max , dan semua catatan (baris) diurutkan berdasarkan kriteria penurunan nilai E norm = E / E max. Untuk skenario dengan kekurangan dana, menurut definisi, E norm = 0. Hasil norma E yang sama ditampilkan sebagai fungsi dari strategi pembiayaan yang diadopsi dalam bentuk histogram pada Gambar 11. Karena stabilitas statistik P T menunjukkan penyimpangan kurang dari 2%, hasil yang diberikan dari E norma stabil.

Ketika mempertimbangkan tabel di atas dan histogram yang sesuai dari Gambar 11, menjadi jelas bahwa jika tujuannya adalah untuk menghargai individu yang paling berbakat (dengan demikian meningkatkan tingkat keberhasilan akhir mereka), jauh lebih baik untuk secara berkala mengalokasikan (bahkan sejumlah kecil) modal untuk semua individu sekaligus, daripada memberikan lebih banyak modal hanya untuk sebagian kecil dari mereka, dipilih sesuai dengan tingkat keberhasilan yang dicapai pada saat distribusi.


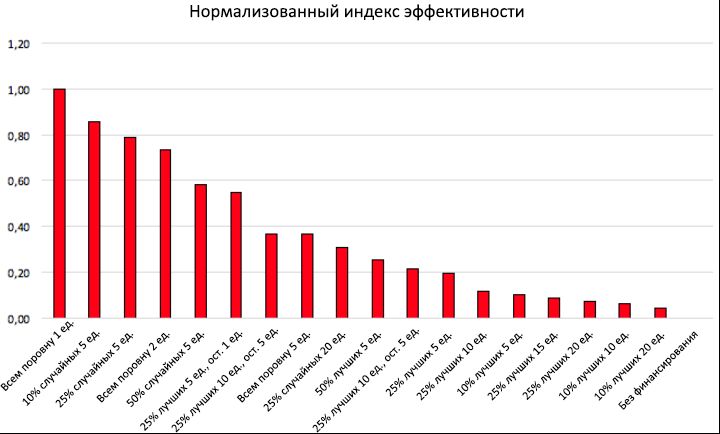Gambar 11: Indeks Kinerja Normalisasi dari beberapa strategi pembiayaan. Nilai indeks efisiensi normalisasi E norma diberikan sebagai fungsi dari berbagai strategi pembiayaan. Angka tersebut menunjukkan bahwa, untuk meningkatkan kesuksesan orang yang lebih berbakat dengan C end> C (0), jauh lebih efisien untuk mendistribusikan sejumlah kecil keuangan di antara banyak individu daripada membiayai dengan cara lain yang lebih selektif.

Di satu sisi, histogram menunjukkan bahwa kriteria "egaliter", yang mengalokasikan 1 unit modal untuk setiap individu setiap 5 tahun, adalah cara paling efisien untuk mendistribusikan keuangan, dengan E norm = 1 (mis., E = E maks ): untuk relatif investasi kecil F T dalam jumlah 8000 unit, ternyata menggandakan persentase orang-orang berbakat yang sukses, dibandingkan dengan skenario "tanpa pembiayaan", memimpinnya dari P T0 = 32,05% ke P T= 69,48%, dengan kenaikan bersih P * T = 37,43. Ketika mempertimbangkan untuk meningkatkan total modal yang diinvestasikan (misalnya, dengan menetapkan kuota pemerataan 2 atau 5 unit), strategi ini juga memastikan peningkatan lebih lanjut dalam persentase akhir dari orang-orang berbakat yang sukses (dari 69,48% menjadi 94,40%), tetapi efisiensi dinormalisasi pada ini berangsur-angsur menurun, dari E norm = 1 ke E norm = 0.74, dan kemudian ke E norm = 0.37, masing-masing.

Di sisi lain, strategi "elit" yang mendistribusikan setiap 5 tahun untuk sejumlah besar keuangan (5, 10, 15, atau 20 unit) hanya di antara yang terbaik 50%, 25%, atau bahkan 10% dari individu yang sudah sukses berada di bagian paling bawah tabel, denganE norma <0,25 di semua skenario, peningkatan bersih di P * T Jumlah total orang-orang berbakat yang sukses, dibandingkan dengan skenario "tanpa pendanaan," sisa-sisa yang sangat rendah (di hampir semua kasus kurang dari 20%), sering jauh lebih diinvestasikan modal, jika dibandingkan dengan strategi egaliter serupa. Hasil-hasil ini memperkuat asumsi bahwa pendekatan semacam itu jelas tidak jauh meritokratis.

Perlu dicatat bahwa penerapan kriteria "campuran", yaitu distribusi bagian keuangan "meritokratis" di antara persentase tertentu dari individu yang paling sukses, misalnya, 25%, dengan distribusi sisa keuangan dalam bagian yang sama kepada orang lain, memberikan hasil yang lebih baik dari indeks kinerja dibandingkan dengan pendekatan "tidak jauh meritokratis". Namun, dalam hal produktivitas, strategi ini tidak mampu mengejar kriteria “egaliter”. Seperti jelas terlihat, misalnya, dari perbandingan garis keempat dan keenam klasemen pembiayaan meskipun total investasi yang sama $ 16.000 unit, nilai P T , sehingga kriteria campuran sisa-sisa lebih rendah dibandingkan dengan pendekatan menyamakan (70,83% vs 84 02%), yang juga dikonfirmasi oleh nilai yang sesuai dari indeks efisiensi Enorma (0,55 vs 0,74).

Jika kita memperhitungkan faktor psikologis (tidak dimodelkan dalam penelitian ini), maka strategi campuran dapat dipertimbangkan kembali dibandingkan dengan yang egaliter. Faktanya, hadiah bonus yang diberikan kepada individu-individu yang paling sukses dapat merangsang kepatuhan yang lebih besar di antara semua agen, sementara sisanya yang terdistribusi secara merata akan memainkan peran ganda: pada tingkat individu, itu akan merangsang keragaman dan memberikan peluang baru bagi orang-orang berbakat yang tidak berhasil untuk menyadari potensi mereka, dan tingkat umum akan mendukung penemuan acak, sehingga berkontribusi pada pengembangan penelitian dan masyarakat secara keseluruhan.

Melihat kembali tabel strategi pembiayaan, perlu memperhatikan efisiensi yang sangat tinggi dari strategi acak, yang menempati dua dari tiga posisi terbaik dalam hasil keseluruhan. Oleh karena itu, misalnya, hadiah berkala 5 unit hanya 10% dari individu yang dipilih secara acak, dengan total investasi hanya 4.000 unit, memberikan peningkatan bersih P * T = 17,78%, yang lebih tinggi daripada hampir semua yang diperoleh dengan menggunakan pemerataan strategi. Selain itu, meningkatkan hingga 25% bagian dari orang-orang yang dibiayai secara acak dan menggandakan total investasi (meningkatkannya menjadi 10.000 unit) memberikan pertumbuhan bersih P * T= 35,95, sebanding dengan yang diperoleh oleh strategi penyamaan terbaik, yang memenangkan tempat pertama di klasemen keseluruhan. Sangat mengejutkan bahwa hasil P * T terakhir ini sekitar empat kali nilainya ( P * T= 9,03%) diperoleh dengan menggunakan pendekatan elitis (lihat baris 12 dari tabel), yang mendistribusikan modal yang persis sama (10.000 unit) di antara jumlah individu yang sama (25% dari total). Yang terakhir ini semakin menegaskan bahwa dalam lingkungan sosial dan ekonomi yang kompleks di mana kesempatan memainkan peran penting, efektivitas strategi lain yang didasarkan pada pemilihan acak dapat dengan mudah melewati strategi standar berdasarkan pendekatan "hampir meritokratis". Fenomena ini, bertentangan dengan akal sehat, telah diamati dalam bidang manajemen, politik dan keuangan [48, 49, 50, 51, 52, 53, 54, 55], dan dengan demikian menemukan konfirmasi lain dalam konteks studi pembiayaan.

Untuk mengkonfirmasi lebih lanjut data yang diperoleh, Gambar. 12 menunjukkan hasil serangkaian simulasi lain. Tidak seperti simulasi sebelumnya, di sini jumlah total modal yang diinvestasikan dalam masing-masing 100 berjalan sekarang ditetapkan pada F T = 80.000, sehingga F T / 8 = 10.000 unit didistribusikan di antara agen setiap 5 tahun , sesuai dengan strategi pembiayaan yang sama yang dibahas sebelumnya . Melihat tabel, kita melihat bahwa hasil dari strategi pemerataan sekali lagi yang paling efektif dalam hal memberi penghargaan kepada orang-orang paling berbakat, dengan bagian P Tmendekati 100%. Ini diikuti oleh strategi acak (dengan 50% individu dipilih secara acak untuk dibiayai), dan kemudian dicampur, di mana setengah dari modal didistribusikan di antara 25% individu yang paling sukses, dan bagian lain, dalam bagian yang sama, di antara orang lain. Sebaliknya, semua strategi elit lagi-lagi ditempatkan di akhir peringkat, dengan demikian semakin menegaskan ketidakefisienan pendekatan "tidak jauh meritokratis" dalam memberi penghargaan kepada talenta sejati.


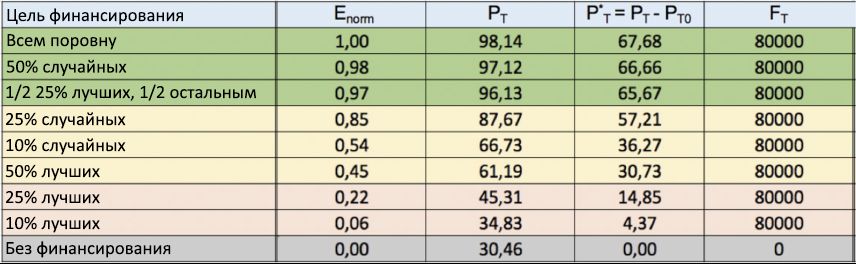Gambar 12: Tabel strategi pembiayaan keuangan tetap. Indeks efisiensi yang dinormalisasi diperoleh E norma untuk beberapa strategi untuk distribusi pembiayaan (kolom 1) sekali lagi ditampilkan dalam urutan menurun, dari atas ke bawah. Berbeda dengan Gambar 10, di sini total modal yang diinvestasikan dalam setiap proses ditetapkan padaF T = 80.000. Strategi pemerataan kembali mengambil tempat pertama.

Hasil simulasi model TPU yang disajikan dalam subbab ini menarik perhatian pada signifikansi faktor-faktor eksternal (seperti, memang, kebijakan pembiayaan yang efektif) dalam meningkatkan peluang keberhasilan bagi sebagian besar individu berbakat yang terlalu sering menemukan diri mereka dihukum oleh kebetulan peristiwa yang tidak berhasil. Pada subbab berikutnya, kami memeriksa sejauh mana peluang baru harus datang dari perubahan lingkungan, seperti tingkat pendidikan atau insentif lain yang berasal dari lingkungan sosial tempat orang tinggal atau dari mana mereka berasal.

3.2. Signifikansi lingkungan


Untuk memulainya, mari kita menilai peran tingkat pendidikan rata-rata di antara populasi. Dalam kerangka model TPU, dapat diperoleh dengan mengubah parameter distribusi bakat normal. Secara umum, jika kita mengasumsikan bahwa bakat dan keterampilan individu, ketika distimulasi, dapat lebih efektif dalam mewujudkan peluang baru, maka peningkatan median m T atau standar deviasi bakat σ T dapat diartikan sebagai konsekuensi dari kebijakan yang diarahkan, masing-masing, baik pada meningkatkan tingkat pendidikan rata-rata, atau untuk memperkuat pelatihan orang-orang yang paling berbakat.

Dalam dua diagram pada Gambar 13, kami menyajikan total modal / kesuksesan yang diakumulasikan oleh berkinerja terbaik dari masing-masing 100 run dalam bentuk fungsi dari talenta mereka. Parameter yang diberikan sesuai dengan yang digunakan pada ayat 2.2 ( N = 1000, I = 80, δ t = 6, C (0) = 10, N E = 500 dan p L = 50%), tetapi dengan momen distribusi bakat yang berbeda . Secara khusus, dalam diagram (a) kami meninggalkan m T = 0,6 yang tidak berubah , tetapi meningkat σ T = 0,2, sedangkan dalam diagram (b) kami melakukan yang sebaliknya, meninggalkan σ T = 0,1 dan menaikkan mT = 0,7. Dalam kedua kasus, Anda dapat melihat pergeseran ke kanan puncak keberhasilan maksimum, tetapi dengan perbedaan dalam detail.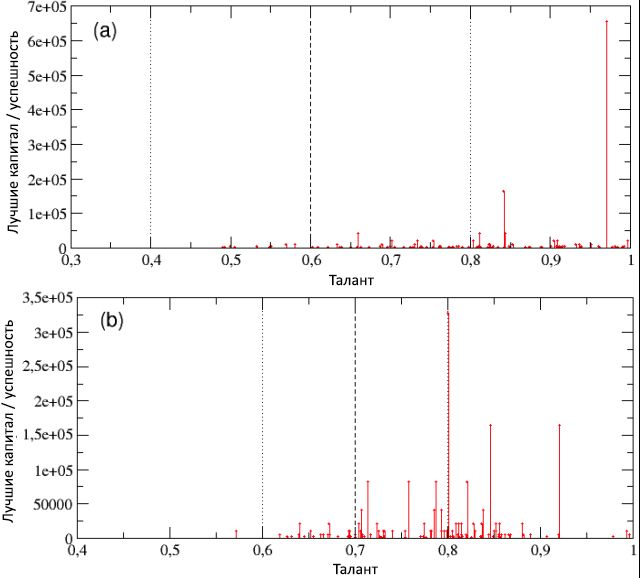


Gambar 13: total modal individu paling sukses di masing-masing 100 berjalan, disajikan sebagai fungsi dari bakat mereka untuk populasi dengan berbagai parameter distribusi bakat: (a) m T = 0,6 dan σ T = 0,2 (yang mencerminkan penguatan akademik melatih orang yang paling berbakat); (B) m T = 0,7 dan σ T = 0,1 (yang menggambarkan peningkatan tingkat rata-rata pendidikan). Juga ditampilkan adalah nilai-nilai yang sesuai m T dan m T ± σ T, dalam bentuk garis putus-putus vertikal dan garis putus-putus, masing-masing.

Bahkan, lead ini fakta bahwa peningkatan σ T , pada nilai konstan m T , seperti yang ditunjukkan dalam diagram (a), meningkatkan kemungkinan orang-orang paling berbakat untuk mencapai keberhasilan sangat tinggi - pemain terbaik sekarang agen yang sangat berbakat, dengan T = 0, 97, yang mencapai tingkat modal luar biasa / keberhasilan C terbaik = 655360. Ini, di satu sisi, dapat dievaluasi secara positif, namun, di sisi lain, ini merupakan kasus yang terisolasi dan ada juga, sebagai penyeimbang, peningkatan kesenjangan antara orang yang beruntung dan yang beruntung. Melihat sekarang pada diagram (b) kita melihat bahwa peningkatan m Ttanpa mengubah σ T memberikan kinerja terbaik dengan C terbaik = 327680 dan bakat T = 0,8, diikuti oleh dua lagi, dengan C = 163840 dan, karenanya, T = 0,85 dan T = 0,92. Ini menunjukkan bahwa dalam kasus ini peluang orang-orang paling berbakat untuk mencapai kesuksesan yang sangat tinggi meningkat, tetapi pada saat yang sama, kesenjangan antara orang yang beruntung dan orang yang beruntung lebih rendah daripada sebelumnya.

Akhirnya, dalam kedua contoh yang dipertimbangkan, nilai rata-rata modal / kesuksesan 100 orang yang paling berbakat dari jumlah orang meningkat sehubungan dengan nilai C mt obtained 63 yang diperoleh pada Subbab 2.2. Secara khusus, kami mendapat Cmt ≈ 319 dalam skema (a) dan C mt ≈ 122 dalam skema (b), tetapi hasil ini sangat spesifik untuk rangkaian simulasi tertentu. Parameter yang lebih dapat diandalkan untuk ekspresi numerik dari efektivitas kebijakan sosial yang dipelajari di sini adalah bahwa itu lagi-lagi indikator P T yang disajikan dalam subbab sebelumnya, yaitu proporsi rata-rata individu dengan talenta T > m T + σ T dan total keberhasilan / modal C akhir > 10, relatif terhadap jumlah total orang dengan talenta T > m T + σ T (perhatikan bahwa di sini, dalam kedua kasus,m T + σ T = 0,8). Jadi, kami mendapat P T = 38% dalam skema (a) dan P T = 37.5% untuk skema (b), dengan sedikit peningkatan bersih relatif terhadap nilai referensi P T0 = 32% (diperoleh untuk distribusi bakat di m T = 0,6 dan σ T = 0,1).

Kesimpulannya, hasil kami menunjukkan bahwa memperkuat pelatihan orang-orang yang paling berbakat atau meningkatkan tingkat rata-rata pendidikan mengarah, seperti yang mungkin diharapkan, ke beberapa efek positif dalam sistem sosial, karena kedua kebijakan ini mengarah pada peningkatan kemungkinan individu berbakat untuk mewujudkan peluang, memberi mereka keberuntungan. Di sisi lain, peningkatan dalam bagian rata-rata orang yang sangat berbakat yang berhasil mencapai tingkat keberhasilan yang baik tampaknya tidak terlalu signifikan untuk kedua skenario yang dianalisis. Dengan demikian, hasil dari kebijakan pendidikan yang relevan tampaknya sebagian besar terbatas pada kejadian terisolasi yang luar biasa.

Tentu saja, setelah tingkat pendidikan ini ditetapkan, menjadi jelas bahwa banyaknya peluang yang ditawarkan oleh lingkungan sosial itu, yaitu negara tempat seseorang dilahirkan secara tidak sengaja atau memutuskan untuk tinggal adalah komponen kunci lain yang dapat mempengaruhi kinerja sistem global.

Pada Gambar 14, kami mempresentasikan hasil yang mirip dengan yang terlihat pada gambar sebelumnya, tetapi untuk seri simulasi lainnya, masing-masing 100 berjalan, dengan parameter yang sama seperti pada ayat 2.2 ( N = 1000, m T = 0, 6, σ T = 0,1, I = 80, C (0) = 10, N E = 500) tetapi dengan persentase berbeda p LPeristiwa sukses (ingat bahwa dalam ayat 2.2 persentase p L = 50% diambil ). Dalam skema (a), kami mengambil p L = 80% untuk mensimulasikan lingkungan yang sangat merangsang penuh peluang, khas negara industri kaya seperti Amerika Serikat [26]. Di sisi lain, dalam skema (b), nilai p L = 20% mereproduksi skenario lingkungan yang jauh kurang menggembirakan, dengan sejumlah kecil kemungkinan, seperti, misalnya, di negara-negara Dunia Ketiga.


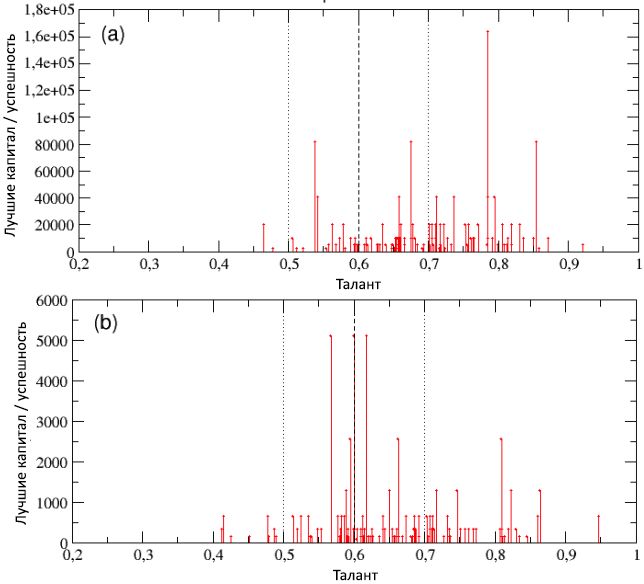Gambar 14: total modal individu paling sukses di masing-masing 100 berjalan ditunjukkan sebagai fungsi dari bakat mereka untuk populasi yang tinggal di lingkungan dengan persentase yang berbeda p L peristiwa sukses: (a) pL = 80%; (B) p L = 20%. Juga, tanda garis putus-putus dan garis putus-putus, masing-masing, nilai-nilai m T = 0,6 dan m T ± σ T , dengan σ T = 0,1.

Seperti yang terlihat di kedua skema, final keberhasilan / modal individu yang paling beruntung ditampilkan sebagai fungsi bakat mereka, sangat tergantung pada p L .

Pada p L = 80%, seperti dalam skema (a), beberapa agen dengan bakat menengah-tinggi mampu mencapaitingkat kesuksesan yanglebihtinggidibandingkan dengan skenario p L = 50%, dengan puncak Cterbaik = 163840. Di sisi lain, nilai rata-rata modal / keberhasilan individu yang paling berbakat, C mt ≈ 149, cukup tinggi dan, yang lebih penting, hal yang sama berlaku untuk indikator P T = 62,18% (yaitu sekitar dua kali lipat lebih banyak nilai referensi P T0 = 32%), ini berarti bahwa, seperti yang diharapkan, orang yang paling berbakat mendapat manfaat dari persentase yang lebih besar dari acara yang sukses.

Hasil yang sama sekali berbeda diperoleh dengan p L = 20%. Tentu saja, seperti yang dapat dilihat dari skema (b), tingkat keberhasilan keseluruhan sekarang sangat rendah dibandingkan dengan apa yang ditemukan dalam simulasi dari ayat 2.2, dengan nilai puncak C terbaikberjumlah hanya 5120 unit - ini adalah jejak penurunan kesenjangan sosial, yang merupakan konsekuensi yang diharapkan dari menyamakan peluang dalam mencapai kesuksesan. Menurut hasil ini, indeks P T juga mencapai nilai minimum, dengan persentase rata-rata individu berbakat yang mampu meningkatkan tingkat keberhasilan awal sama menjadi 8,75% saja.

Sebagai hasilnya, pada bagian ini ditunjukkan bahwa lingkungan yang menggembirakan dan banyaknya peluang yang terkait dengan strategi yang tepat untuk mengalokasikan keuangan dan sumber daya merupakan faktor penting dalam mewujudkan potensi orang-orang paling berbakat, memberi mereka lebih banyak peluang untuk mencapai kesuksesan dibandingkan dengan yang berbakat, tetapi lebih beruntung Dari sudut pandang tingkat makro, setiap kebijakan yang dapat memengaruhi indikator-indikator ini dan mendukung individu-individu berbakat akan menghasilkan kemajuan dan inovasi kolektif.

4. Komentar akhir


Dalam makalah ini, dimulai dengan sejumlah asumsi yang sangat sederhana dan rasional, kami mempresentasikan model agen yang mampu mengukur secara kuantitatif peran bakat dan keberuntungan dalam keberhasilan karier orang. Simulasi menunjukkan bahwa meskipun bakat memiliki distribusi Gaussian antara agen, distribusi akhir kesuksesan / modal, setelah 40 tahun kehidupan kerja, mengikuti fungsi kekuasaan sesuai dengan prinsip hukum Pareto "80/20", yang sesuai dengan sifat distribusi kekayaan yang diamati di dunia nyata. Hasil penting dari simulasi adalah bahwa agen yang paling sukses hampir selalu bukan yang paling berbakat, tetapi mereka yang dekat dengan nilai rata-rata distribusi bakat Gaussian - fakta yang dikenal luas sering ditemukan dalam literatur.Model ini menunjukkan pentingnya peristiwa sukses yang sering dianggap remeh dalam menentukan tingkat akhir kesuksesan individu. Karena penghargaan dan sumber daya biasanya didistribusikan kepada mereka yang telah mencapai tingkat kesuksesan yang tinggi, yang secara keliru digunakan sebagai ukuran kompetensi / bakat, ini mengarah pada insentif negatif, yang menyebabkan kurangnya kesempatan untuk talenta tertinggi. Hasil kami menekankan risiko dari paradigma yang kami sebut "nyaris meritokrasi," yang tidak dapat menghormati dan menghargai orang yang paling kompeten, karena itu meremehkan peran peluang di antara faktor penentu keberhasilan utama. Dalam hal ini, beberapa skenario berbeda dipelajari untuk mengidentifikasi strategi yang paling efektif yang dapat menyeimbangkan peran keberuntungan yang tidak terduga dan memberikan lebih banyak peluang dan sumber daya ke yang paling berbakat - maksudnya,yang seharusnya menjadi tujuan utama dari pendekatan yang benar-benar meritokratis. Itu juga menunjukkan bahwa strategi ini paling bermanfaat bagi masyarakat secara keseluruhan, karena mengarah pada pertumbuhan berbagai ide dan perspektif dalam penelitian, dengan demikian juga merangsang inovasi.

Ucapan Terima Kasih


Kami ingin berterima kasih kepada Robert Frank, Pavel Sobkowitz, dan Konstantino Tsallis untuk diskusi dan komentar yang bermanfaat.

Daftar pustaka


  1. Bak, P., Tang, C. dan Wiesenfeld, K., kekritisan yang diatur sendiri. Phys Rev. A , 38: 364 {374 (1988).
  2. Barabasi, A.-L., Albert, R., Kemunculan Penskalaan dalam Jaringan Acak, Sains , Vol. 286, Edisi 5439, hlm. 509 {512 (1999).
  3. Newman, MEJ, hukum Power, distribusi Pareto dan hukum Zipf, Fisika Kontemporer , 46 (5): 323 {351 (2005).
  4. Tsallis, C., Pengantar Mekanika Statistik Nonextensive. Mendekati Dunia yang Kompleks , Springer (2009).
  5. Pareto, V., Cours d'Economique Politique , vol. 2 (1897).
  6. Steindl, J., Random Processes and the Growth of Firms — A Study of the Pareto Law, Charles Griffin and Company , London (1965).
  7. Atkinson, AB, Harrison, AJ, Distribution of Total Wealth in Britain, Cambridge University Press , Cambridge (1978).
  8. Persky, J., Retrospectives: Pareto's law, Journal of Economic Perspectives 6, 181{192 (1992).
  9. Klass, OS, Biham, O., Levy, M., Malcai, O., Solomon, S., The Forbes 400 and the Pareto wealth distribution, Economics Letters 90, 290{295 (2006).
  10. Hardoon, D., An economy for the 99% , Oxfam GB, Oxfam House, John Smith Drive, Cowley, Oxford, OX4 2JY, UK (January 2017).
  11. Bouchaud, J.-P., M´ezard, M., Wealth condensation in a simple model of economy, Physica A 282, 536{54 (2000).
  12. Dragulescu, A. and Yakovenko, VM, Statistical mechanics of money, Eur. Phys. J. B 17, 723{729 (2000).
  13. Chakraborti, A. and Chakrabarti, BK, Statistical mechanics of money: how saving propensity affects its distribution, Eur. Phys. J. B 17, 167{170 (2000).
  14. Patriarca, M., Chakraborti, A., Germano, G., Influence of saving propensity on the power law tail of wealth distribution, Physica A 369(2), 723{736 (2006).
  15. Scalas, E., Random exchange models and the distribution of wealth. European Physical Journal — Special Topics , 225. pp. 3293-3298. ISSN 1951{6355 (2016).
  16. During, B., Georgiou, N. and Scalas, E., A stylised model for wealth distribution. In Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95{117. ISBN 9789811057045 (2017).
  17. During, Bertram, Georgiou, Nicos and Scalas, Enrico (2017) A stylised model for wealth distribution. In: Akura, Yuji and Kirman, Alan (eds.) Economic Foundations of Social Complexity Science . Springer Singapore, Singapore, pp. 95-117. ISBN 9789811057045
  18. Sinatra, R., Wang, D., Deville, P., Song, C. and Barab´asi, A.-L., Quantifying the evolution of individual scientific impact, Science 354, 6312 (2016).
  19. Einav, L. and Yariv, L., What's in a Surname? The Effects of Surname Initials on Academic Success, Journal of Economic Perspective , Vol. 20, n. 1, p.175{188 (2006).
  20. Ruocco, G., Daraio, C., Folli, V. and Leonetti, M., Bibliometric indicators: the origin of their log-normal distribution and why they are not a reliable proxy for an individual scholar's talent, Palgrave Communications 3:17064 doi: 10.1057/palcomms.2017.64 (2017).
  21. Jurajda, S., Munich, D., Admission to Selective Schools, Alphabetically, Economics of Education Review , Vol. 29, n. 6, p.1100{1109 (2010).
  22. Van Tilburg, WAP, Igou, ER, The impact of middle names: Middle name initials enhance evaluations of intellectual performance, European Journal of Social Psychology , Vol. 44, Issue 4, p.400{411 (2014).
  23. Laham, SM, Koval, P., Alter, AL, The name-pronunciation effect: Why people like Mr. Smith more than Mr. Colquhoun, Journal of Experimental Social Psychology 48, p.752{756 (2012).
  24. Silberzahn, R., Uhlmann, EL, It Pays to be Herr Kaiser: Germans with Noble-Sounding Last Names More Often Work as Managers, Psychological Science 24(12): 2437{44 (2013).
  25. Coffey, B. and McLaughlin, P., From Lawyer to Judge: Advancement, Sex, and NameCalling. SSRN Electronic Journal , DOI10.2139/ssrn.1348280 (2009).
  26. Milanovic, B., Global Inequality of Opportunity: How Much of Our Income Is Determined by Where We Live?, Review of Economics and Statistics , 97.2 (2015): 452{60.
  27. Du, Q., Gao, H., Levi, MD, The relative-age effect and career success: Evidence from corporate CEOs, Economics Letters 117(3):660{662 (2012).
  28. Deaner, RO, Lowen, A., Cobley, S., Born at the Wrong Time: Selection Bias in the NHL Draft. PLoS ONE 8(2): e57753 (2013).
  29. Brooks, D., The Social Animal. The Hidden Sources of Love, Character, and Achievement, Random House , 424 pp. (2011).
  30. Iacopini, I., Milojevic, S. and Latora, V., Network Dynamics of Innovation Processes, Physical Review Letters 120, 048301 (2018).
  31. Tomasetti, C., Li, L., Vogelstein, B., Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention, Science 355, 1330{1334 (2017).
  32. Newgreen, DF et al., Differential Clonal Expansion in an Invading Cell Population: Clonal Advantage or Dumb Luck?, Cells Tissues Organs 203:105{113 (2017).
  33. Snyder, RE and Ellner, SP, We Happy Few: Using Structured Population Models to Identify the Decisive Events in the Lives of Exceptional Individuals, The American Naturalist 188, no. 2 (2016): E28{E45.
  34. Snyder, RE and Ellner, SP, Pluck or Luck: Does Trait Variation or Chance Drive Variation in Lifetime Reproductive Success?, The American Naturalist 191, no. 4 (2018): E90{E107.
  35. .., . , , (2018).
  36. .., . , (2018).
  37. Mauboussin, MJ, The Success Equation: Untangling Skill and Luck in Business, Sports, and Investing, Harvard Business Review Press (2012).
  38. .., . , (2019).
  39. Watts, DJ, Everything Is Obvious: Once You Know the Answer , Crown Business (2011).
  40. Salganik, MJ, Dodds PS, Watts DJ, Experimental Study of Inequality and Unpredictability in an Artificial Cultural Market, Science Vol.311 (2006)
  41. Travis, M., Hofman, JM, Sharma, A., Anderson,. A., Watts, DJ, Exploring limits to prediction in complex social systems , Proceedings of the 25th ACM International World Wide Web Conference (2016) arXiv:1602.01013 [cs.SI]
  42. Stewart, J., The Distribution of Talent, Marilyn Zurmuehlin Working Papers in Art Education 2 : 21-22 (1983).
  43. Sinha, S. and Pan, RK, How a «Hit» is Born: The Emergence of Popularity from the Dynamics of Collective Choice, In Econophysics and Sociophysics: Trends and Perspectives (eds BK Chakrabarti, A. Chakraborti and A. Chatterjee), Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany. doi: 10.1002/9783527610006.ch15 (2006).
  44. Fortin, J.-M., Curr, DJ, Big Science vs. Little Science: How Scientific Impact Scales with Funding, PLoS ONE 8(6): e65263 (2013).
  45. Jacob, BA, Lefgren, L., The impact of research grant funding on scientific productivity, Journal of Public Economics 95 (2011) 1168{1177.
  46. O'Boyle, JR. E. and Aguinis, H., The Best and the Rest: revisiting the norm of normality of individual performance, Personnel Psychology , 65: 79-119. doi:10.1111/j.1744-6570.2011.01239.x (2012).
  47. Denrell, J. and Liu, C., Top performers are not the most impressive when extreme performance indicates unreliability, Proceedings of the National Academy of Sciences , 109(24):9331{9336 (2012).
  48. Pluchino, A., Rapisarda, A., and Garofalo, C., The Peter principle revisited: A computational study, Physica A 389(3):467{472 (2010).
  49. Pluchino, A., Garofalo, C., Rapisarda, A., Spagano, S. and Caserta, M., Accidental politicians: How randomly selected legislators can improve parliament efficiency, Physica A 390(21):3944{3954 (2011).
  50. Pluchino, A., Rapisarda, A. and Garofalo, C., Efficient promotion strategies in hierarchical organizations, Physica A 390(20):3496{3511 (2011).
  51. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Reducing financial avalanches by random investments, Phys. Rev. E 88(6):062814 (2013).
  52. Biondo, AE, Pluchino, A., Rapisarda, A., Helbing, D., Are random trading strategies more successful than technical ones, PLoS One 8(7):e68344 (2013)
  53. Biondo, AE, Pluchino, A., Rapisarda, A., The beneficial role of random strategies in social and financial systems, J. Stat. Phys. 151(3-4):607{622 (2013).
  54. Biondo, AE, Pluchino, A., Rapisarda, A., Micro and macro benefits of random investments in financial markets, Cont. Phys. 55(4):318{334 (2014).
  55. Biondo, AE, Pluchino, A., Rapisarda, A., Modeling financial markets by self-organized criticality, Phys. Rev. E 92(4):042814 (2015).
  56. Wilensky, U., NetLogo. ccl.northwestern.edu/netlogo . Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL (1999).
  57. Merton, RK, The Matthew effect in science, Science 159, 56-63 (1968).
  58. . ., , II: , https://www.hse.ru/data/033/314/1234/3_6_1Merto.pdf .
  59. Bol, T., de Vaan, M. and van de Rijt, A., The Matthew effect in science funding, Proceedings of the National Academy of Sciences , DOI: 10.1073/pnas.1719557115 (2018).
  60. Mongeon, P., Brodeur, C., Beaudry, C. et al., Concentration of research funding leads to decreasing marginal returns, Research Evaluation 25, 396{404 (2016).
  61. Merton, RK, Barber, E., The Travels and Adventures of Serendipity , Princeton University Press, Princeton (2004).
  62. Murayama, K. et al., Management of science, serendipity, and research performance, Research Policy 44 (4), 862{873 (2015).
  63. Benias, PC et al., Structure and Distribution of an Unrecognized Interstitium in Human Tissues, Scientific Reports , vol. 8, 4947 (2018).
  64. Flexner, A, The Usefulness of Useless Knowledge , Princeton University Press, Princeton (2017).
  65. Lucky science. Scientists often herald the role of serendipity in research. A project in Britain aims to test the popular idea with evidence. , Nature Editorial, Vol.554, 1 February 2018.
  66. Yaqub, O., Serendipity: Towards a taxonomy and a theory, Research Policy 47, 169{179 (2018).
  67. Page, SE, The Diversity Bonus. How Great Teams Pay Off in the Knowledge Economy , Princeton University Press (2017).
  68. Cimini, G., Gabrielli, A., Sylos Labini, F., The Scientific Competitiveness of Nations, PLoS ONE 9(12): e113470. doi.org/10.1371/journal.pone.0113470 (2014).
  69. Curry, S., Let's move beyond the rhetoric: it's time to change how we judge research, Nature 554, 147 (2018).
  70. Nicholson, JM and Ioannidis, JPA, Research grants: Conform and be funded, Nature 492, 34{36 (2012).
  71. Bollen, J., Crandall, D., Junk, D. et al., An efficient system to fund science: from proposal review to peer-to-peer distributions, Scientometrics 110, 521{528 (2017).
  72. Garner, HR, McIver, LJ and Waitzkin, MB, Research funding: Same work, twice the money?, Nature 493,599{601 (2013).


: Talent vs Luck: the role of randomness in success and failure

Source: https://habr.com/ru/post/id455064/

More articles:


All Articles