Pohon pencarian biner seimbang: implementasi pada Julia

Ilustrasi dari karya G.M. Adelson-Welsky dan E.M. Landis 1962

Pohon pencarian adalah struktur data untuk penyimpanan teratur dan pencarian sederhana untuk item. Pohon pencarian biner banyak digunakan, di mana setiap node hanya memiliki dua anak. Dalam artikel ini, kami mempertimbangkan dua metode untuk mengatur pohon pencarian biner: algoritma Adelson-Welsky dan Landis (pohon AVL) dan pohon AVL yang melemah (pohon WAVL).

Mari kita mulai dengan definisi. Pohon biner terdiri dari node , setiap node menyimpan catatan dalam bentuk pasangan kunci-nilai (atau, dalam kasus sederhana, hanya nilai) dan tidak memiliki lebih dari dua anak . Node turunan dibedakan oleh kanan dan kiri , dan kondisi untuk pemesanan kunci terpenuhi: kunci anak kiri tidak lebih, dan yang kanan tidak kurang dari kunci node induk. Selain itu, informasi layanan dapat disimpan (dan biasanya disimpan) dalam node - misalnya, tautan ke simpul induk atau data lainnya. Kasus khusus adalah simpul akar dari mana pohon masuk, dan simpul kosong yang tidak menyimpan informasi apa pun. Node di mana kedua keturunannya kosong disebut daun pohon. Node dengan semua keturunan membentuk subtree . Jadi, setiap simpul adalah akar dari pohon subtree atau daun.

Definisi ini memungkinkan Anda untuk membangun struktur sederhana untuk menyimpan node dan pohon itu sendiri. Kami berasumsi bahwa simpul kosong memiliki nilai khusus nothing . Kemudian dalam node itu sudah cukup untuk menyimpan referensi ke keturunan kanan dan kiri dan ke induknya. Struktur untuk menyimpan pohon hanya berisi tautan ke simpul akar.

 # K -   # V -    mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} end mutable struct BST{K, V} root::BSTNode{K,V} end 

Dalam kasus ini, muncul pertanyaan tentang bagaimana merepresentasikan pohon kosong. Untuk melakukan ini, kami menggunakan pendekatan dari buku "Algoritma: Konstruksi dan Analisis" dan memasukkan sebagai titik masuk ke pohon bukan root, tetapi simpul dummy, yang akan menjadi induknya sendiri. Untuk membuat simpul seperti itu, tambahkan konstruktor ke deskripsi struktur BSTNode:

 mutable struct BSTNode{K, V} key::K value::V left::Union{Nothing, BSTNode{K,V}} right::Union{Nothing, BSTNode{K,V}} parent::BSTNode{K,V} #   function BSTNode{K,V}() where {K,V} node = new{K,V}() node.parent = node node.left = node.right = nothing return node end #    - function BSTNode{K,V}(key, value) where {K, V} node = new{K,V}() node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end BSTNode() = BSTNode{Any, Any}() #     ! struct BST{K, V} entry::BSTNode{K,V} BST{K,V}() where {K,V} = new{K,V}(BSTNode{K,V}()) end BST() = BST{Any, Any}() Base.isempty(bst::BST) = bst.entry.left == nothing 

Dalam hal ini, struktur BST dapat dibuat tidak berubah, karena tautan ke titik masuk tidak perlu lagi diubah. Lebih lanjut, kita mengasumsikan bahwa simpul akar pohon adalah keturunan kanan dan kiri dari simpul input.

Operasi utama yang membutuhkan pohon pencarian adalah, tentu saja, pencarian elemen. Karena kunci anak kiri tidak lebih, dan yang kanan tidak kurang dari kunci induk, prosedur pencarian elemen ditulis dengan sangat sederhana: mulai dari akar pohon, bandingkan kunci input dengan kunci simpul saat ini; jika kunci cocok, kami mengembalikan nilainya, jika tidak, pergi ke subtree kiri atau kanan, tergantung pada urutan tombol. Jika pada saat yang sama mereka mencapai simpul kosong - tidak ada kunci di pohon, berikan pengecualian.

 #   Base.getindex()    #      tree[key] function Base.getindex(bst::BST{K,V}, key) where {K,V} key = convert(K, key) node = bst.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

Mencari elemen dengan kunci, jelas, membutuhkan waktu O ( h ), di mana h adalah ketinggian pohon, mis. jarak maksimum dari akar ke daun. Sangat mudah untuk menghitung bahwa pohon biner dengan tinggi h dapat mengandung paling banyak 2 ^{jam + 1} -1 node jika padat penduduk , mis. semua node, kecuali, mungkin, lapisan yang paling ekstrim, memiliki kedua keturunan. Selain itu, jelas bahwa urutan tombol apa pun yang diberikan di muka dapat menyebabkan pohon yang padat. Ini memberikan asimtotik yang sangat optimis untuk menemukan elemen dalam pohon ketika dibangun secara optimal dalam waktu O (log ₂ N ), di mana N adalah jumlah elemen.

Tentu saja, algoritma untuk menambahkan elemen ke pohon pencarian perlu dibangun sedemikian rupa sehingga kondisi pada urutan tombol terpenuhi. Mari kita menulis implementasi naif dari memasukkan elemen dengan kunci:

 #   Base.setindex!()    #       tree[key] = value function Base.setindex!(bst::BST{K,V}, val::SV, key::SK) where {K, V} key, value = convert(K, key), convert(V, val) parent = bst.entry.left #   -     if parent == nothing newnode.parent = bst.entry bst.entry.left = bst.entry.right = newnode return val end key_found = false while !key_found if key < parent.key if parent.left == nothing parent.left = BSTNode{K,V}(key, value) parent.left.parent = parent key_found = true else parent = parent.left end elseif key > parent.key if parent.right == nothing parent.right = BSTNode{K,V}(key, value) newnode.parent = parent key_found = true else parent = parent.right end else key_found = true parent.value = value end end return val end 

Sayangnya, konstruksi naif pohon akan memberikan struktur yang diinginkan hanya pada data input acak, tetapi pada kenyataannya mereka seringkali cukup terstruktur. Dalam kasus terburuk, jika kunci yang masuk diatur secara ketat (setidaknya dalam urutan naik, setidaknya dalam urutan menurun), konstruksi pohon naif akan mengirim elemen baru sepanjang waktu dalam satu arah, mengumpulkan, pada kenyataannya, daftar linier. Sangat mudah untuk menebak bahwa penyisipan elemen, bahwa pencarian akan terjadi dengan struktur seperti itu selama O ( N ), yang meniadakan semua upaya untuk membangun struktur data yang kompleks.

Kesimpulan: pohon pencarian harus seimbang selama konstruksi, mis. menyelaraskan ketinggian subtree kanan dan kiri di setiap node. Ada beberapa pendekatan untuk menyeimbangkan. Yang paling sederhana adalah menentukan sejumlah operasi penyisipan atau penghapusan tertentu, setelah itu pohon akan diseimbangkan kembali. Dalam kasus ini, pohon akan berada dalam kondisi yang agak "berjalan" sebelum menyeimbangkan, karena itu penyeimbangan akan memakan waktu sekitar O ( N ) dalam kasus terburuk, tetapi operasi selanjutnya hingga batas penyisipan / penghapusan tertentu akan dilakukan dalam waktu logaritmik. Pilihan lain adalah membangun algoritma penyisipan dan penghapusan segera sehingga pohon selalu tetap seimbang, yang memberikan kompleksitas waktu yang dijamin O (log ₂ N ) untuk operasi apa pun.

Karena kenyataan bahwa ada algoritma di mana pohon diizinkan untuk "menjadi liar", tetapi setelah itu, operasi dapat dilakukan untuk waktu yang agak lama dalam waktu logaritmik, sebelum pohon harus dibawa kembali ke keadaan seimbang untuk waktu yang lama, waktu penyisipan / penghapusan yang dijamin dan diamortisasi dibedakan. Untuk beberapa implementasi operasi dengan pohon pencarian biner, kompleksitas memasukkan dan menghapus O (log ₂ N ) dijamin, untuk beberapa itu diamortisasi, dengan deteriorasi ke O ( N ).

Adelson-Welsky dan Landis Algorithm (AVL)

Implementasi pertama pohon pencarian biner yang menyeimbangkan diri diusulkan pada tahun 1962 oleh Adelson-Welsky dan Landis. Dalam literatur modern tentang huruf awal nama keluarga, struktur ini disebut AVL-tree . Struktur dijelaskan oleh properti berikut:

1. Pemesanan: untuk setiap simpul, kunci di bagian atas subtree kiri lebih besar daripada di bagian atas subtree kanan daripada kunci node itu sendiri (jika turunannya bukan node kosong).
2. Peningkatan tinggi: ketinggian simpul orangtua adalah satu lebih dari ketinggian maksimum turunannya. Ketinggian node kosong dapat dianggap sama dengan nol.
3. Keseimbangan AVL: untuk setiap simpul, ketinggian sub pohon kanan dan kiri berbeda tidak lebih dari 1.

Dari sifat-sifat ini dapat disimpulkan bahwa ketinggian seluruh pohon adalah O (log ₂ N ), di mana N adalah jumlah catatan yang disimpan di pohon, yang berarti bahwa catatan tersebut dicari dalam waktu logaritmik. Agar kondisi keseimbangan ABL tetap setelah setiap penyisipan, setiap penyisipan disertai dengan operasi penyeimbangan . Untuk implementasi operasi ini yang efektif, setiap node perlu menyimpan informasi layanan. Untuk kesederhanaan, pertahankan ketinggian simpul di sana.

 mutable struct AVLNode{K,V} # ,       255 # (  10^38 ) height::UInt8 key::K value::V left::Union{Nothing, AVLNode{K,V}} right::Union{Nothing, AVLNode{K,V}} parent::AVLNode{K,V} #   function AVLNode{K,V}() where {K,V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing return node end #    - function AVLNode{K,V}(key::SK, value::SV) where {K, V, SK<:K, SV<:V} node = new{K,V}() node.height = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end avlheight(node::Union{Nothing,AVLNode}) = node == nothing ? 0 : Int(node.height) 

Sisipkan catatan

Penyisipan dasar dilakukan sesuai dengan algoritma standar - turun pohon, cari di mana Anda dapat memasukkan simpul baru dan masukkan. Kami akan menulis pembungkus untuk mendapatkan dan mengganti simpul anak menggunakan indeks -1 dan 1 alih-alih kiri dan kanan:

 function child(root::AVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function insert_child!(root::AVLNode{K,V}, newnode::Union{Nothing,AVLNode{K,V}}, side::Signed) where {K,V} newnode == nothing || (newnode.parent = root) if side == -1 root.left = newnode elseif side == 1 root.right = newnode else throw(ArgumentError("Expecting side=-1 for inserting node to the left or side=1 for inserting to the right")) end end 

Selanjutnya, kita naik pohon dan mencari pelanggaran kondisi 2 dan 3. Selanjutnya, kita mempertimbangkan opsi yang mungkin muncul (dalam gambar, hijau menunjukkan simpul yang mengubah ketinggian, simpul yang sedang diproses adalah induknya).

Kasing 0
Setelah penyisipan, ketinggian simpul menjadi sama dengan saudara perempuan, dan 1 kurang dari tinggi (tua) dari simpul induk.

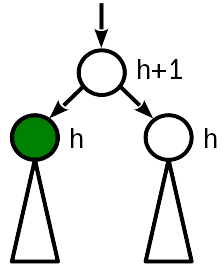
Kasus terbaik, tidak perlu menyentuh apa pun lebih lanjut. Di atas juga, Anda tidak bisa lagi menonton, karena tidak ada yang akan berubah di sana.

Kasus 1
Sebelum dimasukkan, ketinggian simpul sama dengan tinggi simpul adik. Penyisipan mengangkat akar subtree, dan ketinggian node dibandingkan dengan ketinggian induk.

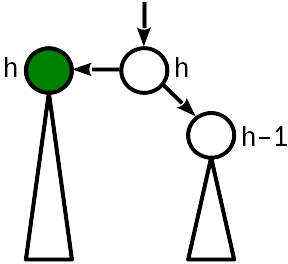
Dalam hal ini, cukup untuk "menaikkan" simpul induk, menambah ketinggiannya dengan 1. Pada saat yang sama, Anda harus terus berpindah ke akar pohon, karena mengubah ketinggian simpul induk dapat menyebabkan pelanggaran kondisi 2 satu tingkat lebih tinggi.

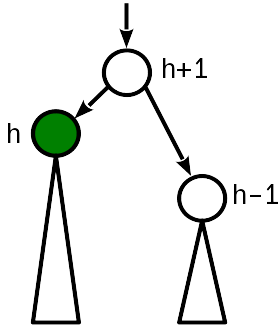
 fucntion promote!(nd::AVLNode, by::Integer=1) nd.height += by end fucntion demote!(nd::AVLNode, by::Integer=1) nd.height -= by end 

Kasus 2

Setelah penyisipan, perbedaan ketinggian dengan subtree sister menjadi 2, dan subtree kiri "didorong" ke atas:

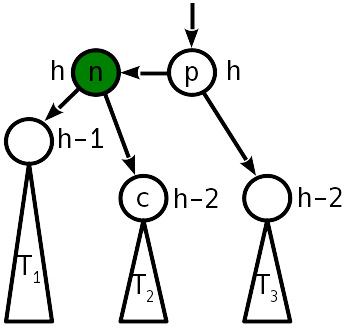
Masalahnya ditangani dengan operasi yang disebut "rotasi sederhana" yang mengubah pohon sebagai berikut:

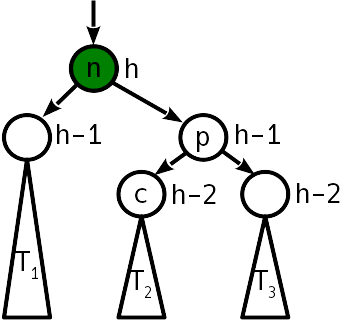
Giliran sederhana membutuhkan 6 perubahan pointer.

Perhatikan bahwa dalam proyeksi ke sumbu horizontal, urutan simpul n , p dan pohon T ₁ - T ₃ sebelum dan sesudah rotasi tetap sama. Ini adalah pemenuhan kondisi pemesanan. Seperti yang Anda lihat, setelah menyalakan pohon, keseimbangan tidak lagi diperlukan.

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end 

Kasus 3
Setelah penyisipan, perbedaan ketinggian dengan subtree sister menjadi 2, dan subtree kanan "didorong" ke atas:

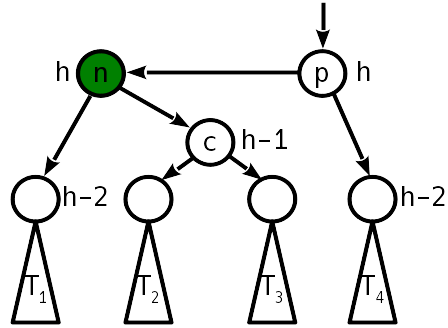
Dalam hal ini, satu belokan sederhana tidak akan lagi membantu, tetapi Anda dapat membuat belokan kiri sederhana di sekitar keturunan kanan, yang akan mengarah ke kasus 2, yang sudah ditangani dengan belokan kanan sederhana.

Untuk mengurangi jumlah "lebih banyak" dari node, dua putaran dapat digabungkan menjadi satu operasi, yang disebut putaran besar, atau ganda. Kemudian, alih-alih 12 perubahan pointer, hanya diperlukan 10. Sebagai hasil dari rotasi ganda, pohon mengambil bentuk berikut:

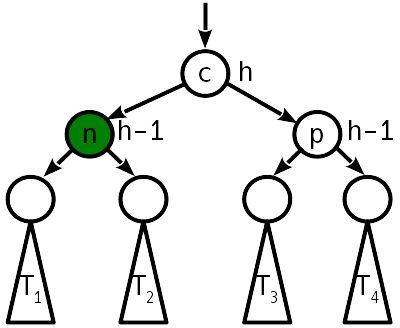
Seperti yang Anda lihat, setelah belokan ganda, keseimbangan lebih lanjut pada pohon juga tidak diperlukan.

 # pivot       funtion double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end 

Jadi, ketika Anda memasukkan catatan ke pohon AVL, Anda perlu O (log ₂ N ) perubahan informasi tentang ketinggian node dan tidak lebih dari dua operasi rotasi. Gabungkan semuanya menjadi satu fungsi insert. Ini akan berbeda dari insert dasar hanya setelah simpul baru fix_insertion!() , yang berpindah dari node yang baru dimasukkan ke root, memeriksa dan, jika perlu, mengoreksi keseimbangan.

 function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 # true == 1, false == 0 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

Fungsi fix_insertion!() Memeriksa perbedaan ketinggian antara dua simpul anak, mulai dari simpul induk dari yang dimasukkan. Jika sama dengan 1 - kita berada dalam kasus 1, Anda perlu menaikkan ketinggian node dan pergi lebih tinggi. Jika nol, pohon seimbang. Jika sama dengan 2 - ini adalah kasus 2 atau 3, Anda perlu menerapkan rotasi yang sesuai, dan pohon mencapai kondisi seimbang.

 #     -  , #   -  imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) #      0 - ..        while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 #       , # ..   dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end 

Hapus catatan

Menghapus sedikit lebih sulit daripada memasukkan.

Untuk memulai, pertimbangkan penghapusan entri dari pohon pencarian biner yang biasa.

1. Jika catatan yang dihapus ada di lembar, maka catatan itu hanya dihapus, semuanya sederhana di sini.
2. Jika catatan yang dihapus berada dalam node yang hanya memiliki satu keturunan, maka keturunan ini, bersama dengan semua subtree-nya, diletakkan di tempat node jarak jauh.
3. Jika ada dua keturunan, maka elemen maksimum dicari di subtree kiri, atau minimum di kanan, diekstraksi dari pohon (oleh properti pohon pencarian, node dengan elemen maksimum dijamin tidak memiliki keturunan kanan, dan dengan elemen minimum ke kiri, jadi penghapusan ini mudah) dan menempatkan catatan yang dihapus.

Tetapi setelah itu, keseimbangan pohon mungkin terganggu, jadi Anda harus naik dari induk dari simpul jarak jauh, memulihkannya. Perhatikan bahwa pada awalnya dijamin bahwa salah satu keturunan dari orang tua yang dimaksud mengurangi ketinggian dengan 1. Dengan mempertimbangkan hal ini, Anda perlu mempertimbangkan opsi (node ​​yang mengubah ketinggian ditunjukkan dengan warna merah, simpul yang diproses adalah induk dari merah):

Kasus 1
Ketidakseimbangan nol. Jadi, sebelum dihapus, itu adalah 1 modulo, dan sekarang simpul anak 2 lebih rendah dari induknya.

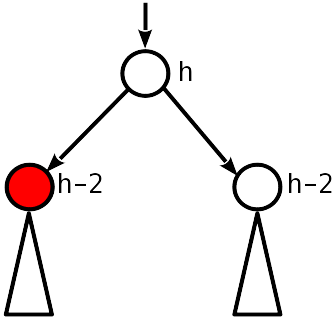
Anda harus menurunkan simpul induk sebanyak 1 dan terus bergerak ke atas.

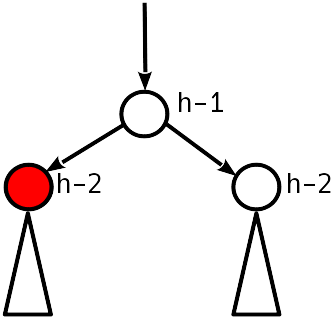
Kasus 2
Ketidakseimbangan 1 modulo.

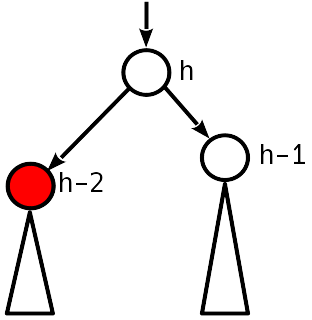
Kondisi AVL puas, Anda bisa berhenti.

Kasus 3
Ketidakseimbangan 2 adalah modulo, simpul saudara ke simpul turun memiliki ketidakseimbangan yang tidak nol.

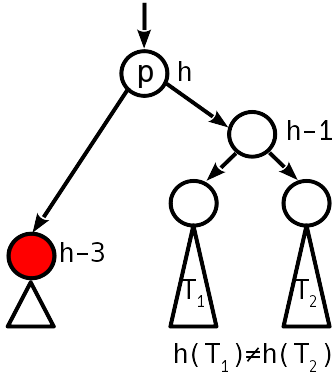
Kami mengembalikan keseimbangan dengan sederhana (jika T1 lebih rendah dari T2) atau dengan menggandakan (jika tidak) rotasi, seperti yang dilakukan selama penyisipan. Ketinggian subtree berkurang, mis. pelanggaran dapat terjadi di atas pohon.

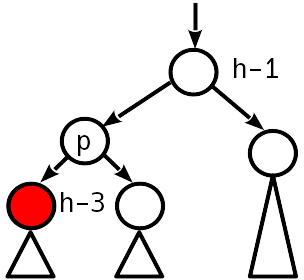
Kasus 4
Ketidakseimbangan 2 modulo, simpul saudara memiliki nol ketidakseimbangan.

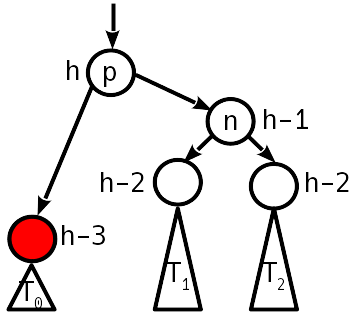
Rotasi sederhana mengembalikan kondisi keseimbangan, sedangkan ketinggian subtree tidak berubah - kami berhenti bergerak ke atas.

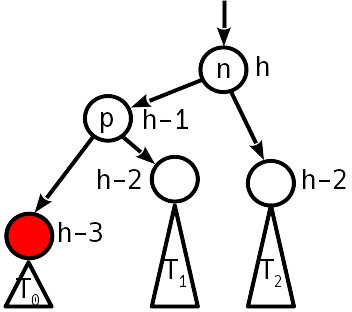
 function next_node(node::AVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::AVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::AVLNode) node = start skew = imbalance(node) while (node !== node.parent) && (abs(skew) != 1) if skew != 0 @assert abs(skew) == 2 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) < 2 if prev_skew == dir node = double_rotate!(child(n, dir), dir) else node = rotate!(n, dir) prev_skew != 0 || break end else node.height -= 1 end node = node.parent skew = imbalance(node) end end 

Naik turunnya pohon AVL

Fitur yang tidak terlalu bagus dari pohon AVL klasik adalah kesulitan menghapus catatan: rotasi dapat "mengatur ulang" seluruh subtree satu tingkat ke bawah, maka dalam kasus terburuk, menghapus memerlukan rotasi pohon O (log ₂ N ) - setiap kali Anda naik satu tingkat di fix_deletion!() .

Karena perilaku asimptotik yang tidak begitu baik ini, pohon AVL memberi jalan kepada pohon merah-hitam yang muncul pada tahun 1970-an dan memiliki kondisi keseimbangan yang lebih lemah - jalur dari akar ke daun terjauh tidak lebih dari dua kali jalur dari akar ke daun terdekat. Karena itu, ketinggian pohon merah-hitam dalam kasus terburuk 2log ₂ N versus 1.44log ₂ N untuk pohon AVL, tetapi menghapus catatan tidak memerlukan lebih dari tiga rotasi sederhana. Dengan demikian, pencarian dan penyisipan karena tinggi pohon yang lebih tinggi berpotensi kehilangan kinerja, tetapi ada keuntungan potensial jika penyisipan sering diselingi dengan penghapusan.

AVL menyerang balik

Ternyata algoritma "ideal" untuk membangun pohon pencarian biner harus menjamin ketinggian kecil (pada tingkat pohon AVL klasik) dan jumlah rotasi konstan baik ketika menambah atau menghapus catatan. Ini belum ditemukan, tetapi pada 2015 sebuah karya diterbitkan yang mengusulkan struktur yang meningkatkan sifat-sifat AVL dan pohon merah-hitam. Idenya terletak lebih dekat ke pohon AVL, tetapi kondisi keseimbangan santai untuk memungkinkan penghapusan catatan yang lebih efisien. Sifat-sifat struktur yang disebut "pohon AVL lemah" (W (eak) pohon AVL) dirumuskan sebagai berikut:

1. Pemesanan: untuk setiap simpul, kunci di bagian atas subtree kiri kurang dari kunci di bagian atas subtree kanan (jika turunannya bukan node kosong).
2. Pangkat naik. Setiap node diberi peringkat. Pangkat semua node kosong adalah nol, pangkat lembaran adalah 1. Pangkat simpul orangtua secara ketat lebih besar dari pangkat anak.
3. Lemah ABL-balance: pangkat suatu simpul berbeda dari pangkat simpul anak dengan tidak lebih dari 2.

Ternyata struktur seperti itu termasuk properti dari kedua pohon AVL klasik dan pohon merah-hitam. Secara khusus, jika kami memperkenalkan kondisi bahwa kedua node anak tidak dapat berbeda dari orang tua di peringkat oleh 2, kami mendapatkan pohon AVL biasa, dan peringkat tersebut akan sama persis dengan ketinggian subtree.

Keindahan pohon SAVL adalah bahwa sedikit melemahnya kondisi AVL memungkinkan pohon untuk menjadi seimbang ketika menghapus catatan dengan tidak lebih dari dua putaran! Perkiraan tinggi pohon adalah h <min (1,44 log ₂ M , 2log ₂ N ), di mana N adalah jumlah entri di pohon, M adalah jumlah sisipan, dibandingkan dengan h < ₂ log ₂ N untuk pohon merah-hitam. , - , , .

- , . - .

.

-, "" "". , :

 mutable struct WAVLNode rank::UInt8 key::K value::V left::Union{Nothing, WAVLNode{K,V}} right::Union{Nothing, WAVLNode{K,V}} parent::WAVLNode{K,V} #   function WAVLNode{K,V}() where {K,V} node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing return node end #    - function WAVLNode{K,V}(key, value) where {K,V} key, value = convert(K, key), convert(V, value) node = new{K,V}() node.rank = 1 node.parent = node node.left = node.right = nothing node.key, node.value = key, value return node end end struct WAVLTree{K, V} entry::WAVLNode{K,V} WAVLTree{K,V}() where {K,V} = new{K,V}(WAVLNode{K,V}()) end function child(root::WAVLNode, side::Signed) if side == -1 root.left elseif side == 1 root.right else throw(ArgumentError("Expecting side=-1 to get the left child or side=1 to get the right child")) end end function Base.getindex(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) node = avlt.entry.left while node != nothing key == node.key && return node.value node = (key < node.key ? node.left : node.right) end throw(KeyError(key)) end 

, -. : 1 , — , 0 ( ) 1 ( ). imbalance() , , .

 wavlrank(node::Union{Nothing,WAVLNode}) = node == nothing ? 0 : Int(node.rank) function imbalance(node::WAVLNode) rr, lr = wavlrank(node.right), wavlrank(node.left) skew = rr - lr diff = node.rank - max(rr, lr) skew, diff end 

, . , , , , -, - .

 # pivot       function rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) p = pivot.parent g = p.parent p.height = avlheight(child(pivot, dir)) + 1 pivot.height = p.height + 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) c = child(pivot, dir) #  c  p insert_child!(p, c, -dir) #  p  pivot insert_child!(pivot, p, dir) pivot end # pivot       function double_rotate!(pivot::AVLNode, dir::Signed) dir in (-1, 1) || throw(ArgumentError("Unknown rotation direction")) n = pivot.parent p = n.parent g = p.parent pivot.height = n.height n.height = p.height = pivot.height - 1 # "" pivot  g pivot.parent = g g.left === p && (g.left = pivot) g.right === p && (g.right = pivot) t2, t3 = child(pivot, -dir), child(pivot, dir) #  n  pivot  t2  n insert_child!(n, t2, dir) insert_child!(pivot, n, -dir) #  p  pivot  t3  p insert_child!(p, t3, -dir) insert_child!(pivot, p, dir) pivot end imbalance(node::AVLNode) = avlheight(node.right) - avlheight(node.left) function fix_insertion!(start::AVLNode) node = start.parent skew = imbalance(node) while abs(skew) == 1 node.height += 1 node = node.parent skew = imbalance(node) end @assert abs(skew) == 2 || skew == 0 if skew != 0 dir = -skew ÷ 2 n = child(node, -dir) prev_skew = imbalance(n) @assert abs(prev_skew) == 1 if prev_skew == dir double_rotate!(child(n, dir), dir) else rotate!(n, dir) end end end function Base.setindex!(avlt::AVLTree{K,V}, val, key) where {K,V} key, value = convert(K, key), convert(V, val) parent = avlt.entry.left #   -     if parent == nothing newnode = AVLNode{K,V}(key, value) newnode.parent = avlt.entry avlt.entry.left = avlt.entry.right = newnode return val end key_found = false while !key_found key_found = key == parent.key if key_found parent.value = value else side = (key > parent.key) * 2 - 1 next = child(parent, side) if next == nothing newnode = AVLNode{K,V}(key, value) insert_child!(parent, newnode, side) fix_insertion!(newnode) key_found = true else parent = next end end end return val end 

, — -. .

0
, ..:

1. 1, 1
2. 0, 2 , .
   .

1
2 ( 0, 2 ).
1 .

2
1, 2.

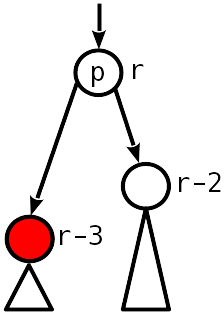
1, .

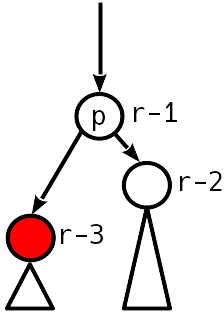
3
2 ( 1, .. ), 2 .

, . .

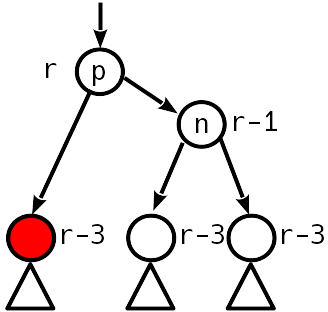
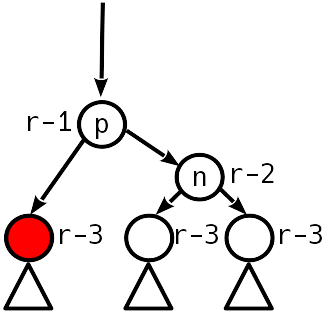
4

.

, , , .. .

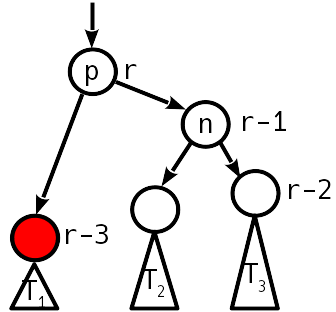
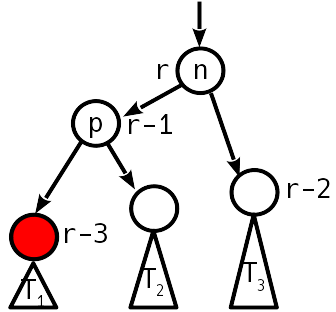
— T ₁ T ₂ , p 2, p 1.

5

.

, , .

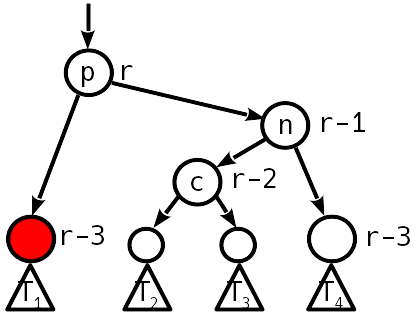
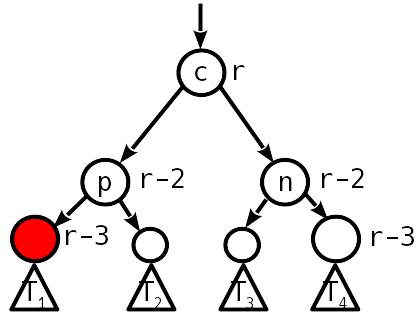
 function next_node(node::WAVLNode) next = node.right if next == nothing p = node.parent next = p.parent while (next !== p) && (next.key < p.key) p, next = next, next.parent end return (next === p ? nothing : next) else while next.left != nothing next = next.left end return next end end function Base.delete!(avlt::WAVLTree{K,V}, key) where {K,V} key = convert(K, key) candidate = avlt.entry.left dir = 0 while candidate.key != key dir = 2 * (key > candidate.key) - 1 candidate = child(candidate, dir) candidate == nothing && return end val = candidate.value for side in (-1, 1) if child(candidate, side) == nothing p, s = candidate.parent, child(candidate, -side) if p === p.parent insert_child!(p, s, 1) insert_child!(p, s, -1) else insert_child!(p, s, dir) fix_deletion!(p) end return end end swap = next_node(candidate) cp, sp, sr = candidate.parent, swap.parent, swap.right swap.height = candidate.height insert_child!(swap, candidate.left, -1) for side in (-1, 1) child(cp, side) === candidate && insert_child!(cp, swap, side) end if sp === candidate fix_deletion!(swap) else insert_child!(swap, candidate.right, 1) insert_child!(sp, sr, -1) fix_deletion!(sp) end return end function fix_deletion!(start::WAVLNode) node = start skew, diff = imbalance(node) while (node !== node.parent) if skew == 0 if node.right == nothing node.rank = 1 else break end elseif abs(skew) == 1 if diff == 1 break else node.rank -= 1 end else dir = -skew ÷ 2 n = child(node, -dir) prev_skew, prev_diff = imbalance(n) if prev_diff == 2 @assert prev_skew == 0 n.rank -= 1 node.rank -= 1 elseif prev_skew == dir double_rotate!(child(n, dir), dir) break else rotate!(n, dir) break end end node = node.parent skew, diff = imbalance(node) end end 

-.

 julia> const wavl = WAVLTree{Int, Int}() julia> const avl = AVLTree{Int, Int}() julia> const dd = Dict{Int,Int}() julia> x = trues(1_000_000) #       ~  julia> for i = 1:1_000_000; dd[i] = avl[i] = wavl[i] = i * i; end julia> for i=1:500_000 k = rand(1:1_000_000) x[k] = false delete!(avl, k) delete!(wavl, k) delete!(dd, k) end # ,     julia> const y = Int[] julia> for i in eachindex(x); if x[i] push!(y, i); end; end julia> @btime let s = 0.0; for idx in y; s += dd[idx]; end; s; end 57.626 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += wavl[idx]; end; s; end 57.796 ms (0 allocations: 0 bytes) 2.0238199367708794e17 julia> @btime let s = 0.0; for idx in y; s += avl[idx]; end; s; end 53.884 ms (0 allocations: 0 bytes) 2.0238199367708794e17 

, , . , , - , -, .

— ?
— , . , , .

.

— , . n - . , , .. , .

*

— , " ", " ", " -", " ". , , -. . , .

*
** O (1), ...

, " — ". , . — ( ) , , , . .

*
** ,

Kesimpulan

() — , , , , , . — , .. , , .

Referensi

1. "-" nickme
2. Rank-Balanced Trees by Bernhard Haeupler, Siddhartha Sen, Robert E. Tarjan // ACM Transactions on Algorithms | June 2015, Vol 11(4) pdf
3. Goodrich MT, Tamassia R. Algorithm Design and Applications