Saya menemukan
artikel yang bagus tentang metode estimasi spektral, yang bagus untuk sinyal pendek dari jumlah harmonik low-noise.
(-copy) Mungkin komentar saya akan membantu pembaca memahami esensi dari metode ini. Yang membuat saya sedikit kesal adalah kemampuan metode yang diimplementasikan secara tidak lengkap. Metode ini digunakan untuk radar - untuk dengan cepat menentukan arah sinyal yang masuk (sudut θ) dengan tujuan otomatis berikutnya, harus dipahami, adaptasi sistem. Tetapi - penulis tidak menghasilkan definisi numerik dari sudut ini (dan ini aneh dalam konteksnya), meskipun definisi ini sangat mungkin. Kami hanya memiliki grafik yang indah, yang menurutnya ternyata, sistem masih perlu "merangkak" dan "merangkak", menentukan jumlah dan lokasi maxima, yang tidak sepenuhnya baik.
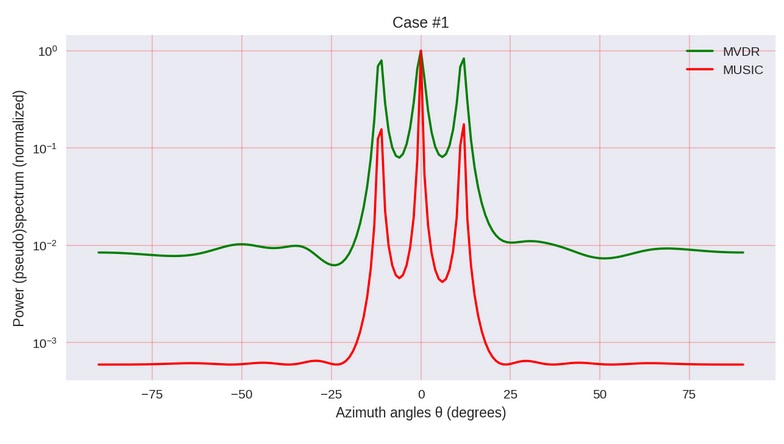Ilustrasi penulis artikel yang disebutkan"Pernyataan masalah"
Singkatnya: kita perlu menentukan di mana (pada sudut apa) sinyal berasal dari antena teralis. Kemudian untuk menyesuaikan ke arah - tetapi ini tidak lagi dalam "lagu" ini.
“Memodelkan sinyal yang diterima”
(itu tidak penting - rupanya, "simbol" harus dibaca di mana-mana sebagai "sinyal")
Di sini, hati-hati. Penulis tampaknya bekerja dengan sinyal kompleks tertentu (spasial). Meskipun
X , ya, bisa, seperti yang tertulis, matriks "amplitudo kompleks" (tidak tergantung pada koordinat, tetapi pada frekuensi spasial), tetapi, misalnya,
XX H adalah "kovariansi" dan bukan "kepadatan spektral".
S lebih mirip dengan matriks "amplitudo kompleks", dengan bantuan komponen harmonik (sinyal berguna) dimodelkan. Tidak ada suara tambahan, atau, tampaknya, bahkan komponen harmonik adalah sinyal analitik di sini. Meskipun harmonik, dengan pemesanan, sangat dekat dengan ini.
"# Formula umum:
# sqrt (N0 / 2) * (G1 + jG2),
# di mana G1 dan G2 adalah proses Gaussian independen. "
Yang utama adalah dari mana komponen imajiner berasal dari pengukuran nyata, entah bagaimana itu tidak jelas. Pada prinsipnya, dimungkinkan untuk menghitung sinyal analitis.
Ada kemungkinan bahwa ada "sumber" di mana mereka bekerja dengan
X nyata (sinyal yang diterima). Sebagai contoh, penulis, tampaknya, sangat tertarik untuk “membuat” spektrum yang dihasilkan simetris (datar) - dalam semua kasus yang dipertimbangkan, sinyal uji diberikan secara simetris ke kiri dan kanan.
"Ketentuan"
Kami menentukan rentang sudut θ kedatangan sinyal, di mana masuk akal untuk melihat. Benar, lalu kami membuat grafik untuk beberapa alasan dari +90 hingga -90 derajat.
“Sedikit teori tentang metode itu sendiri”
Selain itu. MUSIK diperoleh dari
estimasi autoregresif (dari persamaan Yule-Walker) hampir dengan sendirinya, dalam kasus di mana varian white noise bersyarat diabaikan. Hasilnya hampir sama. Solusi SLAE bahkan sedikit lebih ekonomis daripada pencarian vektor eigen, tetapi, karena beberapa alasan, dekomposisi spektral dari matriks kovarians dengan kondisionalitasnya yang buruk akan sangat diinginkan dengan cara apa pun.
Sebenarnya, EVD hanyalah = "menemukan nilai eigen dan vektor", dan tidak lebih. Bukan algoritma.
Mengapa kita menulis "pseudo-spectrum" - karena spektrum hanya dapat ditentukan dari vektor eigen dari matriks kovarians (korelasi) hanya hingga faktor skala, mis. nilai absolut yang dihasilkan tidak masuk akal. Tetapi kita hanya membutuhkan posisi maksimal dan maksimal saja.
- Ini yang paling menarik. Yah, pertama, U
0 sudah vektor eigen, hanya untuk matriks kovarians - dan "simpan" pada pencarian mereka akan gagal. Selanjutnya Pencarian solusi akan mengarah pada kebutuhan untuk menentukan akar dari persamaan daya, yang benar-benar setara dengan dekomposisi spektral lain. Penulis, tampaknya, membingungkan nilai eigen dari matriks yang sama sekali berbeda.
Tapi ... hal utama ... sekarang (!), Akhirnya (!), Kita bisa logaritma akar dan secara numerik menentukan "impedansi" kompleks (model kutub) (dalam persamaan, ini lagi θ, yang tidak terlalu baik), yang bagian imajiner mereka akan menunjukkan sudut ini di mana sinyal datang. Sangat disayangkan penulis tidak melakukannya.
"Pemodelan"
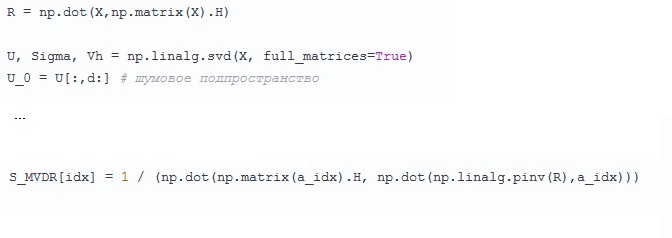
Berikut ini sedikit mengkhawatirkan - pada awalnya matriks kovarian
R =
XX H dihitung, yang karena alasan tertentu dilupakan untuk beberapa waktu dan mulai dari awal lagi - diuraikan menjadi bilangan singular dan vektor
X. Mereka berjanji melalui teks untuk mencari nilai eigen dan vektor R, yang, tentu saja, sama, tetapi karena lebih logis, ketika R telah ditemukan. Tidak jelas masalah apa yang ditemui penulis.
Kami mengingat
R ketika kami mengevaluasi spektrum menggunakan metode dispersi minimum MVDR. Dan di sini juga menarik -
R , dilihat dari naskahnya, tampaknya telah dibalik, sesuai sepenuhnya dengan metode ini, dengan cara klasik, tanpa SVD (inversi semu), meskipun tampaknya berperingkat rendah (sangat berdegenerasi). Maksudku, apakah suara kita begitu kecil? Yah, mungkin.
Sangat membingungkan disini. Ukuran "subruang noise" dalam skrip tampaknya ditetapkan oleh urutan kehendak (sama dengan d). Tetapi dalam kasus sebenarnya, kami tidak tahu berapa banyak harmonisa yang ada dalam sinyal, dan berapa banyak suara. Itu perlu untuk menganalisis nilai-nilai eigen ini - yang mana dari mereka sangat kecil, yang tidak.
Secara umum, pekerjaannya sangat menarik, dan tidak hanya untuk radar. Metode ini, saya percaya, memiliki potensi besar, hanya untuk jenis sinyal ini. Penulis bekerja dengan sangat baik, dan beberapa inkonsistensi yang mengganggu tidak begitu sulit untuk diperbaiki. Dan yang utama adalah melengkapi artikel dengan metode RootMUSIC.