Jika Anda tidak menulis program, jangan gunakan bahasa pemrograman

Leslie Lamport adalah penulis karya mendasar dalam komputasi terdistribusi, dan Anda juga dapat mengenalnya melalui huruf La di La TeX - “Lamport TeX”. Ini adalah pertama kalinya ia memperkenalkan konsep konsistensi yang konsisten pada tahun 1979, dan artikelnya “Bagaimana Membuat Komputer Multiprosesor yang Menjalankan Program Multiproses dengan Benar” memenangkan Hadiah Dijkstra (lebih tepatnya, pada tahun 2000 hadiah itu disebut dengan cara lama: “PODC Influential Paper Award) "). Ada sebuah artikel di Wikipedia tentang dia di mana Anda bisa mendapatkan beberapa tautan yang lebih menarik. Jika Anda senang memecahkan masalah yang terjadi sebelum atau masalah para jenderal Bizantium (BFT), maka Anda harus memahami bahwa Lamport berada di balik semua ini.

Habrastatia ini adalah terjemahan dari laporan Leslie di Heidelberg Laureate Forum pada tahun 2018. Pembicaraan akan fokus pada metode formal yang digunakan dalam mengembangkan sistem yang kompleks dan kritis seperti wahana antariksa Rosetta atau mesin Amazon Web Services. Melihat laporan ini adalah suatu keharusan untuk sesi tanya jawab yang akan diadakan Leslie di Hydra Conference - habrastatia ini dapat menghemat satu jam waktu menonton video. Pada pengantar ini selesai, kami sampaikan kata kepada penulis.

Sekali waktu, Tony Hoar menulis: "Setiap program besar memiliki program kecil yang mencoba keluar." Saya akan ulangi seperti ini: "Di setiap program besar, ada algoritma yang mencoba keluar." Namun, saya tidak tahu apakah Tony akan setuju dengan interpretasi seperti itu.

Pertimbangkan, sebagai contoh, algoritma Euclidean untuk menemukan pembagi umum terbesar dari dua bilangan bulat positif $$$(M, N)$ . Dalam algoritma ini kami tetapkan $$$x$ nilai $$$M$ , $$$N$ - nilai $$$y$ , dan kemudian kurangi nilai terkecil dari nilai terbesar ini, hingga sama. Arti ini $$$x$ dan $$$y$ dan akan menjadi faktor umum terbesar. Apa perbedaan penting antara algoritma ini dan program yang mengimplementasikannya? Dalam program semacam itu akan ada banyak hal tingkat rendah: $$$M$ dan $$$N$ akan ada tipe tertentu, BigInteger atau semacamnya; akan perlu untuk menentukan perilaku program jika $$$M$ dan $$$N$ tidak positif; dan seterusnya dan seterusnya. Tidak ada perbedaan yang jelas antara algoritma dan program, tetapi pada level intuitif kami merasakan perbedaannya - algoritma lebih abstrak, level lebih tinggi. Dan, seperti yang saya katakan, di dalam setiap program tinggal sebuah algoritma yang mencoba untuk keluar. Biasanya ini bukan algoritma yang kami diberitahu tentang kursus algoritma. Sebagai aturan, ini adalah algoritma yang hanya berguna untuk program khusus ini. Paling sering, itu akan jauh lebih rumit daripada yang dijelaskan dalam buku. Algoritma seperti ini sering disebut spesifikasi. Dan dalam kebanyakan kasus, algoritma ini gagal keluar, karena programmer tidak mencurigai keberadaannya. Faktanya adalah bahwa algoritma ini tidak dapat dilihat jika pemikiran Anda terfokus pada kode, pada tipe, pengecualian, while loop, dan banyak lagi, dan bukan pada sifat matematika angka. Suatu program yang ditulis dengan cara ini sulit untuk di-debug, jadi apa artinya melakukan debug algoritma pada level kode. Alat debugging dirancang untuk menemukan kesalahan dalam kode, dan bukan dalam algoritma. Selain itu, program semacam itu tidak akan efektif, karena, sekali lagi, Anda akan mengoptimalkan algoritme pada tingkat kode.

Seperti di hampir semua bidang sains dan teknologi lainnya, masalah-masalah ini dapat diselesaikan dengan menggambarkannya secara matematis. Ada banyak cara untuk melakukan ini, kami akan mempertimbangkan yang paling berguna dari mereka. Ia bekerja dengan algoritma sekuensial dan paralel (terdistribusi). Metode ini terdiri dalam menggambarkan eksekusi algoritma sebagai urutan negara, dan setiap negara sebagai penugasan properti ke variabel. Sebagai contoh, algoritma Euclidean digambarkan sebagai urutan keadaan berikut: pertama, x diberikan nilai M (angka 12), dan y adalah nilai N (angka 18). Kemudian kita kurangi nilai yang lebih kecil dari yang lebih besar ( $$$x$ dari $$$y$ ), yang membawa kita ke keadaan selanjutnya di mana kita sudah mengambil $$$y$ dari $$$x$ , dan eksekusi algoritma berhenti pada ini: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ .

Kami menyebut urutan perilaku status dan sepasang status berturut-turut sebagai langkah. Kemudian algoritma apa pun dapat dijelaskan oleh berbagai perilaku yang mewakili semua varian algoritma yang mungkin. Untuk setiap M dan N tertentu, hanya ada satu perwujudan, oleh karena itu, satu set perilaku cukup untuk menggambarkannya. Algoritma yang lebih kompleks, terutama yang paralel, memiliki banyak perilaku.

Banyak perilaku dijelaskan, pertama, dengan predikat awal untuk status (predikat hanyalah fungsi dengan nilai Boolean); dan, kedua, predikat negara bagian berikutnya untuk pasangan negara. Beberapa perilaku $$$s_1, s_2, s_3 ...$ memasuki banyak perilaku hanya jika predikat awal berlaku untuk $$$s_1$ , dan predikat negara bagian berikutnya adalah benar untuk setiap langkah $$$(s_i, s_ {i + 1})$ . Mari kita coba gambarkan algoritma Euclidean dengan cara ini. Predikat awal di sini adalah: $$$(x = M) \ tanah (y = N)$ . Dan predikat negara bagian berikutnya untuk pasangan negara dijelaskan oleh rumus berikut:

Tolong jangan khawatir - hanya ada enam baris di dalamnya; sangat mudah untuk mengetahuinya jika Anda melakukan ini secara berurutan. Dalam rumus ini, variabel tanpa stroke merujuk ke status pertama, dan variabel dengan stroke adalah variabel yang sama di status kedua.

Seperti yang Anda lihat, baris pertama mengatakan bahwa dalam kasus pertama x lebih besar dari y di negara pertama. Setelah AND logis, dinyatakan bahwa nilai x di negara kedua sama dengan nilai x di negara pertama dikurangi nilai y di negara pertama. Setelah logika AND lainnya, dinyatakan bahwa nilai y pada status kedua sama dengan nilai y pada status pertama. Semua ini berarti bahwa dalam kasus ketika x lebih besar dari y, program akan mengurangi y dari x dan membiarkan y tidak berubah. Tiga baris terakhir menggambarkan kasus ketika y lebih besar dari x. Perhatikan bahwa rumus ini salah jika x sama dengan y. Dalam hal ini, tidak ada status berikutnya, dan perilaku berhenti.

Jadi, kami baru saja menggambarkan algoritma Euclidean dalam dua rumus matematika - dan kami tidak perlu mengacaukan dengan bahasa pemrograman apa pun. Apa yang bisa lebih indah dari dua formula ini? Gantilah dengan satu formula. Perilaku $$$s_1, s_2, s_3 ...$ adalah eksekusi algoritma Euclidean hanya jika:

• $$$Init_E$ berlaku untuk $$$s_1$ ,
• $$$Next_E$ berlaku untuk setiap langkah $$$(s_i, s_ {i + 1})$ .

Ini dapat ditulis sebagai predikat untuk perilaku (kami akan menyebutnya properti) sebagai berikut. Kondisi pertama dapat dinyatakan hanya sebagai $$$Init_E$ . Ini berarti bahwa kami menafsirkan predikat keadaan sebagai benar untuk perilaku hanya jika itu benar untuk keadaan pertama. Kondisi kedua ditulis sebagai berikut: $$$\ square Next_E$ . Kuadrat berarti korespondensi antara predikat pasangan negara dan predikat perilaku, mis. $$$Next_E$ berlaku untuk setiap langkah dalam perilaku. Hasilnya, rumusnya terlihat seperti ini: $$$Init_E \ land \ square Next_E$ .

Jadi, kami menulis algoritma Euclidean secara matematis. Intinya, ini hanyalah definisi, atau singkatan $$$Init_E$ dan $$$Next_E$ . Seluruh rumus ini akan terlihat seperti ini:

Bukankah dia cantik? Sayangnya, untuk sains dan teknologi, kecantikan bukanlah kriteria penentu, tetapi itu berarti bahwa kita berada di jalur yang benar.

Properti yang kami catat berlaku untuk beberapa perilaku hanya jika dua kondisi yang baru saja kami jelaskan terpenuhi. Di $$$M = 12$ dan $$$N = 18$ mereka berlaku untuk perilaku berikut: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6], [x \ leftarrow 6, \ leftarrow 6]$ . Tetapi kondisi ini juga puas untuk versi yang lebih pendek dari perilaku yang sama: $$$[x \ leftarrow 12, \ leftarrow 18], [x \ leftarrow 12, \ leftarrow 6]$ . Dan kita tidak harus memperhitungkannya, karena ini hanyalah langkah terpisah dari perilaku yang telah kita perhitungkan. Ada cara yang jelas untuk menyingkirkannya: abaikan saja perilaku yang berakhir pada keadaan yang paling tidak satu langkah berikutnya mungkin terjadi. Tetapi ini bukan pendekatan yang tepat, kita membutuhkan solusi yang lebih umum. Selain itu, kondisi ini tidak selalu berhasil.

Diskusi tentang masalah ini membawa kita pada konsep keamanan dan aktivitas. Properti keamanan menunjukkan acara mana yang valid. Misalnya, algoritma diizinkan untuk mengembalikan nilai yang benar. Properti aktivitas menunjukkan peristiwa mana yang harus terjadi cepat atau lambat. Misalnya, suatu algoritma harus mengembalikan beberapa nilai, cepat atau lambat. Untuk algoritma Euclidean, properti keamanan adalah sebagai berikut: $$$Init_E \ land \ square Next_E$ . Properti aktivitas harus ditambahkan ke ini untuk mencegah berhenti prematur: $$$Init_E \ land \ square Next_E \ land L$ . Dalam bahasa pemrograman, paling tidak, ada beberapa definisi primitif kegiatan. Paling sering, kegiatan bahkan tidak disebutkan, itu hanya tersirat bahwa langkah selanjutnya dalam program harus terjadi. Dan untuk menambahkan properti ini, Anda memerlukan kode yang agak rumit. Secara matematis, sangat mudah untuk mengekspresikan aktivitas (hanya persegi itu diperlukan untuk ini), tetapi, sayangnya, saya tidak punya waktu untuk ini - kita harus membatasi diskusi kita untuk keamanan.

Penyimpangan kecil hanya untuk ahli matematika: setiap properti adalah seperangkat perilaku yang sifatnya benar. Untuk setiap rangkaian urutan, ada topologi alami yang dibuat oleh fungsi jarak berikut:

$$$s = 17, \ sqrt {2}, -2, \ pi, 10, 1/2 \\ t = 17, \ sqrt {2}, -2, e, 10, 1/$

Jarak antara kedua fungsi ini adalah ¼, karena perbedaan pertama di antara keduanya adalah pada elemen keempat. Dengan demikian, semakin lama bagian di mana urutan ini identik, semakin dekat mereka satu sama lain. Fungsi ini sendiri tidak begitu menarik, tetapi ia menciptakan topologi yang sangat menarik. Dalam topologi ini, properti keamanan adalah set tertutup, dan properti aktivitas adalah set padat. Dalam topologi, salah satu teorema dasar menyatakan bahwa setiap himpunan adalah persimpangan dari himpunan tertutup dan himpunan padat. Jika kita ingat bahwa properti adalah serangkaian perilaku, maka dari teorema ini bahwa setiap properti adalah gabungan dari properti keamanan dan properti aktivitas. Ini adalah kesimpulan yang akan menarik bagi para programmer juga.

Ketepatan sebagian berarti bahwa program dapat berhenti hanya jika memberikan jawaban yang benar. Sebagian kebenaran dari algoritma Euclidean mengatakan bahwa jika itu menyelesaikan eksekusi, maka $$$x = GCD (M, N)$ . Dan algoritma kami menyelesaikan eksekusi jika $$$x = y$ . Dengan kata lain, $$$(x = y) \ Rightarrow (x = GCD (M, N))$ . Ketepatan sebagian dari algoritma ini berarti rumus ini berlaku untuk semua kondisi perilaku. Tambahkan simbol ke awal $$$\ persegi$ yang berarti "untuk semua langkah." Seperti yang Anda lihat, tidak ada variabel dengan stroke dalam rumus, jadi kebenarannya tergantung pada status pertama pada setiap langkah. Dan jika ada sesuatu yang benar untuk keadaan pertama dari setiap langkah, maka pernyataan ini berlaku untuk semua negara. Kebenaran sebagian dari algoritma Euclidean dipenuhi oleh perilaku yang dapat diterima untuk algoritma tersebut. Seperti yang telah kita lihat, perilaku diperbolehkan jika formula yang baru saja diberikan adalah benar. Ketika kami mengatakan bahwa sebuah properti terpenuhi, itu berarti bahwa properti ini mengikuti dari beberapa formula. Bukankah itu luar biasa? Ini dia:

$$$Init_E \ land \ square Next_E \ Rightarrow \ square ((x = y) \ Rightarrow (x = GCD (M, N)))$

Kami beralih ke invarian. Kotak dengan tanda kurung setelah itu disebut properti invarian :

$$$Init_E \ land \ square Next_E \ Rightarrow \ color {red} {\ square ((x = y) \ Rightarrow (x = GCD (M, N)))}$

Nilai terlampir dalam tanda kurung setelah kuadrat disebut invarian :

$$$Init_E \ land \ square Next_E \ Rightarrow \ square (\ color {red} {(x = y) \ Rightarrow (x = GCD (M, N))})$

Bagaimana cara membuktikan invarian? Untuk membuktikan $$$Init_E \ land \ square Next_E \ Rightarrow \ square I_E$ , Anda perlu membuktikan bahwa untuk perilaku apa pun $$$s_1, s_2, s_3 ...$ konsekuensinya $$$Init_E \ land \ square Next_E$ adalah kebenaran $$$I_e$ untuk kondisi apa pun $$$s_j$ . Kita dapat membuktikan ini dengan induksi, untuk ini kita perlu membuktikan yang berikut:

1. dari $$$Init_E \ land \ square Next_E$ mengikuti itu $$$I_e$ berlaku untuk negara $$$s_1$ ;
2. dari $$$Init_E \ land \ square Next_E$ karena itu jika $$$I_e$ berlaku untuk negara $$$s_j$ maka itu juga
   berlaku untuk negara $$$s_ {j + 1}$ .

Pertama, kita perlu membuktikannya $$$Init_E$ tersirat $$$I_e$ . Karena formula mengklaim itu $$$Init_E$ benar untuk keadaan pertama, ini artinya $$$I_e$ berlaku untuk kondisi pertama. Selanjutnya, kapan $$$Next_E$ berlaku untuk setiap langkah, dan $$$I_e$ setia pada $$$s_j$ , $$$I_e$ berlaku untuk $$$s_ {j + 1}$ karena $$$\ square Next_E$ berarti itu $$$Next_E$ berlaku untuk setiap pasangan negara. Ini ditulis seperti ini: $$$Next_E \ land I_E \ Rightarrow I'_E$ dimana $$$I'_E$ Apakah itu $$$I_e$ untuk semua variabel dengan stroke.

Invarian yang memenuhi dua kondisi yang baru saja kami buktikan disebut invarian induktif . Kebenaran sebagian tidak induktif. Untuk membuktikan invariannya, Anda perlu menemukan invarian induktif yang menyiratkannya. Dalam kasus kami, invarian induktif adalah sebagai berikut: $$$GCD (x, y) = GCD (M, N)$ .

Setiap tindakan selanjutnya dari algoritma tergantung pada kondisi saat ini, dan bukan pada tindakan sebelumnya. Algoritma ini memenuhi properti keamanan, karena invarian induktif dipertahankan di dalamnya. Algoritma Euclidean dapat menghitung common denominator terbesar (mis., Tidak berhenti sampai tercapai) karena fakta bahwa ia memiliki invarian $$$GCD (x, y) = GCD (M, N)$ . Untuk memahami algoritme, Anda perlu mengetahui invarian induktifnya. Jika Anda mempelajari verifikasi program, maka Anda tahu bahwa bukti invarian yang diberikan tidak lebih dari sebuah metode untuk membuktikan kebenaran parsial program Floyd-Hoare berurutan. Anda mungkin juga pernah mendengar tentang metode Hoviki - Gris , yang merupakan perluasan dari metode Floyd-Hoar ke program paralel. Dalam kedua kasus, invarian induktif ditulis menggunakan anotasi program. Dan jika Anda melakukan ini dengan bantuan matematika, dan bukan dengan bahasa pemrograman, ini dilakukan dengan sangat sederhana. Inilah yang menjadi inti metode Oviki-Gris. Matematika membuat fenomena kompleks jauh lebih mudah diakses untuk dipahami, meskipun fenomena itu sendiri, tentu saja, tidak akan menjadi lebih sederhana.

Lihatlah formula ini lebih dekat. Jika dalam matematika kita menulis rumus dengan variabel $$$x$ dan $$$y$ , ini tidak berarti bahwa variabel lain tidak ada. Anda bisa menambahkan persamaan lain di mana $$$y$ ditempatkan sehubungan dengan $$$z$ , itu tidak akan mengubah apa pun. Rumusnya tidak mengatakan apa-apa tentang variabel lain. Saya sudah mengatakan bahwa keadaan adalah penugasan nilai ke variabel, sekarang Anda dapat menambahkan ini: dengan semua variabel yang mungkin, dimulai $$$x$ dan $$$y$ dan diakhiri dengan populasi Iran. Saya harus mengakui: ketika saya mengatakan formula itu $$$Init_E \ land \ square Next_E$ menjelaskan algoritma Euclidean, saya berbohong. Ini sebenarnya menggambarkan alam semesta di mana artinya $$$x$ dan $$$y$ mewakili eksekusi algoritma Euclidean. Bagian kedua dari rumus ( $$$\ square Next_E$ ) mengklaim bahwa setiap langkah berubah $$$x$ atau $$$y$ . Dengan kata lain, ini menggambarkan alam semesta di mana populasi Iran dapat berubah hanya jika artinya telah berubah $$$x$ atau $$$y$ . Oleh karena itu di Iran tidak ada yang bisa dilahirkan setelah eksekusi algoritma Euclidean selesai. Jelas, ini tidak benar. Kesalahan ini dapat diperbaiki jika kami memiliki langkah-langkah yang valid untuk itu $$$x$ dan $$$y$ tetap tidak berubah. Karena itu, kita perlu menambahkan satu bagian lagi ke formula kita: $$$Init_E \ land \ square (Next_E \ lor (x '= x) \ land (y' = y))$ . Untuk singkatnya, kami menulis seperti ini: $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ . Rumus ini menjelaskan alam semesta yang mengandung algoritma Euclidean. Perubahan yang sama harus dilakukan dalam bukti invarian:

• Kami membuktikan: $$$Init_E \ land \ color {red} {\ square [Next_E] _ {<x, y>}} \ Rightarrow \ square I_E$
• Dengan bantuan:
  
  1. $$$Init_E \ Rightarrow I_E$
  2. $$$\ color {red} {\ square [Next_E] _ {<x, y>}} \ land I_E \ Rightarrow I'_E$

Perubahan ini bertanggung jawab atas keamanan algoritme Euclidean, karena sekarang perilaku dimungkinkan di mana nilainya $$$x$ dan $$$y$ jangan berubah. Perilaku ini harus dihilangkan dengan menggunakan properti aktivitas. Ini cukup sederhana, tetapi saya tidak akan membicarakannya sekarang.

Bicara tentang implementasi. Misalkan kita memiliki beberapa jenis mesin yang mengimplementasikan algoritma Euclidean seperti komputer. Ini mewakili angka sebagai array kata-kata 32-bit. Untuk operasi penambahan dan pengurangan yang sederhana, ia membutuhkan banyak langkah, seperti komputer. Jika Anda belum menyentuh aktivitas, maka kita juga bisa membayangkan mesin seperti itu dengan formula $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ . Apa yang kami maksud ketika kami mengatakan bahwa mesin Euclidean mengimplementasikan algoritma Euclidean? Ini berarti bahwa rumus berikut ini benar:

Jangan khawatir, kami sekarang akan memeriksanya secara berurutan. Dikatakan bahwa mesin kami memenuhi beberapa properti ( $$$\ Rightarrow$ ) Properti ini adalah rumus Euclidean. $$$(Init_E \ land \ square [Next_E] _ {<x, y>}$ , titik adalah ekspresi yang mengandung variabel mesin Euclidean, dan $$$DENGAN$ Apakah substitusi. Dengan kata lain, baris kedua adalah rumus Euclidean $$$x$ dan $$$y$ digantikan oleh titik-titik. Dalam matematika, tidak ada notasi yang diterima secara universal untuk substitusi, jadi saya harus membuatnya sendiri. Pada dasarnya, formula Euclidean ( $$$Init_E \ land \ square [Next_E] _ {<x, y>}$ ) Adalah singkatan untuk rumus:

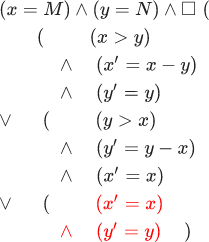
Merah menyorot bagian formula, memungkinkan $$$x$ dan $$$y$ masuk $$$(Init_E \ land \ square [Next_E] _ {\ color {red} {<x, y>}}$ tetap sama.

Ungkapan yang dijelaskan menyatakan tidak hanya bahwa mesin mengimplementasikan algoritma Euclidean, tetapi juga bahwa ia melakukan ini dengan mempertimbangkan penggantian yang ditentukan. Jika Anda hanya mengambil beberapa program dan mengatakan bahwa variabel-variabel dari program ini terkait $$$x$ dan $$$y$ - Tidak masuk akal untuk mengatakan bahwa semua ini "mengimplementasikan algoritma Euclidean." Penting untuk menunjukkan dengan tepat bagaimana algoritma akan diimplementasikan, mengapa, setelah semua permutasi, rumus akan menjadi benar. Sekarang saya tidak punya waktu untuk menunjukkan bahwa definisi yang dijelaskan di atas benar, Anda harus mengambil kata saya untuk itu. Tapi Anda, saya pikir, sudah menghargai betapa sederhana dan elegannya itu. Matematikanya sangat indah - dengan itu kami dapat menentukan apa artinya satu algoritma mengimplementasikan yang lain.

Untuk membuktikan ini, perlu mencari invarian yang cocok $$$I_ {ME}$ Mobil Euclidean. Untuk melakukan ini, kondisi berikut harus dipenuhi:

1. $$$Init_ {ME} \ Rightarrow (Init_E, DENGAN \ thinspace x \ leftarrow ..., y \ leftarrow ...)$
2. $$$I_ {ME} \ land [Next_ {ME}] _ {<...>} \ Rightarrow ([Next_E] _ {<x, y>}, DENGAN \ thinspace x \ leftarrow ..., y \ leftarrow. ..)$

Kami tidak akan menyelidiki mereka sekarang, hanya memperhatikan fakta bahwa ini adalah rumus matematika biasa, meskipun bukan yang paling sederhana. Invarian $$$I_ {ME}$ menjelaskan mengapa mesin Euclidean mengimplementasikan algoritma Euclidean. Implementasi berarti mengganti ekspresi untuk variabel. Ini adalah operasi matematika yang sangat umum. Tetapi dalam program ini, penggantian seperti itu tidak dapat dilakukan. Anda tidak dapat mengganti a + b di tempat x dalam ekspresi penugasan x = … , catatan seperti itu tidak masuk akal. Lalu bagaimana cara menentukan bahwa satu program mengimplementasikan yang lain? Jika Anda hanya berpikir dalam hal pemrograman, ini tidak mungkin. Dalam kasus terbaik, Anda dapat menemukan beberapa definisi rumit, tetapi cara yang jauh lebih baik adalah menerjemahkan program ke dalam rumus matematika dan menggunakan definisi yang saya berikan di atas. Untuk menerjemahkan suatu program ke dalam rumus matematika berarti memberikan program semantik. Jika mesin Euclidean adalah sebuah program, dan $$$Init_ {ME} \ land \ square [Next_ {ME}] _ {<...>}$ - notasi matematika, lalu $$$(Init_E \ land \ square [Next_E] _ {<x, y>}, DENGAN \ thinspace x \ leftarrow ..., y \ leftarrow ...)$ menunjukkan kepada kita bahwa ini berarti bahwa "program mengimplementasikan algoritma Euclidean." Bahasa pemrograman sangat kompleks, jadi terjemahan program ini ke dalam bahasa matematika juga rumit, jadi dalam praktiknya kita tidak. Sederhananya, bahasa pemrograman tidak dirancang untuk menulis algoritma pada mereka. , , , : , x y , . , , , .

- : , , , . , . — . . , . , — , . :

. $$$DecrementX$ :

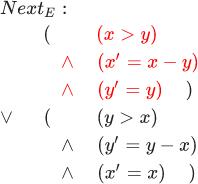
— $$$DecrementY$ :

, :

.

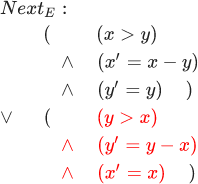
. Rosetta — , . Virtuoso. . TLA+, . , , . , (Eric Verhulst), . , TLA+, : « TLA+ . - C. TLA+ Virtuoso». . . , , , . . TLA+. , .

. Communications of the ACM ] , - Amazon . Amazon Web Services — , Amazon. , — TLA+. . -, , . , , . -, , . , — , , . -, , Amazon , . , 10% TLA+.

— Microsoft. TLA+ 2004 . 2015 TLA+, . . Amazon Web Services. Microsoft , , . : « , ». , Microsoft - . : « ». 2016-17 . TLA+, 150 , Azure ( Microsoft). Azure 2018 , , . : « , . , ». , , . - : , . , , .

, TLA+ . , TLA+, TLA+ Azure, , TLA+. , . , TLA+ , . Microsoft Cosmos DB, , . , . TLA+, , , TLA+.

TLA+ — . . TLA+ . , , . TLA+ , . : TLA+ , .

, . , , . , . Amazon Microsoft , . , .

, . — , . , Hydra 2019, 11-12 2019 -. .