🚷 👨🏿‍🎤 🤶🏽 Penyaringan linear optimal: mulai dari gradient descent hingga filter adaptif 😍 👳🏿 💢

Mengembangkan topik abstrak pada spesialisasi master "Komunikasi dan Pemrosesan Sinyal" (TU Ilmenau), saya ingin melanjutkan salah satu topik utama kursus "Pemrosesan Sinyal Adaptif dan Array" . Yakni, dasar-dasar penyaringan adaptif.

Untuk siapa artikel ini pertama kali ditulis:

1) untuk persaudaraan siswa dengan spesialisasi asli ;
2) untuk guru yang menyiapkan seminar praktis, tetapi belum memutuskan alat - di bawah ini adalah contoh dalam python dan Matlab / Oktaf ;
3) untuk siapa pun yang tertarik dengan topik pemfilteran.

Apa yang dapat ditemukan di bawah potongan:

1) informasi dari teori, yang saya coba atur setepat mungkin, tetapi, menurut saya, secara informatif;
2) contoh penggunaan filter: khususnya, sebagai bagian dari equalizer untuk antena array;
3) tautan ke literatur dasar dan perpustakaan terbuka (dengan python), yang mungkin berguna untuk penelitian.

Secara umum, selamat datang dan mari kita memilah semuanya berdasarkan poin.

Orang termenung dalam foto itu akrab bagi banyak orang, saya pikir, Norbert Wiener. Sebagian besar, kita akan mempelajari filter namanya. Namun, orang tidak dapat gagal untuk menyebut rekan senegaranya - Andrei Nikolaevich Kolmogorov, yang artikelnya tahun 1941 juga memberikan kontribusi signifikan terhadap pengembangan teori penyaringan yang optimal, yang bahkan dalam sumber bahasa Inggris disebut teori penyaringan Kolmogorov-Wiener .

Apa yang sedang kita pertimbangkan?

Hari ini kita sedang mempertimbangkan filter klasik dengan respon impuls terbatas (FIR, respon impuls terbatas), yang dapat dijelaskan oleh rangkaian sederhana berikut (Gbr. 1).

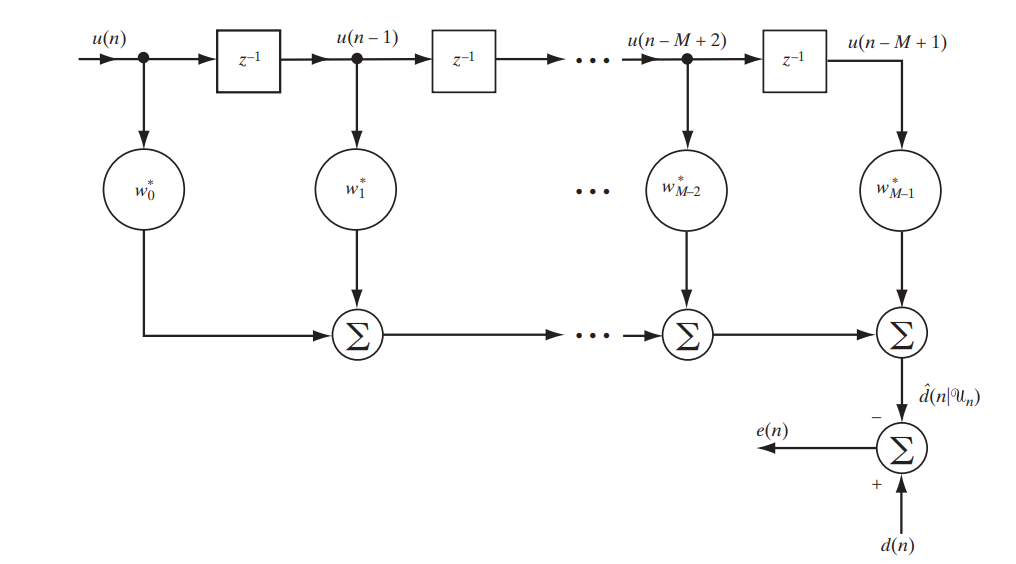
Fig. 1. Skema filter FIR untuk mempelajari filter Wiener. [1. hal.117]

Kami akan menulis dalam bentuk matriks apa yang sebenarnya akan di output dari stand ini:

$e (n) = d (n) - \ hat {d} (n | \ mathcal {U} _n) = d (n) - \ mathbf {w} ^ H \ mathbf {u} \ qquad (1)$

Menguraikan notasi:

Apakah perbedaan (kesalahan) antara sinyal yang diberikan dan yang diterima
Adalah beberapa sinyal yang telah ditetapkan
$\ mathbf {u}$ Apakah vektor sampel atau, dengan kata lain, sinyal pada input filter
$\ hat {d} (n | \ mathcal {U} _n)$ Apakah sinyal pada output filter
$\ mathbf {w} ^ H$ - ini adalah konjugasi Hermitian dari vektor koefisien filter - itu adalah dalam pemilihan optimal mereka bahwa kemampuan beradaptasi dari filter terletak

Anda mungkin sudah menebak bahwa kami akan mengusahakan perbedaan terkecil antara sinyal yang diberikan dan yang difilter, yaitu kesalahan terkecil. Ini berarti bahwa kami menghadapi tugas pengoptimalan.

Apa yang akan kami optimalkan?

Untuk mengoptimalkan, atau lebih tepatnya meminimalkan, kami tidak hanya akan mengartikan galat, galat kuadrat rata - rata ( MSE - Mean Sqared Error ):

$MSE: J (\ mathbf {w}) = E \ {e (n) ^ 2 \} \ qquad (2)$

dimana $J (\ mathbf {w})$ menunjukkan fungsi biaya vektor koefisien filter, dan $E \ {* \}$ menunjukkan tikar. menunggu.

Kuadrat dalam kasus ini sangat menyenangkan, karena itu berarti bahwa kita dihadapkan dengan masalah pemrograman cembung (saya googled hanya analog dari optimasi cembung Inggris), yang, pada gilirannya, menyiratkan satu ekstrem tunggal (dalam kasus kami, minimum).

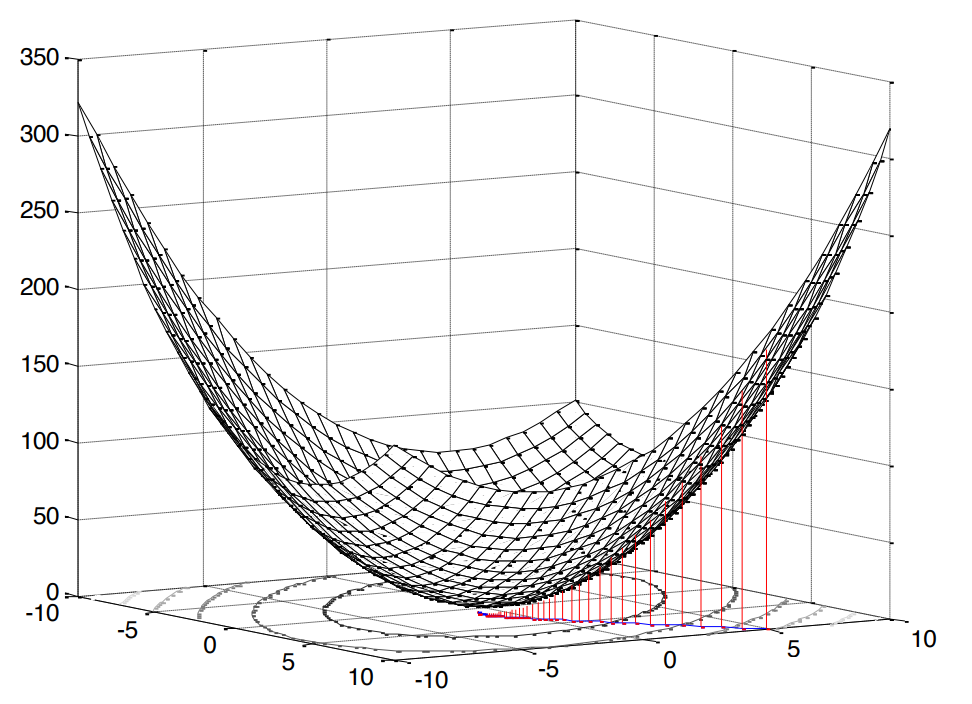
Fig. 2. Permukaan kesalahan kuadrat rata-rata .

Fungsi kesalahan kami memiliki bentuk kanonik [1, hal. 121]:

$J (\ mathbf {w}) = \ sigma ^ 2_d - \ mathbf {w} ^ H \ mathbf {p} - \ mathbf {p} ^ H \ mathbf {w} + \ mathbf {w} ^ H \ mathbf { R} \ mathbf {w} \ qquad (3)$

dimana $\ sigma ^ 2_d$ Apakah varians dari sinyal yang diharapkan, $\ mathbf {p} = E \ {\ mathbf {u} (n) d ^ * (n) \}$ Apakah vektor korelasi silang antara vektor input dan sinyal yang diharapkan, dan $\ mathbf {R} = E \ {\ mathbf {u} (n) \ mathbf {u} ^ H (n) \}$ Merupakan matriks autokorelasi dari sinyal input.

Kesimpulan dari rumus ini ada di sini (saya mencobanya lebih jelas).

Seperti yang kita catat di atas, jika kita berbicara tentang pemrograman cembung, maka kita akan memiliki satu ekstrem (minimum). Jadi, untuk menemukan nilai minimum dari fungsi biaya (kesalahan root mean square kuadrat minimum), cukup untuk menemukan garis singgung dari kemiringan garis singgung atau, dengan kata lain, turunan parsial sehubungan dengan variabel yang kami pelajari:

$\ frac {\ delta J (\ mathbf {w})} {\ delta w ^ *} = - \ mathbf {p} + \ mathbf {R} \ mathbf {w} \ qquad (4)$

Dalam kasus terbaik ( $\ mathbf {w} = \ mathbf {w} _ {opt}$ ), kesalahan harus, tentu saja, minimal, yang berarti kita menyamakan turunannya dengan nol:

$\ mathbf {R} \ mathbf {w} _ {opt} = \ mathbf {p} \ qquad (5)$

Sebenarnya, ini dia, kompor kita, yang darinya kita akan menari lebih jauh: sebelum kita adalah sistem persamaan linear .

Bagaimana kita memutuskan?

Harus segera dicatat bahwa kedua solusi tersebut, yang akan kami pertimbangkan di bawah, dalam hal ini bersifat teoretis dan mendidik $\ mathbf {R}$ dan $\ mathbf {p}$ diketahui sebelumnya (yaitu, kami memiliki kemampuan untuk mengumpulkan statistik yang cukup untuk menghitungnya). Namun, analisis contoh-contoh sederhana di sini adalah yang terbaik yang dapat Anda pikirkan untuk memahami pendekatan dasar.

Solusi analitik

Masalah ini dapat dipecahkan, dengan kata lain, di dahi - menggunakan matriks terbalik:

$\ mathbf {w} _ {opt} = \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (6)$

Ungkapan seperti itu disebut persamaan Wiener - Hopf - masih berguna bagi kita sebagai referensi.

Tentu saja, untuk benar-benar teliti, mungkin akan lebih tepat untuk menuliskan kasus ini secara umum, mis. tidak dengan $^ {-}$ , dan dengan ( balik semu ):
$\ mathbf {R} ^ + = \ mathbf {R} ^ H (\ mathbf {R} \ mathbf {R} ^ H) ^ {- 1}$

Namun, matriks autokorelasi tidak boleh non-kuadrat atau tunggal, oleh karena itu, cukup tepat, kami percaya bahwa tidak ada kontradiksi.

Dari persamaan ini, secara analitik mungkin untuk menyimpulkan berapa nilai minimum dari fungsi biaya akan sama (yaitu, dalam kasus kami MMSE - kesalahan rata-rata kuadrat minimum):

$J_ {min} = J (\ mathbf {w} _ {opt}) = \ sigma ^ 2_d - \ mathbf {p} ^ H \ mathbf {R} ^ {- 1} \ mathbf {p} \ qquad (7)$

Derivasi formula ada di sini (saya juga mencoba membuatnya lebih berwarna).

Nah, ada satu solusi.

Solusi berulang

Namun, ya, adalah mungkin untuk menyelesaikan sistem persamaan linear tanpa membalikkan matriks autokorelasi - secara iteratif ( untuk menghemat perhitungan ). Untuk tujuan ini, pertimbangkan metode gradient descent ( metode gradient descent ) yang asli dan mudah dipahami.

Inti dari algoritma dapat direduksi menjadi sebagai berikut:

Kami menetapkan variabel yang diinginkan ke beberapa nilai default (misalnya, $\ mathbf {w} (0) = \ mathbf {0}$ )
Pilih beberapa langkah $\ mu$ (bagaimana tepatnya kita memilih, kita akan bicara di bawah).
Dan kemudian, seolah-olah, kita turun sepanjang permukaan asli kita (dalam kasus kami, ini adalah permukaan MSE) dengan langkah yang diberikan $\ mu$ dan kecepatan tertentu yang ditentukan oleh besarnya gradien.

Oleh karena itu nama: gradien - gradien atau curam - keturunan selangkah demi selangkah - keturunan.

Gradien dalam kasus kami sudah diketahui: pada kenyataannya, kami menemukannya ketika kami membedakan fungsi biaya (permukaan cekung, bandingkan dengan [1, hal. 220]). Kami menulis bagaimana rumus untuk pembaruan berulang variabel yang diinginkan (koefisien filter) akan terlihat seperti [1, p. 220]:

$\ mathbf {w} (n + 1) = \ mathbf {w} (n) - \ mu [- \ mathbf {p} + \ mathbf {R} \ mathbf {w} (n)] \ qquad (8)$

dimana Apakah nomor iterasi.

Sekarang mari kita bicara tentang memilih ukuran langkah.

Kami daftar tempat yang jelas:

langkah tidak boleh negatif atau nol
langkahnya tidak boleh terlalu besar, jika tidak algoritma tidak akan konvergen (itu akan, seolah-olah, melompat dari ujung ke ujung, tanpa jatuh ke ekstrim)
langkahnya, tentu saja, bisa sangat kecil, tetapi ini juga tidak sepenuhnya diinginkan - algoritma akan menghabiskan lebih banyak waktu

Mengenai filter Wiener, pembatasan, tentu saja, telah ditemukan sejak lama [1, p. 222-226]:

$0 <\ mu <\ frac {2} {\ lambda_ {max}} \ qquad (9)$

dimana $\ lambda_ {maks}$ Merupakan nilai eigen terbesar dari matriks autokorelasi $\ mathbf {R}$ .

Omong-omong, nilai eigen dan vektor adalah topik menarik yang terpisah dalam konteks penyaringan linier. Bahkan ada seluruh filter Eigen untuk kasus ini (lihat Lampiran 1).

Tapi untungnya ini tidak semuanya. Ada juga solusi adaptif yang optimal:

$\ mu (n) = \ frac {\ mathbf {\ gamma} (n) ^ H \ mathbf {\ gamma} (n)} {\ mathbf {\ gamma} (n) ^ H \ mathbf {R} \ mathbf { \ gamma} (n)} \ qquad (10)$

dimana $\ mathbf {\ gamma} (n) = \ mathbf {p} - \ mathbf {R} \ mathbf {w} (n)$ Merupakan gradien negatif. Seperti dapat dilihat dari rumus, langkah dihitung ulang ke dalam setiap iterasi, yaitu, ia beradaptasi.

Kesimpulan rumus ada di sini (banyak matematika - hanya melihat kutu buku terkenal yang sama seperti saya).

Oke, untuk keputusan kedua, kami juga mengatur panggung.

Tetapi apakah mungkin dengan contoh?

Demi kejelasan, kami akan melakukan simulasi kecil. Kami akan menggunakan Python 3.6.4 .

Saya akan segera mengatakan bahwa contoh-contoh ini adalah bagian dari salah satu tugas pekerjaan rumah, yang masing-masing ditawarkan kepada siswa untuk solusi dalam waktu dua minggu. Saya menulis ulang bagian di bawah python (untuk mempopulerkan bahasa di kalangan insinyur radio). Mungkin Anda akan menemukan beberapa opsi lain di Web dari mantan siswa lain.

import numpy as np import matplotlib.pyplot as plt from scipy.linalg import toeplitz def convmtx(h,n): return toeplitz(np.hstack([h, np.zeros(n-1)]),\ np.hstack([h[0], np.zeros(n-1)])) def MSE_calc(sigmaS, R, p, w): w = w.reshape(w.shape[0], 1) wH = np.conj(w).reshape(1, w.shape[0]) p = p.reshape(p.shape[0], 1) pH = np.conj(p).reshape(1, p.shape[0]) MSE = sigmaS - np.dot(wH, p) - np.dot(pH, w) + np.dot(np.dot(wH, R), w) return MSE[0, 0] def mu_opt_calc(gamma, R): gamma = gamma.reshape(gamma.shape[0], 1) gammaH = np.conj(gamma).reshape(1, gamma.shape[0]) mu_opt = np.dot(gammaH, gamma) / np.dot(np.dot(gammaH, R), gamma) return mu_opt[0, 0]

Kami akan menggunakan filter linier kami untuk masalah pemerataan saluran , yang tujuan utamanya adalah untuk meratakan berbagai efek saluran ini pada sinyal yang bermanfaat.

Kode sumber dapat diunduh dalam satu file di sini atau di sini (ya, saya punya hobi - sunting Wikipedia).

Model sistem

Misalkan ada antena array (kami sudah memeriksanya di artikel tentang MUSIK ).

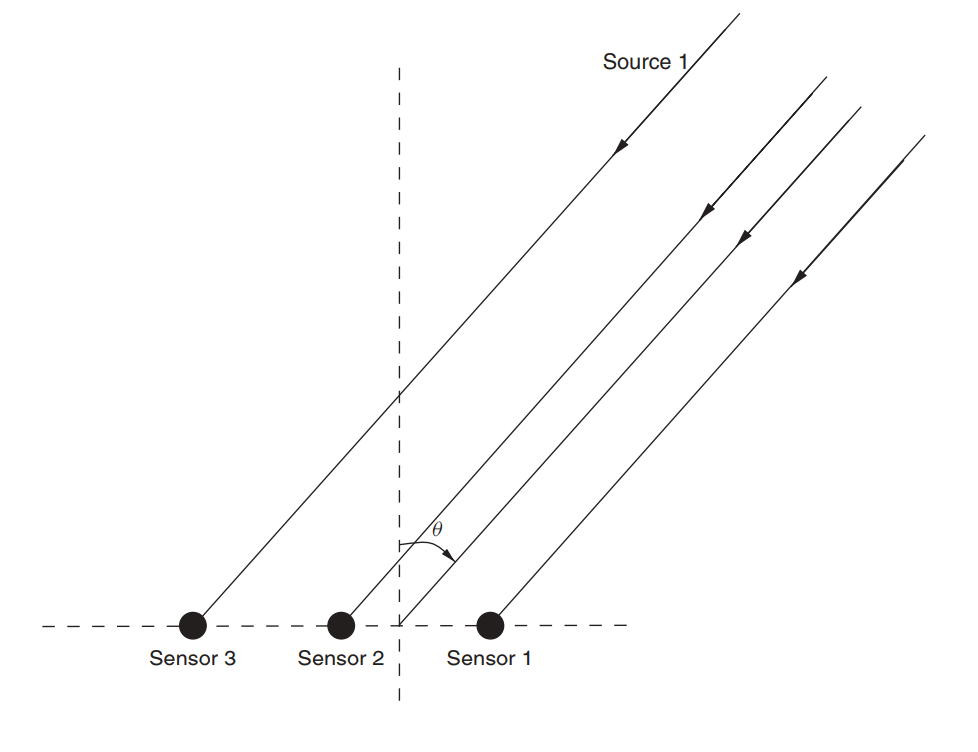
Fig. 3. Array antena linier non-directional (ULAA - array antena linear seragam) [2, hal. 32].

Tentukan parameter kisi awal:

 M = 5 #    (number of sensors)

Dalam tulisan ini, kami akan mempertimbangkan sesuatu seperti saluran broadband dengan fading , fitur karakteristik yang merupakan propagasi multipath . Untuk kasus-kasus seperti itu, suatu pendekatan biasanya diterapkan di mana setiap balok dimodelkan menggunakan penundaan dari besarnya tertentu (Gbr. 4).

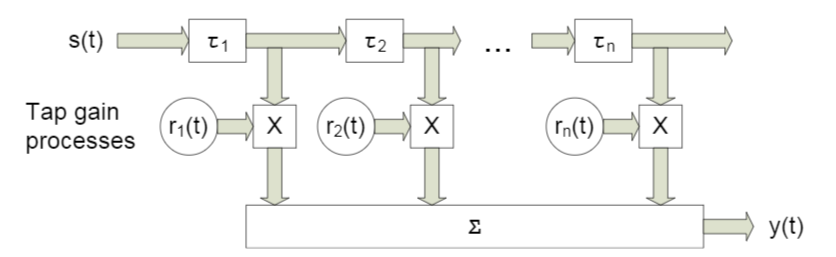
Fig. 4. Model saluran broadband dengan n penundaan tetap. [3, hal. 29]. Seperti yang Anda pahami, sebutan khusus tidak berperan - lebih lanjut kami akan menggunakan yang sedikit berbeda.

Model sinyal yang diterima untuk satu sensor dinyatakan sebagai berikut:

$x (n) = \ sum_ {l = 0} ^ Lh (l) s (n-l) + \ nu (n)$

Dalam hal ini menunjukkan nomor referensi, h (l) Apakah respons saluran sepanjang balok ke- l , L adalah jumlah register penundaan, s adalah sinyal yang ditransmisikan (berguna), $\ nu (n)$ - Kebisingan tambahan.

Untuk beberapa sensor, rumusnya akan berbentuk:

$\ mathbf {x} (n) = \ mathbf {H} \ mathbf {s} (n) + \ mathbf {\ nu} (n)$

dimana $\ mathbf {x} (n)$ dan $\ mathbf {\ nu} (n)$ - Memiliki dimensi $M \ kali 1$ dimensi $\ mathbf {H}$ sama dengan $M \ kali (M-L)$ , dan dimensi $\ mathbf {s} (n)$ sama dengan $(M-L) \ kali 1$ .

Misalkan setiap sensor juga menerima sinyal dengan penundaan tertentu, karena timbulnya gelombang pada suatu sudut. Matriks $\ mathbf {H}$ dalam kasus kami, ini akan menjadi matriks konvolusional untuk vektor respons untuk setiap sinar. Saya pikir kodenya akan lebih jelas:

 h = np.array([0.722-1j*0.779, -0.257-1j*0.722, -0.789-1j*1.862]) L = len(h)-1 # number of signal sources H = convmtx(h,ML) print(H.shape) print(H)

Kesimpulannya adalah:

 >>> (5, 3) >>> array([[ 0.722-0.779j, 0. +0.j , 0. +0.j ], [-0.257-0.722j, 0.722-0.779j, 0. +0.j ], [-0.789-1.862j, -0.257-0.722j, 0.722-0.779j], [ 0. +0.j , -0.789-1.862j, -0.257-0.722j], [ 0. +0.j , 0. +0.j , -0.789-1.862j]])

Selanjutnya, kami mengatur data awal untuk sinyal dan noise yang berguna:

 sigmaS = 1 #    (the signal's s(n) power) sigmaN = 0.01 #   (the noise's n(n) power)

Sekarang kita beralih ke korelasi.

 Rxx = (sigmaS)*(np.dot(H,np.matrix(H).H))+(sigmaN)*np.identity(M) p = (sigmaS)*H[:,0] p = p.reshape((len(p), 1))

Derivasi formula di sini (juga selembar untuk yang paling putus asa).

Kami menemukan solusi untuk Wiener:

 # Solution of the Wiener-Hopf equation: wopt = np.dot(np.linalg.inv(Rxx), p) MSEopt = MSE_calc(sigmaS, Rxx, p, wopt)

Sekarang mari kita beralih ke metode gradient descent.

Temukan nilai eigen terbesar sehingga batas atas langkah dapat diturunkan darinya (lihat rumus (9)):

 lamda_max = max(np.linalg.eigvals(Rxx))

Sekarang mari kita atur beberapa langkah yang akan membuat sebagian kecil dari maksimum:

 coeff = np.array([1, 0.9, 0.5, 0.2, 0.1]) mus = 2/lamda_max*coeff # different step sizes

Tentukan jumlah iterasi maksimum:

 N_steps = 100

Jalankan algoritme:

 MSE = np.empty((len(mus), N_steps), dtype=complex) for mu_idx, mu in enumerate(mus): w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): w = w - mu*(np.dot(Rxx, w) - p) MSE[mu_idx, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Sekarang kita akan melakukan hal yang sama, tetapi untuk langkah adaptif (rumus (10)):

 MSEoptmu = np.empty((1, N_steps), dtype=complex) w = np.zeros((M,1), dtype=complex) for N_i in range(N_steps): gamma = p - np.dot(Rxx,w) mu_opt = mu_opt_calc(gamma, Rxx) w = w - mu_opt*(np.dot(Rxx,w) - p) MSEoptmu[:, N_i] = MSE_calc(sigmaS, Rxx, p, w)

Anda harus mendapatkan sesuatu seperti ini:

Menggambar

 x = [i for i in range(1, N_steps+1)] plt.figure(figsize=(5, 4), dpi=300) for idx, item in enumerate(coeff): if item == 1: item = '' plt.loglog(x, np.abs(MSE[idx, :]),\ label='$\mu = '+str(item)+'\mu_{max}$') plt.loglog(x, np.abs(MSEoptmu[0, :]),\ label='$\mu = \mu_{opt}$') plt.loglog(x, np.abs(MSEopt*np.ones((len(x), 1), dtype=complex)),\ label = 'Wiener solution') plt.grid(True) plt.xlabel('Number of steps') plt.ylabel('Mean-Square Error') plt.title('Steepest descent') plt.legend(loc='best') plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()

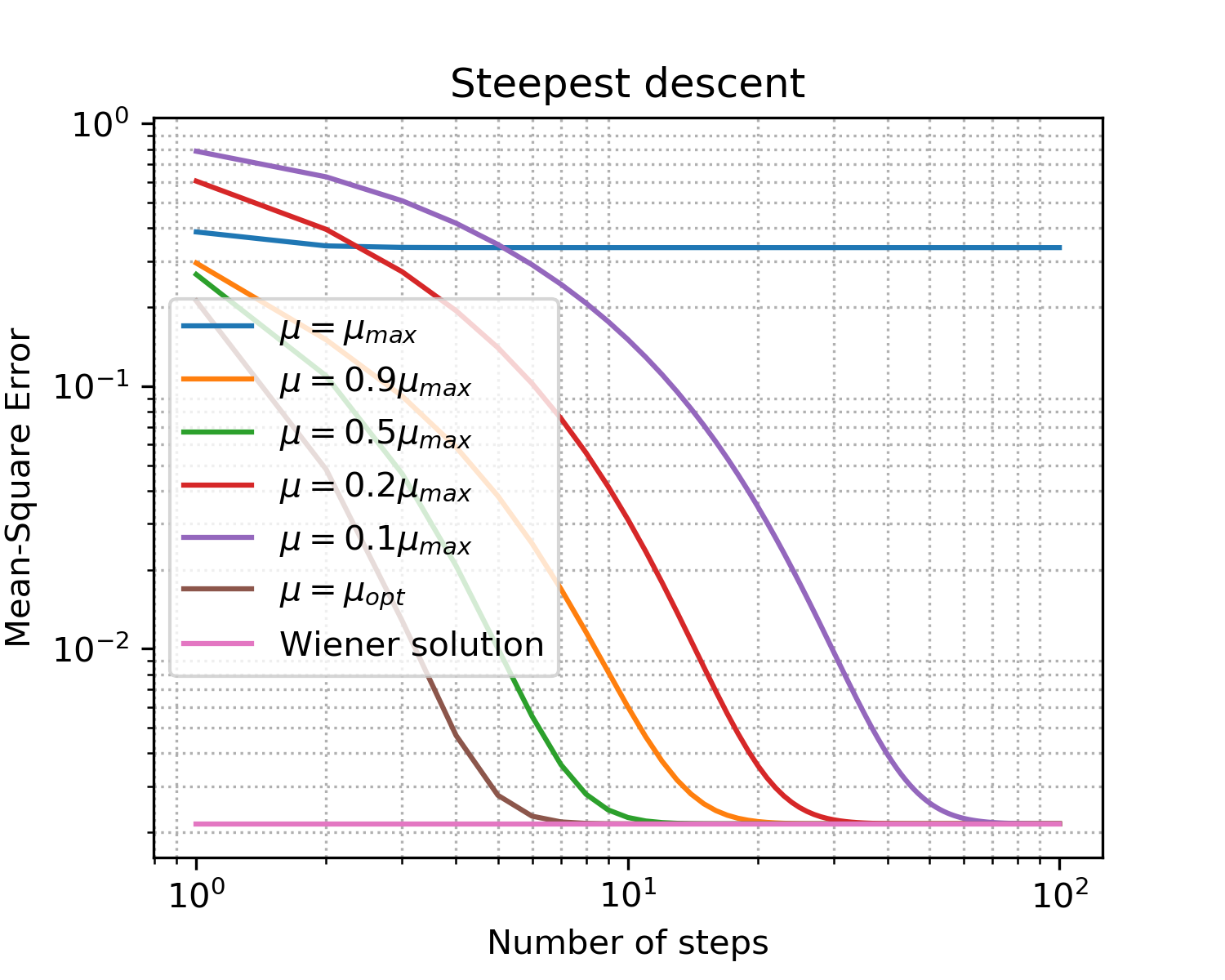
Fig. 5. Kurva belajar untuk langkah-langkah ukuran yang berbeda.

Pengencang demi berbicara poin utama pada gradient descent:

seperti yang diharapkan, langkah optimal memberikan konvergensi tercepat;
tidak lagi berarti lebih baik: setelah melampaui batas atas, kita belum mencapai konvergensi sama sekali.

Jadi kami menemukan vektor optimal dari filter filter yang akan meningkatkan level efek saluran - kami melatih equalizer .

Apakah ada sesuatu yang lebih dekat dengan kenyataan?

Tentu saja! Kami telah mengatakan beberapa kali bahwa mengumpulkan statistik (mis. Menghitung matriks dan vektor korelasi) dalam sistem waktu nyata jauh dari selalu merupakan kemewahan yang terjangkau. Namun, umat manusia telah beradaptasi dengan kesulitan-kesulitan ini: alih-alih pendekatan deterministik dalam praktiknya, pendekatan adaptif digunakan. Mereka dapat dibagi menjadi dua kelompok besar [1, hal. 246]:

probabilistic (stochastic) (mis. SG - Stochastic Gradient)
dan berdasarkan pada metode kuadrat terkecil (misalnya, LMS - Least Mean Square atau RLS - Recursive Least Squares)

Topik filter adaptif terwakili dengan baik dalam komunitas open-source (contoh untuk python):

Dalam contoh kedua, saya terutama menyukai dokumentasi. Namun berhati-hatilah! Ketika saya menguji paket padasip , saya menemui kesulitan dalam menangani bilangan kompleks (secara default, float64 tersirat di sana). Mungkin masalah yang sama mungkin muncul ketika bekerja dengan beberapa implementasi lainnya.

Algoritma, tentu saja, memiliki kelebihan dan kekurangannya sendiri, yang jumlahnya menentukan ruang lingkup algoritma.

Mari kita lihat contoh-contoh berikut: kami akan mempertimbangkan tiga algoritma SG , LMS dan RLS yang telah kami sebutkan (kami akan memodelkan dalam bahasa MATLAB - Saya akui, sudah ada yang kosong, dan menulis ulang semuanya menjadi python keseragaman demi ... well ...).

Penjelasan tentang algoritma LMS dan RLS dapat ditemukan, misalnya, di dock padasip .

Deskripsi SG dapat ditemukan di sini.

Perbedaan utama dari gradient descent adalah gradient variabel:

$\ mathbf {w} [n] = \ mathbf {w} [n-1] + \ mu \ kiri (\ mathbf {\ hat {p}} [n] - \ mathbf {\ hat {R}} _ {xx } [n] \ mathbf {w} [n-1] \ kanan)$

$\ mathbf {\ hat {R}} _ {xx} [n] = \ frac {1} {n} \ kiri ((n-1) \ mathbf {\ hat {R}} _ {xx} [n-1 ] + \ mathbf {x} [n] \ mathbf {x} [n] ^ H \ kanan)$

$\ mathbf {\ hat {p}} [n] = \ frac {1} {n} \ kiri ((n-1) \ mathbf {\ hat {p}} [n-1] + \ mathbf {x} [ n] d [n] ^ * \ benar)$

1) Kasus serupa dengan yang dipertimbangkan di atas.

Sumber (MatLab / Oktaf).

Sumber dapat diunduh di sini .

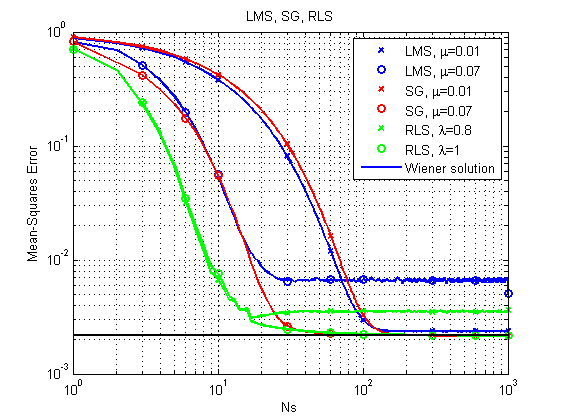
Fig. 6. Kurva belajar untuk LMS, RLS dan SG.

Dapat segera dicatat bahwa dengan kesederhanaan relatifnya, algoritma LMS mungkin, pada prinsipnya, tidak mencapai solusi optimal dengan langkah yang relatif besar. RLS memberikan hasil tercepat, tetapi juga bisa gagal dengan faktor pelepasan yang relatif kecil. Sejauh ini, SG baik-baik saja, tetapi mari kita lihat contoh lain.

2) Kasus saat saluran berubah waktu.

Sumber (MatLab / Oktaf).

Sumber dapat diunduh di sini .

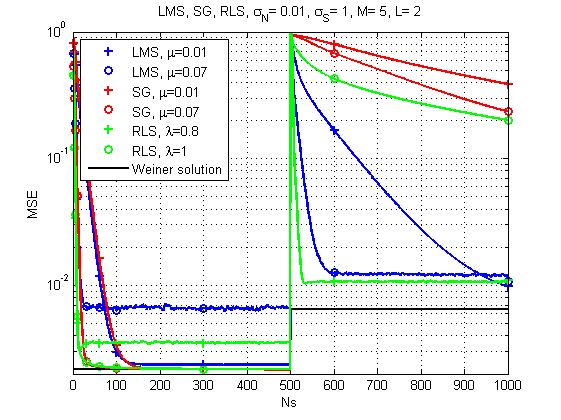
Fig. 7. Kurva belajar untuk LMS, RLS, dan SG (saluran berubah seiring waktu).

Dan di sini gambarnya sudah jauh lebih menarik: dengan perubahan tajam dalam respons saluran, LMS tampaknya menjadi solusi yang paling dapat diandalkan. Siapa sangka. Meskipun RLS dengan faktor lupa yang tepat juga memberikan hasil yang dapat diterima.

Beberapa kata tentang kinerja.

Ya, tentu saja, masing-masing algoritma memiliki kompleksitas komputasi yang spesifik, tetapi menurut pengukuran saya, mesin lama saya dapat mengatasi satu ensemble untuk sekitar 120 μs per iterasi dalam kasus LMS dan SG dan sekitar 250 μs per iterasi dalam kasus RLS. Artinya, perbedaannya, secara umum, sebanding.

Dan itu saja untuk hari ini. Terima kasih untuk semua orang yang melihat!

Sastra

Teori filter Adaptif Haykin SS. - Pearson Education India, 2005.
Haykin, Simon, dan KJ Ray Liu. Buku pegangan tentang pemrosesan array dan jaringan sensor. Vol. 63. John Wiley & Sons, 2010. hlm. 102-107
Arndt, D. (2015). Pemodelan Saluran untuk Penerimaan Satelit Mobile Land (disertasi Doktor).

Lampiran 1

Filter eigen

Tujuan utama filter semacam itu adalah untuk memaksimalkan Signal-to-Noise Ratio (SNR).

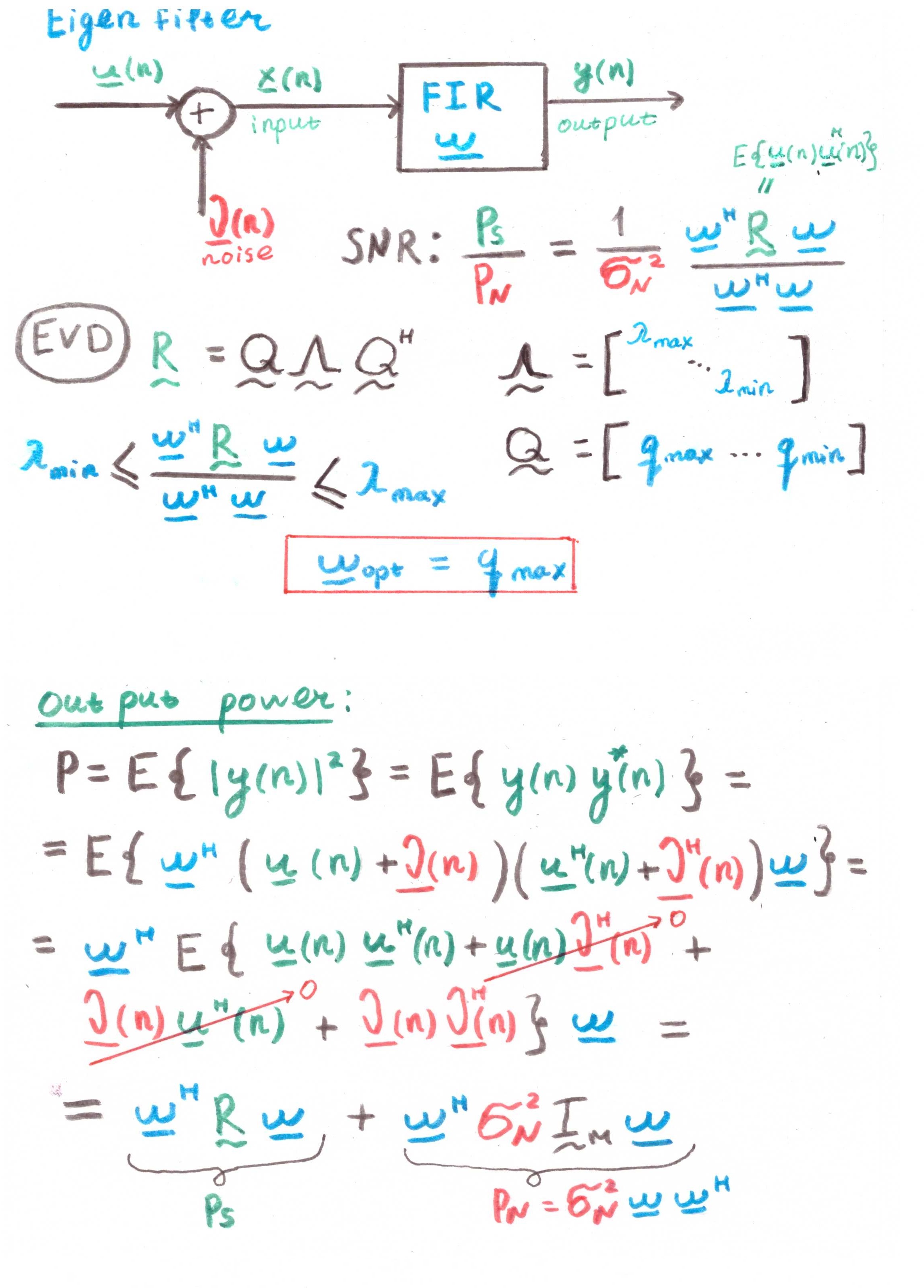
Tetapi dilihat dari adanya korelasi dalam perhitungan, ini juga lebih merupakan konstruksi teoretis daripada solusi praktis.

Penyaringan linear optimal: mulai dari gradient descent hingga filter adaptif