Automata Seluler Berkembang

Hubungkan automata seluler dengan algoritma genetika dan lihat apa yang terjadi.

Artikel ini berisi Gif (traffic!) Dan gambar yang kontras. Epilepsi mungkin memiliki serangan epilepsi.

Aturan untuk automata seluler

Otomat seluler paling sederhana adalah otomat seluler satu dimensi (ada juga automata nol dimensi - kita akan membicarakannya di bawah). Dalam otomat seluler satu dimensi, kita memiliki larik satu dimensi, sel-selnya (sel) dapat mengambil satu dari dua keadaan (1/0, true / false, putih / hitam, hidup / mati). Keadaan sel selanjutnya dalam array ditentukan oleh keadaan sel saat ini dan keadaan dua sel yang berdekatan, menurut beberapa aturan.

Total ada $$$2 ^ 3 = 8$kombinasi keadaan sel dan dua sel tetangga:



Selanjutnya, untuk setiap kombinasi, kami menuliskan status sel untuk iterasi berikutnya (untuk keadaan otomat berikutnya):



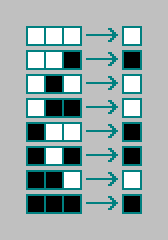
Punya aturan untuk otomat seluler. Aturan untuk automata seluler satu dimensi dikodekan dengan 8 bit ("kode Tungsten"). Total ada $$$2 ^ 8 = 256$automata seluler dasar:



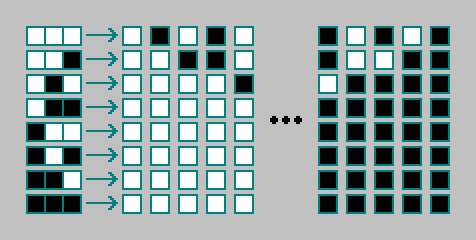
256 mesin dapat disortir secara manual. Kami tidak akan memikirkan mereka. Kami menghitung jumlah aturan yang ada untuk automata seluler dua dimensi.

Automaton seluler dua dimensi menggunakan susunan dua dimensi. Setiap sel memiliki 8 tetangga di sekitar Moore (ada juga lingkungan von Neumann di mana sel-sel diagonal tidak diperhitungkan. Kami tidak akan mempertimbangkannya dalam artikel):



Untuk kenyamanan, kami menulis sel dalam satu baris (kami akan menggunakan urutan yang dipilih nanti dalam artikel):



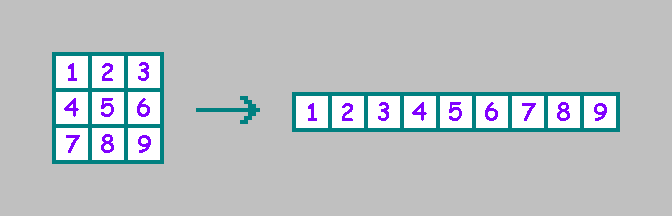
Untuk otomat seluler dua dimensi ada $$$2 ^ 9 = 512$kombinasi keadaan sel dan 8 sel tetangga:



Aturan untuk otomat seluler dua dimensi dikodekan dengan 512 bit. Total ada $$$2 ^ {512}$automata seluler dua dimensi:



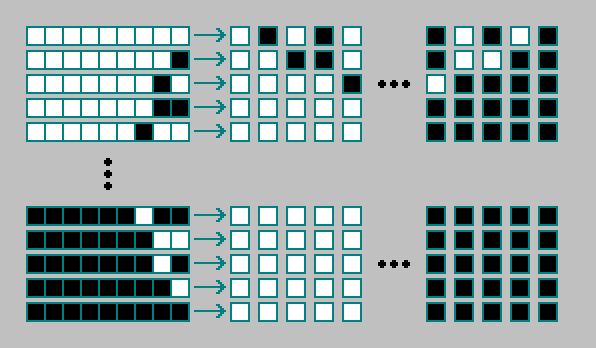
Nomor:

$$

$$2 ^ {512} \ approx1.340781 \ times10 ^ {154}$$

lebih banyak atom di alam semesta yang dapat diamati ( $$$10 ^ {80}$)
Secara manual jumlah mesin ini tidak dapat disortir. Jika kita melihat satu otomat setiap detik - selama keberadaan Semesta, kita akan berhasil melihat semuanya $$$\ approx4.35 \ times10 ^ {17}$mesin otomatis.

Pencacahan sederhana tidak berfungsi, tetapi dengan bantuan algoritma genetika, kita dapat menemukan automata yang paling sesuai dengan kriteria yang telah ditentukan sebelumnya.

Kami akan memprogram dalam JavaScript. Semua fragmen kode disembunyikan di bawah spoiler agar tidak membingungkan pembaca yang tidak terbiasa dengan bahasa pemrograman.

Automaton seluler dua dimensi

Kami menulis otomat seluler dua dimensi dengan aturan acak. Kami akan menyimpan aturan dalam array aturan, yang panjangnya rulesize = 512:


Selanjutnya, isi keadaan awal mesin dengan rumah acak:


(selanjutnya dalam artikel ini, nomor acak diambil sebagai lebar dan tinggi mesin - tidak terlalu besar dan bukan angka ganjil yang sangat kecil 89)

Fungsi yang menghitung keadaan otomat berikut terlihat sebagai berikut (agar tidak membuang sampah sembarangan, itu menghilangkan inisialisasi kanvas):


Variabel xm dan xp menyimpan koordinat X tetangga di sebelah kiri dan tetangga di sebelah kanan (x minus dan x plus). Variabel ym dan yp menyimpan koordinat Y yang sesuai.

Di sini:


kami menetapkan kondisi batas periodik (bidang otomat adalah permukaan torus).

Selanjutnya:


dalam urutan di atas, tulis konten sel ke dalam string. Kami menerjemahkan string ke angka desimal. Untuk kombinasi ini, kami menemukan dalam array aturan menyatakan bahwa sel dengan koordinat x dan y harus diambil.


Setelah semua iterasi, ganti status otomat sebelumnya dengan yang baru:


Kami menggambar automaton menggunakan fungsi setInterval:


Jalankan di browser

Saya sarankan memulai mesin dengan aturan acak 10-20 kali sebelum melanjutkan membaca artikel.

Kita dapat menjalankan mesin untuk waktu yang sangat lama dengan aturan acak yang berbeda. Gambar yang kita dapatkan tidak akan berbeda dari gambar di layar TV tanpa adanya sinyal:



Selanjutnya, mari beralih ke pengaturan "TV" kami menggunakan algoritma genetika.

Algoritma genetika

Ukuran populasi awal adalah 200 mesin (individu). Untuk aturan, alih-alih susunan aturan satu dimensi, kita akan menggunakan susunan populasi dua dimensi. Indeks pertama (n) adalah jumlah individu dalam populasi.


Array kebugaran berisi koefisien kebugaran masing-masing individu. Array ini diisi dalam proses seleksi. Setelah seleksi, kami memulai proses evolusi.

Proses evolusi

Dari populasi kami, kami mengambil setengah dari individu yang paling beradaptasi (sesuai dengan koefisien kebugaran). Setengah sisanya hancur. Selanjutnya, kami mengambil dua individu yang masih hidup dan melintasinya.



Untuk menyeberang, pilih posisi acak dalam genotipe dua leluhur. Sebelum posisi ini, kita mengambil gen dari satu leluhur, setelah posisi ini - dari yang lain. Kami menempatkan gen yang dipilih dalam genotipe ke satu keturunan. Gen yang tersisa adalah untuk yang lain. Kami menempatkan dua leluhur dan dua keturunan dalam populasi baru. Pada saat yang sama, setiap individu berpartisipasi dalam persilangan satu waktu.

Mutasi. Dengan probabilitas 5%, satu gen yang dipilih secara acak bermutasi (membalikkan) pada setiap individu. Jika Anda meningkatkan kemungkinan mutasi, akan ada lebih banyak mutan yang berhasil, tetapi pada saat yang sama, mutan yang berhasil mungkin tidak punya waktu untuk meninggalkan keturunan yang sukses sebelum bermutasi lagi dengan tidak berhasil. Kami akan kembali ke masalah ini nanti.

Seleksi alam

Sebelum memulai proses evolusi, seleksi harus dilakukan. Seleksi dapat bersifat alami dan buatan. Seleksi buatan dibuat secara manual - tentang hal itu nanti. Untuk seleksi alam, kami akan menetapkan beberapa kriteria dan memilih mesin yang paling cocok dengan kriteria yang diberikan.

Kriteria apa yang bisa ditentukan sebelumnya? Ambil yang termudah. "TV" kami terlalu banyak berkedip. Kami menyimpan dua status otomat seluler - pada 99 dan pada 100 iterasi. Hitung jumlah sel yang belum berubah. Angka yang dihasilkan akan digunakan sebagai koefisien kebugaran. Jelas, satu kriteria saja tidak cukup untuk kita. Sangat mudah untuk secara manual memilih automaton yang akan paling memenuhi kriteria yang diberikan: automaton [0,0,0, ..., 0] dan automaton [1,1,1, ..., 1]. Pada iterasi pertama, kedua automata ini diisi dengan nol atau satu dan berhenti mengubah statusnya. Kami mendefinisikan kriteria kedua: perbedaan antara jumlah 0 dan 1 (sel) dalam mesin tidak melebihi 100 (angka tersebut diambil "dari bulldozer").

array1 - keadaan otomat pada iterasi ke-99. array2 - pada iterasi ke-100:


Kita mulai. Solusi optimal ditemukan pada siklus evolusi ke-421. Pada grafik Anda dapat melihat progresnya:



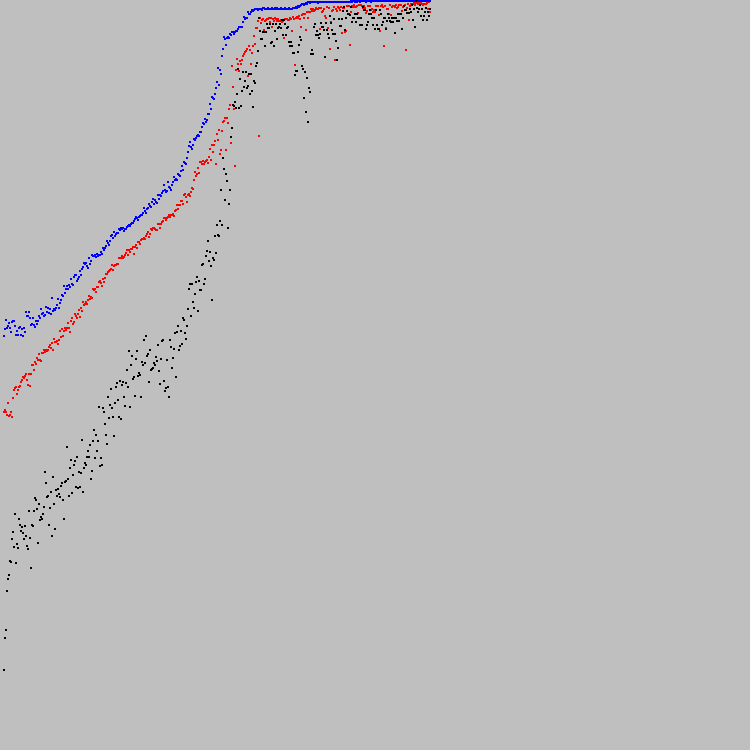
Grafik diskalakan di sepanjang sumbu Y. Titik bawah adalah 0, titik tertinggi adalah 7921. Jelas, 7921 adalah solusi optimal (semua sel dalam mesin 89x89 memenuhi kriteria yang ditentukan). Setelah 100 iterasi, tidak ada sel yang mengubah kondisinya.

Titik-titik biru pada grafik adalah individu terbaik dalam populasi. Merah adalah yang terburuk (hanya individu yang memenuhi kriteria kedua yang diperhitungkan). Titik hitam - koefisien rata-rata kesesuaian untuk seluruh populasi (dengan memperhitungkan individu yang tidak memenuhi kriteria kedua). Kriteria kedua (keseimbangan antara putih dan hitam) sangat sulit. Beberapa automata tidak memenuhi kriteria kedua bahkan setelah 421 siklus evolusi. Oleh karena itu, titik-titik hitam di bawah merah.

Kumpulan gen populasi (individu di sepanjang sumbu Y, gen di sepanjang sumbu X):



Mari kita lihat saluran mana "TV" kami tangkap:



Solusi yang ditemukan bukan satu-satunya yang optimal. Jika kita menjalankan kembali evolusi (dengan genotipe awal acak), kita akan menemukan solusi optimal lainnya. Salah satunya:



Ubah kriteria pemilihan.

Kami akan mempertimbangkan jumlah sel yang pola muncul di sekitar Moore orde 2. Mari kita ambil pola yang paling sederhana:



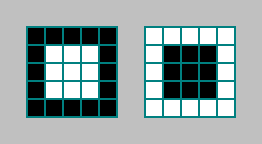
Kriteria ini menarik karena kami memeriksa 25 sel, sedangkan otomaton menghitung keadaan sel berdasarkan keadaan 9 sel.

Kriteria sangat ketat. Jika kita mengambil otomat acak, setelah 100 iterasi akan terlihat seperti ini:



Tidak ada sel tunggal dalam otomat seperti itu yang memenuhi kriteria yang diberikan. Karena itu, kami melunakkan kriteria sedikit:

1. Mari kita membuat satu kesalahan dalam polanya.
2. Kami tidak akan mencari pola pada iterasi terakhir, tetapi pada 50 iterasi terakhir.

Kriteria kedua (keseimbangan antara putih dan hitam) dihapus.

Kita mulai. Bagan:



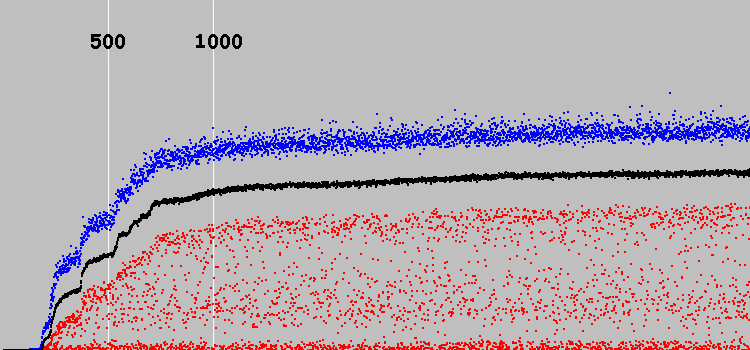
Sumbu y adalah arbitrer. (Di mesin sebelumnya, solusi optimal adalah 7921. Di mesin ini, sekitar 30.)
Sumbu X - 3569 siklus evolusi. Dua garis vertikal putih menandai 500 dan 1000 siklus evolusi.
Titik biru - individu terbaik dalam populasi, merah - terburuk, hitam - rasio rata-rata untuk seluruh populasi.

Solusinya ditemukan dalam 500 siklus pertama evolusi. 500 siklus berikutnya, solusinya membaik. Dan kemudian sistem praktis berhenti berkembang.

Dalam tiga gambar di bawah ini: 500 siklus, 1000 siklus, dan 3569 siklus evolusi:



Gene Pool (3569):



Dalam dinamika:



Pada gambar di bawah ini Anda dapat melihat bagaimana osilator (glider) terbentuk di mesin ini:



Kita dapat memulai mesin dengan keadaan awal di mana satu sel diisi. Selanjutnya, perbaiki semua kombinasi sel yang ditemukan dalam iterasi otomat berikut. Array gen (genotipe otomat) adalah array dari semua kombinasi yang memungkinkan. Setelah mengisolasi hanya kombinasi yang terjadi, kita dapat dengan mudah mencatat semua gen yang terlibat dalam pembentukan osilator. Batang abu-abu adalah gen yang tidak berpartisipasi dalam pembentukan osilator:



Mutasi pada gen ini tidak berakar karena fakta bahwa mereka mengganggu pembentukan pola.

Di mesin kami, sebuah pola (kotak) terbentuk hanya di sekitar sel hitam. Mari kita coba memulai proses evolusi bersama dengan kriteria kedua: perbedaan antara jumlah sel putih dan hitam tidak melebihi 400.

Kami memulai 3569 siklus evolusi. Bagan:



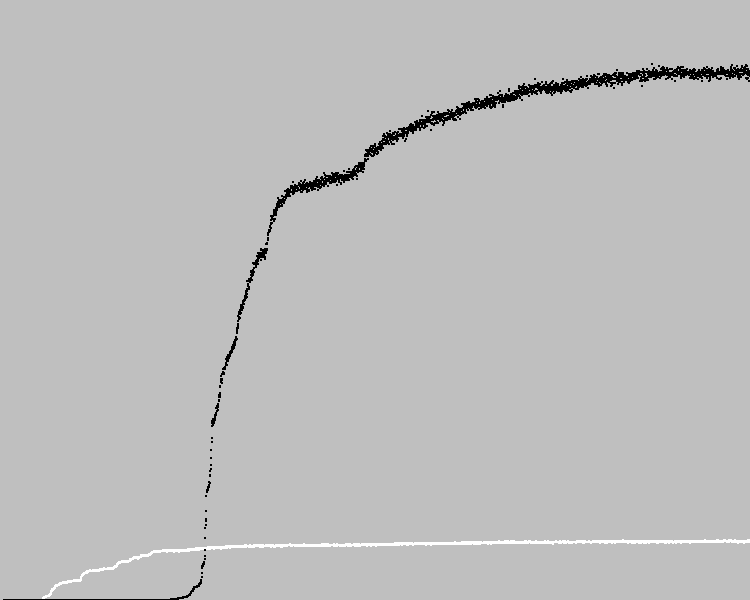
Titik hitam pada grafik adalah koefisien kebugaran rata-rata dalam suatu populasi. Titik putih - koefisien rata-rata kebugaran mesin sebelumnya. Menemukan solusi dengan satu kesalahan dalam polanya.

Kolam gen:



100 iterasi pertama:



Terakhir (100) iterasi:



Sedikit bukan hasil yang kami harapkan. Ada kotak hitam, putih - tidak. Kencangkan kriteria kedua: perbedaan antara jumlah sel putih dan hitam tidak melebihi 100.

Kami memulai 14865 siklus evolusi.
Grafik membandingkan koefisien kebugaran rata-rata populasi. Titik biru adalah senapan mesin kami. Putih dan hitam adalah mesin sebelumnya.



Otomat berevolusi dengan sangat kuat sehingga tampaknya tidak berevolusi sama sekali. Grafik kedua diskalakan sepanjang sumbu Y. Dua garis putih - 500 dan 1000 siklus.



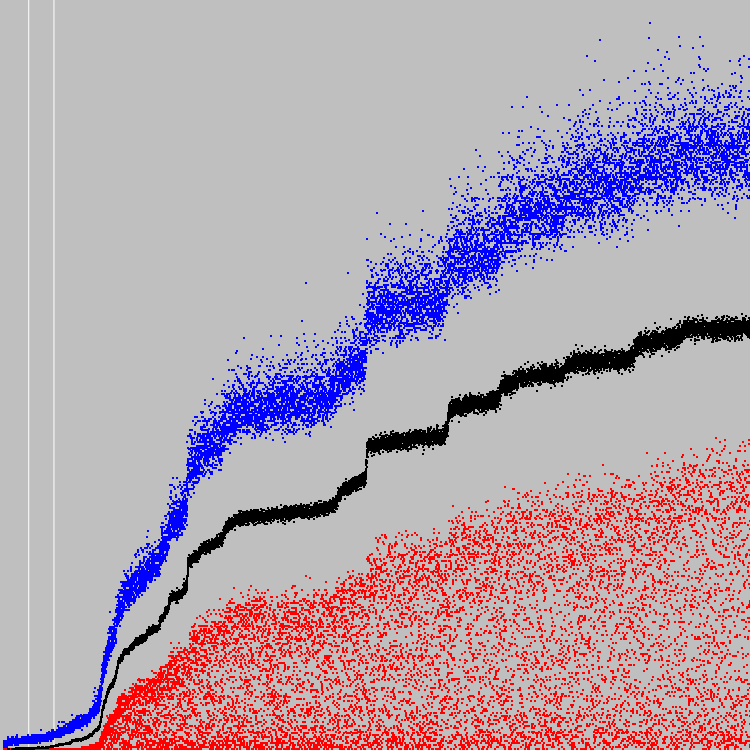
Pada individu terbaik, rata-rata, 6 sel sesuai dengan kriteria yang diberikan.

Mari kita lihat mesin acak dari suatu populasi.
50 iterasi:



Terakhir (50) iterasi:



Tidak ditemukan hasil yang dapat diterima. Kriteria kedua mempersulit pencarian, jadi kami akan menolaknya (kami tidak akan menggunakannya nanti dalam artikel). Mari kita tinggalkan pola ini dan mencari beberapa pola lainnya.

Pola:



Kita mulai. 3000 siklus evolusi. Bagan:



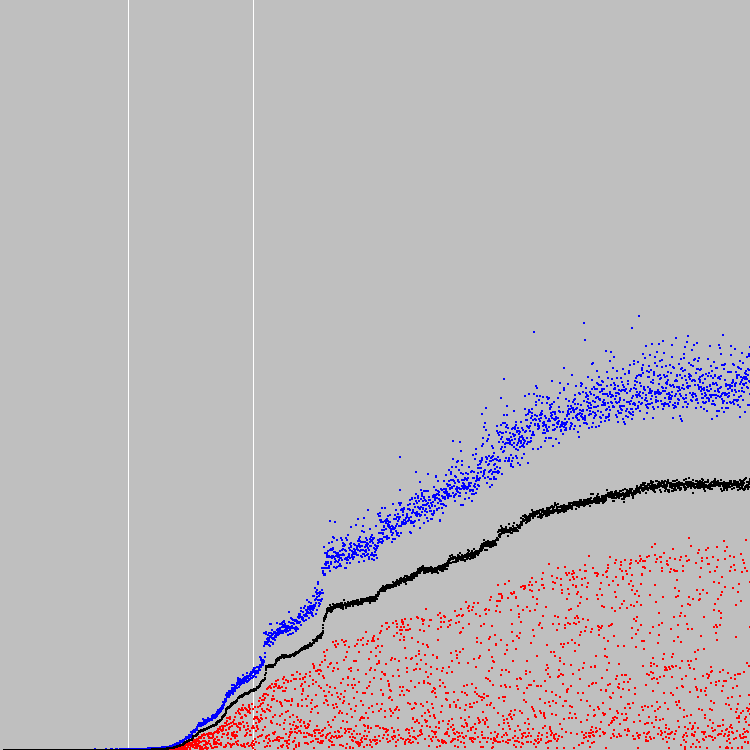
Kolam gen:



Dalam dinamika (100 iterasi):



Terakhir (100) iterasi:



Pola:



Di mesin sebelumnya, kami diizinkan membuat satu kesalahan dalam polanya. Kali ini, mari kita cari pola yang tepat.

Kami memulai 4.549 siklus evolusi. Bagan:



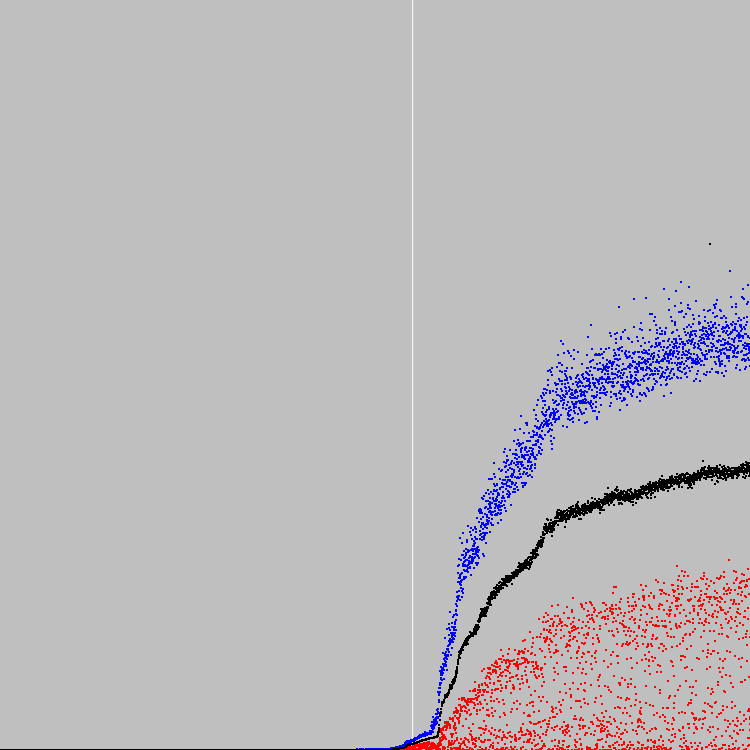
Garis vertikal putih - 2500 siklus evolusi. Pada titik ini (sedikit lebih awal), kebugaran populasi mulai tumbuh dengan cepat. Menyelamatkan populasi untuk melihat solusi sementara. Solusi perantara ternyata jauh lebih menarik daripada solusi pada siklus evolusi ke-4549.

Solusi ditemukan pada siklus evolusi 4549:



Ada 100 iterasi pada Gif. Setelah sejumlah iterasi (sekitar 500-2000), keadaan otomat hampir sepenuhnya dipesan (tinggi dan lebar otomat dipilih secara khusus oleh angka ganjil sehingga otomat tidak dapat sepenuhnya dipesan):



Otomat dengan ukuran sisi yang rata, setelah sejumlah iterasi tertentu, mengambil status yang terurut sepenuhnya. Otomatis 90x90, sekitar 1200 iterasi:



Solusi perantara (ditemukan pada siklus evolusi 2500):



Otomat ini juga dapat memproses keadaan kacau awal tertentu menjadi keadaan terurut terbatas (keadaan terurut akhir adalah pergeseran pola sepanjang sumbu X ke kiri + beberapa sel osilator).

Mesin 16x16 telah disortir dalam sekitar 100 iterasi:



32x32 - sekitar 1000 iterasi:



64x64 - sekitar 6000 iterasi:



90x90 - sekitar 370000 iterasi:



11x11 (dimensi aneh bidang otomat) - sekitar 178700 iterasi:



Senapan serbu 13x13 tidak dipesan dalam jumlah waktu yang dapat diterima.

Pada gambar di bawah ini, mesin pada bidang 256x256 pada iterasi ke-100.000:



Saya sarankan melihat otomat ini dalam dinamika di bidang yang besar - sangat menarik untuk mengamati proses kekacauan swasusun dalam otomat ini: berjalan di browser

Kelompok gen populasi antara:



Memulai kembali proses evolusi memungkinkan Anda menemukan solusi lain. Salah satunya:





Pola lain:



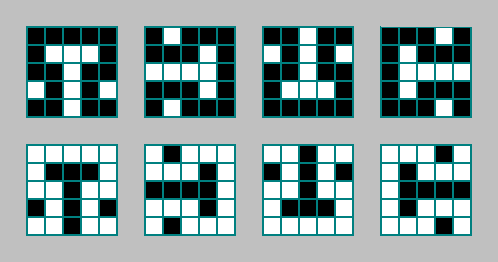
Saat mencari pola, mari kita membuat satu kesalahan lagi (tanpa kesalahan, sistem dengan pola yang dipilih tidak berevolusi).

Kita mulai. 5788 siklus evolusi. Bagan:



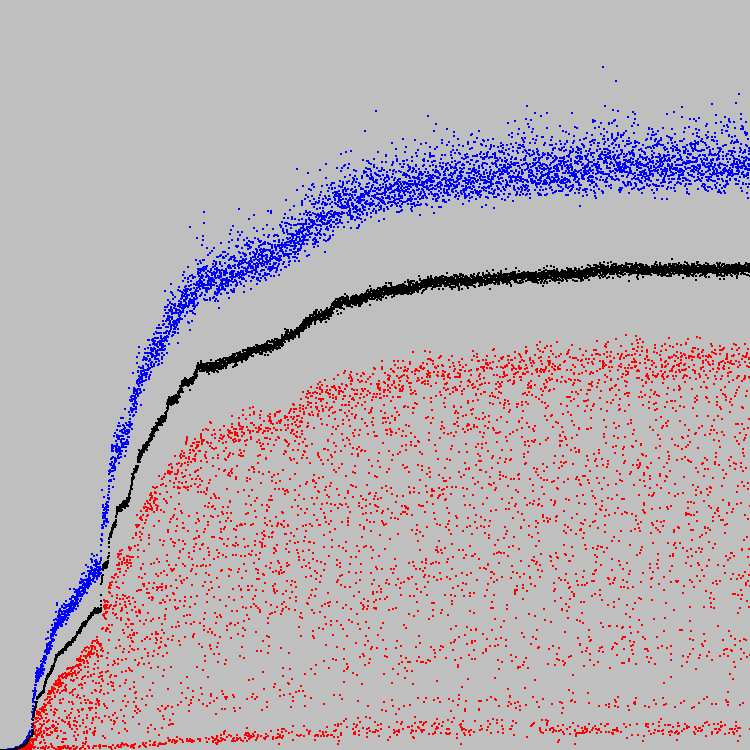
Skala ini arbitrer.

Kolam gen:



Dalam dinamika:



Keadaan otomat (pola bergeser ke atas di sepanjang sumbu Y + beberapa sel osilator):



Jauh lebih menarik untuk mengamati bukan mesin itu sendiri, tetapi mutan yang muncul dalam populasi ini:



Di Gif, mesinnya 256x256. 200 iterasi. Iterasi yang tersisa dapat dilihat di browser .

Seseorang dapat mengakhiri dengan seleksi alam dan beralih ke buatan, tetapi saya ingin menunjukkan berapa banyak $$$2 ^ {512}$sejumlah besar. Di antara jumlah automata ini, kita dapat menemukan otomat yang menggambar setiap pola yang diberikan (dengan akurasi untuk pola yang lebih kompleks).

Pola berikut:



Dalam percobaan sebelumnya, kami menghitung jumlah sel yang membentuk pola (jika dengan satu kesalahan, tambahkan 1 ke jumlah, jika tanpa kesalahan, tambahkan 2). Jumlah yang dihasilkan digunakan sebagai faktor kebugaran untuk algoritma genetika.

Untuk pola yang lebih kompleks, metode ini tidak berfungsi. Otomat di mana jumlah sel yang lebih kecil lebih cocok dengan kriteria yang diberikan (jumlah sel yang cocok dengan pola di sekitar sel) akan setiap kali kalah dari otomat di mana jumlah sel yang lebih besar kurang secara akurat cocok dengan kriteria yang diberikan. Seperti pada contoh dengan kotak di atas:



Untuk pola yang diinginkan, pada iterasi ke-100 setiap otomat dalam populasi, dikelilingi oleh setiap sel, kita akan mempertimbangkan jumlah sel yang cocok dengan pola tersebut. Kami hanya akan mengambil hasil terbaik untuk setiap mesin. Jumlah sel yang cocok dengan pola akan digunakan sebagai faktor kebugaran. Polanya terdiri dari 7x17 = 119 sel. Jumlah ini akan dianggap sebagai solusi optimal. 6000 siklus evolusi memungkinkan kita menemukan otomat yang menggambar pola dengan 5 kesalahan (114 sel bertepatan dengan pola).

Grafik pada skala arbitrer:



Peningkatan persentase mutasi tidak mengganggu kebugaran populasi.

Ada banyak mutan dalam kumpulan gen populasi:



Otomat acak dari populasi dalam dinamika:



Mesin terbaik di iterasi ke-100:



Pola yang dicari dan ditemukan:



Setelah bermain dengan kriteria pemilihan, ukuran bidang otomat dan persentase mutasi, ternyata meningkatkan populasi dan menemukan otomat yang membuat hanya 3 kesalahan dalam pola.

Kolam gen:



Mesin pada iterasi ke-100:



Pola yang dicari dan ditemukan:





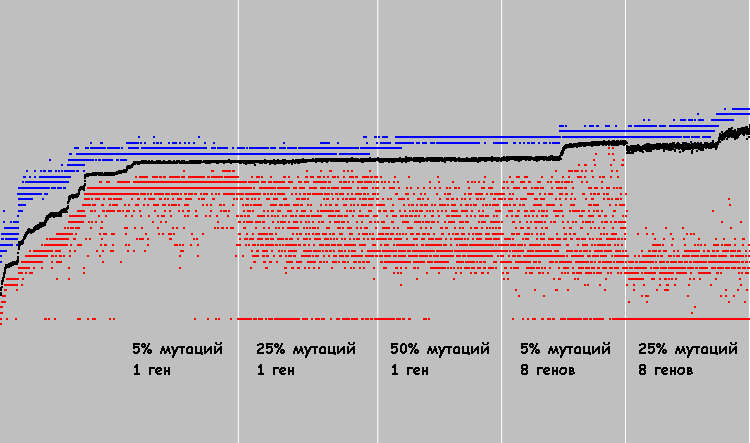
Dalam empat grafik, Anda dapat melihat bagaimana sistem berkembang dengan berbagai probabilitas mutasi (1 mutasi gen):



Titik merah adalah koefisien kebugaran rata-rata dalam suatu populasi. Titik hitam adalah koefisien kebugaran masing-masing individu. 3000 siklus evolusi untuk setiap sistem.

Kelompok gen populasi (dalam urutan yang sama):









Automata pada iterasi ke-100:









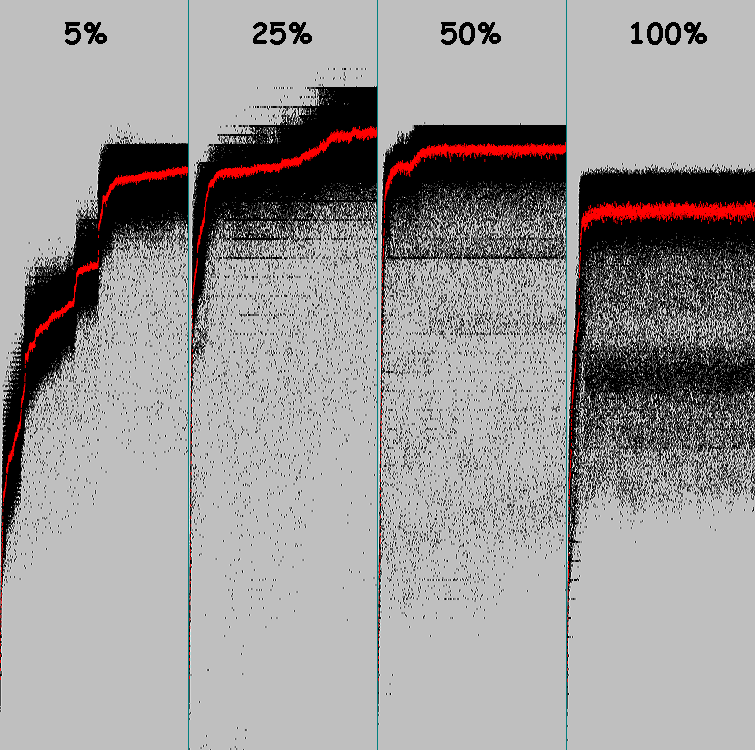
Mari kita lakukan percobaan lain. Polanya sama. Genotipe awal diisi dengan gen acak. Probabilitas mutasi adalah 5%. Dari 1 hingga 8 gen bermutasi (sejumlah acak gen yang bermutasi diambil untuk setiap individu). 100 siklus evolusi.



Grafik adalah peta panas. Ukuran titik pada grafik adalah 5 piksel. Asalnya adalah sudut kiri atas.
Pada sumbu Y (dari 0 hingga 100) - siklus evolusi. Pada sumbu X (dari 0 hingga 119) - jumlah sel bertepatan dengan pola (untuk setiap individu dalam populasi kami mengambil hasil terbaik). Kecerahan titik adalah jumlah individu dengan hasil yang ditentukan (koordinat X).

Jalankan algoritma genetika 4 kali dengan parameter yang sama (100 siklus, 5% mutasi, hingga 8 gen bermutasi). Pada grafik, semua 5 dimulai:



5 dimulai berikut ini: mutasi 25%, hingga 8 gen bermutasi:



Sampelnya kecil, tetapi kita bisa menarik kesimpulan tentang efektivitas peningkatan persentase mutasi.

Selanjutnya, saya akan menunjukkan ketidakefisienan metode penyilangan yang digunakan dalam artikel.

Metode yang Sebelumnya Digunakan:



Alih-alih membagi genotipe menjadi dua bagian, keturunan akan mewarisi gen leluhur acak:



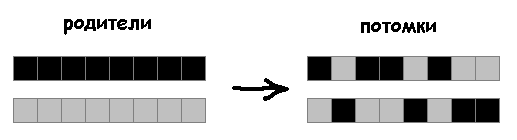
5% mutasi:



25%:



Selanjutnya kita akan menggunakan metode persilangan ini.

Pada ini dengan selesai seleksi alam. Jika seseorang memiliki ide-ide menarik tentang kriteria seleksi alam - silakan sampaikan dalam komentar.

Untuk seleksi buatan, kami akan menggunakan automata seluler tingkat dua .

Otomat seluler orde kedua

Pertimbangkan otomat seluler nol-dimensi dari urutan pertama (semua automata seluler yang kami pertimbangkan di atas adalah urutan pertama). Otomat seluler nol-dimensi terdiri dari satu sel. Sel dapat berada di salah satu dari dua keadaan. Keadaan sel selanjutnya (t) ditentukan oleh keadaan sel saat ini (t-1). Secara total, ada 4 automata seluler nol dimensi (di antaranya satu osilator):



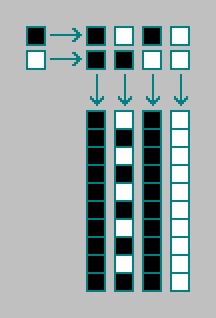
Dalam otomat seluler orde dua, keadaan sel berikutnya (t) ditentukan oleh keadaan saat ini (t-1) dan keadaan sel sebelumnya (t-2). Secara total, ada 4 kombinasi dari dua kondisi sel. $$$2 ^ {4} = $ 1$- Jumlah automata seluler nol-dimensi dari urutan kedua:



Automata seluler semacam itu menunjukkan osilator yang lebih kompleks.

$$$2 ^ {8} = 256$automata seluler dari urutan ketiga:



$$$2 ^ {16} = 65536$automata seluler urutan keempat tidak dapat ditampilkan dalam satu gambar.

Pencarian otomat sel $$$n$urutan ke-2 dengan periode osilasi sama dengan $$$n$- Tugas ini tidak sepele dan sangat menarik. Topik ini layak mendapat artikel terpisah.

Dalam automata seluler satu dimensi dua dimensi, keadaan sel berikut ditentukan oleh keadaan saat ini dari tiga sel dan keadaan sebelumnya dari satu sel:



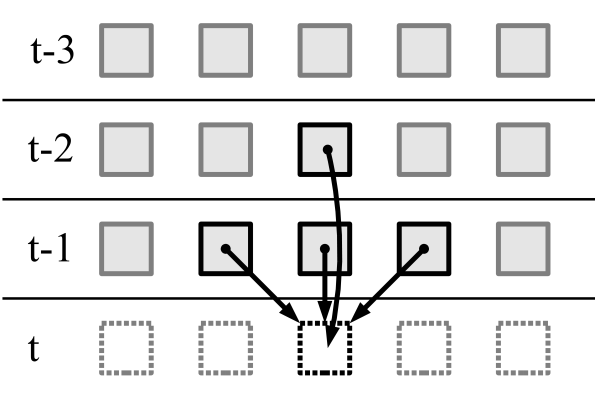
Ada $$$2 ^ {16} = 65536$automata seluler satu dimensi dari orde kedua.

Kode:



, .

, ( — t-1 , — t-1 t-2, — rule):

0011111011001000:


0101101110011110:


0110000110010010:


0110011010010110:


1110011010010110:


0110111010000101:


1111101001110110:


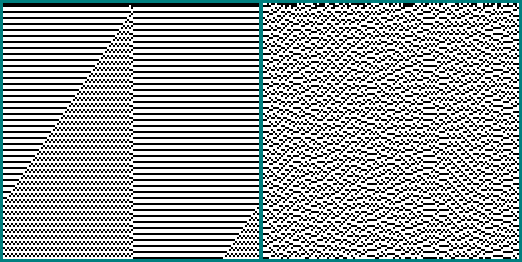
1001010001100000:


256256:



512512



:
.
.

«A New Kind of Science».

, (t-2) .

:



, , :



, $$$2^{512}$.
$$$2^{512} \times 2^{512} = 2^{1024}$

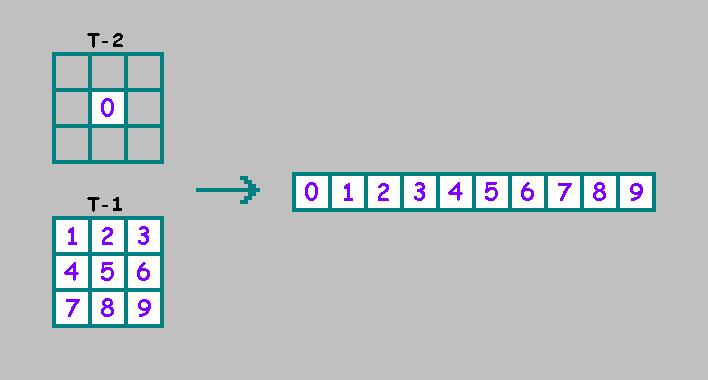
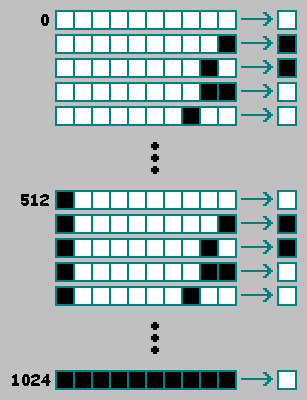
1. Dalam kondisi awal mesin, satu sel diisi

— , .

. (30 ):





, . :





20 ( 30- ):



:



:



, ( ).

2.

Jika rasio unit dan nol dalam genotipe dilanggar, rasio unit dan nol dalam fenotipe dilanggar.

Dalam genotipe (aturan) otomat, kondisi sel berikut dicatat untuk semua kemungkinan kombinasi sel dan sel tetangga. Jika ada lebih banyak nol (atau yang) dalam genotipe, maka nol (atau yang) terakumulasi dalam keadaan otomat berikut. Sangat menarik untuk melihat korelasi antara rasio satu dan nol dalam genotipe dan rasio satu dan nol dalam fenotipe.

Buat grafik.

Buat populasi 200 mesin. Kami mengisi genotipe dengan nol (1024 gen dalam genotipe otomat orde dua dua-dimensi). Selanjutnya$$$n$$$$n=0$$$$n=512$ . Sepanjang sumbu $$$x$$$$y$( ) . :



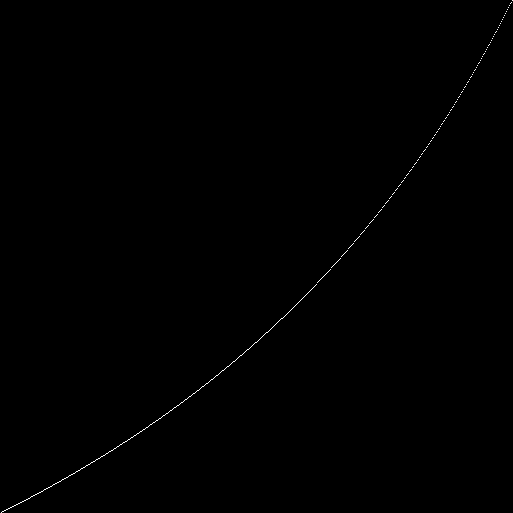
( 8989) 100 . 100- () . ( ). :



, :



. , , . — . . :



, :



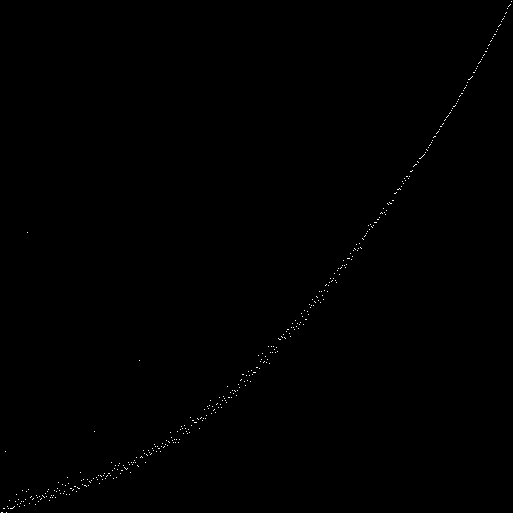
«» — 512-. , .

0- 512- :



0- . 512- :



, 0- 512- .

, , 0- 512- .

8 , 0- ( , — ):



, 512- :



, 0- 512- :



Mari kita pilih tempat pada grafik di mana populasi mulai membaginya menjadi kelompok-kelompok:



Di tempat ini, genotipe diisi 25%.

Bandingkan dua populasi.

Populasi pertama. 30 mesin acak pada iterasi ke-1000. Genotipe 50% penuh (512 unit dan 512 nol):



Populasi kedua. 30 mesin acak pada iterasi ke-1000. Genotipe 25% penuh (256 unit dan 768 nol):



Populasi kedua cocok untuk seleksi buatan. Kami dapat dengan mudah menyorot beberapa tanda di mesin tersebut. Misalnya: "lebih gelap", "kurang semrawut" (automata di mana sel putih dikelompokkan), dll.

Kami memilih "lebih gelap". Probabilitas mutasi adalah 10%, hingga 4 gen bermutasi. Setelah seleksi pertama:



Setelah seleksi kedua:



Otomat yang menarik muncul dalam populasi.

256x256, status mesin pada iterasi ke-1000:



Mesin secara bertahap mengisi populasi.

Setelah pemilihan kedelapan:



Mesin lain yang menarik muncul.

256x256, status otomat pada iterasi ke-1000:



Populasi setelah tiga belas pilihan:



Beberapa automata dari populasi ini. 256x256, iterasi ke-1000 untuk semua orang. Di bawah gambar adalah tautan, dengan mengkliknya, Anda dapat melihat mesin dalam dinamika:


Lihat dalam dinamika.


Lihat dalam dinamika.


Lihat dalam dinamika.


Lihat dalam dinamika.


Lihat dalam dinamika.


Lihat dalam dinamika.


Lihat dalam dinamika.


Lihat dalam dinamika.


Lihat dalam dinamika.


Lihat dalam dinamika.

3. Conway mesin otomatis dan sejenisnya

Otomat seluler dua dimensi paling terkenal dari orde pertama adalah Conway otomaton Game "Life" .

Aturan untuk otomat Conway ditulis sebagai berikut:
Jika ada 3 sel hidup di sekitar sel mati, sel hidup kembali (jika tidak tetap mati).
Jika ada 2 atau 3 sel hidup di sekitar sel hidup, sel itu tetap hidup (kalau tidak mati).
Sel mati adalah 0, sel hidup adalah 1.

Sekitar sel bisa dari 0 hingga 8 sel hidup. Menurut 9 opsi di sekitar yang hidup dan di sekitar sel mati. Kami menulis semua opsi ke r array:



Paruh pertama array adalah untuk sel mati, yang kedua untuk sel hidup.

Kita dapat menulis aturan robot Conway untuk semua kemungkinan (512) kombinasi sel dan 8 sel tetangga:





Untuk otomat urutan kedua, salin bagian kedua dari larik aturan dari yang pertama:



Kami memulai mesin dengan aturan yang ditentukan. Kami melihat glider dan osilator yang khas. Beberapa iterasi otomat ini: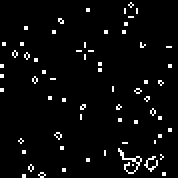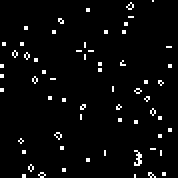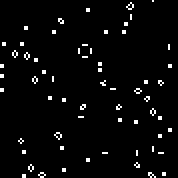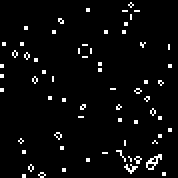



Array r terdiri dari 18 sel. Ada$$$2^{18}=262144$ ( : , , ).
( , «Change rule» r ).

( — r):

110010011001111111


100001100110111110


011111000100101110


010000110000110010


001111010011100111


000111001000000110


000101100010100001


000001111101011111


000001100110111111


Untuk algoritma genetika, sebagai genotipe, Anda dapat menggunakan, sebagai array r ( $$$2^{18}$$$$2^{512}$$$$2^{1024}$

$$$2^{18}$— . , (, ).

rule — , ( , ). . , :




keadaan sel pada iterasi berikutnya adalah sama. Setelah penyeberangan pertama, simetri dalam aturan individu-individu keturunan hancur. Individu leluhur mengumpulkan mutasi yang juga menghancurkan simetri. Pelanggaran simetri pada genotipe menyebabkan pelanggaran simetri pada fenotip.

Orang dapat melihat manifestasi dari simetri ini dalam fenotip jika satu sel diisi pada keadaan awal otomat.

Ayo lakukan percobaan. Untuk mempertahankan simetri, kita akan menggunakan array r sebagai genotipe. 5% mutasi, 1 gen bermutasi. Dalam keadaan awal, satu sel diisi.

30 mesin acak dari populasi awal. Keadaan automata pada iterasi ke-30:



Mari kita coba mengisolasi automata tersebut yang paling lambat berkembang (tumbuh) dari satu sel.







Setelah seleksi pertama, mereka menyingkirkan automata yang tidak berkembang:



Dalam populasi baru ada beberapa automata seperti itu (yang tidak berkembang) - ini adalah keturunan dan mutan yang tidak berhasil.

Selanjutnya, kita akan memilih sebagian besar mesin dengan latar belakang putih (sel yang belum dikembangkan mesin).


Populasi setelah pemilihan kedua:



3 pilihan:



5 pilihan:



8 pilihan:



13 pilihan:



Mesin yang sama pada iterasi ke-60:



21 pilihan. Keadaan automata pada iterasi ke-30:



Keadaan automata pada iterasi ke-60:



34 pilihan. Keadaan automata pada iterasi ke-30:



Keadaan automata pada iterasi ke-60:



Selanjutnya, sistem tidak berevolusi. Tiga automata dari populasi ini (

masing-masing 100 iterasi): [1,0,1,1,1,0,0,1,0,0,1,1,1,0,1,0,1,1,1]


[1 , 0,1,1,1,0,0,1,0,0,0,0,0,0,0,0,0,0,1,1,1]]


[1,0,0,1,1,0,0, 1,1,0,1,0,1,1,1,0,1,1,1]


Sebagai perbandingan, mesin acak:

[1,0,0,1,1,1,0,0,1,1,1,0, 0,1,1,0,0,0,1]]

4. Conway otomaton dan sejenisnya (2)

, () . 4 :



, , .

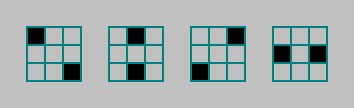
0 2- . 4. $$$3^4=81$. 81- . $$$2^{162}$.

:

$$

$$2^{162}\approx5.846\times10^{48}$$

.

— 162 :


:


rule . fillrule() evolute().

. 30 , 1000- :



, — « ».

:



, . . , .

256256, 10000- . , , :


.


.


.


.


.


.


.


.


.


.


.


.


.


.

?

:

.

:



Start .
Stop — .
One — .
Clear — .
Clear (1 cell) — .
.
(canvas) . 200 — Count 200. Count 5000 — .

20 ( — 200 ). . . Select — (fitness) .
Mutations — .
Gens — .

Start evolution — .

Fill genotype — .
Conway — .

:
.
fenotype.

.

(Local Storage).

( , ) :

4. (2).