Pekerjaan penelitian mungkin merupakan bagian paling menarik dari pelatihan kami. Idenya adalah untuk mencoba diri Anda ke arah yang dipilih bahkan di universitas. Sebagai contoh, siswa dari bidang Rekayasa Perangkat Lunak dan Pembelajaran Mesin sering pergi untuk melakukan penelitian di perusahaan (terutama JetBrains atau Yandex, tetapi tidak hanya).
Dalam posting ini saya akan berbicara tentang proyek saya di bidang Ilmu Komputer. Sebagai bagian dari pekerjaan, saya mempelajari dan mempraktikkan pendekatan untuk memecahkan salah satu masalah NP-hard yang paling terkenal:
vertex meliputi masalah .
Sekarang pendekatan yang menarik untuk masalah yang sulit NP sedang berkembang dengan cepat - algoritma parameter. Saya akan mencoba membuat Anda lebih cepat, memberi tahu beberapa algoritma parameter sederhana dan menjelaskan satu metode ampuh yang banyak membantu saya. Saya mempresentasikan hasil saya di Tantangan PACE: menurut hasil tes terbuka, keputusan saya di tempat ketiga, dan hasil akhir akan diketahui pada 1 Juli.

Tentang diri saya
Nama saya Vasily Alferov, saya sekarang sedang menyelesaikan tahun ketiga HSE - St. Petersburg. Saya telah menyukai algoritma sejak masa sekolah, ketika saya belajar di sekolah Moskow 179 dan berhasil berpartisipasi dalam kompetisi ilmu komputer.
Jumlah akhir spesialis dalam algoritma parameter pergi ke bar ...
Contoh diambil dari buku "Algoritma parameterisasi"Bayangkan bahwa Anda adalah seorang penjaga bar di kota kecil. Setiap hari Jumat, setengah kota datang ke bar Anda untuk bersantai, yang memberi Anda banyak masalah: Anda harus mengusir pengunjung yang kejam dari bar untuk mencegah perkelahian. Pada akhirnya, itu mengganggu Anda dan Anda memutuskan untuk mengambil tindakan pencegahan.
Karena kota Anda kecil, Anda tahu pasti pasangan pengunjung mana yang sangat mungkin bertengkar jika mereka sampai di bar bersama. Anda memiliki daftar
n orang yang akan datang ke bar malam ini. Anda memutuskan untuk tidak membiarkan warga kota masuk ke bar agar tidak ada yang berkelahi. Pada saat yang sama, atasan Anda tidak ingin kehilangan keuntungan dan tidak akan senang jika Anda tidak membiarkan lebih banyak orang pergi ke bar.
Sayangnya, tantangan yang Anda hadapi adalah tugas klasik NP-hard. Anda bisa mengetahuinya sebagai
Vertex Cover , atau sebagai masalah cakupan vertex. Untuk masalah seperti itu, dalam kasus umum, algoritma yang bekerja dalam waktu yang dapat diterima tidak diketahui. Lebih tepatnya, hipotesis ETH yang tidak terbukti dan cukup kuat (Exponential Time Hypothesis) mengatakan bahwa masalah ini tidak dapat diselesaikan pada waktunya.
, yaitu, apa yang terasa lebih baik daripada pencarian lengkap tidak dapat dipikirkan. Sebagai contoh, misalkan
n = 1000 orang berencana untuk datang ke bar Anda. Maka pencarian lengkap akan dilakukan
Pilihan yang ada kira-kira
- Sangat gila. Untungnya, panduan Anda memberi Anda batas
k = 10 , sehingga jumlah kombinasi yang Anda butuhkan untuk beralih lebih sedikit: jumlah himpunan bagian dari sepuluh elemen adalah
. Ini sudah lebih baik, tetapi masih tidak dihitung untuk hari itu, bahkan pada kelompok yang kuat.
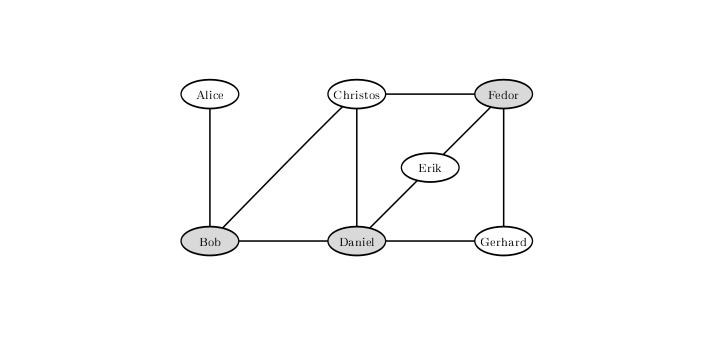
Untuk mengecualikan kemungkinan pertarungan dengan konfigurasi hubungan yang tegang antara pengunjung ke bar, Anda tidak boleh membiarkan Bob, Daniel dan Fedor. Solusi di mana hanya dua yang tersisa tidak ada.
Apakah ini berarti saatnya untuk menyerah dan membiarkan semua orang masuk? Mari kita pertimbangkan opsi lain. Yah, misalnya, Anda tidak bisa membiarkan hanya mereka yang cenderung bertarung dengan jumlah orang yang sangat besar. Jika seseorang dapat bertarung setidaknya dengan
k + 1 oleh orang lain, maka Anda pasti tidak bisa membiarkannya masuk, jika tidak, Anda harus menjauhkan semua warga negara
k + 1 dari siapa yang dapat Anda lawan, yang pasti akan mengecewakan kepemimpinan.
Semoga Anda membuang semua yang Anda bisa sesuai dengan prinsip ini. Maka semua orang bisa bertarung dengan tidak lebih dari
k orang. Mengusir orang-orang dari mereka, Anda dapat mencegah tidak lebih dari
konflik. Jadi, jika semuanya lebih dari
jika seseorang terlibat dalam setidaknya satu konflik, maka Anda tentu tidak dapat mencegah semuanya. Karena, tentu saja, Anda yakin untuk membiarkan orang yang benar-benar tidak berkonflik pergi, maka Anda perlu memilah semua subset ukuran sepuluh dari dua ratus orang. Ada kira-kira
, dan begitu banyak operasi sudah dapat diselesaikan di cluster.
Jika aman untuk mengambil kepribadian yang sama sekali tidak bertentangan, bagaimana dengan mereka yang hanya terlibat dalam satu konflik? Bahkan, mereka juga bisa dibiarkan masuk dengan menutup pintu di depan lawan mereka. Memang, jika Alice hanya konflik dengan Bob, maka jika kita membiarkan dua dari mereka, Alice, kita tidak akan kalah: Bob mungkin memiliki konflik lain, tetapi Alice jelas tidak. Selain itu, tidak masuk akal bagi kita untuk tidak membiarkan keduanya. Setelah operasi seperti itu, tidak ada lagi
tamu dengan nasib yang belum terselesaikan: semua yang kita miliki
konflik, di masing-masing dari dua peserta dan masing-masing terlibat dalam setidaknya dua. Jadi, tinggal memilah saja
pilihan, yang mungkin dihitung selama setengah hari di laptop.
Faktanya, penalaran sederhana dapat mencapai kondisi yang lebih menarik. Perhatikan bahwa kita pasti perlu menyelesaikan semua perselisihan, yaitu, dari setiap pasangan yang bertikai untuk memilih setidaknya satu orang yang tidak akan kita biarkan masuk. Pertimbangkan algoritme ini: ambil konflik apa pun yang kami hapus dari satu peserta dan mulai secara rekursif dari yang lainnya, lalu hapus yang lain dan juga mulai secara rekursif. Karena kita melempar seseorang pada setiap langkah, pohon rekursi dari algoritma semacam itu adalah pohon biner dengan kedalaman
k , oleh karena itu, secara total, algoritma bekerja untuk
di mana
n adalah jumlah simpul dan
m adalah jumlah tepi. Dalam contoh kita, ini adalah sekitar sepuluh juta, yang dalam sepersekian detik akan dihitung tidak hanya pada laptop, tetapi bahkan pada ponsel.
Contoh di atas adalah contoh
algoritma parameter . Algoritma parametrized adalah algoritma yang bekerja selama
f (k) poli (n) , di mana
p adalah polinomial,
f adalah fungsi yang dapat dihitung secara arbitrer, dan
k adalah beberapa parameter yang, sangat mungkin, akan jauh lebih kecil dari ukuran masalah.
Semua diskusi sebelum algoritma ini memberikan contoh
kernelisasi , salah satu teknik umum untuk membuat algoritma parameter. Kernelisasi adalah pengurangan dalam ukuran tugas ke nilai yang dibatasi oleh fungsi parameter. Tugas yang dihasilkan sering disebut kernel. Jadi, dengan alasan sederhana tentang derajat simpul, kami mendapat kernel kuadrat untuk masalah Vertex Cover, yang diparameterisasi oleh ukuran jawabannya. Ada parameter lain yang dapat dipilih untuk tugas ini (misalnya, Vertex Cover Above LP), tetapi kami hanya akan membahas parameter tersebut.
Laju tantangan
Kompetisi
PACE Tantangan (Algoritma Parameter dan Tantangan Eksperimen Komputasi) dimulai pada tahun 2015 untuk membangun koneksi antara algoritma parameter dan pendekatan yang digunakan dalam praktik untuk memecahkan masalah komputasi. Tiga kompetisi pertama dikhususkan untuk menemukan lebar pohon grafik (
Treewidth ), menemukan
Steiner Tree (
Steiner Tree ) dan menemukan banyak simpul, siklus pemotongan (
Feedback Vertex Set ). Tahun ini, salah satu tugas di mana seseorang dapat mencoba kekuatannya adalah masalah penutup atas yang dijelaskan di atas.
Persaingan semakin populer setiap tahun. Jika Anda meyakini data awal, maka tahun ini hanya 24 tim yang ikut serta dalam kompetisi untuk menyelesaikan masalah cakupan verteks. Perlu dicatat bahwa kompetisi tidak berlangsung beberapa jam, dan bahkan tidak seminggu, tetapi beberapa bulan. Tim memiliki kesempatan untuk mempelajari literatur, menghasilkan ide asli mereka dan mencoba menerapkannya. Padahal, kompetisi ini adalah karya penelitian. Gagasan untuk solusi paling efektif dan pemberian pemenang akan diadakan bersamaan dengan konferensi
IPEC (Simposium Internasional tentang Parameterisasi dan Komputasi Tepat) pada pertemuan algoritme tahunan terbesar di
ALGO Eropa. Informasi lebih lanjut tentang kompetisi itu sendiri dapat ditemukan di
situs web , dan hasil beberapa tahun terakhir ada di
sini .
Skema solusi
Untuk mengatasi masalah cakupan verteks, saya mencoba menerapkan algoritma parameter. Mereka biasanya terdiri dari dua bagian: aturan penyederhanaan (yang idealnya mengarah ke kernelisasi) dan aturan pemisahan. Aturan penyederhanaan adalah input preprocessing dalam waktu polinomial. Tujuan penerapan aturan tersebut adalah untuk mengurangi masalah menjadi masalah yang setara dengan ukuran yang lebih kecil. Aturan penyederhanaan adalah bagian paling mahal dari algoritma, dan penerapan bagian khusus ini mengarah pada total waktu kerja
bukannya waktu polinomial sederhana. Dalam kasus kami, aturan pemisahan didasarkan pada fakta bahwa untuk setiap simpul Anda perlu menanggapi salah satu tetangganya.
Skema umumnya adalah ini: kita menerapkan aturan penyederhanaan, lalu memilih beberapa titik, dan membuat dua panggilan rekursif: pertama kita menjawabnya, dan yang lain kita menerima semua tetangganya. Inilah yang kami sebut pemisahan (brunching) di sepanjang puncak ini.
Tepat satu tambahan akan dibuat untuk skema ini di paragraf berikutnya.
Gagasan untuk membagi aturan
Mari kita bahas bagaimana memilih titik di mana pemisahan akan terjadi.
Gagasan utama sangat serakah dalam arti algoritmik: mari kita ambil puncak tingkat maksimum dan membaginya dengan itu. Mengapa ini tampak lebih baik? Karena di cabang kedua dari panggilan rekursif, kami akan menghapus begitu banyak simpul dengan cara ini. Anda dapat berharap bahwa grafik kecil akan tetap dan kami akan bekerja dengan cepat.
Pendekatan ini, dengan teknik-teknik kernelisasi sederhana yang telah dibahas, tidaklah buruk, ia menyelesaikan beberapa tes dengan ukuran beberapa ribu simpul. Tapi, misalnya, itu tidak berfungsi dengan baik untuk grafik kubik (yaitu, grafik yang derajat setiap simpulnya tiga).
Ada ide lain yang didasarkan pada ide yang cukup sederhana: jika grafik terputus, masalah pada komponen yang terhubung dapat diselesaikan secara independen dengan menggabungkan jawaban di akhir. Ngomong-ngomong, ini adalah modifikasi kecil yang dijanjikan dalam skema, yang akan mempercepat solusi secara signifikan: sebelumnya dalam hal ini kami bekerja untuk produk pada saat menghitung tanggapan komponen, dan sekarang kami bekerja untuk jumlahnya. Dan untuk mempercepat proses brunching, Anda perlu mengubah grafik yang terhubung menjadi grafik yang terputus.
Bagaimana cara melakukannya? Jika ada titik artikulasi dalam grafik, perlu untuk mengembara sepanjang itu. Titik artikulasi adalah simpul sedemikian rupa sehingga, ketika dihilangkan, grafik kehilangan konektivitas. Temukan dalam grafik semua titik sambungan dapat berupa algoritma klasik dalam waktu linier. Pendekatan ini secara signifikan mempercepat brunching.
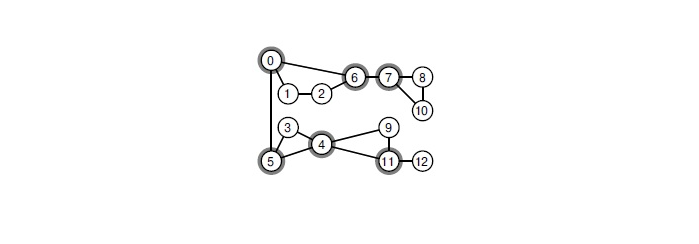
Ketika Anda menghapus salah satu dari simpul yang dipilih, grafik terurai menjadi komponen yang terhubung.
Kami akan melakukannya, tetapi saya ingin lebih. Misalnya, cari bagian vertex kecil di grafik dan pisahkan sepanjang simpul dari itu. Cara paling efektif yang saya tahu untuk menemukan bagian global vertex minimum adalah dengan menggunakan pohon Gomori-Hu, yang dibangun dalam waktu kubik. Dalam Tantangan PACE, ukuran grafik tipikal adalah beberapa ribu simpul. Dalam skenario ini, miliaran operasi perlu dilakukan di setiap sudut pohon rekursi. Ternyata tidak mungkin menyelesaikan masalah dalam waktu yang ditentukan.
Mari kita coba optimalkan solusinya. Bagian simpul minimum antara sepasang simpul dapat ditemukan oleh algoritma apa pun yang membangun aliran maksimum. Anda dapat menjalankan
algoritma Dinitz ke jaringan seperti itu, dalam praktiknya, ia bekerja sangat cepat. Saya memiliki kecurigaan bahwa secara teoritis dimungkinkan untuk membuktikan perkiraan untuk saat bekerja
itu sudah cukup diterima.
Saya mencoba beberapa kali untuk mencari potongan di antara pasangan simpul acak dan mengambil yang paling seimbang dari mereka. Sayangnya, dalam tes PACE Challenge terbuka ini memberikan hasil yang buruk. Saya membandingkannya dengan algoritma yang tersebar di sepanjang simpul dari tingkat maksimum, mulai dengan batasan pada kedalaman keturunan. Setelah algoritma berusaha menemukan potongan dengan cara ini, tetap ada grafik yang lebih besar. Hal ini disebabkan oleh fakta bahwa pemotongan ternyata sangat tidak seimbang: setelah menghilangkan 5-10 puncak, hanya 15-20 yang dapat dipisahkan.
Perlu dicatat bahwa artikel tentang secara teoritis algoritma tercepat menggunakan teknik yang jauh lebih maju untuk memilih simpul untuk dibelah. Teknik-teknik tersebut memiliki implementasi yang sangat kompleks dan seringkali memiliki nilai waktu dan memori yang buruk. Saya tidak dapat membedakan dari mereka cukup dapat diterima untuk latihan.
Cara menerapkan aturan penyederhanaan
Kami sudah punya ide untuk kernelisasi. Biarkan saya mengingatkan Anda:
- Jika ada simpul yang terisolasi, hapus.
- Jika ada simpul derajat 1, hapus dan ambil tanggapan tetangganya.
- Jika ada titik derajat setidaknya k + 1 , terima sebagai tanggapan.
Dengan dua yang pertama semuanya jelas, dengan yang ketiga ada satu trik. Jika dalam masalah bar komik kami diberi batasan dari atas pada
k , maka dalam Tantangan PACE Anda hanya perlu menemukan penutup simpul ukuran minimum. Ini adalah transformasi khas Masalah Pencarian menjadi Masalah Keputusan, seringkali antara dua jenis tugas yang tidak membuat perbedaan. Dalam praktiknya, jika kita menulis pemecah masalah cakupan verteks, mungkin ada perbedaan. Misalnya, seperti pada paragraf ketiga.
Dalam hal implementasi, ada dua cara untuk melakukan ini. Pendekatan pertama disebut Pendalaman Iteratif. Itu terdiri dari yang berikut ini: kita bisa mulai dengan beberapa batasan yang masuk akal dari bawah pada jawabannya, dan kemudian menjalankan algoritma kami, menggunakan batasan ini sebagai batasan pada jawaban dari atas, tanpa turun dalam rekursi yang lebih rendah dari batasan ini. Jika kami menemukan beberapa jawaban, itu dijamin akan optimal, jika tidak, Anda dapat meningkatkan batas ini dengan satu dan mulai lagi.
Pendekatan lain adalah menyimpan beberapa jawaban optimal saat ini dan mencari jawaban yang lebih kecil, ketika ditemukan, ubah parameter ini
k untuk memotong lebih banyak cabang dalam pencarian.
Setelah melakukan beberapa percobaan malam, saya memutuskan kombinasi dari dua metode ini: pertama saya menjalankan algoritma saya dengan beberapa jenis pembatasan pada kedalaman pencarian (memilihnya sehingga membutuhkan waktu yang tidak signifikan dibandingkan dengan solusi utama) dan menggunakan solusi terbaik yang ditemukan sebagai batasan dari atas untuk jawaban - yaitu, untuk itu sangat
k .
Simpul derajat 2
Dengan simpul derajat 0 dan 1 kami menemukan. Ternyata ini juga dapat dilakukan dengan simpul derajat 2, tetapi untuk ini, grafik akan membutuhkan operasi yang lebih kompleks.
Untuk menjelaskan ini, Anda perlu mengidentifikasi puncaknya. Kami menyebut simpul derajat 2 sebagai simpul
v , dan tetangganya adalah simpul
x dan
y . Maka kita akan memiliki dua kasus.
- Ketika x dan y adalah tetangga. Kemudian Anda dapat menerima respons x dan y , dan menghapus v . Memang, setidaknya dua simpul harus diambil dari segitiga ini sebagai respons dan kita tentu tidak akan kalah jika kita mengambil x dan y : mereka mungkin memiliki lebih banyak tetangga, tetapi v tidak.
- Ketika x dan y bukan tetangga. Kemudian dinyatakan bahwa ketiga simpul dapat direkatkan menjadi satu. Idenya adalah bahwa dalam hal ini ada jawaban optimal di mana kita mengambil v atau kedua simpul x dan y . Selain itu, dalam kasus pertama kita harus menanggapi semua tetangga x dan y , dan yang kedua tidak perlu. Inilah yang terjadi ketika kita tidak mengambil titik terpaku sebagai respons dan ketika kita mengambilnya. Tetap hanya untuk mencatat bahwa dalam kedua kasus, respons dari operasi semacam itu berkurang satu.
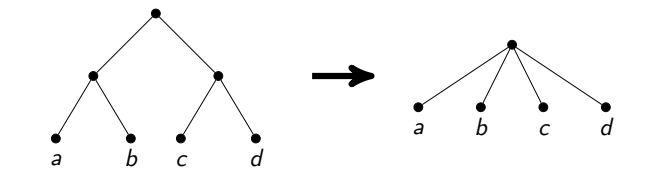
Perlu dicatat bahwa pendekatan seperti itu untuk waktu linear yang jujur cukup sulit untuk diterapkan secara akurat. Merekatkan simpul adalah operasi yang sulit, Anda perlu menyalin daftar tetangga. Jika Anda melakukannya dengan sembarangan, Anda bisa mendapatkan waktu operasi yang tidak optimal secara asimptotik (misalnya, jika Anda menyalin banyak sisi setelah setiap perekatan). Saya memutuskan untuk mencari seluruh jalur dari simpul derajat 2 dan menguraikan banyak kasus khusus, seperti loop dari simpul tersebut atau dari semua simpul tersebut kecuali satu.
Selain itu, perlu bahwa operasi ini dapat dibalik, sehingga selama pengembalian dari rekursi kami mengembalikan grafik dalam bentuk aslinya. Untuk memastikan ini, saya tidak menghapus daftar tepi dari simpul yang digabungkan, setelah itu saya hanya tahu di mana tepi harus diarahkan. Implementasi grafik ini juga membutuhkan akurasi, tetapi menyediakan waktu linear yang jujur. Dan untuk grafik beberapa puluh ribu ujung, itu sepenuhnya cocok dengan cache prosesor, yang memberikan keuntungan kecepatan yang luar biasa.
Inti linier
Akhirnya, bagian paling menarik dari kernel.
Pertama, ingat bahwa dalam grafik bipartit, cakupan verteks minimum dapat dicari
. Untuk melakukan ini, gunakan algoritma
Hopcroft-Karp untuk menemukan pencocokan maksimum di sana, dan kemudian gunakan teorema
Koenig-Egerwari .
Gagasan kernel linear adalah sebagai berikut: pertama kita membagi grafik, yaitu, bukan masing-masing simpul
v, kita mendapatkan dua simpul
dan
, dan bukannya setiap tepi
u - v kita memiliki dua sisi
dan
. Grafik yang dihasilkan akan menjadi bipartit. Kami menemukan di dalamnya cakupan vertex minimum. Beberapa simpul dari grafik asli sampai di sana dua kali, beberapa hanya sekali, dan beberapa tidak pernah sekali. Teorema Nemhauser-Trotter menyatakan bahwa dalam kasus ini adalah mungkin untuk menghapus simpul yang belum mengenai sekali dan untuk menjawab mereka yang memukul dua kali. Selain itu, dia mengatakan bahwa dari puncak yang tersisa (yang mencapai sekali) Anda harus mengambil setidaknya setengah kembali.
Kami baru belajar untuk meninggalkan tidak lebih dari
2k simpul dalam grafik. Memang, jika sisa jawabannya setidaknya setengah dari semua simpul, maka total simpul tidak lebih dari
2k .
Di sini saya berhasil mengambil langkah kecil ke depan. Jelas bahwa kernel yang dibangun dengan cara ini tergantung pada apa jenis cakupan vertex minimum dalam grafik bipartit yang kami ambil. Saya ingin mengambil jumlah simpul yang tersisa minimal. Sebelumnya, mereka hanya tahu cara melakukannya tepat waktu.
. Saya datang dengan implementasi algoritma ini pada waktunya
Dengan demikian, inti ini dapat dicari pada grafik ratusan ribu simpul pada setiap tahap percabangan.
Hasil
Praktek menunjukkan bahwa solusi saya bekerja dengan baik pada tes beberapa ratus simpul dan beberapa ribu tepi. Pada tes semacam itu, dapat diperkirakan bahwa solusinya dapat ditemukan dalam setengah jam. Probabilitas menemukan jawaban dalam periode waktu yang dapat diterima meningkat pada prinsipnya jika grafik memiliki banyak simpul dalam derajat yang besar, misalnya, derajat 10 ke atas.
Untuk berpartisipasi dalam kompetisi, keputusan harus dikirim ke
optil.io . Dilihat dari
piring yang disajikan di sana, keputusan saya untuk tes terbuka menempati urutan ketiga dari dua puluh dengan margin yang lebar dari yang kedua. Sejujurnya, tidak sepenuhnya jelas bagaimana keputusan akan dievaluasi di kompetisi itu sendiri: misalnya, keputusan saya melewati lebih sedikit tes daripada keputusan di tempat keempat, tetapi itu bekerja lebih cepat bagi mereka yang lulus.
Hasil pada tes tertutup akan diumumkan pada 1 Juli.